INS 量测更新
5 量测更新
5.1 GNSS位置及速度更新
r ^ G P S , i n = r ^ I M U n + D R − 1 C b n l b v ^ G P S , i n = v ^ I M U n + ω i n n × C b n l b − C b n ω i b b × l b \begin{aligned} \hat{r}_{GPS,i}^{n} &= \hat{r}_{IMU}^{n} + D_{R}^{-1}C_{b}^{n} l^b\\ \hat{v}_{GPS,i}^{n} &= \hat{v}_{IMU}^{n} + \omega_{in}^{n}\times C_{b}^{n}l^b - C_{b}^{n}\omega_{ib}^{b}\times l^b \end{aligned} r^GPS,inv^GPS,in=r^IMUn+DR−1Cbnlb=v^IMUn+ωinn×Cbnlb−Cbnωibb×lb
其中
v ^ G P S , i n = v ^ I M U n − C b n ω n b b × l b = v ^ I M U n − C b n ( ω n i b + ω i b b ) × l b = v ^ I M U n + C b n ω i n b × l b − C b n ω i b b × l b = v ^ I M U n + C b n ω i n b × C n b C b n l b − C b n ω i b b × l b = v ^ I M U n + ω i n n × C b n l b − C b n ω i b b × l b \begin{aligned} \hat{v}_{GPS,i}^{n} &= \hat{v}_{IMU}^{n} - C_{b}^{n}\omega_{nb}^{b}\times l^b\\ &= \hat{v}_{IMU}^{n} - C_{b}^{n}(\omega_{ni}^{b} + \omega_{ib}^{b})\times l^b\\ &= \hat{v}_{IMU}^{n} + C_{b}^{n}\omega_{in}^{b}\times l^b - C_{b}^{n}\omega_{ib}^{b}\times l^b\\ &= \hat{v}_{IMU}^{n} + C_{b}^{n}\omega_{in}^{b}\times C_{n}^{b}C_{b}^{n}l^b - C_{b}^{n}\omega_{ib}^{b}\times l^b\\ &= \hat{v}_{IMU}^{n} + \omega_{in}^{n}\times C_{b}^{n}l^b - C_{b}^{n}\omega_{ib}^{b}\times l^b\\ \end{aligned} v^GPS,in=v^IMUn−Cbnωnbb×lb=v^IMUn−Cbn(ωnib+ωibb)×lb=v^IMUn+Cbnωinb×lb−Cbnωibb×lb=v^IMUn+Cbnωinb×CnbCbnlb−Cbnωibb×lb=v^IMUn+ωinn×Cbnlb−Cbnωibb×lb根据上式可以导出观测方程,首先导出位置的观测方程:
r ^ G P S , i n = r ^ I M U n + D R − 1 C ^ b n l b r ^ G P S , i n = r I M U n + δ r I M U n + D R − 1 ( I − ϕ × ) l n r ^ G P S , i n − r I M U n + D R − 1 l n = δ r I M U n + D R − 1 l n × ϕ \begin{aligned} \hat{r}_{GPS,i}^{n} &= \hat{r}_{IMU}^{n} + D_{R}^{-1}\hat{C}_{b}^{n} l^b\\ \hat{r}_{GPS,i}^{n} &= r_{IMU}^{n} + \delta r_{IMU}^{n} + D_{R}^{-1}(I-\phi\times)l^n\\ \hat{r}_{GPS,i}^{n} - r_{IMU}^{n} + D_{R}^{-1}l^n &= \delta r_{IMU}^{n} + D_{R}^{-1}l^n\times\phi \\ \end{aligned} r^GPS,inr^GPS,inr^GPS,in−rIMUn+DR−1ln=r^IMUn+DR−1C^bnlb=rIMUn+δrIMUn+DR−1(I−ϕ×)ln=δrIMUn+DR−1ln×ϕ然后再导出速度的观测方程:
v ^ G P S , i n = v ^ I M U n + ω i n n × C ^ b n l b − C ^ b n ω i b b × l b v ^ G P S , i n = v I M U n + δ v I M U n + ω i n n × ( I + ϕ × ) C b n l b − ( I + ϕ × ) C b n ω i b b × l b v ^ G P S , i n = v I M U n + δ v I M U n + ω i n n × l n + ω i n n × ϕ × l n − C b n ω i b b × l b − ϕ × C b n ω i b b × l b v ^ G P S , i n = v I M U n + δ v I M U n + ω i n n × l n − ω i n n × l n × ϕ − C b n ω i b b × l b + C b n ω i b b × l b × ϕ v ^ G P S , i n − v I M U n − ω i n n × l n + C n b ω i b b × l b = δ v I M U n − ω i n n × l n × ϕ + C b n ω i b b × l b × ϕ \begin{aligned} \hat{v}_{GPS,i}^{n} &= \hat{v}_{IMU}^{n} + \omega_{in}^{n}\times \hat{C}_{b}^{n}l^b - \hat{C}_{b}^{n}\omega_{ib}^{b}\times l^b \\ \hat{v}_{GPS,i}^{n} &= v_{IMU}^{n} +\delta v_{IMU}^{n} + \omega_{in}^{n}\times (I+\phi\times) C_{b}^{n}l^b - (I+\phi\times)C_{b}^{n}\omega_{ib}^{b}\times l^b \\ \hat{v}_{GPS,i}^{n} &= v_{IMU}^{n} +\delta v_{IMU}^{n} + \omega_{in}^{n}\times l^n +\omega_{in}^{n}\times \phi\times l^n - C_{b}^{n}\omega_{ib}^{b}\times l^b -\phi\times C_{b}^{n}\omega_{ib}^{b}\times l^b \\ \hat{v}_{GPS,i}^{n} &= v_{IMU}^{n} +\delta v_{IMU}^{n} + \omega_{in}^{n}\times l^n - \omega_{in}^{n}\times l^n\times\phi - C_{b}^{n}\omega_{ib}^{b}\times l^b + C_{b}^{n}\omega_{ib}^{b}\times l^b\times\phi \\ \hat{v}_{GPS,i}^{n} &- v_{IMU}^{n} - \omega_{in}^{n}\times l^n + C_{n}^{b}\omega_{ib}^{b}\times l^b = \delta v_{IMU}^{n} - \omega_{in}^{n}\times l^n\times\phi + C_{b}^{n}\omega_{ib}^{b}\times l^b\times\phi \\ \end{aligned} v^GPS,inv^GPS,inv^GPS,inv^GPS,inv^GPS,in=v^IMUn+ωinn×C^bnlb−C^bnωibb×lb=vIMUn+δvIMUn+ωinn×(I+ϕ×)Cbnlb−(I+ϕ×)Cbnωibb×lb=vIMUn+δvIMUn+ωinn×ln+ωinn×ϕ×ln−Cbnωibb×lb−ϕ×Cbnωibb×lb=vIMUn+δvIMUn+ωinn×ln−ωinn×ln×ϕ−Cbnωibb×lb+Cbnωibb×lb×ϕ−vIMUn−ωinn×ln+Cnbωibb×lb=δvIMUn−ωinn×ln×ϕ+Cbnωibb×lb×ϕ
5.2 轮速计
5.3 Lidar
相关文章:

INS 量测更新
5 量测更新 5.1 GNSS位置及速度更新 r ^ G P S , i n r ^ I M U n D R − 1 C b n l b v ^ G P S , i n v ^ I M U n ω i n n C b n l b − C b n ω i b b l b \begin{aligned} \hat{r}_{GPS,i}^{n} & \hat{r}_{IMU}^{n} D_{R}^{-1}C_{b}^{n} l^b\\ \hat{v}_{GPS…...

【ssh基础知识】
ssh基础知识 常用命令登录流程配置文件ssh密钥登录生成密钥上传公钥关闭密码登录 ssh服务管理查看日志ssh端口转发 ssh(ssh客户端)是一个用于登录到远程机器并在远程机器上执行命令的程序。 它旨在提供安全的加密通信在不安全的网络上的两个不受信任的主…...

04 开发第一个组件
概述 在Vue3中,一个组件就是一个.vue文件。 在本小节中,我们来开发第一个Vue3组件。这个组件的功能非常的简单,只需要在浏览器上输出一个固定的字符串”欢迎跟着Python私教一起学Vue3“即可。 实现步骤 第一步:新增src/compon…...

【Unity】如何让Unity程序一打开就运行命令行命令
【背景】 Unity程序有时依赖于某些服务去实现一些功能,此时可能需要类似打开程序就自动运行Windows命令行命令的功能。 【方法】 using UnityEngine; using System.Diagnostics; using System.Threading.Tasks; using System.IO; using System.Text...
Web前端-HTML(表格与表单)
文章目录 1.表格与表单1.1 概述 2.表格 table2.1 表格概述2.2. 创建表格2.3 表格属性2.4. 表头单元格标签th2.5 表格标题caption(了解)2.6 合并单元格(难点)2.7 总结表格 3. 表单标签(重点)3.1 概述3.2 form表单3.3 input 控件(重点)type 属性value属性值…...

Android RecycleView实现平滑滚动置顶和调整滚动速度
目录 一、滑动到指定位置(target position)并且置顶 1. RecycleView默认的几个实现方法及缺陷 2. 优化源码实现置顶方案 二、调整平移滑动速率 三、其他方案:置顶、置顶加偏移、居中 1. 其他置顶方案 2. 置顶加偏移 3. 滚动居中 在实…...

跳跃游戏 + 45. 跳跃游戏 II
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。 示例 1: 输…...
)
在Django中使用多语言(i18n)
在Django中使用多语言 配置中间件 MIDDLEWARE [......django.contrib.sessions.middleware.SessionMiddleware,django.middleware.locale.LocaleMiddleware, # 此行重点django.middleware.common.CommonMiddleware,...... ]配置翻译文件目录 根目录下创建目录locale # 国…...
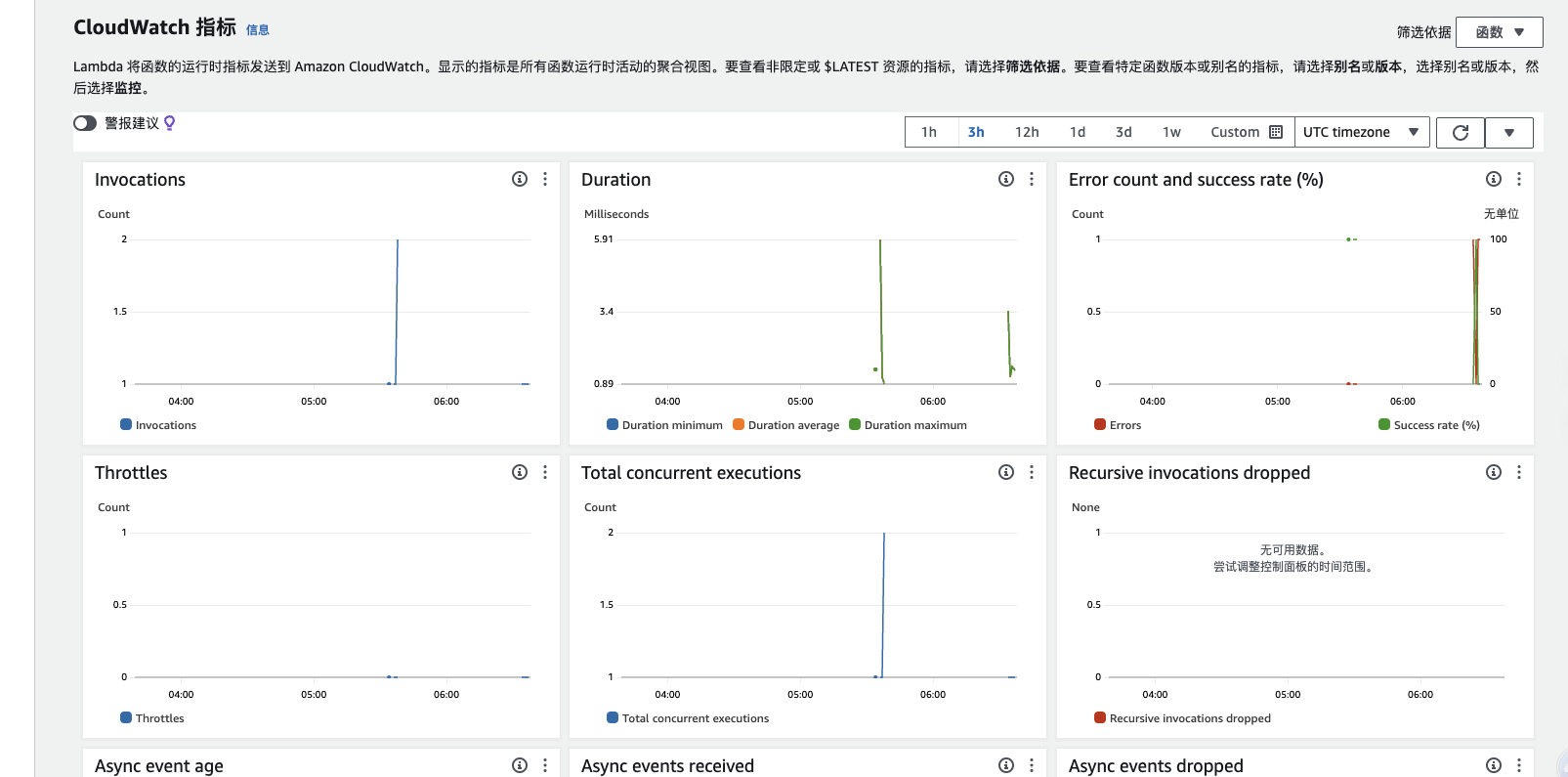
高性价比AWS Lambda无服务体验
前言 之前听到一个讲座说到AWS Lambda服务,基于Serverless无服务模型,另外官网还免费提供 100 万个请求 按月,包含在 AWS 免费套餐中是真的很香,对于一些小型的起步的网站或者用户量不大的网站,简直就是免费ÿ…...
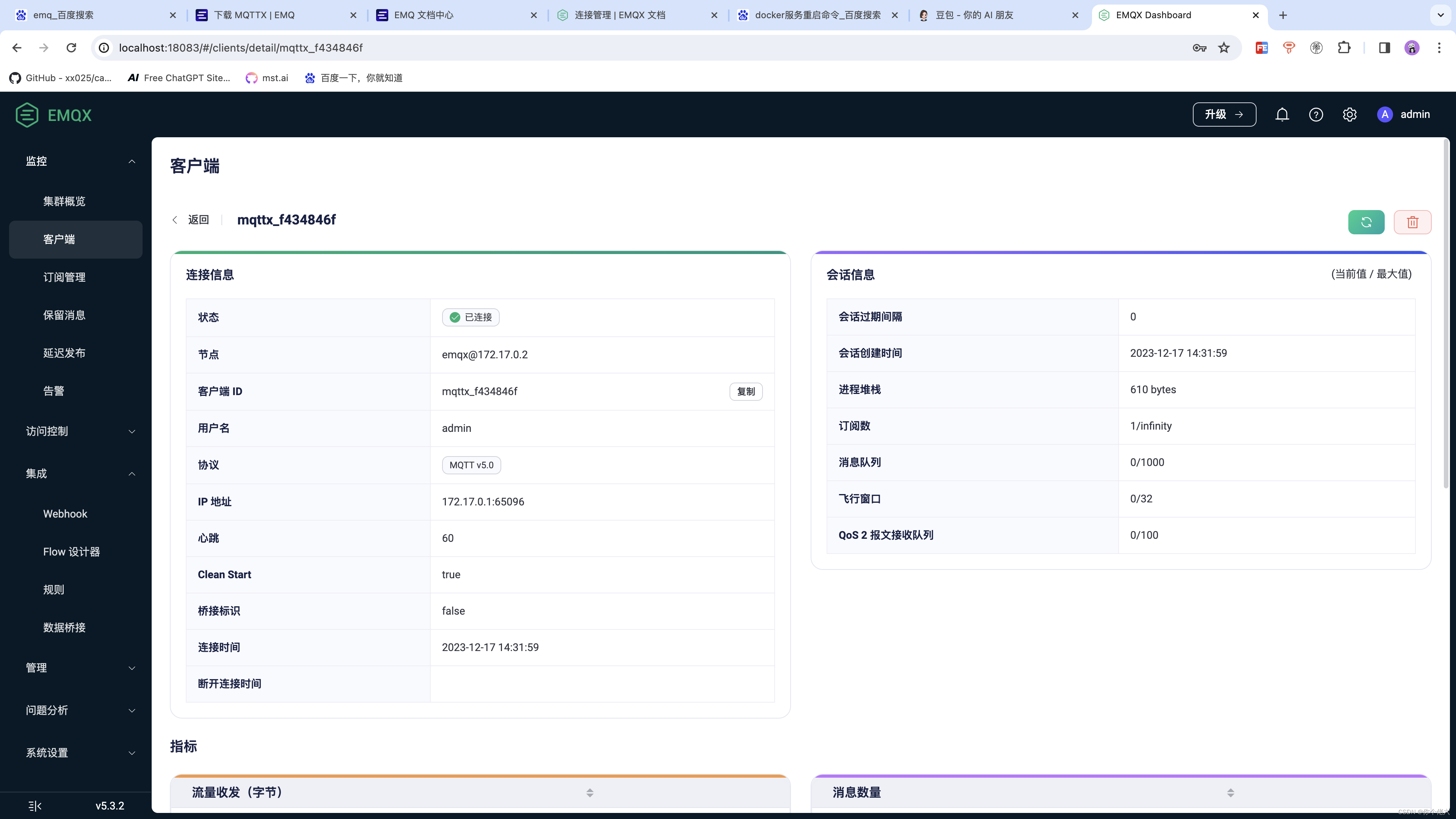
【物联网】EMQX(二)——docker快速搭建EMQX 和 MQTTX客户端使用
一、前言 在上一篇文章中,小编向大家介绍了物联网必然会用到的消息服务器EMQ,相信大家也对EMQ有了一定的了解,那么接下来,小编从这篇文章正式开始展开对EMQ的学习教程,本章节来记录一下如何对EMQ进行安装。 二、使用…...
2023 亚马逊云科技 re:lnvent 大会探秘: Amazon Connect 全渠道云联络中心
2023 亚马逊云科技 re:lnvent 大会探秘: Amazon Connect 全渠道云联络中心 前言一. Amazon Connect 介绍 🗺️二. Amazon Connect 使用教程 🗺️1.我们打开URl链接找到对应服务2.输入Amazon Connect选中第一个点击进入即可;3.在进入之后我们就…...

鸿蒙开发之用户隐私权限申请
一、简介 鸿蒙开发过程中可用于请求的权限一共有两种:normal和system_basic。以下内容摘自官网: normal权限 normal 权限允许应用访问超出默认规则外的普通系统资源。这些系统资源的开放(包括数据和功能)对用户隐私以及其他应用带…...

Docker笔记:简单部署 nodejs 项目和 golang 项目
docker 简单的维护 nodejs 项目容器 1 )Nodejs 程序 const express require(express) const app express()app.get(/, (req, res) > {res.send(首页) })app.get(/news, (req, res) > {res.send(news) })// dokcer 做端口映射不要指定ip app.listen(3000)2…...

java内置的数据结构
Java语言提供了许多内置的数据结构,包括: 1. 数组(Array):数组是最基本的数据结构之一,它是一个有序的元素集合,每个元素都有一个对应的索引。在Java中,数组可以通过声明和初始化来创…...
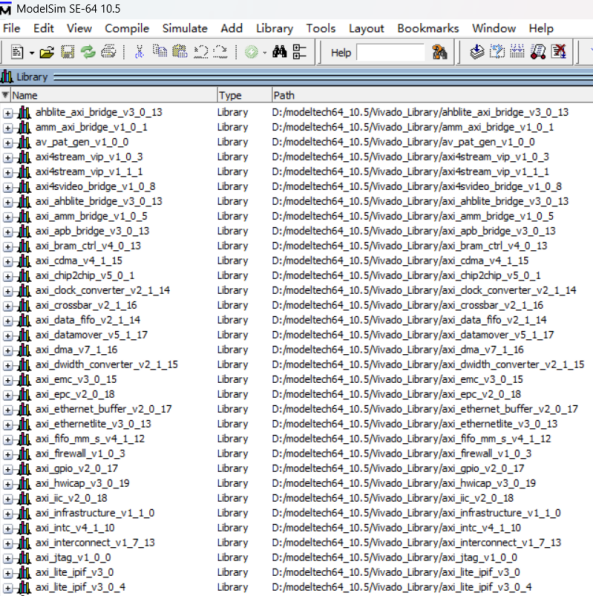
轻松搭建FPGA开发环境:第三课——Vivado 库编译与设置说明
工欲善其事必先利其器,很多人想从事FPGA的开发,但是不知道如何下手。既要装这个软件,又要装那个软件,还要编译仿真库,网上的教程一大堆,不知道到底应该听谁的。所以很多人还没开始就被繁琐的开发环境搭建吓…...
PostgreSQL-Dropdb命令删除数据库)
【PostgreSQL】从零开始:(十一)PostgreSQL-Dropdb命令删除数据库
dropdb命令删除数据库 命令 [postgrespostgre-sql bin]$ dropdb --help dropdb removes a PostgreSQL database.Usage:dropdb [OPTION]... DBNAMEOptions:-e, --echo show the commands being sent to the server-f, --force try to terminate …...

UDP网络编程其他相关事项
netstat指令 netstat -an 可以查看当前主机网络情况,包括端口监听情况和网络连接情况。 netstat -an | more 可以分页显示。 要求在dos控制台下执行。 说明:(1)Listening表示某个端口在监听;(2…...

Redhat LINUX 9.3 + PG 16.1 搭建主备流复制
一直想搭建一个PG流复制,最近正好有一个新环境,操作系统是最新的,rhel 9.3,数据库是最新的 pg 16.1,借鉴了网上的步骤,尤其是小工到专家的内容,在此谢过。 1.安装环境 1)IP: 主:192.168.133.151…...

kafka设置消费者组
安装部署后 consumer.properties group.idtest-group 单机测试,自己开俩窗口,一个测试消费者,一个测试生产者(创建消息那步) 创建主题 bin/kafka-topics.sh --create --bootstrap-server localhost:9092 --replica…...

Worker-Thread设计模式
Worker-Thread模式类似于工厂流水线,有时也称为流水线设计模式。线程池在某种意义上也算是Worker-Thread模式的一种实现,线程池初始化时创建线程类似于在流水线等待工作的工人,提交给线程池的Runnable接口类似于需要加工的产品,Ru…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...
