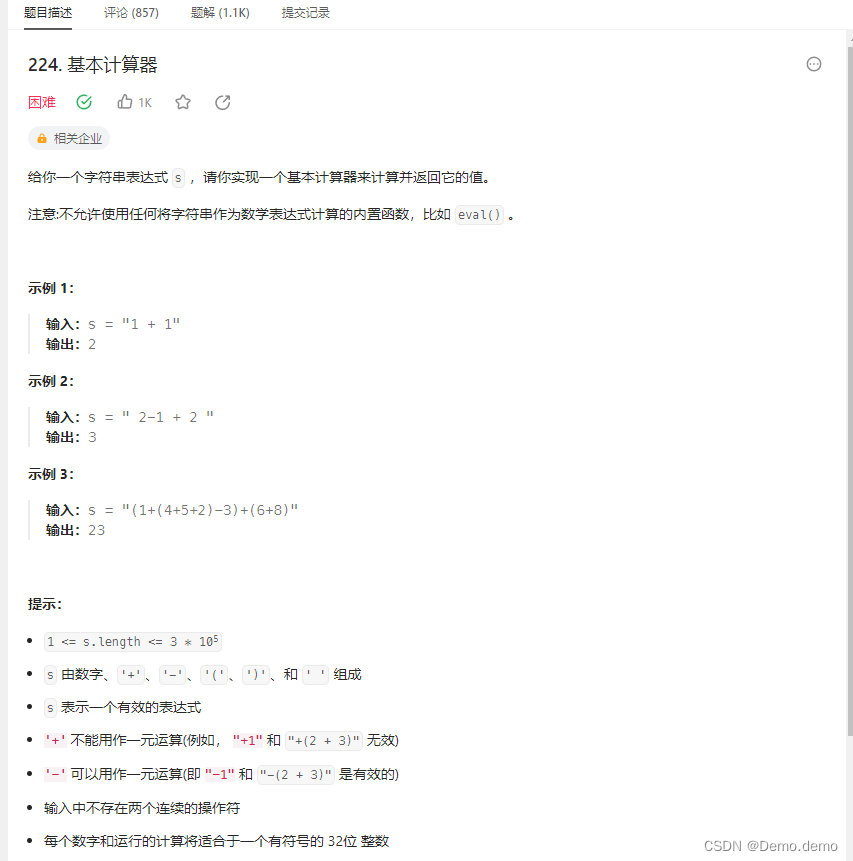
Leetcode刷题笔记题解(C++):224. 基本计算器
思路:
step 1:使用栈辅助处理优先级,默认符号为加号。
step 2:遍历字符串,遇到数字,则将连续的数字字符部分转化为int型数字。
step 3:遇到左括号,则将括号后的部分送入递归,处理子问题;遇到右括号代表已经到了这个子问题的结尾,结束继续遍历字符串,将子问题的加法部分相加为一个数字,返回。
step 4:当遇到符号的时候如果是+,得到的数字正常入栈,如果是-,则将其相反数入栈,如果是*,则将栈中内容弹出与后一个元素相乘再入栈。
step 5:最后将栈中剩余的所有元素,进行一次全部相加。
#include <stack>
#include <vector>
class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** 返回表达式的值* @param s string字符串 待计算的表达式* @return int整型*/int calculate(string s) {// write code herereturn function(s, 0)[0];}vector<int> function(string s,int index){stack<int>sk;long long num = 0;char op = '+';int i;for(i = index;i<s.size();i++){if(s[i]==' ') continue;//如果当前为数字else if(s[i]>='0'&&s[i]<='9'){num = num*10+s[i]-'0';//防止连续的数字if(i!=s.length()-1&&s[i+1]!=' ') continue;//如果为数字不执行下面的语句继续遍历,并且下一个字符不为空格}else if(s[i]=='('){//遇到左括号,从左括号开始第一个进行递归,并且下一个字符不为空格vector<int> res = function(s, i+1);num = res[0];//计算出括号中的计算值i = res[1];//得出遍历的下标位置if(i!=s.length()-1&&s[i+1]!=' ') continue;//如果还没结束字符串则继续遍历}switch (op) {case '+':sk.push(num);break;case '-':sk.push(0-num);break;case '*':int temp = sk.top();sk.pop();sk.push(temp*num);break;}num = 0;if(s[i] == ')') break;//遇到右括号则递归结束else op = s[i];}int sum = 0;//计算栈中的所有值的和while (!sk.empty()) {sum += sk.top();sk.pop();}return vector<int> {sum,i};}
};相关文章:

Leetcode刷题笔记题解(C++):224. 基本计算器
思路: step 1:使用栈辅助处理优先级,默认符号为加号。 step 2:遍历字符串,遇到数字,则将连续的数字字符部分转化为int型数字。 step 3:遇到左括号,则将括号后的部分送入递归&#x…...

还在为学MyBatis发愁?史上最全,一篇文章带你学习MyBatis
文章目录 前言一、📖MyBatis简介1.Mybatis历史2.MyBatis特性3.对比(其他持久化层技术) 二、📣搭建MyBatis1.开发环境2.创建maven工程3.创建MyBatis核心配置文件4.创建mapper接口5.创建MyBatis的映射文件6.通过junit测试功能7.加入…...
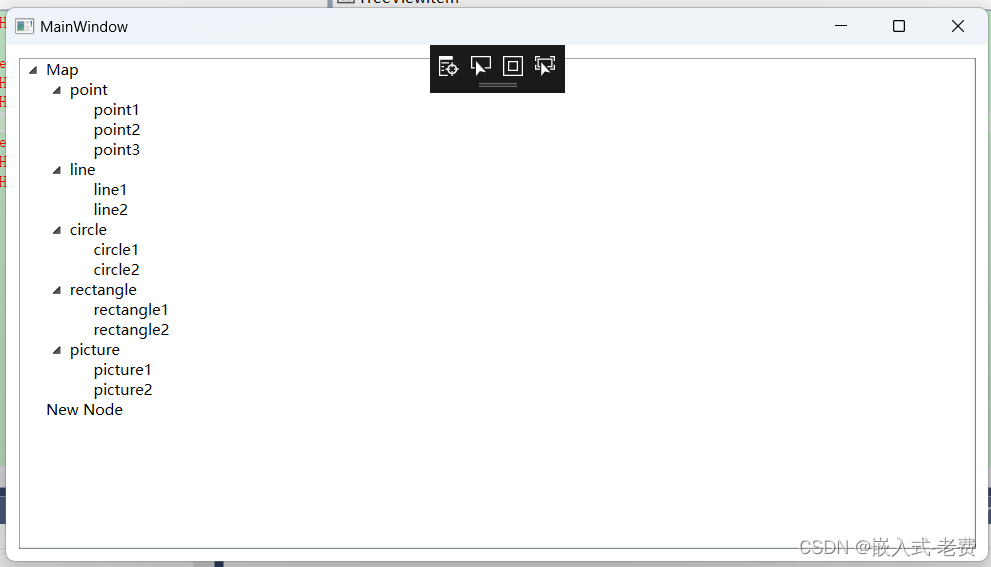
C# WPF上位机开发(树形控件在地图软件中的应用)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 前面我们聊过图形软件的开发方法。实际上,对于绘制的图形,我们一般还会用树形控件管理一下。举个例子,一个地图…...

【华为】文档中命令行约定格式规范(命令行格式规范、命令行行为规范、命令行参数格式、命令行规范)
文章目录 命令行约定格式**粗体:命令行关键字***斜体:命令行参数*[ ]:可选配置{ x | y | ... } 和 [ x | y | ... ]:选项{ x | y | ... }* 和 [ x | y | ... ]*:多选项&<1-n>:重复参数#ÿ…...
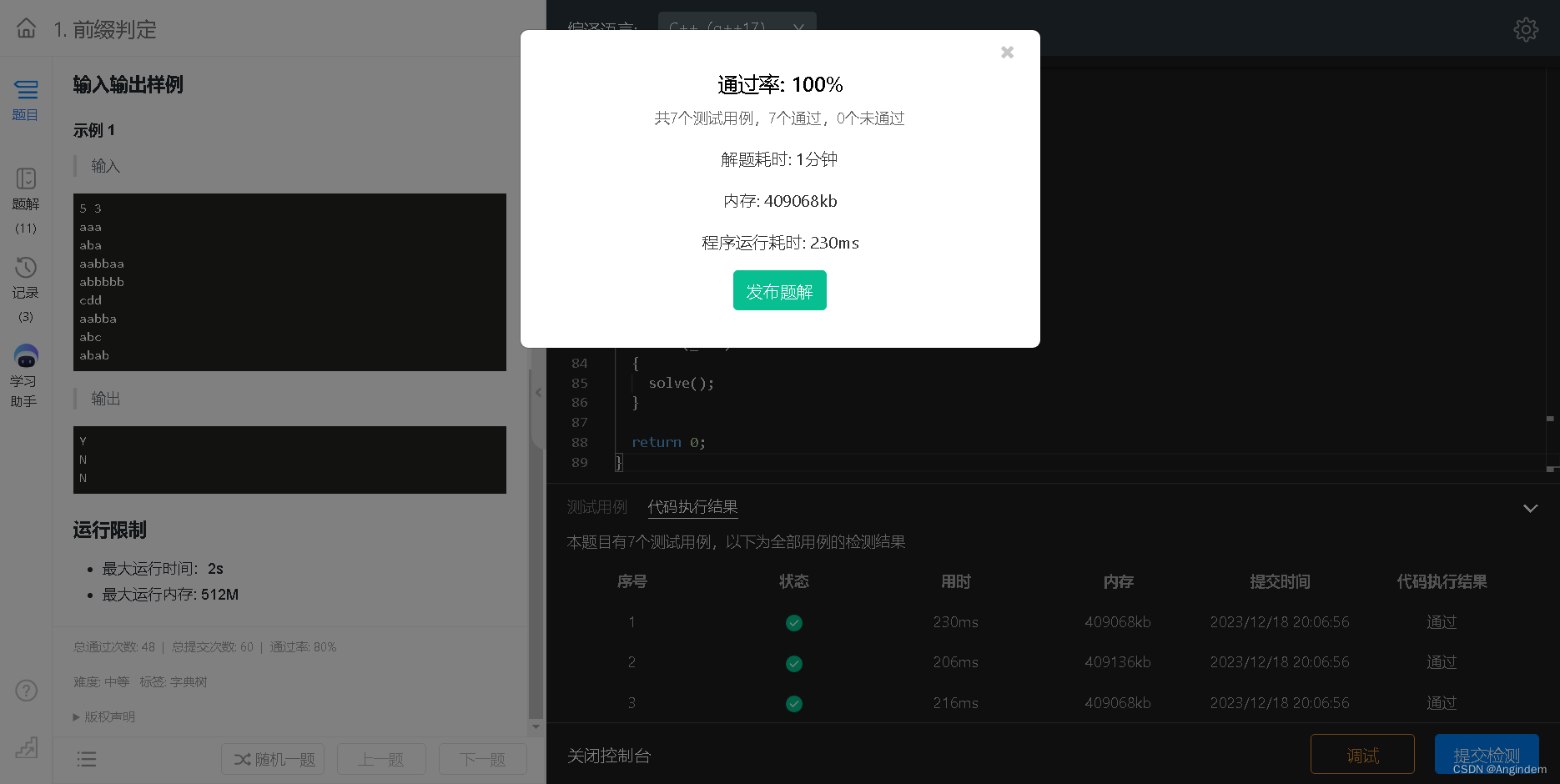
Trie 字典树(c++)(前缀)
题目链接:用户登录 题目: 样例: 输入 5 3 aaa aba aabbaa abbbbb cdd aabba abc abab 输出 Y N N 思路: 根据题目意思,要用到 Trie 字典树算法。 Trie 字典树,顾名思义,“字典”࿰…...
全球移动通信(2G/3G/4G/5G)频谱分布情况
一、概述 随着通信技术的不断发展,全球各国都在积极推进2G、3G、4G、5G网络的建设和应用。根据FCC统计,目前全球移动通信频谱分布如下: 二、分布 (一)俄罗斯 2G:主要使用900MHz和1800MHz两个频段。其中&…...
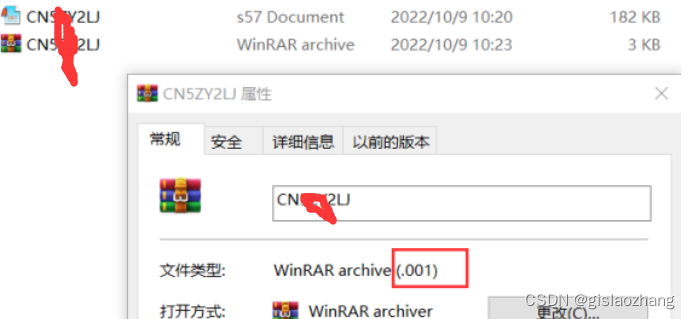
【04】GeoScene导出海图或者电子航道图000数据成果
1创建一个带有覆盖面和定义的产品 如果你没有已存在的S-57数据,你可以通过捕捉新的产品覆盖范围(多边形产品范围)及其所需的产品定义信息(产品元数据)来为新产品创建基础。 注: 如果你已经有一个S-57数据…...
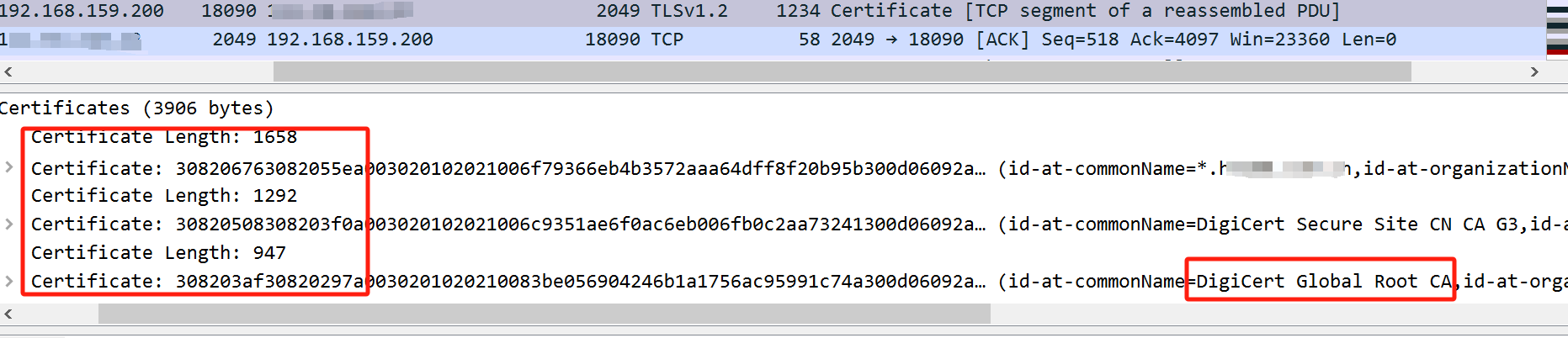
安卓端出现https请求失败(转)
背景# 某天早上,正在一个会议时,突然好几个同事被叫出去了;后面才知道,是有业务同事反馈到领导那里,我们app里面某个功能异常。 具体是这样,我们安卓版本的app是禁止截屏的(应该是app里做了拦…...
appium2.0.1安装完整教程+uiautomator2安装教程
第一步:根据官网命令安装appium(Install Appium - Appium Documentation) 注意npm前提是设置淘宝镜像: npm config set registry https://registry.npmmirror.com/ 会魔法的除外。。。 npm i --locationglobal appium或者 npm…...

Hbase的Rowkey设计
Hbase的Rowkey设计 rowkey设计 # 1)长度原则# 最大64KB,推荐长度10~100 byte# 最好设为8的倍数,能短则短,rowkey如果太长会影响性能。# 2)唯一原则:rowkey应该具备唯一性# 3)散列原则…...

软考机考考试第一批经验分享
由于机考的特殊性,考试环境与传统笔试环境有所不同。下面是与考试环境相关的总结: 草稿纸:考场提供足够数量的草稿纸,每位考生都会分发一张白纸作为草稿纸。在草稿纸上需要写上准考证号。如果不够用,可以向监考老师再次…...
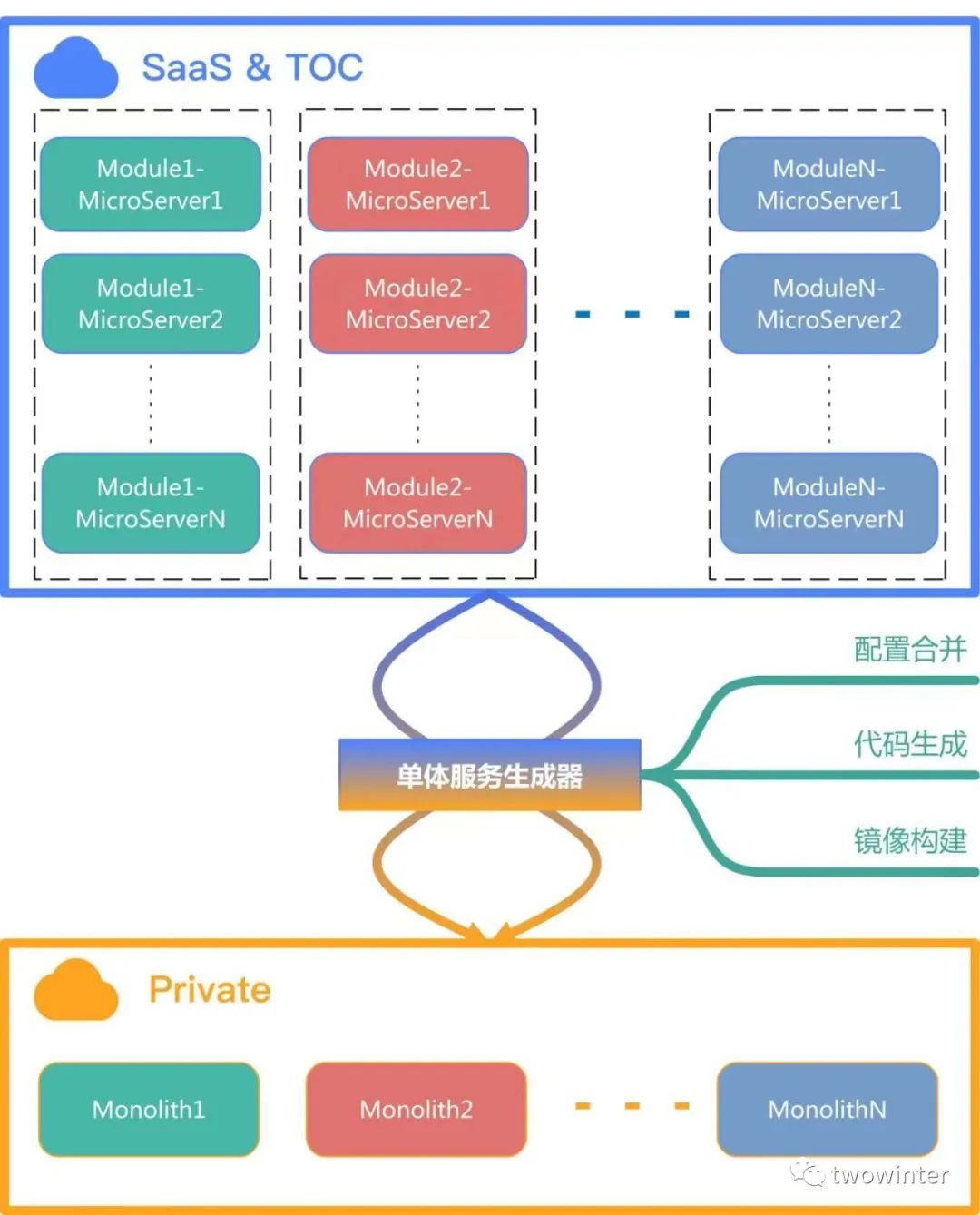
架构简洁之道有感,谈谈软件组件聚合的张力
配图由腾讯混元助手生成 这篇文章介绍了软件架构设计中组件设计思想,围绕“组件间聚合的张力”这个有意思的角度,介绍了概念,并且结合架构设计示例对这个概念进行了进一步阐述。 组件聚合?张力?这标题,有种…...
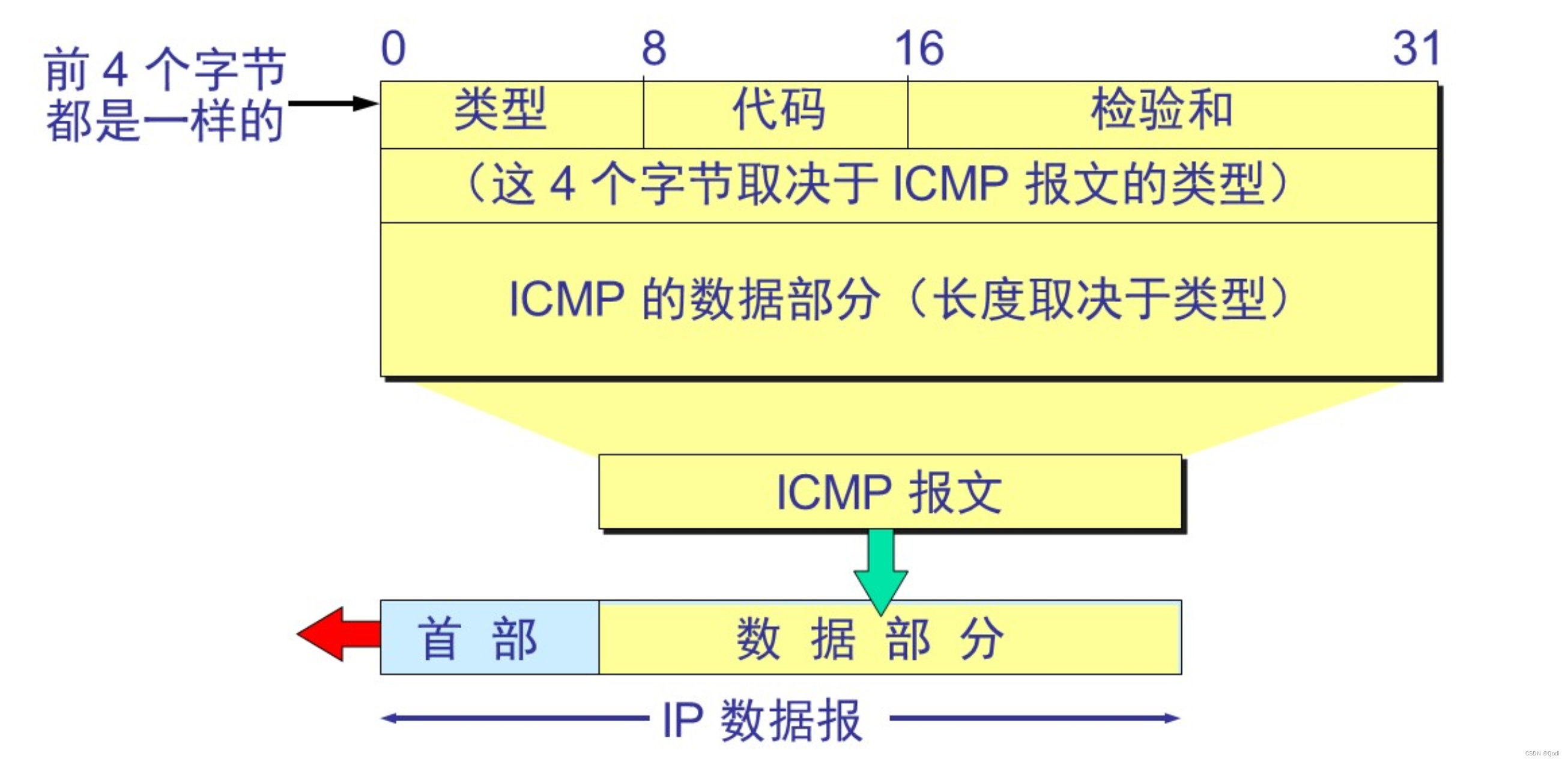
计算机网络 网络层上 | IP数据报,IP地址,ICMP,ARP等
文章目录 1 网络层的两个层面2 网络协议IP2.1 虚拟互联网络2.2 IP地址2.2.1 固定分类编址方式2.2.2 无分类编制CIDR2.2.3 MAC地址和IP地址区别 2.3 地址解析协议ARP2.3.1 解析过程 2.4 IP数据报格式 3 IP层转发分组流程4 国际控制报文协议ICMP4.1 ICMP格式结构4.2 分类4.2.1 差…...
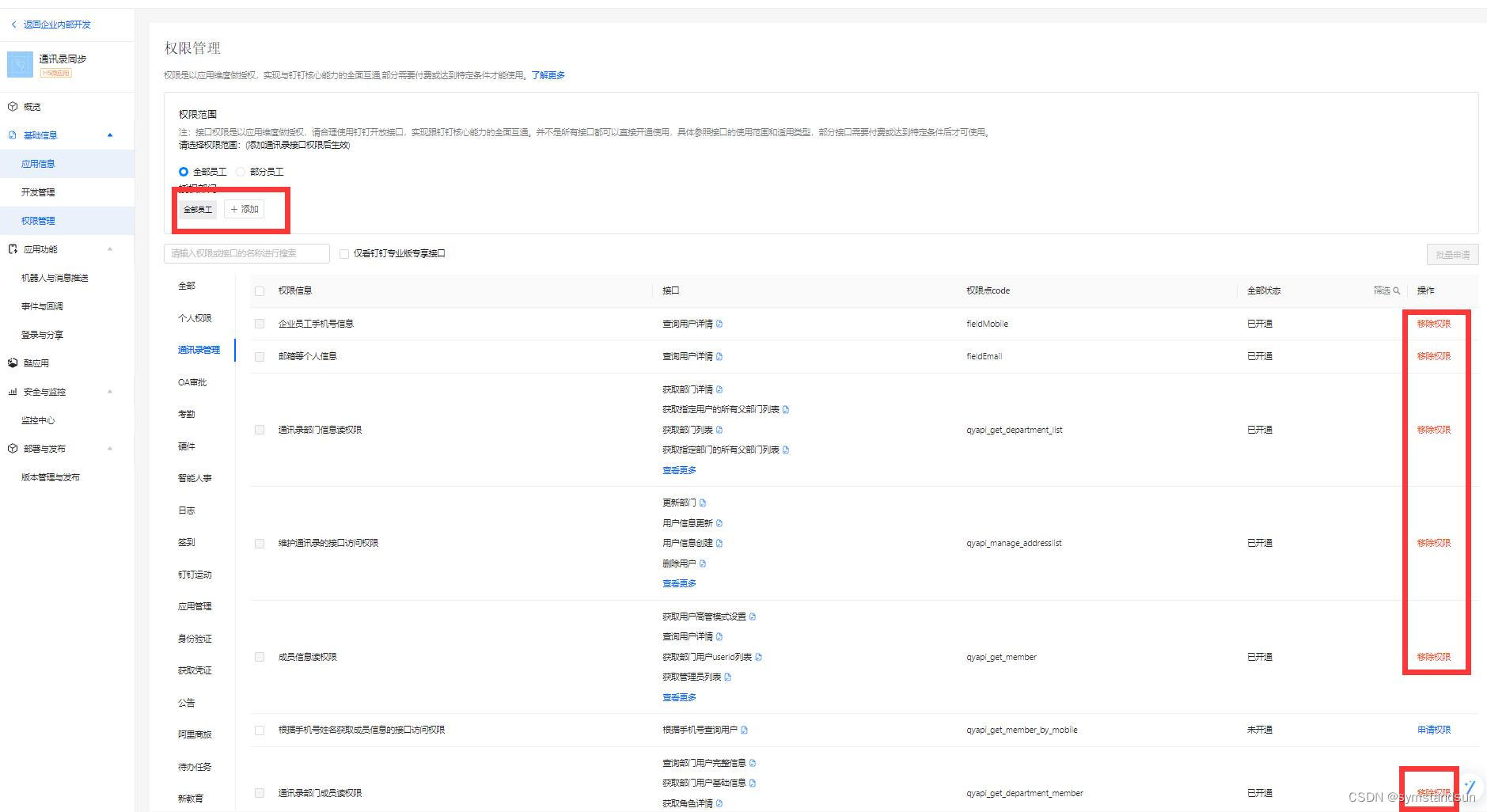
金智融门户(统一身份认证)同步数据至钉钉通讯录
前言:因全面使用金智融门户和数据资产平台,二十几个信息系统已实现统一身份认证和数据同步,目前单位使用的钉钉尚未同步组织机构和用户信息,职工入职、离职、调岗时都需要手工在钉钉后台操作,一是操作繁琐,二是钉钉通讯录更新不及时或经常遗漏,带来管理问题。通过金智融…...
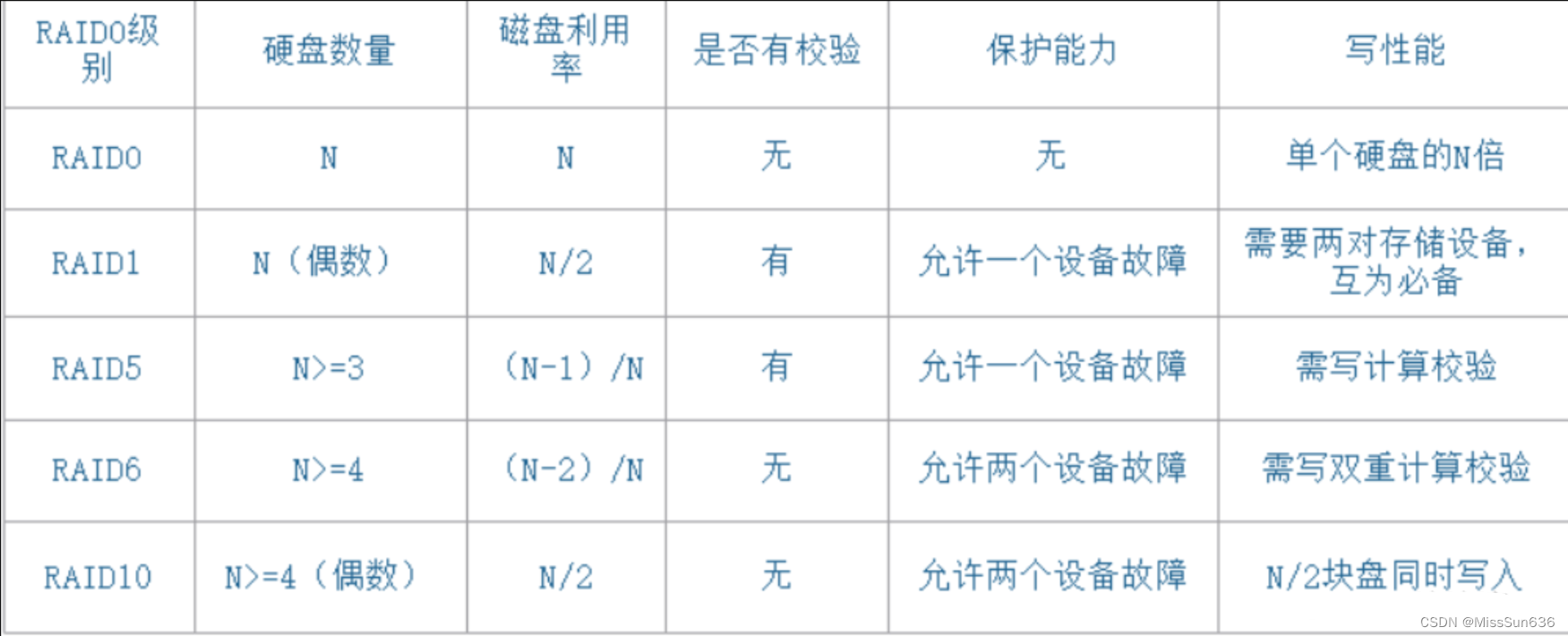
服务器RAID配置及功能介绍
服务器RAID配置及功能介绍 一、RAID磁盘阵列详解1.RAID磁盘阵列介绍2.RAID 03.RAID14.RAID35.RAID56.RAID67.RAID 10总结阵列卡介绍 一、RAID磁盘阵列详解 1.RAID磁盘阵列介绍 ①是Redundant Array of lndependent Disks的缩写中文简称为独立冗余磁盘阵列。 ②把多块独立的物…...

vue + element 实现鼠标左右滑动效果
我用了element中的走马灯+overflow-x: auto; html (复制后格式化一下) <div class"scroll" id"entrance"><el-carousel height"150px" :autoplay"false" :loop"false" arrow&q…...
gitlab 安装
1.安装依赖 sudo apt updatesudo apt-get upgradesudo apt-get install curl openssh-server ca-certificates postfix安装gitlab curl -s https://packages.gitlab.com/install/repositories/gitlab/gitlab-ce/script.deb.sh | sudo bash官网下载安装包 要选ubuntu focal 安…...
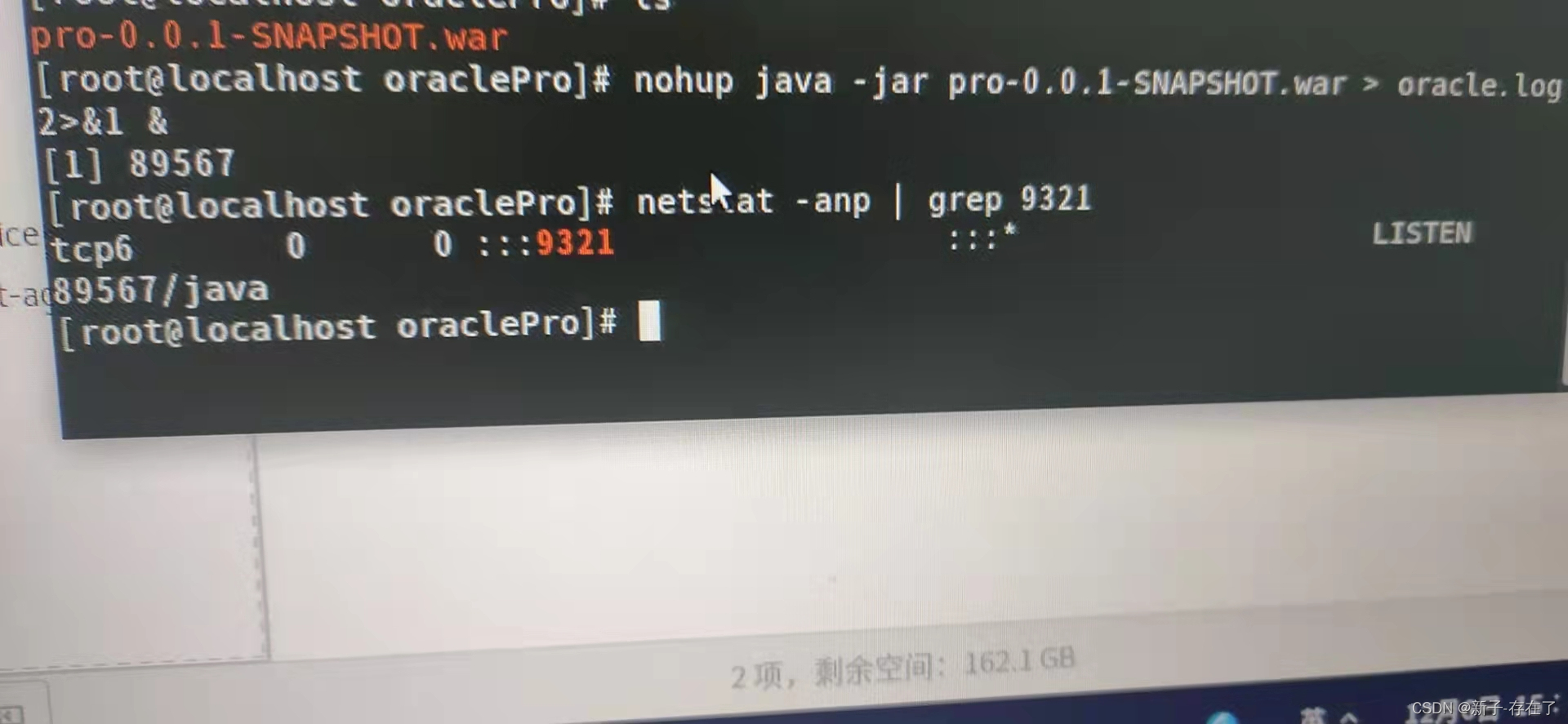
idea中定时+多数据源配置
因项目要求,需要定时从达梦数据库中取数据,并插入或更新到ORACLE数据库中 1.pom.xml <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-…...

Python---多任务的介绍
1. 提问 利用现学知识能够让两个函数或者方法同时执行吗? 不能,因为之前所写的程序都是单任务的,也就是说一个函数或者方法执行完成另外一个函数或者方法才能执行,要想实现这种操作就需要使用多任务。 多任务的最大好处是充分利用CPU资源&…...
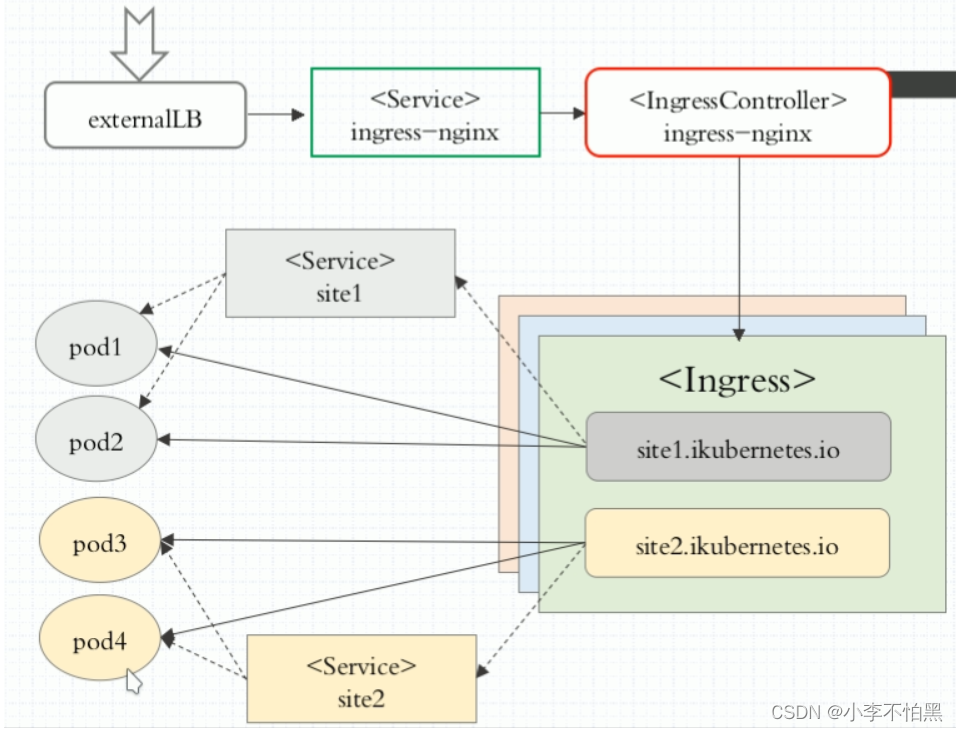
Kubernetes 的用法和解析 -- 4
一.Deployment 资源详解 如果Pod出现故障,对应的服务也会挂掉,所以Kubernetes提供了一个Deployment的概念 ,目的是让Kubernetes去管理一组Pod的副本,也就是副本集 ,这样就能够保证一定数量的副本一直可用,…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...
