Django去访问web api接口Object of type Session is not JSON serializable
解决方案:settings.py中加入 :SESSION_SERIALIZER = 'django.contrib.sessions.serializers.PickleSerializer'
事由:Django去访问一个web api接口,两次连接之间需要通过Session()保持身份验证。
def sendCode(request): mobile =json.loads(request.body).get("Mobile")http = requests.Session()result = http.get(f'http://127.0.0.1:8000/api/login?mobile={mobile}&func=send_code')request.session['http'] = httprequest.session['httpMobile'] = mobilereturn resultdef verifyCode(request): code =json.loads(request.body).get("code")mobile = request.session.get('httpMobile')http = request.session.get('http')result = http.get(f'http://127.0.0.1:8000/api/login?mobile={mobile}&func=verify_code&code={code}')return result提示:Object of type Session is not JSON serializable
加入SESSION_SERIALIZER = 'django.contrib.sessions.serializers.PickleSerializer' 后解决。
相关文章:

Django去访问web api接口Object of type Session is not JSON serializable
解决方案:settings.py中加入 :SESSION_SERIALIZER django.contrib.sessions.serializers.PickleSerializer 事由:Django去访问一个web api接口,两次连接之间需要通过Session()保持身份验证。 def sendCode(request): mobile jso…...
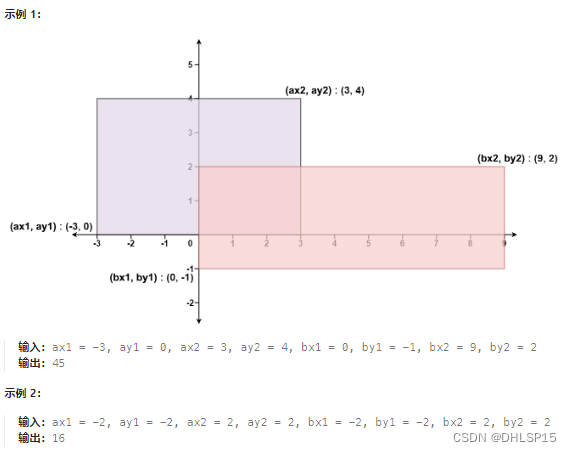
每日一题,二维平面
给你 二维 平面上两个 由直线构成且边与坐标轴平行/垂直 的矩形,请你计算并返回两个矩形覆盖的总面积。 每个矩形由其 左下 顶点和 右上 顶点坐标表示: 第一个矩形由其左下顶点 (ax1, ay1) 和右上顶点 (ax2, ay2) 定义。 第二个矩形由其左下顶点 (bx1, …...

【jupyter notebook】jupyter notebook 调用另一个jupyter notebook 的函数
总结 使用 %run 魔法命令将 Notebook 转换为py文件使用 nbimporter 库手动复制代码优点notebook最前面加上即可最基本方法就跟导入py文件一样,不会被执行一遍快缺点所有的代码都会执行一遍修改原文件就要重新转换,且 从自定义的 .py 文件中导入函数时&a…...

Linux--学习记录(3)
G重要编译参数 -g(GDB调试) -g选项告诉gcc产生能被GNU调试器GDB使用的调试信息,以调试程序编译带调试信息的可执行文件g -g hello.c -o hello编译过程: -E(预处理) g -E hello.c -o hello.i-S(编…...
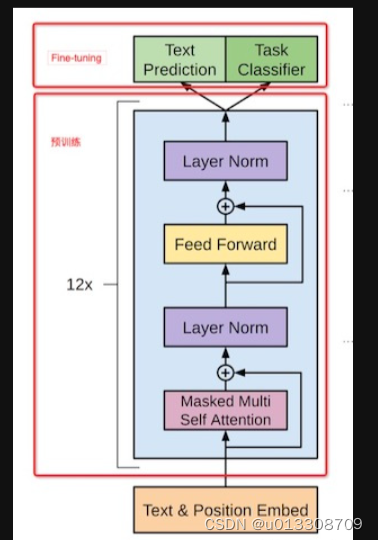
自然语言处理阅读第一弹
Transformer架构 encoder和decoder区别 Embeddings from Language Model (ELMO) 一种基于上下文的预训练模型,用于生成具有语境的词向量。原理讲解ELMO中的几个问题 Bidirectional Encoder Representations from Transformers (BERT) BERT就是原生transformer中的Encoder两…...

Spring Boot+Mybatis设置sql日志打印
在全局配置文件添加以下内容:logging.level.com.demo.mapperdebug,com.demo.mapper:src下的mapper路径,debug:设置日志打印级别为debug,亦可设置为:ERROR、WARN、INFO application.properties …...

步进电机电流设置的3种方法
本文介绍步进电机电流设置的3种方法。 步进电机电流设置包括运行电流(IRun)和保持电流(IHold)2种。电机运行时需要有较大电流以保证有足够的力矩使物体运动,而停止的时候,为了减少电机发热及降低功耗&…...

uniapp-使用返回的base64转换成图片
在实际开发的时候 需要后端实时的给我返回二维码 他给我返回的是加密后的base64字符串 我需要利用这个base64转换到canvas画布上展示 或者以图片的形式展示在页面内 在canvas画布上展示 使用官方的uni.getFileSystemManager().writeFile()方法可将base64码转成的二维码显示在…...

有机面条市场分析:到2026 年的复合年增长率为 5.4%
近年来,有机面条因其健康益处和可持续性而广受欢迎。由于消费者对健康和天然食品的需求不断增加,预计 全球有机面条市场将继续以显着速度增长。特别是中国市场,由于健康意识的提高以及对有机和天然产品的兴趣 增加,有机面条消费量…...

广州设计周落幕|值得被歌颂的奥力斯特岩板
12月11日,一年一度的广州设计周,为期四天的展会在广州保利世贸博览馆、广州国际采购中心和南丰国际会展中心三大展馆已落下帷幕。依旧熙攘,依旧热烈,远道而来的专家领导、媒体嘉宾、展商代表、外国友人、设计爱好者,风…...

WTN6系列语音芯片:PWM与DAC音频输出在PCB设计中的优势
随着科技的飞速发展,语音芯片在电子产品中的应用越来越广泛。其中,唯创知音的WTN6系列语音芯片凭借其卓越的性能和多样的功能,受到了市场的热烈欢迎。特别是其支持PWM和DAC两种音频输出方式的特点,使得工程师在PCB设计时能够更加灵…...
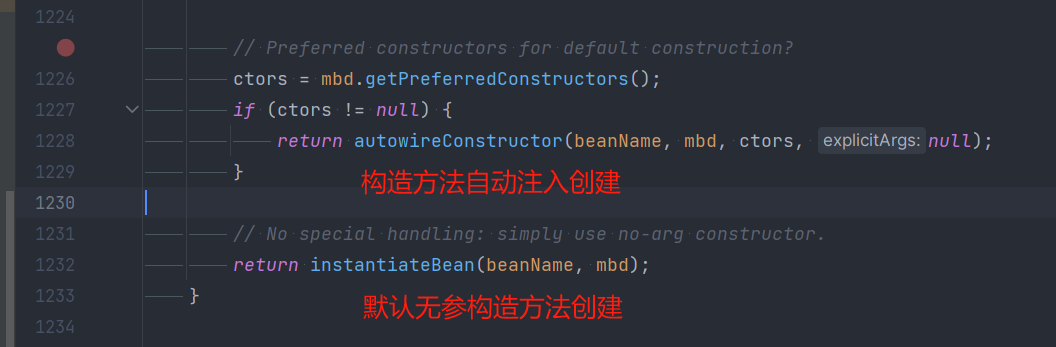
设计模式 原型模式 与 Spring 原型模式源码解析(包含Bean的创建过程)
原型模式 原型模式(Prototype模式)是指:用原型实例指定创建对象的种类,并且通过拷贝这些原型,创建新的对象。 原型模式是一种创建型设计模式,允许一个对象再创建另外一个可定制的对象,无需知道如何创建的细节。 工作原…...
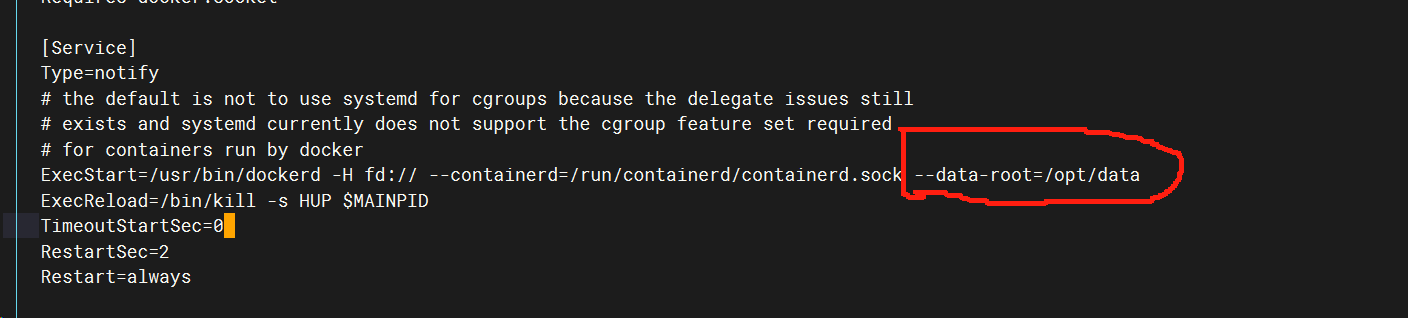
Docker介绍,Docker安装
docker镜像仓库官网 一、Docker的基本概念 1.Docker的三大核心组件 docker 镜像 --------docker images docker 仓库---------docker registeries docker 容器---------docker containers 2.Docker 镜像 Docker镜像是运行docker容器时的只读模板,每一个镜像由一…...
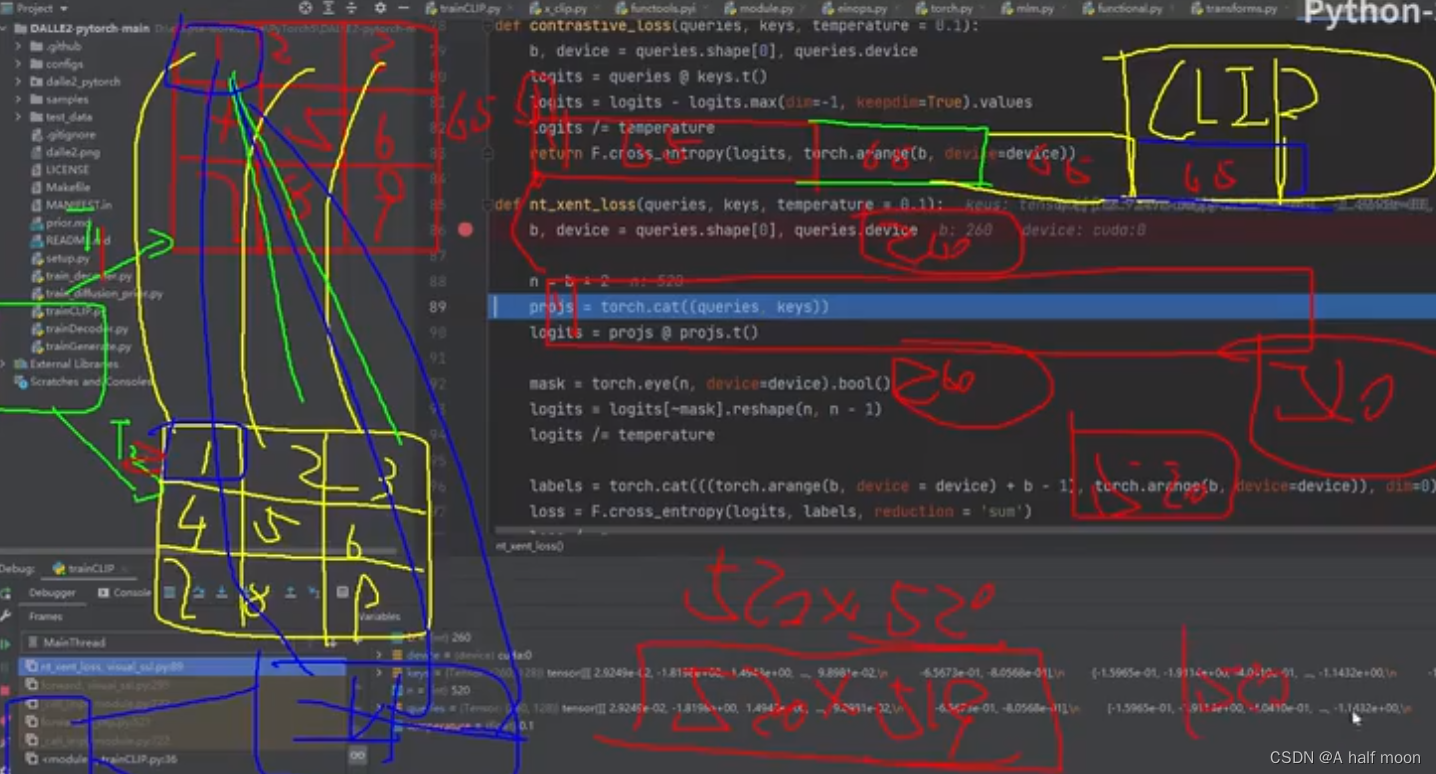
CLIP 对比学习 源码理解快速学习
最快的学习方法,理清思路,找视频讲解,看源码逻辑: CLIP 源码讲解 唐宇 输入: 图像-文本成对配对的数据 训练模型的过程(自己理解): 怎么做的?:利用数据内部…...
6.鸿蒙app_hap_DevEco如何真机调试模式_app安装在手机中
真机调试 手机》设置》关于手机》HarmonyOS版本》软件版本,连续单击10次启动开发者模式 然后:设置》系统和更新》开发人员选项》打开USB调试功能。 电脑USB连接手机,手机USB连接类型,传文件(不要选择仅充电…...
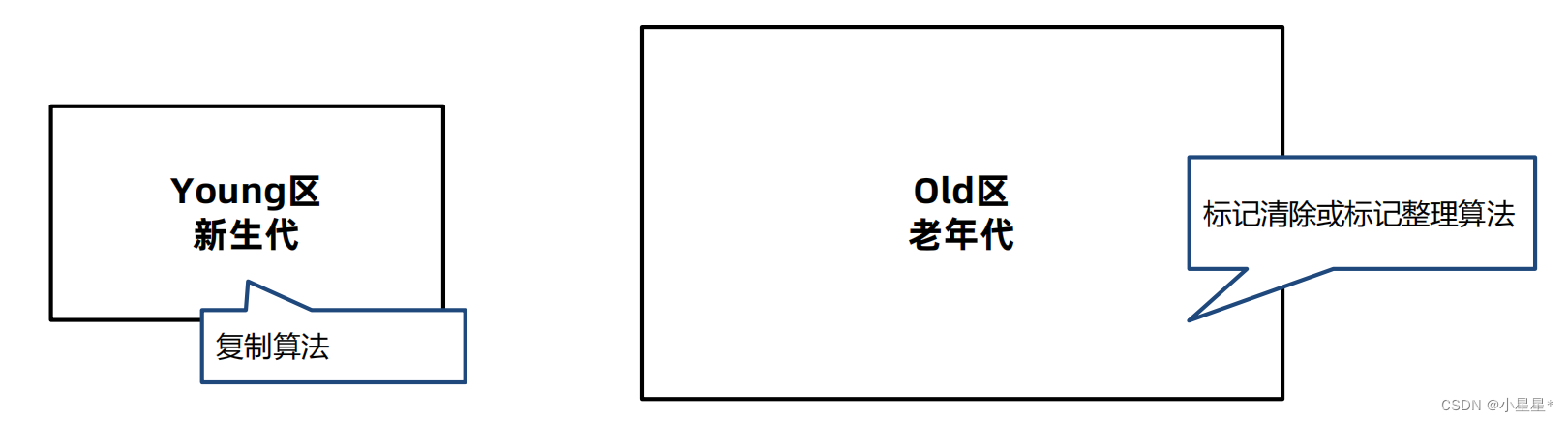
【JVM从入门到实战】(八)垃圾回收(1)
内存泄漏:指的是不再使用的对象在系统中未被回收,内存泄漏的积累可能会导致内存溢出 什么是垃圾回收 Java中为了简化对象的释放,引入了自动的垃圾回收(Garbage Collection简称GC)机制。通过垃 圾回收器来对不再使用的…...
-删除有序数组中的重复项)
LeeCode前端算法基础100题(12)-删除有序数组中的重复项
一、问题详情: 给你一个 非严格递增排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。 考虑 nums 的唯一元素的数量为 k ,你需要做以下事情确保你的题…...
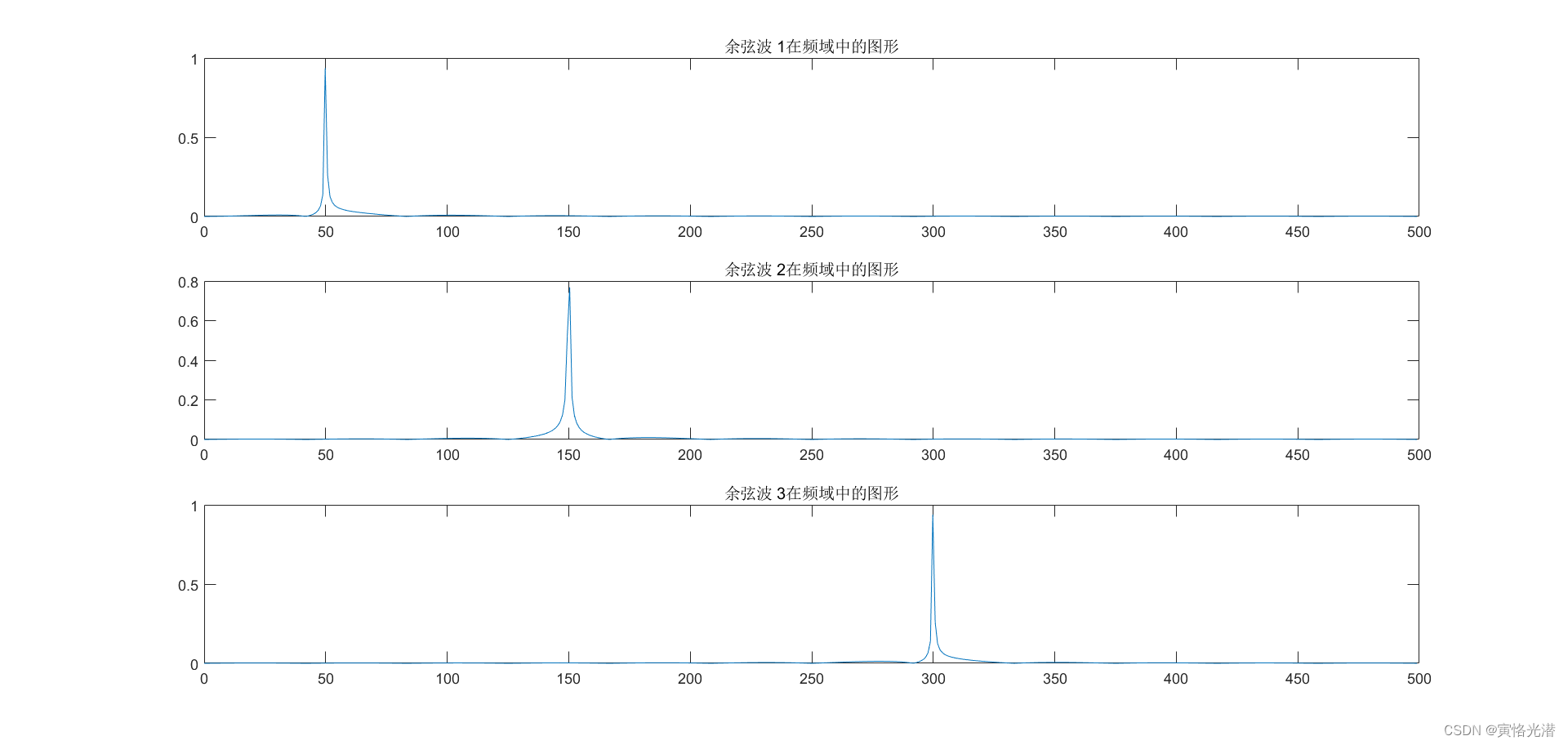
MATLAB图解傅里叶变换(初学者也可以理解)
1、概述 相信很多人对于傅里叶变换可能觉得比较复杂和有点难懂,其实不难,它只是一种积分变换。 傅里叶变换,表示能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。也就是说&qu…...

uni-app 用于开发H5项目展示饼图,使用ucharts 饼图示例
先下载ucharts H5示例源码: uCharts: 高性能跨平台图表库,支持H5、APP、小程序(微信小程序、支付宝小程序、钉钉小程序、百度小程序、头条小程序、QQ小程序、快手小程序、360小程序)、Vue、Taro等更多支持canvas的框架平台&#…...
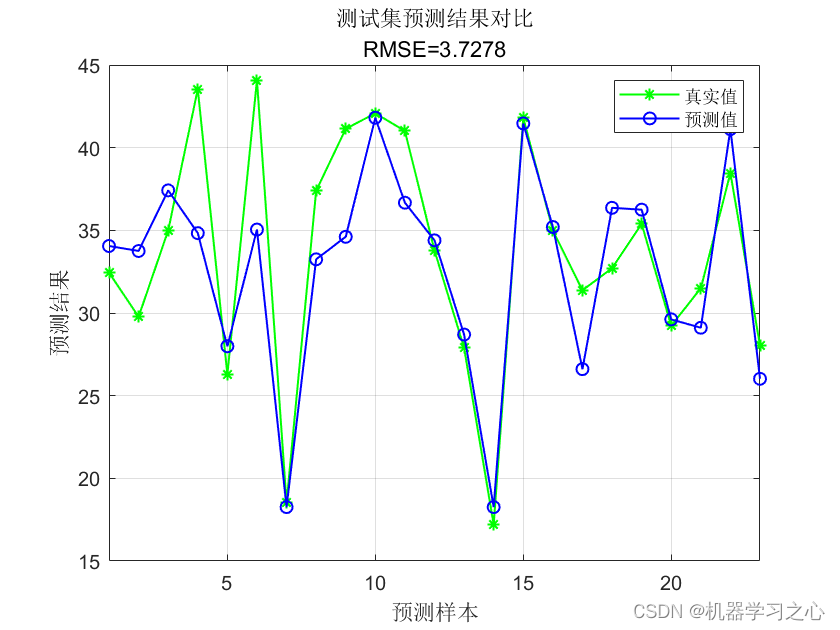
回归预测 | MATLAB实现SABO-LSTM基于减法平均优化器优化长短期记忆神经网络的多输入单输出数据回归预测模型 (多指标,多图)
回归预测 | MATLAB实现SABO-LSTM基于减法平均优化器优化长短期记忆神经网络的多输入单输出数据回归预测模型 (多指标,多图) 目录 回归预测 | MATLAB实现SABO-LSTM基于减法平均优化器优化长短期记忆神经网络的多输入单输出数据回归预测模型 &a…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...
