MATLAB图解傅里叶变换(初学者也可以理解)
1、概述
相信很多人对于傅里叶变换可能觉得比较复杂和有点难懂,其实不难,它只是一种积分变换。
傅里叶变换,表示能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。也就是说"任意"的函数通过一定的分解,都能够表示为正弦函数的线性组合的形式。而正弦函数在物理上是被充分研究而相对简单的函数类。因为特别好使,所以傅里叶变换在物理学、数论、组合数学、信号处理、概率、统计、密码学、声学、光学等领域都有着广泛的应用。
为什么使用正弦曲线来分解原函数呢?
因为正弦曲线的保真度。一个正弦曲线信号输入后,输出的仍是正弦曲线,只有幅度和相位可能发生变化,但是频率和波的形状仍是一样的。且只有正弦曲线才拥有这样的性质,所以我们会将原函数分解成正弦函数来处理。
2、连续傅里叶变换Continuous Fourier Transform,CFT
平时看到的傅里叶变换如果没有前缀,通常指的就是连续傅里叶变换。我们先来看一张图片:

从图片中我们可以了解到傅里叶的变换是时间域和频率域的互相转换,由于是连续的,所以使用的是积分。
平时我们所听到的音乐,就是随着时间的变化,听到不同的声音,乐器声和人声的各种混合,如果我想单独将人声给提取出来,这个时候我们可以使用傅里叶变换来处理,将这些不同的声音分解成各自的频率所表示的形式。这样我们就将本来很难处理的时域信号转换成了容易处理的频域信号了(信号的频谱),再利用一些工具对这些频域信号进行处理、加工即可。最后还可以利用傅里叶反变换将这些频域信号转换成时域信号。
3、离散傅里叶变换Discrete Fourier Transform,DFT
实际上我们的计算机是只能处理离散的数值信号,跟数学上的计算是有区别的,这些听到的连续的声音就需要做离散处理,因为计算机本质上只能处理0和1,所以这里不能使用积分,我们知道积分其实是极限的连续求和对吧,那我们这里就只能是离散求和了,而且不能处理无穷,计算机只能处理有限性,这个是前提条件。我们来看一张图片:
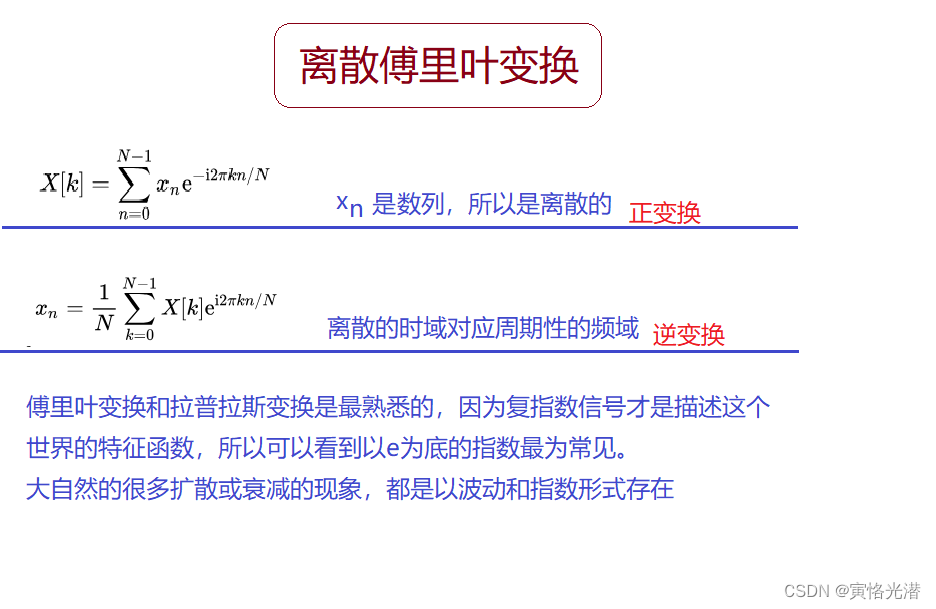
可以看到我们的离散傅里叶使用的是求和符号而不是上面的积分符号,在计算机里面我们就是使用这个DFT来处理信号。
直接使用DFT的定义计算的计算复杂度为 O(N²),而快速傅里叶变换(Fast Fourier Transform, FFT)可以将复杂度改进为 O(nlogn)。计算复杂度的降低以及数字电路计算能力的发展,使得DFT成为在信号处理领域十分实用且重要的方法。
从上面的分析来看,我们知道时域分析与频域分析是对信号的两个观察面。时域分析是以时间轴为坐标表示动态信号的关系;频域分析是把信号变为以频率轴为坐标表示出来。
一般来说,时域的表示较为形象与直观,频域分析则更为简练,剖析问题更为深刻和方便。信号分析的趋势是从时域向频域发展。然而,它们是互相联系,缺一不可,相辅相成的,它们的转换就是我们讲的傅里叶变换。
4、MATLAB应用
我们来看下具体的应用,在MATLAB中使用快速傅里叶变换FFT,将会是怎么样的。
先来看下fft函数的定义:
Y = fft(X) 用快速傅里叶变换 (fft) 算法计算 X 的离散傅里叶变换 (DFT)。
如果 X 是向量,则 fft(X) 返回该向量的傅里叶变换。
如果 X 是矩阵,则 fft(X) 将 X 的各列视为向量,并返回每列的傅里叶变换。
如果 X 是一个多维数组,则 fft(X) 将沿大小不等于 1 的第一个数组维度的值视为向量,并返回每个向量的傅里叶变换。Y = fft(X,n) 返回 n 点 DFT。如果未指定任何值,则 Y 的大小与 X 相同。
如果 X 是向量且 X 的长度小于 n,则为 X 补上尾零以达到长度 n。
如果 X 是向量且 X 的长度大于 n,则对 X 进行截断以达到长度 n。
如果 X 是矩阵,则每列的处理与在向量情况下相同。
如果 X 为多维数组,则大小不等于 1 的第一个数组维度的处理与在向量情况下相同Y = fft(X,n,dim) 返回沿维度 dim 的傅里叶变换。X 是矩阵,比如:
fft(X,n,1) 沿 X 的各列进行运算,返回每列的傅里叶变换;
fft(X,n,2) 沿 X 的各行进行运算,返回每行的傅里叶变换。
4.1、噪声信号Noise signal
我们来看具体的示例,使用傅里叶变换求噪声中隐藏的信号的频率分量(频谱分析)。
Fs = 1000; %采样频率
T = 1/Fs; %采样周期
L = 1500; %信号长度(1.5秒)
t = (0:L-1)*T; %时间%创建一个信号,其中包含幅值为0.7,频率为50Hz和幅值为1,频率为120Hz的正弦波
S = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t);
%添加一个标准差为2的噪声
X = S + 2*randn(size(t));
%绘制噪声时域信号。
plot(1000*t(1:50),X(1:50))
title('加了噪声的信号')
xlabel('t (毫秒)')
ylabel('X(t)')
通过查看这个时域信号X(t),我们很难确定频率分量,所以我们通过计算傅里叶变换来看频谱分析,这里使用的是快速傅里叶变换: Y = fft(X);
%计算双侧频谱P2,然后基于P2和偶数信号长度L计算单侧频谱P1,单侧频谱表示信号频率的幅度分布只从0到正频率一侧,正负频率是对称的
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);其中这里的abs是返回绝对值,但是这里是复数的形式,所以返回的是它们的模长(幅值),表示的是复数的大小,对于复数还有一个属性比较重要就是相位,表示的是复数的方向。
我们画图看下频谱对应的幅值:
f = Fs*(0:(L/2))/L;
plot(f,P1)
title('单侧幅值频谱')
xlabel('f (Hz)')
ylabel('|P1(f)|')可以看到在50Hz和120Hz的地方,幅值基本上还是接近0.7和1的,因为加了噪声的缘故,如果没有噪声那肯定是对应着0.7和1,这个大家可以试下。这里我们就可以看出,在时域坐标中,查看信号的频率分量比较困难,当我们使用傅里叶变换之后,在频域中查看信号就变得简单了。
4.2、高斯脉冲Gaussian Pulses
所谓的脉冲就是发送信号,接通一下,断开一下,这个就是一个脉冲,现在的步进电机和伺服电机的驱动都是通过脉冲来驱动。
高斯脉冲是具有高斯形状的时间强度曲线的脉冲,其中高斯函数如下:
其中a、b、c是常数,a决定了曲线的高度(峰值),b决定了曲线的中心位置(横坐标),c决定了曲线的宽度(标准差)。
因为高斯脉冲的时间强度曲线呈现出高斯分布的特点,所以它在时间和频率上都能达到较好的性能,从而在许多领域得到广泛的应用。
一起来看下高斯脉冲在时域转到频域的情况:
Fs = 100; %采样频率
t = -0.5:1/Fs:0.5; %时间
L = length(t); %信号长度
%高斯脉冲对应上面公式中的a、b、c了解
X = 1/(4*sqrt(2*pi*0.01))*(exp(-t.^2/(2*0.01)));%画图
plot(t,X)
title('时域中的高斯脉冲')
xlabel('Time (t)')
ylabel('X(t)')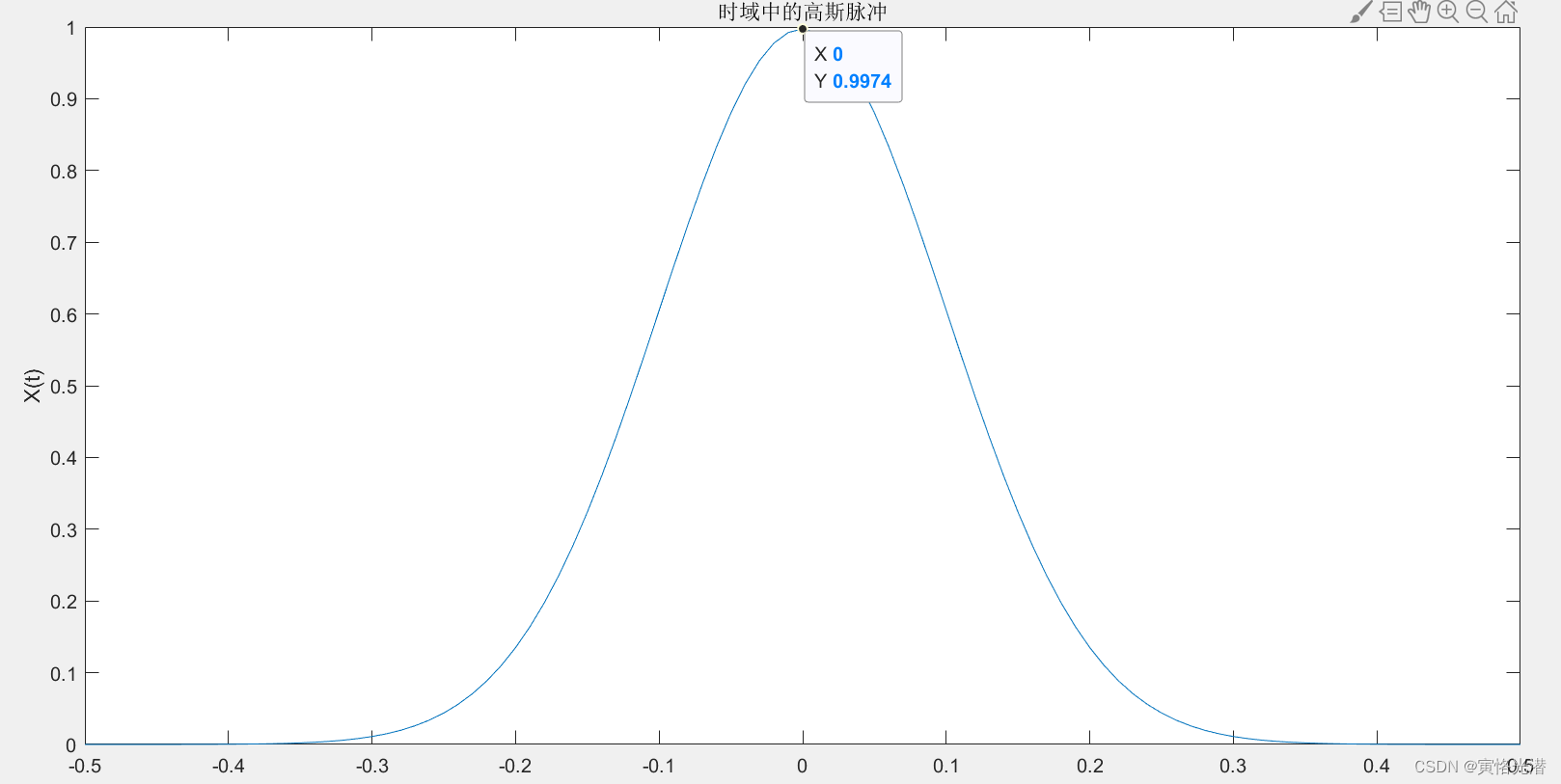
从图形中,我们可以看到是一个高斯分布,其中心点是0,峰值约为0.9974,另外公式看出宽度是0.1,这个函数在傅里叶变换中属于典型的特征函数。
在转换频域之前,首先从原始信号长度确定是下一个2次幂的新输入长度。当信号长度不等于2的幂时,使用 nextpow2 函数可提升 fft 的性能,使用的是尾随零填充信号。
n = 2^nextpow2(L);
%将高斯脉冲转换为频域。
Y = fft(X,n);%length(X):101,n:128,所以length(Y)是128
%画图
f = Fs*(0:(n/2))/n;
P = abs(Y/n);plot(f,P(1:n/2+1))
title('频域中的高斯脉冲')
xlabel('Frequency (f)')
ylabel('|P(f)|')
代码中的nextpow2函数,返回的是下一个2次幂大于等于这些值(绝对值)的指数,比如:
a = [1 -2 3 -4 5 9 519];
p = nextpow2(a)
p =0 1 2 2 3 4 102.^p 或者 pow2(p)
ans =1 2 4 4 8 16 1024
4.3、余弦波
我们来看下最常见的一个波形,比较它们不同频率的情况:
Fs = 1000; %采样频率
T = 1/Fs; %采样周期
L = 1000; % 信号长度
t = (0:L-1)*T; % 时间%三个余弦波,区别就是频率不一样
x1 = cos(2*pi*50*t); %50Hz
x2 = cos(2*pi*150*t); %150Hz
x3 = cos(2*pi*300*t); %300Hz
% 组合成一个矩阵
X = [x1; x2; x3];%画出每个余弦波前100个条目
for i = 1:3subplot(3,1,i)plot(t(1:100),X(i,1:100))title(['余弦波 ',num2str(i),' 的时域图形'])
end
这里我们发现三个余弦波,只能说往下的余弦波的频率比上面的要大,还是不能很清晰的表现出其本质,我们将其转换到频域空间看下是什么效果:
%同样的性能考虑,使用nextpow2函数定义新长度
n = 2^nextpow2(L);
%接下来就计算傅里叶变换
dim = 2;
Y = fft(X,n,dim);%计算每个信号的双侧频谱和单侧频谱
P2 = abs(Y/L);
P1 = P2(:,1:n/2+1);
P1(:,2:end-1) = 2*P1(:,2:end-1);%在频域图形里面,画出每一个余弦波的单侧幅值频谱
for i=1:3subplot(3,1,i)plot(0:(Fs/n):(Fs/2-Fs/n),P1(i,1:n/2))title(['余弦波 ',num2str(i),'在频域中的图形'])
end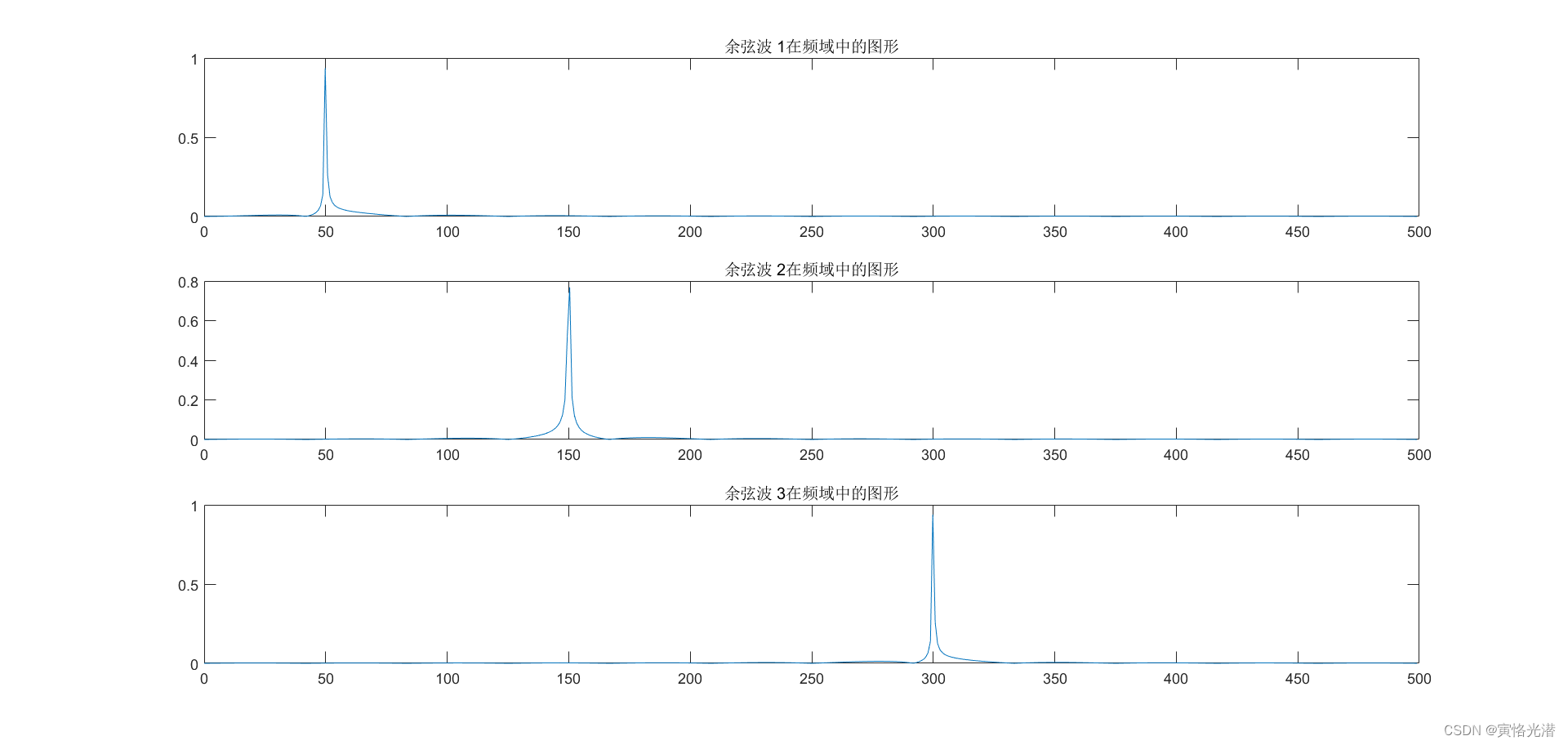
我们可以看到,时域转换到频域之后,问题就变得简单清晰了,当然最后的三个余弦波我们可以使用第一种噪声的方法,三者相加,然后时域转频域,对比发现在时域中信号比较难处理,变换到频域中就变得简单了。
傅里叶变换的余弦波
相关文章:

MATLAB图解傅里叶变换(初学者也可以理解)
1、概述 相信很多人对于傅里叶变换可能觉得比较复杂和有点难懂,其实不难,它只是一种积分变换。 傅里叶变换,表示能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。也就是说&qu…...

uni-app 用于开发H5项目展示饼图,使用ucharts 饼图示例
先下载ucharts H5示例源码: uCharts: 高性能跨平台图表库,支持H5、APP、小程序(微信小程序、支付宝小程序、钉钉小程序、百度小程序、头条小程序、QQ小程序、快手小程序、360小程序)、Vue、Taro等更多支持canvas的框架平台&#…...
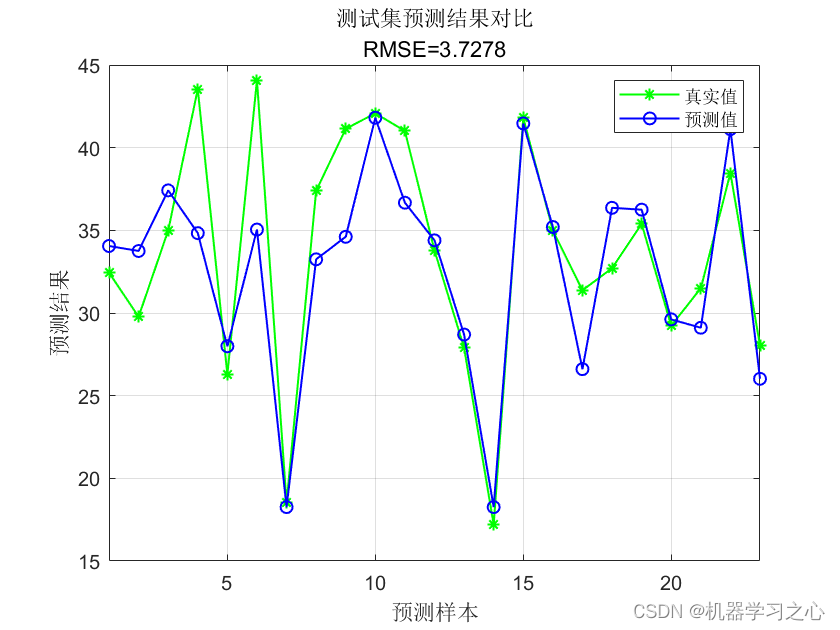
回归预测 | MATLAB实现SABO-LSTM基于减法平均优化器优化长短期记忆神经网络的多输入单输出数据回归预测模型 (多指标,多图)
回归预测 | MATLAB实现SABO-LSTM基于减法平均优化器优化长短期记忆神经网络的多输入单输出数据回归预测模型 (多指标,多图) 目录 回归预测 | MATLAB实现SABO-LSTM基于减法平均优化器优化长短期记忆神经网络的多输入单输出数据回归预测模型 &a…...
JDK bug:ciObjectFactory::create_new_metadata
文章目录 1、问题2.详细日志3.JDK:bug最终bug链接: 京东遇到过类似bug各位大佬如果有更详细的解答可以留言。 1、问题 Problematic frame: V [libjvm.so0x438067] ciObjectFactory::create_new_metadata(Metadata*)0x327 关键字还是ciObjectFactory::cr…...

Flink系列之:Over聚合
Flink系列之:Over聚合 一、Over聚合二、ORDER BY三、PARTITION BY四、范围(RANGE)定义五、RANGE 间隔六、ROW 间隔 适用于流、批 一、Over聚合 OVER 聚合通过排序后的范围数据为每行输入计算出聚合值。和 GROUP BY 聚合不同, OV…...
Java开发工具积累(符合阿里巴巴手册规范)
文章目录 一、命名规约二、代码格式三、集合篇1. 栈、队列、双端队列2. List的升序倒序3. Map的升序降序4. 二维数组排序5. 集合之间的转换6. Map键值对遍历7. 重写equal与hashCode8. ArrayList的subList9. keySet()/values()/ent…...

SiLM5350MDBCA-DG车规级隔离驱动芯片,我们能为汽车智能提供什么?
SiLM5350MDBCA-DG是一款适用于IGBT、MOSFET的单通道 隔离门极驱动器,具有10A拉电流和10A灌电流驱动能 力。提供内部钳位功能,可单独控制 上升时间和下降时间。 在 SOP8 封 装 中 具 有 3000VRMS 隔 离 耐 压 ( 符 合 UL1577)。 与…...

【开题报告】基于SpringBoot的企业财务管理系统的设计与实现
1.研究背景 随着全球经济的发展和市场竞争的加剧,企业财务管理变得越来越重要。企业需要一个高效、精确、安全的财务管理系统来管理企业的财务事务,提供准确的财务数据支持决策制定。传统的手工财务管理方式已经无法满足企业的需求,因此&…...

【C盘清理】Jetbrains全家桶(PyCharm、Clion……)更改 IDE 特定文件(配置、缓存、插件、日志等)存储位置
文章目录 一、官网说明二、更改 IDE 目录的位置1. 转到“帮助”|“编辑自定义属性”2. 各文件位置3. 以PyCharm系统目录为例4. 修改idea.properties 三、清理旧的 IDE 目录 一、官网说明 IDE 使用的目录官网说明 二、更改 IDE 目录的位置 默认情况下,PyCharm 将每…...

nginx部署vue项目
nginx部署vue 解决nginx中vue项目刷新报404问题解决nginx转发后端服务隐藏部分url访问url路径/prod-api/api经过nginx反向代理后,到达后端服务的实际url地址为/api。 解决nginx中vue项目刷新报404问题 location / { …...
Relocations for this machine are not implemented,IDA版本过低导致生成汇编代码失败
目录 1、问题描述 2、安卓app发生崩溃,需要查看汇编代码上下文去辅助分析 3、使用IDA打开.so动态库文件,提示Relocations for this machine are not implemented 4、IDA版本较老,不支持ARM64的指令集,使用7.0版本就可以了 5、…...

[ CTF ]【天格】战队WriteUp-第七届“强网杯”全国安全挑战赛
第七届“强网杯”全国安全挑战赛 2023.12.16~2023.12.17 文章目录 【Misc】Pyjail ! Its myFILTER !!!easyfuzz谍影重重2.0签到Pyjail ! Its myRevenge !!!server_8F6C72124774022B.py 问卷调查 【Reverse】ezre 【Web】happygame 【强网先锋】石头剪刀布TrieSpeedUpezreez_fmt…...
Android13音频录制适配
Android13音频录制适配 前言: 之前写过一篇音频录制的文章,当时是在Android10以下的手机可以成功录制和播放,但是Android10及以上手机提示创建文件失败,最近做过Android13的适配,索性一起把之前的录音也适配了&#…...

【Python】—— 如果使用matplotlib做数据可视化
matplotlib做数据可视化 相关知识掌握matplotlib的基本使用方法1. 折线图2. 散点图3. 柱状图4. 饼图5. 直方图6. 等高线图7. 图形定制 掌握数据处理的基本方法1. 数据筛选2. 缺失值处理3. 异常值处理 理解数据可视化的原则和方法1. 选择合适的图表类型2. 避免数据混淆3. 突出重…...
,高版本多支持))
【MyBatis-Plus】多数据源分页配置(低版本暂时就支持一种(可选),高版本多支持)
【转载】一、Mybatis Plus 3.4 版本之后分页插件的变化 1、地址 Mybatis Plus 3.4版本之后分页插件的变化 2、内容 1、MybatisPlusInterceptor 从 Mybatis Plus 3.4.0 版本开始,不再使用旧版本的 PaginationInterceptor,而是使用 MybatisPlusInterce…...

Linux 特殊符号
目录 1. # 注释 2. ;命令分隔符 3. .. 上级目录 4. . 当前目录 5. " " 换行,解析变量 6. 换行,不解析变量 7. \ 和 / 8. !历史命令调用,取反 9. * 通配符 10. $ 调用变量 11. | 管道 12. || …...

TDengine 签约中船九院,助力航运业智能化转型升级
在大数据时代背景下,船舶智能化已经成为船舶制造与航运领域发展的必然趋势。智能船舶作为《中国制造 2025》中明确重点发展的领域,代表了船舶未来的方向,对于航运业的转型升级至关重要。其中,大数据的处理和运用成为船舶智能化转型…...
upload-labs笔记
简介 upload-labs是一个使用php语言编写的,专门收集渗透测试和CTF中遇到的各种上传漏洞的靶场。旨在帮助大家对上传漏洞有一个全面的了解。目前一共21关,每一关都包含着不同上传方式。 文件上传漏洞是指: Web 服务器允许用户将文件上传至其…...
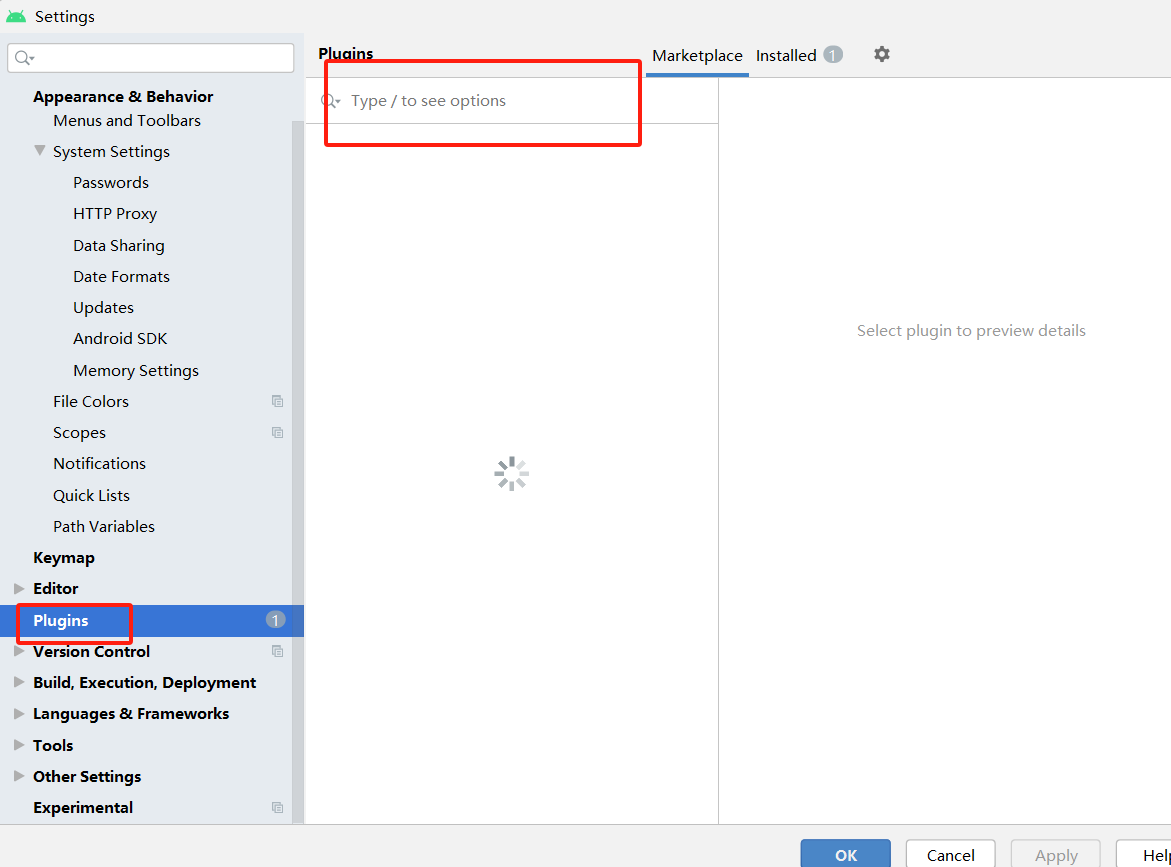
Android Studio好用的插件推荐
目录 一、插件推荐 二、如何下载 1.点击File—>Settings 2.点击Plugins然后进行搜索下载 三、Android Studio 模板 一、插件推荐 这个插件可以为您自动生成Parcelable代码。Parcelable是一种用于在Android组件之间传递自定义对象的机制,但手动编写Parcela…...

第三十九章 其他特殊主题 - 映射 IRIS ID 以供导出
文章目录 第三十九章 其他特殊主题 - 映射 IRIS ID 以供导出控制导出时的命名空间前缀XMLPREFIX 第三十九章 其他特殊主题 - 映射 IRIS ID 以供导出 当在顶层映射 IRIS 对象(而不是作为另一个对象的属性)时,其内部 ID、OID 和全局唯一 ID 不…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...
