【1.8计算机组成与体系结构】磁盘管理
目录
- 1.磁盘基本结构与存取过程
- 1.1 磁盘基本结构
- 1.2 磁盘的存取过程
- 2.磁盘优化分布存储
- 3.磁盘单缓冲区与双缓冲区
- 4.磁盘移臂调度算法
1.磁盘基本结构与存取过程
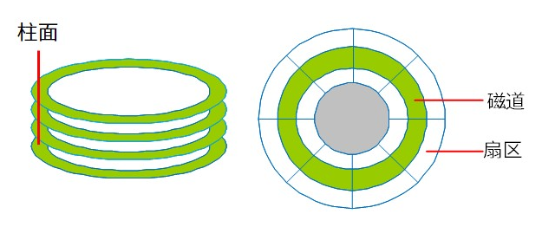
1.1 磁盘基本结构
磁盘:柱面,磁道,扇区。
1.2 磁盘的存取过程
存取时间=寻道时间+等待时间,寻道时间是指磁头移动到磁道所需的时间;等待时间为等待读写的扇区转到磁头下方所用的时间。
🟢读取磁盘数据的时间应包括以下三个部分
(1) 找磁道的时间。
(2) 找块 (扇区) 的时间,即旋转延迟时间。
(3) 传输时间。
🟠平均存取时间 (Average Access Time) ,是指磁头找到指定数据的平均时间。
平均存取时间是指磁头找到指定数据的平均时间,通常它是硬盘平均寻道时间和平均潜伏时间 (等待时间)之和。平均存取时间最能代表硬盘找到某一数据所用的时间,数值越小越好。
🟠平均访问时间=平均寻道时间+平均等待时间
例题:

解析:选D
((10*10)+100+2 )*100=20200
2.磁盘优化分布存储
原本顺序的存储会有一个处理时间,如果没有处理完就紧接着继续读取会再经过一轮的等待时间。
磁盘优化分布存储就是将磁道的物理块位置进行优化,能处理完一个物理块之后紧接着处理下一个物理块。
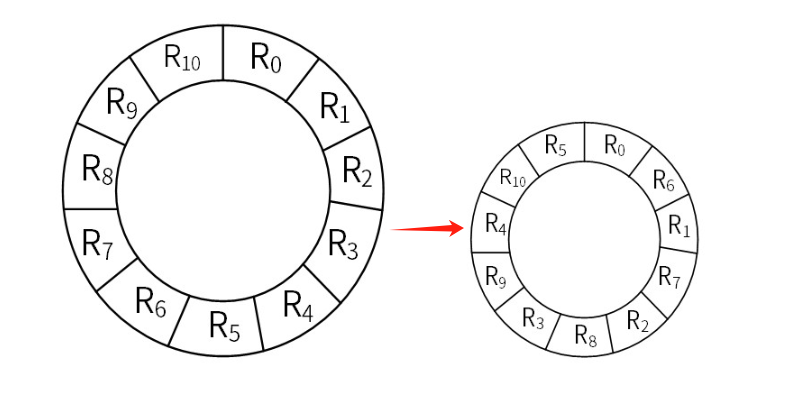
例题:
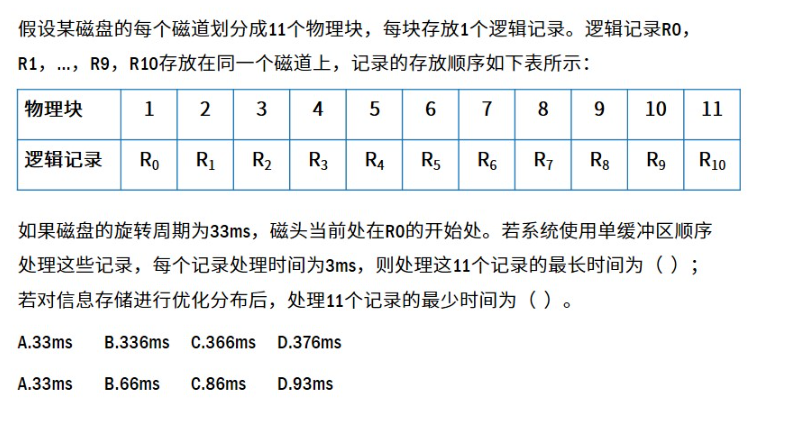
解析:
第一问选C(3*10+3+3)*10+3+3=366
第二问选B(3+3)*11=66
3.磁盘单缓冲区与双缓冲区
双缓冲区:
可以实现读入到缓冲区2和从缓冲区1读入到用户区的并发。读入缓冲区,和从缓冲区读入用户区,可以对不同的缓冲区进行,也就是说,可以并行处理。
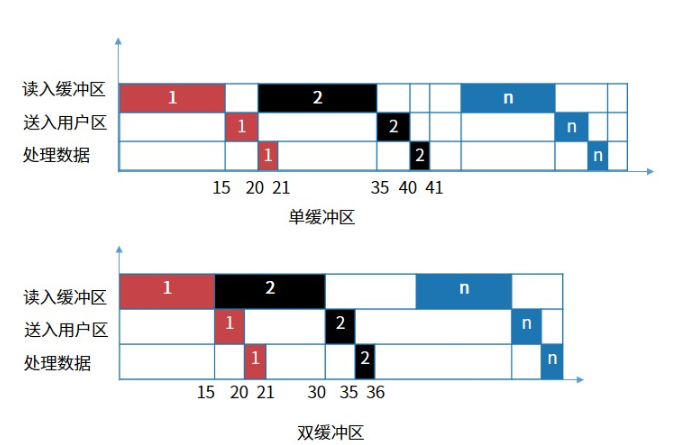
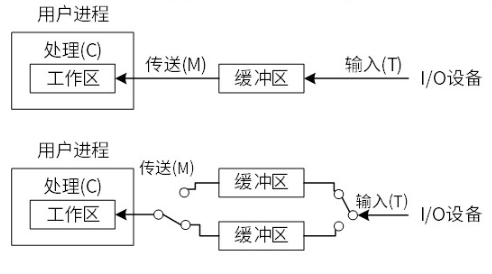
例题:

解析:单缓冲区(读取和送至可以理解为一块)
第一问选D:根据流水线计算公式20+1+(10-1)X20=201。
第二问选C:根据流水线计算公式15+5+1+(10-1)X15=156
4.磁盘移臂调度算法
√ 先来先服务 (FCFS):最早提出的I/O请求首先被服务,然后是后续的请求。
√ 最短寻道时间优先 (SSTF)
√ 扫描算法 (SCAN)
√ 循环扫描(CSCAN) 算法
例题:
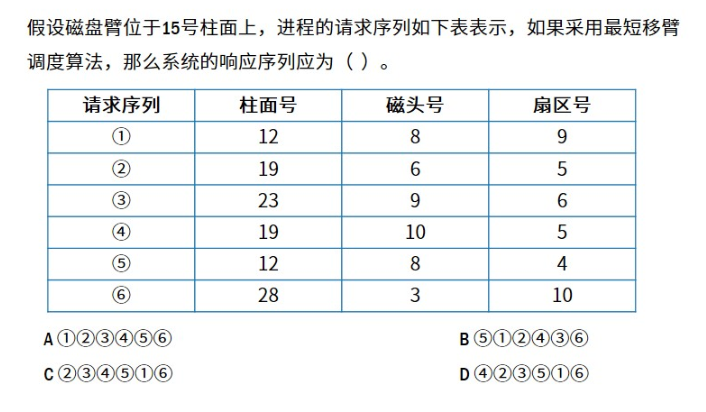
解析:选B;根据最短距离排除15号柱面首选①⑤,A选项的话①之后的顺序应该为⑤故排除。
相关文章:

【1.8计算机组成与体系结构】磁盘管理
目录 1.磁盘基本结构与存取过程1.1 磁盘基本结构1.2 磁盘的存取过程 2.磁盘优化分布存储3.磁盘单缓冲区与双缓冲区4.磁盘移臂调度算法 1.磁盘基本结构与存取过程 1.1 磁盘基本结构 磁盘:柱面,磁道,扇区。 1.2 磁盘的存取过程 存取时间寻…...

1663:【 例 1】取石子游戏 1
【题目描述】 有一种有趣的游戏,玩法如下: 玩家: 2 人; 道具: N 颗石子; 规则: 1、游戏双方轮流取石子; 2、每人每次取走若干颗石子(最少取 1 颗,最多取…...

Django去访问web api接口Object of type Session is not JSON serializable
解决方案:settings.py中加入 :SESSION_SERIALIZER django.contrib.sessions.serializers.PickleSerializer 事由:Django去访问一个web api接口,两次连接之间需要通过Session()保持身份验证。 def sendCode(request): mobile jso…...
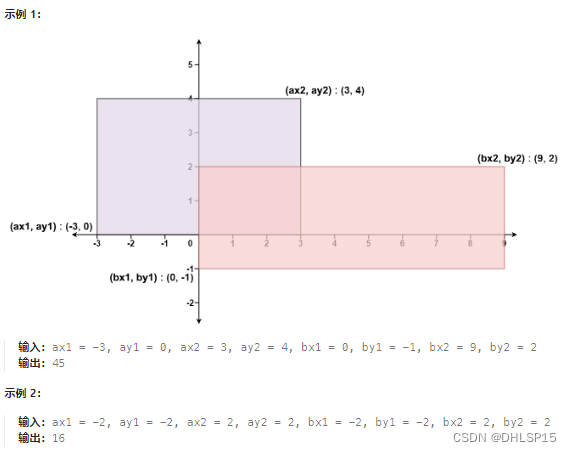
每日一题,二维平面
给你 二维 平面上两个 由直线构成且边与坐标轴平行/垂直 的矩形,请你计算并返回两个矩形覆盖的总面积。 每个矩形由其 左下 顶点和 右上 顶点坐标表示: 第一个矩形由其左下顶点 (ax1, ay1) 和右上顶点 (ax2, ay2) 定义。 第二个矩形由其左下顶点 (bx1, …...

【jupyter notebook】jupyter notebook 调用另一个jupyter notebook 的函数
总结 使用 %run 魔法命令将 Notebook 转换为py文件使用 nbimporter 库手动复制代码优点notebook最前面加上即可最基本方法就跟导入py文件一样,不会被执行一遍快缺点所有的代码都会执行一遍修改原文件就要重新转换,且 从自定义的 .py 文件中导入函数时&a…...

Linux--学习记录(3)
G重要编译参数 -g(GDB调试) -g选项告诉gcc产生能被GNU调试器GDB使用的调试信息,以调试程序编译带调试信息的可执行文件g -g hello.c -o hello编译过程: -E(预处理) g -E hello.c -o hello.i-S(编…...
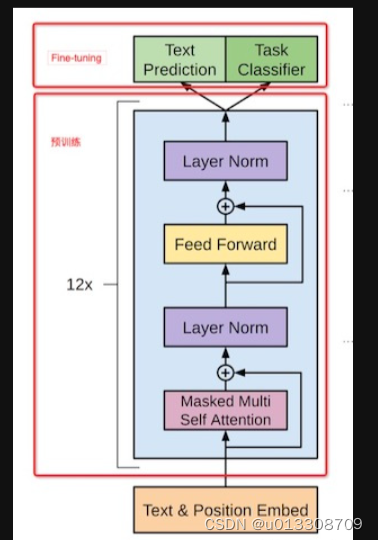
自然语言处理阅读第一弹
Transformer架构 encoder和decoder区别 Embeddings from Language Model (ELMO) 一种基于上下文的预训练模型,用于生成具有语境的词向量。原理讲解ELMO中的几个问题 Bidirectional Encoder Representations from Transformers (BERT) BERT就是原生transformer中的Encoder两…...

Spring Boot+Mybatis设置sql日志打印
在全局配置文件添加以下内容:logging.level.com.demo.mapperdebug,com.demo.mapper:src下的mapper路径,debug:设置日志打印级别为debug,亦可设置为:ERROR、WARN、INFO application.properties …...

步进电机电流设置的3种方法
本文介绍步进电机电流设置的3种方法。 步进电机电流设置包括运行电流(IRun)和保持电流(IHold)2种。电机运行时需要有较大电流以保证有足够的力矩使物体运动,而停止的时候,为了减少电机发热及降低功耗&…...

uniapp-使用返回的base64转换成图片
在实际开发的时候 需要后端实时的给我返回二维码 他给我返回的是加密后的base64字符串 我需要利用这个base64转换到canvas画布上展示 或者以图片的形式展示在页面内 在canvas画布上展示 使用官方的uni.getFileSystemManager().writeFile()方法可将base64码转成的二维码显示在…...

有机面条市场分析:到2026 年的复合年增长率为 5.4%
近年来,有机面条因其健康益处和可持续性而广受欢迎。由于消费者对健康和天然食品的需求不断增加,预计 全球有机面条市场将继续以显着速度增长。特别是中国市场,由于健康意识的提高以及对有机和天然产品的兴趣 增加,有机面条消费量…...

广州设计周落幕|值得被歌颂的奥力斯特岩板
12月11日,一年一度的广州设计周,为期四天的展会在广州保利世贸博览馆、广州国际采购中心和南丰国际会展中心三大展馆已落下帷幕。依旧熙攘,依旧热烈,远道而来的专家领导、媒体嘉宾、展商代表、外国友人、设计爱好者,风…...

WTN6系列语音芯片:PWM与DAC音频输出在PCB设计中的优势
随着科技的飞速发展,语音芯片在电子产品中的应用越来越广泛。其中,唯创知音的WTN6系列语音芯片凭借其卓越的性能和多样的功能,受到了市场的热烈欢迎。特别是其支持PWM和DAC两种音频输出方式的特点,使得工程师在PCB设计时能够更加灵…...
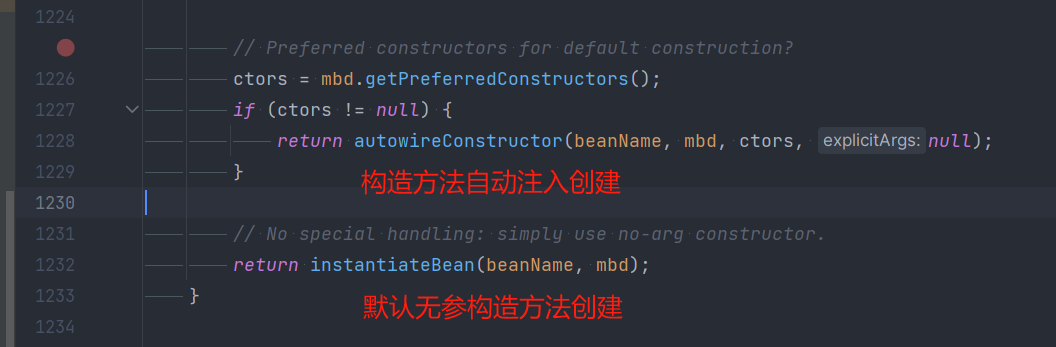
设计模式 原型模式 与 Spring 原型模式源码解析(包含Bean的创建过程)
原型模式 原型模式(Prototype模式)是指:用原型实例指定创建对象的种类,并且通过拷贝这些原型,创建新的对象。 原型模式是一种创建型设计模式,允许一个对象再创建另外一个可定制的对象,无需知道如何创建的细节。 工作原…...
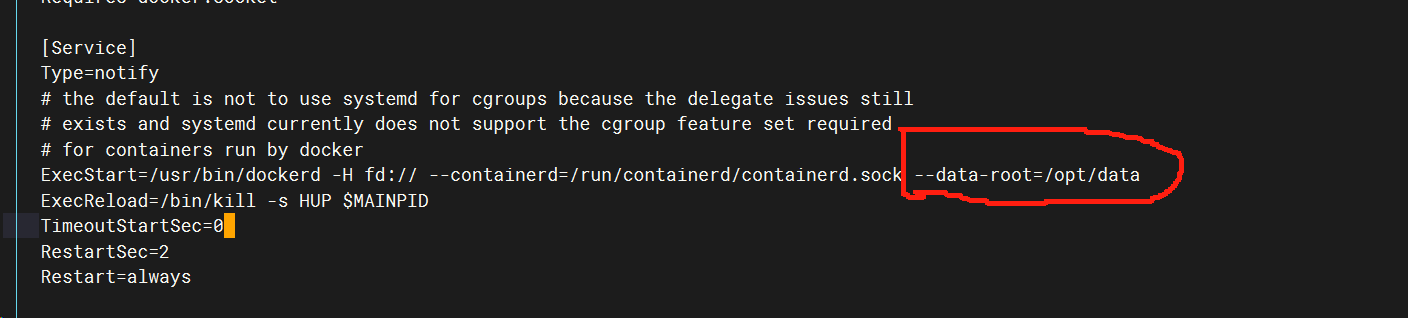
Docker介绍,Docker安装
docker镜像仓库官网 一、Docker的基本概念 1.Docker的三大核心组件 docker 镜像 --------docker images docker 仓库---------docker registeries docker 容器---------docker containers 2.Docker 镜像 Docker镜像是运行docker容器时的只读模板,每一个镜像由一…...
CLIP 对比学习 源码理解快速学习
最快的学习方法,理清思路,找视频讲解,看源码逻辑: CLIP 源码讲解 唐宇 输入: 图像-文本成对配对的数据 训练模型的过程(自己理解): 怎么做的?:利用数据内部…...
6.鸿蒙app_hap_DevEco如何真机调试模式_app安装在手机中
真机调试 手机》设置》关于手机》HarmonyOS版本》软件版本,连续单击10次启动开发者模式 然后:设置》系统和更新》开发人员选项》打开USB调试功能。 电脑USB连接手机,手机USB连接类型,传文件(不要选择仅充电…...
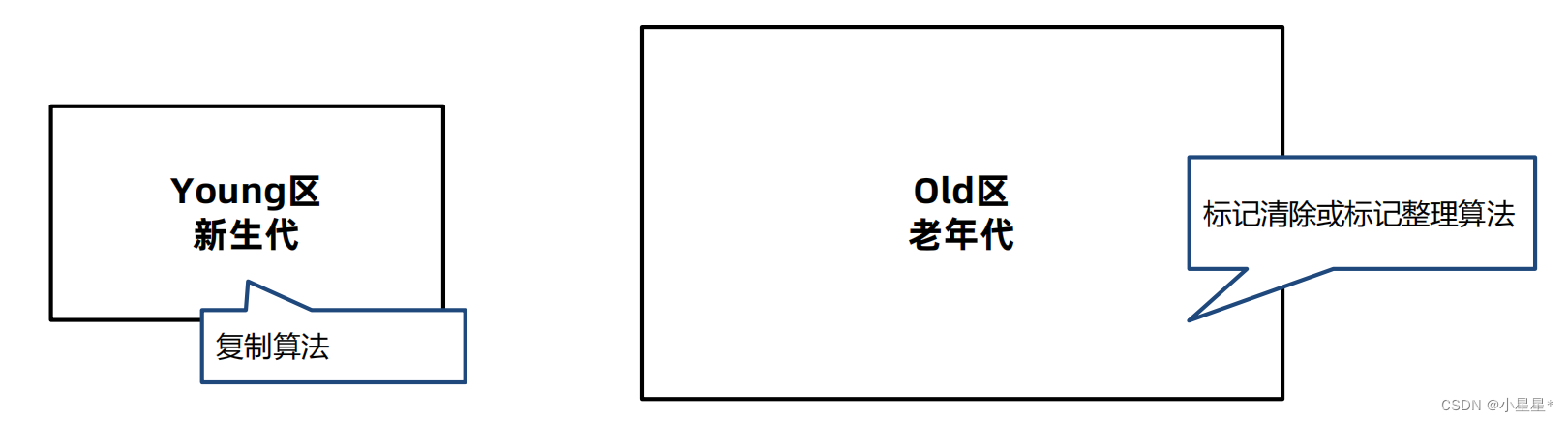
【JVM从入门到实战】(八)垃圾回收(1)
内存泄漏:指的是不再使用的对象在系统中未被回收,内存泄漏的积累可能会导致内存溢出 什么是垃圾回收 Java中为了简化对象的释放,引入了自动的垃圾回收(Garbage Collection简称GC)机制。通过垃 圾回收器来对不再使用的…...
-删除有序数组中的重复项)
LeeCode前端算法基础100题(12)-删除有序数组中的重复项
一、问题详情: 给你一个 非严格递增排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。 考虑 nums 的唯一元素的数量为 k ,你需要做以下事情确保你的题…...
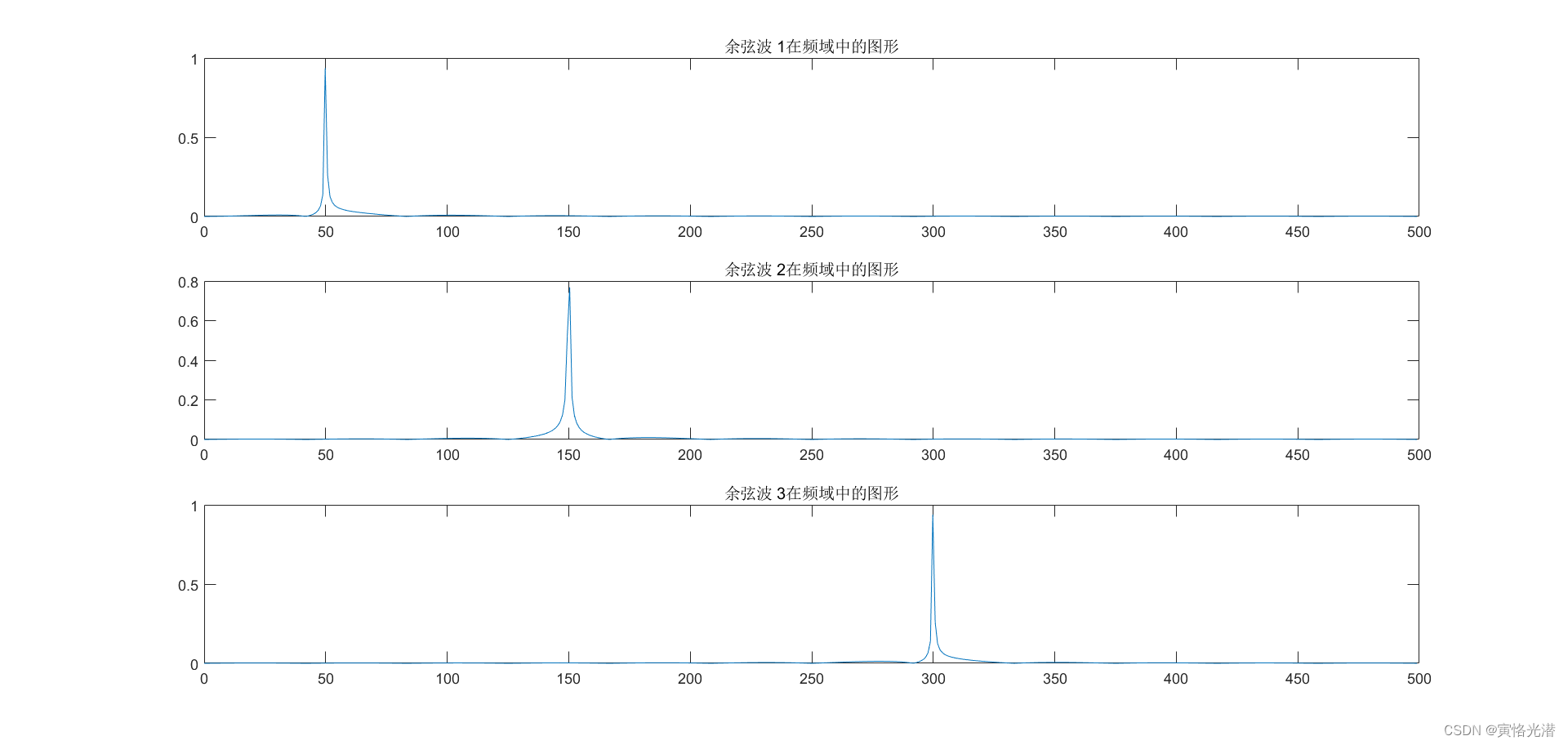
MATLAB图解傅里叶变换(初学者也可以理解)
1、概述 相信很多人对于傅里叶变换可能觉得比较复杂和有点难懂,其实不难,它只是一种积分变换。 傅里叶变换,表示能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。也就是说&qu…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...
