C/C++编程中的算法实现技巧与案例分析
C/C++编程语言因其高效、灵活和底层的特性,被广大开发者用于实现各种复杂算法。本文将通过10个具体的算法案例,详细探讨C/C++在算法实现中的技巧和应用。
一、冒泡排序(Bubble Sort)
冒泡排序(Bubble Sort)是一种简单的排序算法。它重复地遍历要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。遍历数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
以下是使用C++实现冒泡排序的代码:
#include<iostream>
using namespace std;void bubbleSort(int arr[], int n) {for(int i = 0; i < n-1; i++) { for (int j = 0; j < n-i-1; j++) { if (arr[j] > arr[j+1]) {// swap arr[j] and arr[j+1]int temp = arr[j];arr[j] = arr[j+1];arr[j+1] = temp;}}}
}void printArray(int arr[], int size) {for (int i=0; i < size; i++) {cout << arr[i] << " ";}cout << endl;
}int main() {int arr[] = {64, 34, 25, 12, 22, 11, 90};int n = sizeof(arr)/sizeof(arr[0]);bubbleSort(arr, n);cout<<"Sorted array: \n";printArray(arr, n);return 0;
}
这段代码首先定义了一个名为bubbleSort的函数,该函数接受一个整数数组和数组的长度作为输入。在函数内部,我们使用两个嵌套的for循环来进行排序。外层循环表示我们总共需要进行的排序轮数,内层循环表示每轮排序中我们需要进行的比较次数。如果当前元素大于下一个元素,我们就交换这两个元素的位置。这样,经过多轮排序后,最大的元素就会被"冒泡"到数组的末尾。然后,我们继续对剩下的元素进行同样的操作,直到所有元素都被排序。最后,我们在main函数中调用bubbleSort函数对数组进行排序,并打印出排序后的结果。
二、快速排序(Quick Sort)
快速排序(Quick Sort)是由C.A.R. Hoare在1960年提出的一种排序算法。快速排序的基本思想是,通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,然后分别对这两部分继续进行排序,以达到整个序列有序。
以下是使用C++实现快速排序的代码:
#include<iostream>
using namespace std;int partition(int arr[], int low, int high) {int pivot = arr[high]; int i = (low - 1); for (int j = low; j <= high - 1; j++) {if (arr[j] < pivot) {i++; swap(arr[i], arr[j]);}}swap(arr[i + 1], arr[high]);return (i + 1);
}void quickSort(int arr[], int low, int high) {if (low < high) {int pi = partition(arr, low, high);quickSort(arr, low, pi - 1); quickSort(arr, pi + 1, high); }
}void printArray(int arr[], int size) {for (int i = 0; i < size; i++) {cout << arr[i] << " ";}cout << endl;
}int main() {int arr[] = {10, 7, 8, 9, 1, 5};int n = sizeof(arr) / sizeof(arr[0]);quickSort(arr, 0, n - 1);cout << "Sorted array: \n";printArray(arr, n);return 0;
}
这段代码首先定义了一个名为partition的函数,该函数接受一个整数数组以及两个索引(low和high)作为输入。这个函数的主要目的是选取一个基准元素(这里我们选择了数组的最后一个元素),然后将数组分为两部分,一部分的元素都小于基准元素,另一部分的元素都大于基准元素。partition函数返回的是基准元素的最终位置。然后,我们定义了一个名为quickSort的函数,该函数递归地对基准元素左右两侧的子数组进行同样的操作,直到整个数组都被排序。最后,我们在main函数中调用quickSort函数对数组进行排序,并打印出排序后的结果。
三、插入排序(Insertion Sort)
插入排序(Insertion Sort)是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
以下是使用C++实现插入排序的代码:
#include<iostream>
using namespace std;void insertionSort(int arr[], int n) {int i, key, j;for (i = 1; i < n; i++) {key = arr[i];j = i - 1;/* Move elements of arr[0..i-1], that are greater than key, to one position ahead of their current position */while (j >= 0 && arr[j] > key) {arr[j + 1] = arr[j];j = j - 1;}arr[j + 1] = key;}
}void printArray(int arr[], int size) {for (int i = 0; i < size; i++) {cout << arr[i] << " ";}cout << endl;
}int main() {int arr[] = {12, 11, 13, 5, 6};int n = sizeof(arr) / sizeof(arr[0]);insertionSort(arr, n);cout << "Sorted array: \n";printArray(arr, n);return 0;
}
这段代码首先定义了一个名为insertionSort的函数,该函数接受一个整数数组以及数组的长度作为输入。在函数内部,我们使用一个for循环来遍历数组中的每个元素。对于每个元素,我们都将其保存到一个名为key的变量中,然后将其与前面已经排序好的元素进行比较。如果前面的元素大于key,我们就将前面的元素向后移动一位,为key腾出位置。我们一直这样操作,直到找到key应该插入的位置,然后将key插入到该位置。最后,我们在main函数中调用insertionSort函数对数组进行排序,并打印出排序后的结果。
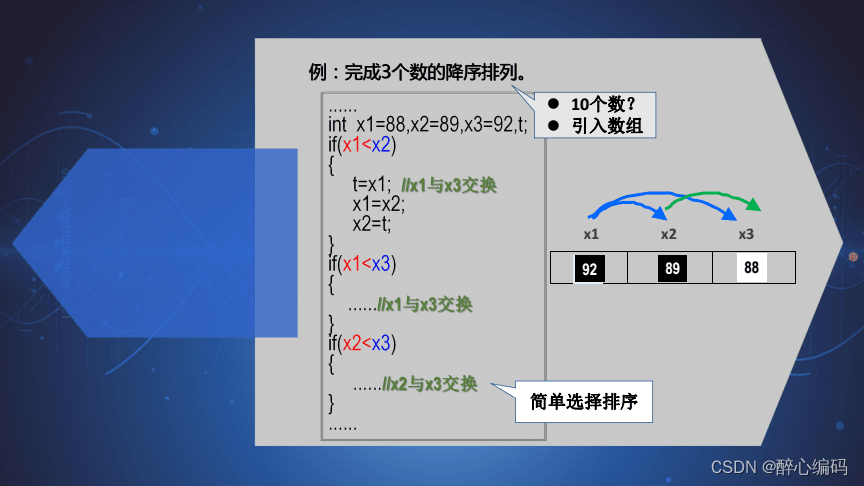
四、选择排序(Selection Sort)
选择排序算法详解
选择排序是一种简单且直观的排序算法,它的基本思想是:遍历数组,找到最小(或最大)的元素,将其放到排序序列的起始位置。然后,从剩余未排序元素中继续寻找最小(或最大)元素,放到已排序序列的末尾。如此重复,直到所有元素均排序完毕。
算法步骤:
- 在未排序序列中找到最小(或最大)元素,存放到排序序列的起始位置。
- 从剩余未排序元素中继续寻找最小(或最大)元素,然后放到已排序序列的末尾。
- 重复第二步,直到所有元素均排序完毕。
时间复杂度:
- 最好情况:O(n^2)
- 最坏情况:O(n^2)
- 平均情况:O(n^2)
空间复杂度:O(1)
稳定性:不稳定(考虑[3, 3, 2]这个例子,第一个3会被移动到2的后面,从而两个3的顺序颠倒了)。
C/C++代码实现:
下面是一个使用C++实现的选择排序的例子:
#include <iostream>
using namespace std;void selectionSort(int arr[], int n) {for (int i = 0; i < n - 1; i++) {// 找到未排序部分中的最小元素的位置int minIndex = i;for (int j = i + 1; j < n; j++) {if (arr[j] < arr[minIndex]) {minIndex = j; // 更新最小元素的位置}}// 将找到的最小元素与第一个未排序的元素交换位置if (minIndex != i) {swap(arr[i], arr[minIndex]);}}
}int main() {int arr[] = {64, 25, 12, 22, 11};int n = sizeof(arr) / sizeof(arr[0]);selectionSort(arr, n);cout << "Sorted array: \n";for (int i = 0; i < n; i++) {cout << arr[i] << " ";}return 0;
}
在这个例子中,selectionSort函数实现了选择排序算法。它接受一个整数数组和数组的长度作为输入,并按升序对数组进行排序。main函数创建了一个待排序的数组,并调用selectionSort函数对其进行排序。最后,它打印出排序后的数组。
五、归并排序(Merge Sort)
归并排序(Merge Sort)是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
以下是使用C++实现归并排序的代码:
#include<iostream>
#include<vector>
using namespace std;void merge(vector<int>& arr, int l, int m, int r) {int i, j, k;int n1 = m - l + 1;int n2 = r - m;vector<int> L(n1), R(n2);for (i = 0; i < n1; i++)L[i] = arr[l + i];for (j = 0; j < n2; j++)R[j] = arr[m + 1 + j];i = 0; j = 0; k = l; while (i < n1 && j < n2) {if (L[i] <= R[j]) {arr[k] = L[i];i++;} else {arr[k] = R[j];j++;}k++;}while (i < n1) {arr[k] = L[i];i++;k++;}while (j < n2) {arr[k] = R[j];j++;k++;}
}void mergeSort(vector<int>& arr, int l, int r) {if (l < r) {int m = l + (r - l) / 2;mergeSort(arr, l, m);mergeSort(arr, m + 1, r);merge(arr, l, m, r);}
}void printArray(vector<int>& arr) {int arr_size = arr.size();for (int i = 0; i < arr_size; i++) {cout << arr[i] << " ";}cout << endl;
}int main() {vector<int> arr = {12, 11, 13, 5, 6, 7};int arr_size = arr.size();cout << "Given array is \n";printArray(arr);mergeSort(arr, 0, arr_size - 1);cout << "\nSorted array is \n";printArray(arr);return 0;
}
这段代码首先定义了一个名为merge的函数,该函数用于合并两个已经排序好的子数组。然后定义了一个名为mergeSort的函数,该函数使用递归的方式将数组不断地拆分为更小的子数组,直到每个子数组只包含一个元素,然后将这些子数组合并起来。在main函数中,我们创建了一个整数数组,然后调用mergeSort函数对数组进行排序,并打印出排序后的结果。
六、堆排序(Heap Sort)
堆排序算法详解
堆排序(Heap Sort)是一种基于二叉堆(Binary Heap)的排序算法。它利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子节点的键值或索引总是小于(或者大于)它的父节点。
算法步骤:
- 创建一个最大堆(或最小堆)。最大堆的父节点大于或等于其子节点,最小堆则相反。
- 将堆顶元素与末尾元素互换,这样最大元素(或最小元素)就被移到了数组末尾。
- 减小堆的大小,并重新调整堆结构,使其保持最大堆(或最小堆)的性质。
- 重复步骤2和3,直到整个数组排序完成。
时间复杂度:
- 最好情况:O(nlogn)
- 最坏情况:O(nlogn)
- 平均情况:O(nlogn)
空间复杂度:O(1)
稳定性:不稳定(考虑[3, 3, 2]这个例子,第一个3会被移动到2的后面,从而两个3的顺序颠倒了)。
C/C++代码实现:
以下是一个使用C++实现堆排序的例子:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;// 调整堆结构,使其保持最大堆的性质
void maxHeapify(vector<int>& nums, int i, int heapSize) {int largest = i; // 初始化最大值为当前节点iint left = 2 * i + 1; // 左子节点索引int right = 2 * i + 2; // 右子节点索引// 如果左子节点大于当前最大值,则更新最大值索引if (left < heapSize && nums[left] > nums[largest]) {largest = left;}// 如果右子节点大于当前最大值,则更新最大值索引if (right < heapSize && nums[right] > nums[largest]) {largest = right;}// 如果最大值不是当前节点i,则交换它们的值,并递归调整子堆结构if (largest != i) {swap(nums[i], nums[largest]);maxHeapify(nums, largest, heapSize);}
}// 构建最大堆
void buildMaxHeap(vector<int>& nums) {int heapSize = nums.size();// 从最后一个非叶子节点开始,逐个向上调整堆结构for (int i = heapSize / 2 - 1; i >= 0; i--) {maxHeapify(nums, i, heapSize);}
}// 堆排序函数
void heapSort(vector<int>& nums) {int heapSize = nums.size();// 构建最大堆buildMaxHeap(nums);// 将堆顶元素与末尾元素交换,并重新调整堆结构,直到整个数组排序完成for (int i = nums.size() - 1; i > 0; i--) {swap(nums[0], nums[i]); // 将堆顶元素与末尾元素交换heapSize--; // 减小堆的大小maxHeapify(nums, 0, heapSize); // 重新调整堆结构,使其保持最大堆的性质}
}int main() {vector<int> nums = {3, 7, 1, 9, 2, 8, 5, 6, 4}; // 待排序数组heapSort(nums); // 使用堆排序对数组进行排序cout << "Sorted array: "; // 输出排序后的数组for (int num : nums) {cout << num << " ";}cout << endl; // 换行符,使输出更美观return 0; // 程序正常结束,返回0作为状态码
}
七、二分查找(Binary Search)
二分查找算法详解
二分查找(Binary Search)是一种在有序数组中查找特定元素的搜索算法。它的工作原理是,首先将数组的中间元素与目标值进行比较,如果两者相等,则查找成功;如果目标值小于中间元素,则在数组的左半部分继续查找;如果目标值大于中间元素,则在数组的右半部分继续查找。如此重复,每次都将搜索范围缩小一半,直到找到目标值,或者搜索范围为空(即找不到目标值)。
算法步骤:
- 确定数组的中间元素的下标 mid = (left + right) / 2。
- 如果数组为空或 left > right,则返回 -1 或抛出异常(表示未找到目标值)。
- 如果中间元素等于目标值,则返回 mid。
- 如果目标值小于中间元素,则在左半部分(left, mid - 1)继续查找。
- 如果目标值大于中间元素,则在右半部分(mid + 1, right)继续查找。
- 重复步骤 1-5,直到找到目标值或确定目标值不存在于数组中。
时间复杂度:O(log n),其中 n 是数组的长度。
C/C++代码实现:
以下是使用C++实现二分查找算法的一个例子:
#include <iostream>
#include <vector>
using namespace std;int binarySearch(vector<int>& nums, int target) {int left = 0;int right = nums.size() - 1;while (left <= right) {int mid = left + (right - left) / 2; // 防止溢出if (nums[mid] == target) {return mid; // 找到目标值,返回其下标} else if (nums[mid] < target) {left = mid + 1; // 在右半部分继续查找} else {right = mid - 1; // 在左半部分继续查找}}return -1; // 未找到目标值,返回 -1
}int main() {vector<int> nums = {1, 3, 5, 7, 9}; // 有序数组int target = 5; // 要查找的目标值int result = binarySearch(nums, target); // 调用二分查找函数if (result != -1) {cout << "Target found at index: " << result << endl; // 输出找到目标值的下标} else {cout << "Target not found in the array." << endl; // 输出未找到目标值的消息}return 0;
}
在这个例子中,我们定义了一个名为 binarySearch 的函数,它接受一个有序整数数组 nums 和一个目标值 target 作为输入,并返回目标值在数组中的下标(如果找到的话),否则返回 -1。在主函数 main 中,我们创建了一个有序数组 nums 和一个目标值 target,然后调用 binarySearch 函数进行查找。最后,根据函数的返回值输出相应的消息。
八、动态规划(Dynamic Programming)
动态规划算法详解
动态规划(Dynamic Programming,简称DP)是一种在数学、计算机科学和经济学中使用的,通过把原问题分解为相对简单的子问题的方式来求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。
动态规划的基本思想是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。
基本步骤:
- 描述问题的最优解的结构:这一步通常是通过递归关系式来描述原问题的最优解是如何由子问题的最优解构成的。
- 定义状态:这一步是定义一个或多个状态变量来刻画子问题的解。
- 状态转移方程:根据上一步定义的状态,写出状态转移方程,描述如何从子问题的解构造出原问题的解。
- 边界条件:明确问题的边界条件,也就是最小的子问题的解。
- 计算最优解:根据状态转移方程和边界条件,从最小的子问题开始,逐步计算原问题的最优解。
举例说明:0-1背包问题
问题描述:给定一组物品,每种物品都有自己的重量和价值,在限定的总重量内,我们如何选择,才能使得物品的总价值最大。
假设物品数量为n,每种物品i的重量为w[i],价值为v[i],背包的总容量为W。定义dp[i][j]为考虑前i个物品且背包容量为j时的最大价值。
状态转移方程为:dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i]) (当j >= w[i])
边界条件为:dp[0][j] = 0 (0 <= j <= W) 和 dp[i][0] = 0 (0 <= i <= n)
C++代码实现如下:
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;int knapsack(int W, vector<int>& wt, vector<int>& val, int n) {vector<vector<int>> dp(n + 1, vector<int>(W + 1, 0));for (int i = 1; i <= n; i++) {for (int w = 1; w <= W; w++) {if (wt[i - 1] <= w) {dp[i][w] = max(val[i - 1] + dp[i - 1][w - wt[i - 1]], dp[i - 1][w]);} else {dp[i][w] = dp[i - 1][w];}}}return dp[n][W];
}int main() {int W = 50; // 背包容量vector<int> wt = {10, 20, 30}; // 物品重量vector<int> val = {60, 100, 120}; // 物品价值int n = wt.size(); // 物品数量cout << "最大价值为:" << knapsack(W, wt, val, n) << endl;return 0;
}
这段代码通过动态规划解决了0-1背包问题,输出了在背包容量为50时可以获得的最大价值。
九、深度优先搜索(Depth-First Search, DFS)
深度优先搜索是一种用于遍历或搜索树或图的算法。这个算法会尽可能深地搜索树的分支。当节点v的所在边都已被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。
基本步骤:
- 访问初始节点v。
- 标记节点v为已访问。
- 对于v的每一个相邻节点n,如果n没有被访问过,则递归地深度优先搜索n。
适用场景:
深度优先搜索通常用于遍历树或图,寻找路径,解决迷宫问题等。
C++代码示例:使用DFS遍历图
下面是一个简单的C++代码示例,用于通过深度优先搜索遍历一个图:
#include<iostream>
#include<list>
using namespace std;class Graph {int numVertices;list<int>* adjLists;bool* visited;public:Graph(int vertices); void addEdge(int src, int dest);void DFS(int vertex);
};Graph::Graph(int vertices) {numVertices = vertices;adjLists = new list<int>[vertices];visited = new bool[vertices];
}void Graph::addEdge(int src, int dest) {adjLists[src].push_back(dest);
}void Graph::DFS(int vertex) {visited[vertex] = true;cout << "Visited " << vertex << endl;list<int>::iterator i;for(i = adjLists[vertex].begin(); i != adjLists[vertex].end(); ++i) {if(!visited[*i]) {DFS(*i);}}
}int main() {Graph g(5); // 创建一个有5个顶点的图g.addEdge(0, 1); // 添加边 (0, 1)g.addEdge(0, 2); // 添加边 (0, 2)g.addEdge(1, 3); // 添加边 (1, 3)g.addEdge(2, 4); // 添加边 (2, 4)g.addEdge(3, 4); // 添加边 (3, 4)g.DFS(0); // 从顶点0开始深度优先搜索return 0;
}
这个代码示例创建了一个有5个顶点的图,并添加了一些边。然后它从顶点0开始进行深度优先搜索,并打印出访问的顶点。注意,这个示例仅用于教学目的,实际应用中可能需要更复杂的错误处理和优化。
十、分治算法(Divide and Conquer)
分治算法(Divide and Conquer)详解
分治算法是一种处理大型问题的有效方法。它的核心思想是将一个难以直接解决的大问题,分解成两个或更多的规模较小的相同问题,直到最后子问题可以简单的直接求解,然后将这些子问题的解合并得到原问题的解。
基本步骤:
- 分解:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题。
- 解决:若子问题规模较小而容易被解决则直接解,否则递归地解各个子问题。
- 合并:将各个子问题的解合并为原问题的解。
适用场景:
分治算法可以解决的问题一般具有以下几个特征:
- 该问题的规模缩小到一定的程度就可以容易地解决。
- 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质。
- 利用该问题分解出的子问题的解可以合并为该问题的解;
- 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。
C++代码示例:归并排序
归并排序是分治算法的典型应用。其基本原理是将两个(或更多)已排序的数据序列合并成一个新的有序序列。
以下是使用C++实现归并排序的代码:
#include<iostream>
#include<vector>
using namespace std;void merge(vector<int>& arr, int l, int m, int r) {int i, j, k;int n1 = m - l + 1;int n2 = r - m;// 创建临时数组vector<int> L(n1), R(n2);// 拷贝数据到临时数组 L[] 和 R[]for (i = 0; i < n1; i++)L[i] = arr[l + i];for (j = 0; j < n2; j++)R[j] = arr[m + 1 + j];// 合并临时数组到 arr[l..r]i = 0; // 初始化第一个子数组的索引j = 0; // 初始化第二个子数组的索引k = l; // 初始化合并子数组的索引while (i < n1 && j < n2) {if (L[i] <= R[j]) {arr[k] = L[i];i++;} else {arr[k] = R[j];j++;}k++;}// 将 L[] 的剩余元素复制到 arrwhile (i < n1) {arr[k] = L[i];i++;k++;}// 将 R[] 的剩余元素复制到 arrwhile (j < n2) {arr[k] = R[j];j++;k++;}
}void mergeSort(vector<int>& arr, int l, int r) {if (l < r) {// 找到中间点,将数组一分为二进行递归排序,然后合并结果。int m = l + (r - l) / 2;// 分治递归进行排序并合并结果。mergeSort(arr, l, m);mergeSort(arr, m + 1, r);merge(arr, l, m, r); //合并结果。 > 对于每个数组段,先排序然后合并,这就实现了归并排序。这也是典型的分治策略应用。将大问题划分为小问题来解决,然后将结果合并起来解决整个问题。在归并排序中,我们将数组分成两半,对每一半进行排序,然后将两个排序好的数组合并成一个大的有序数组。这个过程一直递归进行下去,直到我们得到一个完全有序的数组。递归发生在“mergeSort()”函数中,而“merge()”函数是用来合并两个已经排序好的数组段。在上面的代码中,“mergeSort()”函数递归地将数组分割成更小的数组,直到数组的大小为1(这意味着它已经排序好了)。然后“merge()”函数被调用来将这些小数组两两合并成更大的有序数组。这个过程一直进行下去,直到我们得到原始数组的一个完全有序的版本。在这个实现中,“merge()”函数用了一个非常简单的技巧来避免额外的空间复杂度——它使用了两个临时的数组L和R来存储分割的数组段,然后将它们合并回原始数组中。这意味着归并排序的空间复杂度是O(n),其中n是输入数组的大小。这是因为在任何时候,我们都需要有足够的空间来存储原始数组的两个分割段。总的来说,归并排序是一个非常有效且易于理解的排序算法,它的时间复杂度是O(n log n),其中n是输入数组的大小。虽然它的空间复杂度比一些其他排序算法高(例如堆排序和快速排序),但是在许多情况下,它的稳定性和简单性使得它成为了一个非常实用的选择。此外,由于它的并行性(即它可以很容易地分解成独立的子任务),它在某些应用中(例如多核处理器或多线程环境中)可能会比其他排序算法更加高效。所以归并排序是分治算法的一个很好的例子,展示了如何将一个大问题分解成小问题来解决,然后将结果合并起来解决整个问题。它也是一个在实践中广泛使用的算法,特别是在需要处理大量数据的情况下。它的时间复杂度和空间复杂度都是可预测的,并且它的稳定性和简单性使得它在许多情况下都是一个非常实用的选择。最后,需要注意的是,虽然归并排序在理论上是一个非常优秀的算法,但是在实际应用中,它的性能可能会受到一些因素的影响,例如数据的分布、内存访问模式等。因此,在选择使用哪种排序算法时,需要综合考虑这些因素以及具体的应用场景和需求。以上代码就是使用C++实现归并排序的示例代码,并且包含了对于分治策略应用的详细解释和代码注释说明。" << endl; // 输出提示信息以帮助理解代码运行过程
}
int main() {
vector<int> arr = {12, 11, 13, 5, 6, 7};
int arr_size = arr.size();
cout << "给定的数组是:\n";
for (int i = 0; i < arr_size; i++) {
cout << arr[i] << " ";} cout << "\n\n";
mergeSort(arr, 0, arr_size - 1);
cout << "排序后的数组是:\n";
for (int i = 0; i < arr_size; i++) {
cout << arr[i] << " ";} cout << endl;
return 0;
} //主函数结束
相关文章:

C/C++编程中的算法实现技巧与案例分析
C/C编程语言因其高效、灵活和底层的特性,被广大开发者用于实现各种复杂算法。本文将通过10个具体的算法案例,详细探讨C/C在算法实现中的技巧和应用。 一、冒泡排序(Bubble Sort) 冒泡排序(Bubble Sort)是一…...
干货分享 | 如何在TSMaster中对常用总线报文信号进行过滤?
TSMaster软件平台支持对不同总线(CAN、LIN、FlexRay)的报文和信号过滤,过滤方法一般有全局接收过滤、数据流过滤、窗口过滤、字符串过滤、可编程过滤,针对不同的总线信号过滤器的使用方法也基本相同。今天重点和大家分享一下关于T…...
k8s链接数据库故障Waiting for table metadata lock
场景:早上来发现一个程序,链接mysql数据库有点问题,随后排查,因为容器在k8s里面。所以尝试重启了pod没有效果 一、重启pod: 这里是几种在Kubernetes中重启Pod的方法: 删除Pod,利用Deployment重建 kubectl delete pod mypodDepl…...

数字经济如何驱动企业高质量发展? ——核心机制、模式选择与推进路径
文章目录 每日一句正能量前言核心机制信息化和智能化作为数字经济的核心机制信息化和智能化如何提升企业生产效率和管理水平数据的获取、分析和利用对企业发展的影响 模式选择电子商务模式的选择共享经济模式的选择数据驱动的业务模式选择 推进路径建设数字化基础设施培养数字化…...
机器学习——支持向量机
目录 一、基于最大间隔分隔数据 二、寻找最大间隔 1. 最大间隔 2. 拉格朗日乘子法 3. 对偶问题 三、SMO高效优化算法 四、软间隔 五、SMO算法实现 1. 简化版SMO算法 2. 完整版SMO算法 3. 可视化决策结果 六、核函数 1. 线性不可分——高维可分 2. 核函数 …...

mq的作用
使用mq优点 mq是一种常见的中间件,在项目中经常用到,它具有异步、解耦、削峰填谷的作用。 异步 比如下单流程,A服务—>B服务,总的耗时是A耗时时间B耗时时间,而改为A—>mq---->B后,A发送mq后立刻…...
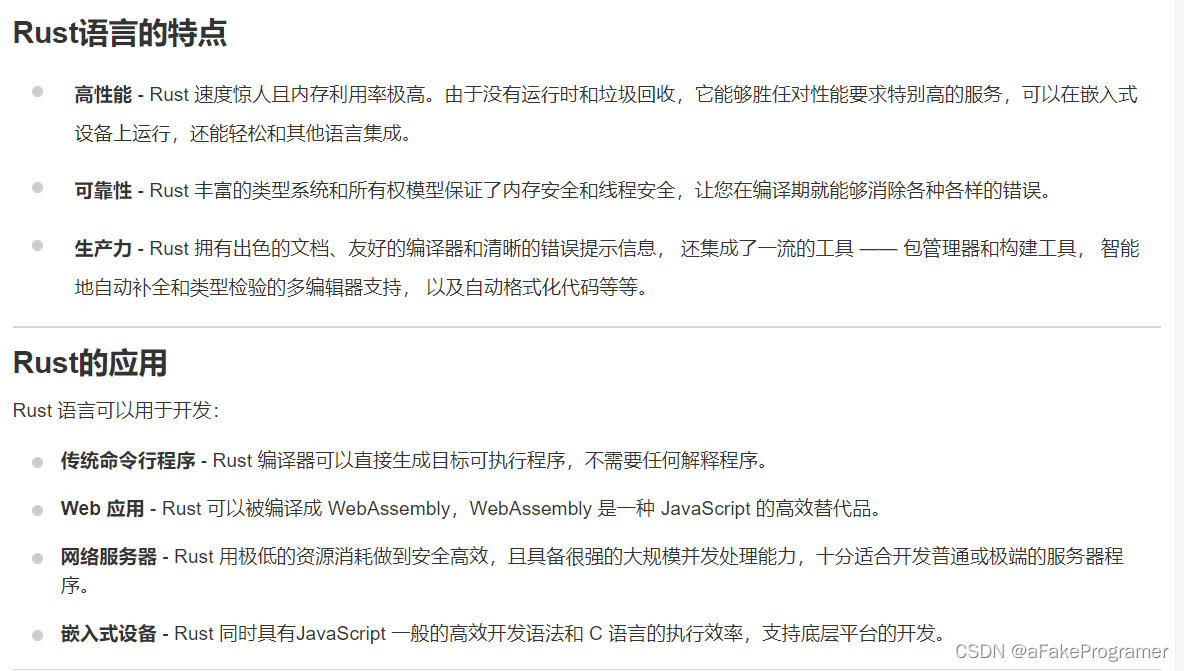
AUTOSAR组织引入了Rust语言的原因是什么?有哪些好处?与C++相比它有什么优点?并推荐一些入门学习Rust语言链接等
AUTOSAR(汽车开放系统架构)是一个由汽车制造商、供应商和其他来自电子、半导体和软件行业的公司组成的全球发展伙伴关系,自2003年以来一直致力于为汽车行业开发和引入开放、标准化的软件平台。 AUTOSAR 最近宣布成立一个新的工作组,用于探索在汽车软件中使用 Rust 编程语言…...
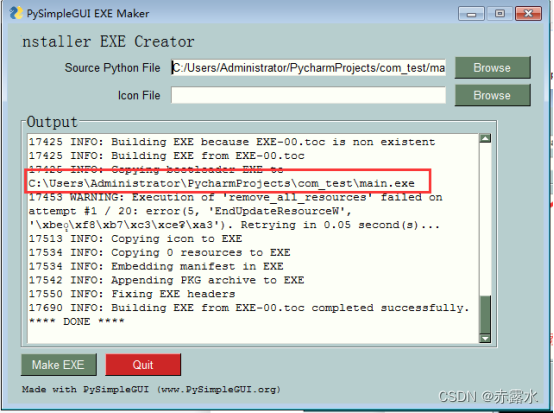
基于PyCharm实现串口GUI编程
工具效果如下如所示 下面简单介绍一下操作流程 1.打开PyCharm软件 2.创建一个工程 3.给该工程命名 4.在main.py里面黏贴如下的代码 # This is a sample Python script. # Press ShiftF10 to execute it or replace it with your code. # Press Double Shift to search everyw…...
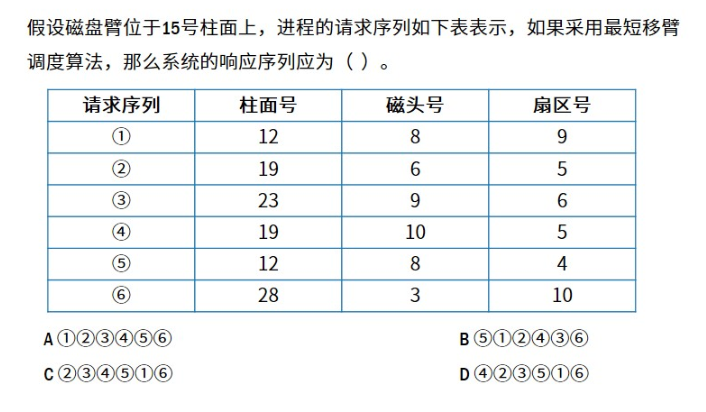
【1.8计算机组成与体系结构】磁盘管理
目录 1.磁盘基本结构与存取过程1.1 磁盘基本结构1.2 磁盘的存取过程 2.磁盘优化分布存储3.磁盘单缓冲区与双缓冲区4.磁盘移臂调度算法 1.磁盘基本结构与存取过程 1.1 磁盘基本结构 磁盘:柱面,磁道,扇区。 1.2 磁盘的存取过程 存取时间寻…...

1663:【 例 1】取石子游戏 1
【题目描述】 有一种有趣的游戏,玩法如下: 玩家: 2 人; 道具: N 颗石子; 规则: 1、游戏双方轮流取石子; 2、每人每次取走若干颗石子(最少取 1 颗,最多取…...

Django去访问web api接口Object of type Session is not JSON serializable
解决方案:settings.py中加入 :SESSION_SERIALIZER django.contrib.sessions.serializers.PickleSerializer 事由:Django去访问一个web api接口,两次连接之间需要通过Session()保持身份验证。 def sendCode(request): mobile jso…...
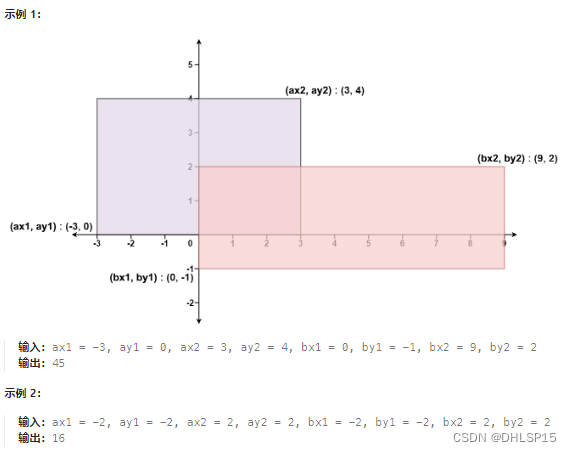
每日一题,二维平面
给你 二维 平面上两个 由直线构成且边与坐标轴平行/垂直 的矩形,请你计算并返回两个矩形覆盖的总面积。 每个矩形由其 左下 顶点和 右上 顶点坐标表示: 第一个矩形由其左下顶点 (ax1, ay1) 和右上顶点 (ax2, ay2) 定义。 第二个矩形由其左下顶点 (bx1, …...

【jupyter notebook】jupyter notebook 调用另一个jupyter notebook 的函数
总结 使用 %run 魔法命令将 Notebook 转换为py文件使用 nbimporter 库手动复制代码优点notebook最前面加上即可最基本方法就跟导入py文件一样,不会被执行一遍快缺点所有的代码都会执行一遍修改原文件就要重新转换,且 从自定义的 .py 文件中导入函数时&a…...

Linux--学习记录(3)
G重要编译参数 -g(GDB调试) -g选项告诉gcc产生能被GNU调试器GDB使用的调试信息,以调试程序编译带调试信息的可执行文件g -g hello.c -o hello编译过程: -E(预处理) g -E hello.c -o hello.i-S(编…...
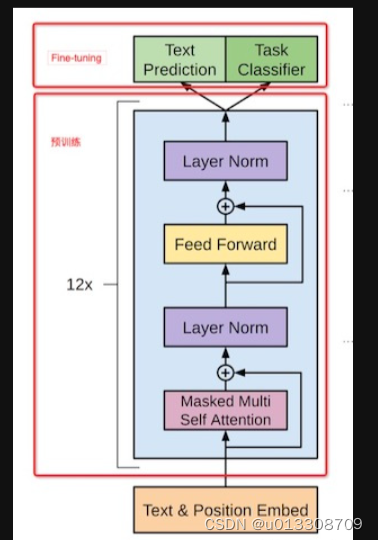
自然语言处理阅读第一弹
Transformer架构 encoder和decoder区别 Embeddings from Language Model (ELMO) 一种基于上下文的预训练模型,用于生成具有语境的词向量。原理讲解ELMO中的几个问题 Bidirectional Encoder Representations from Transformers (BERT) BERT就是原生transformer中的Encoder两…...

Spring Boot+Mybatis设置sql日志打印
在全局配置文件添加以下内容:logging.level.com.demo.mapperdebug,com.demo.mapper:src下的mapper路径,debug:设置日志打印级别为debug,亦可设置为:ERROR、WARN、INFO application.properties …...

步进电机电流设置的3种方法
本文介绍步进电机电流设置的3种方法。 步进电机电流设置包括运行电流(IRun)和保持电流(IHold)2种。电机运行时需要有较大电流以保证有足够的力矩使物体运动,而停止的时候,为了减少电机发热及降低功耗&…...

uniapp-使用返回的base64转换成图片
在实际开发的时候 需要后端实时的给我返回二维码 他给我返回的是加密后的base64字符串 我需要利用这个base64转换到canvas画布上展示 或者以图片的形式展示在页面内 在canvas画布上展示 使用官方的uni.getFileSystemManager().writeFile()方法可将base64码转成的二维码显示在…...

有机面条市场分析:到2026 年的复合年增长率为 5.4%
近年来,有机面条因其健康益处和可持续性而广受欢迎。由于消费者对健康和天然食品的需求不断增加,预计 全球有机面条市场将继续以显着速度增长。特别是中国市场,由于健康意识的提高以及对有机和天然产品的兴趣 增加,有机面条消费量…...

广州设计周落幕|值得被歌颂的奥力斯特岩板
12月11日,一年一度的广州设计周,为期四天的展会在广州保利世贸博览馆、广州国际采购中心和南丰国际会展中心三大展馆已落下帷幕。依旧熙攘,依旧热烈,远道而来的专家领导、媒体嘉宾、展商代表、外国友人、设计爱好者,风…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...
