C++ 二叉搜索树(BST)的实现(非递归版本与递归版本)与应用
C++ 二叉搜索树的实现与应用
- 一.二叉搜索树的特点
- 二.我们要实现的大致框架
- 三.Insert
- 四.InOrder和Find
- 1.InOrder
- 2.Find
- 五.Erase
- 六.Find,Insert,Erase的递归版本
- 1.FindR
- 2.InsertR
- 3.EraseR
- 七.析构,拷贝构造,赋值运算符重载
- 1.析构
- 2.拷贝构造
- 3.赋值运算重载
- 八.Key模型完整代码
- 九.二叉搜索树的应用
- 1.Key模型
- 2.Key-Value模型
二叉搜索树既可以实现为升序版本,也可以实现为降序版本
本文实现为升序版本
一.二叉搜索树的特点
二叉搜索树是一种特殊的二叉树
它的特点是:
1.左子树的所有节点均比根节点的值小
2.右子树的所有节点均比根节点的值大
3.左右子树都是二叉搜索树
4.中序遍历序列是有序的
5.一般二叉搜索树不允许有重复值
当然,二叉搜索树默认是升序的,不过也可以实现成降序的样子
只需要更改一下第1条和第2条即可,
第一条改为左子树的节点都要大于根节点
第二条改为右子树的节点都要小于根节点
此时实现出来的二叉搜索树就是降序的
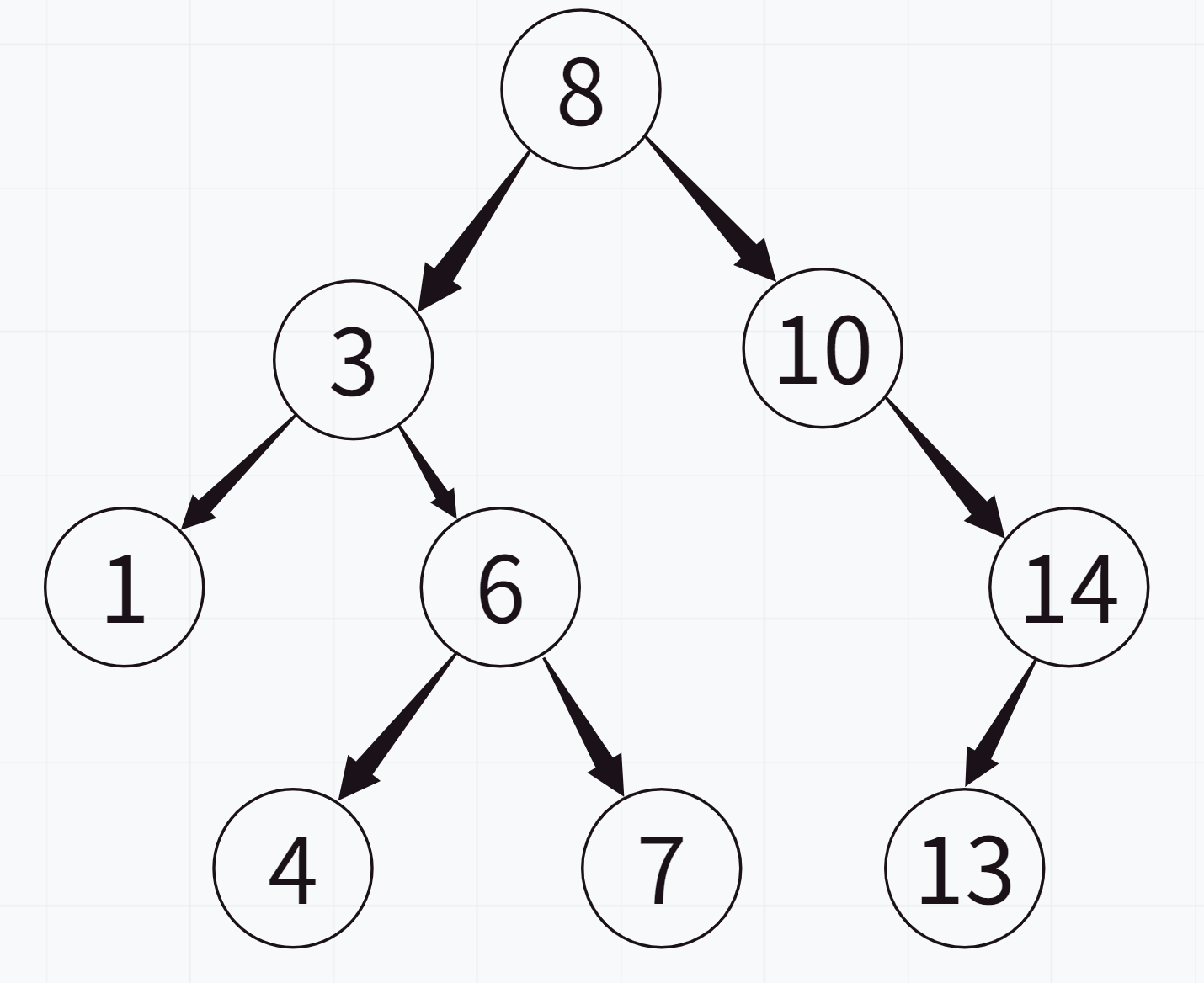
例如:这个树就是一个二叉搜索树
二.我们要实现的大致框架
#pragma once
#include <iostream>
using namespace std;
//BST排升序:左孩子小于我, 右孩子大于我
//排降序: 左孩子大于我, 右孩子小于我//节点的结构体
template <class K>
struct BSTreeNode
{BSTreeNode<K>* _left = nullptr;BSTreeNode<K>* _right = nullptr;K _key;BSTreeNode(const K& key):_key(key){}
};template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public://非递归实现insert.find,erasebool Insert(const K& key);Node* Find(const K& key);bool Erase(const K& key);//析构函数 后续遍历析构~BSTree();//C++11新语法BSTree() = default;//强制生成默认构造//拷贝构造//先序遍历构造BSTree(const BSTree<K>& bst);//赋值运算符重载:现代版本BSTree<K>& operator=(BSTree<K> bst);void InOrder(){_InOrder(_root);}//递归实现insert.find,eraseNode* FindR(const K& key){return _FindR(_root,key);}bool InsertR(const K& key){return _InsertR(_root, key);}bool EraseR(const K& key){return _EraseR(_root, key);}private://拷贝构造函数的子函数Node* _Copy(const Node* root);//析构函数的子函数void _Destroy(Node*& root);//中序遍历的子函数void _InOrder(Node* root);//find的子函数Node* _FindR(Node* root, const K& key);//insert的子函数bool _InsertR(Node*& root, const K& key);//erase的子函数bool _EraseR(Node*& root, const K& key);//给根节点_root缺省值nullptrNode* _root = nullptr;
};
这是Key模型的版本,最后我们要修改一份Key-Value版本
template <class K>
这里模板给K的原因是:贴合K模型而已,所以没有用T
这里的R : recursion(递归的英文)
//给根节点_root缺省值nullptr
Node* _root = nullptr;
这里直接给根节点_root缺省值nullptr了,编译器默认生成的构造函数就会使用这个缺省值
这里补充一点:
//C++11新语法:给default这个关键字增加了一个含义
BSTree() = default;//强制生成默认构造
三.Insert
学习了二叉搜索树的特点之后,我们来看如何插入一个值
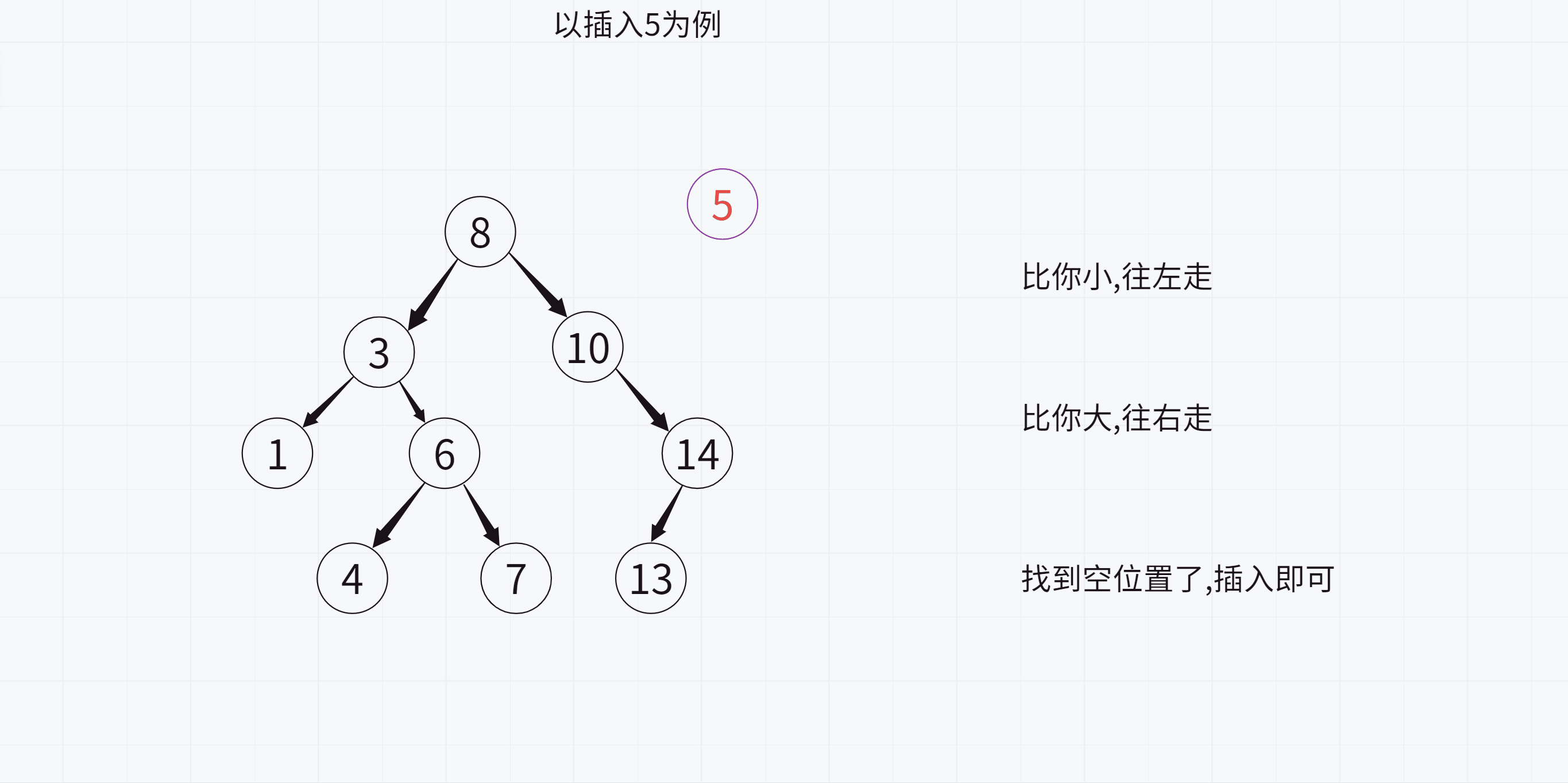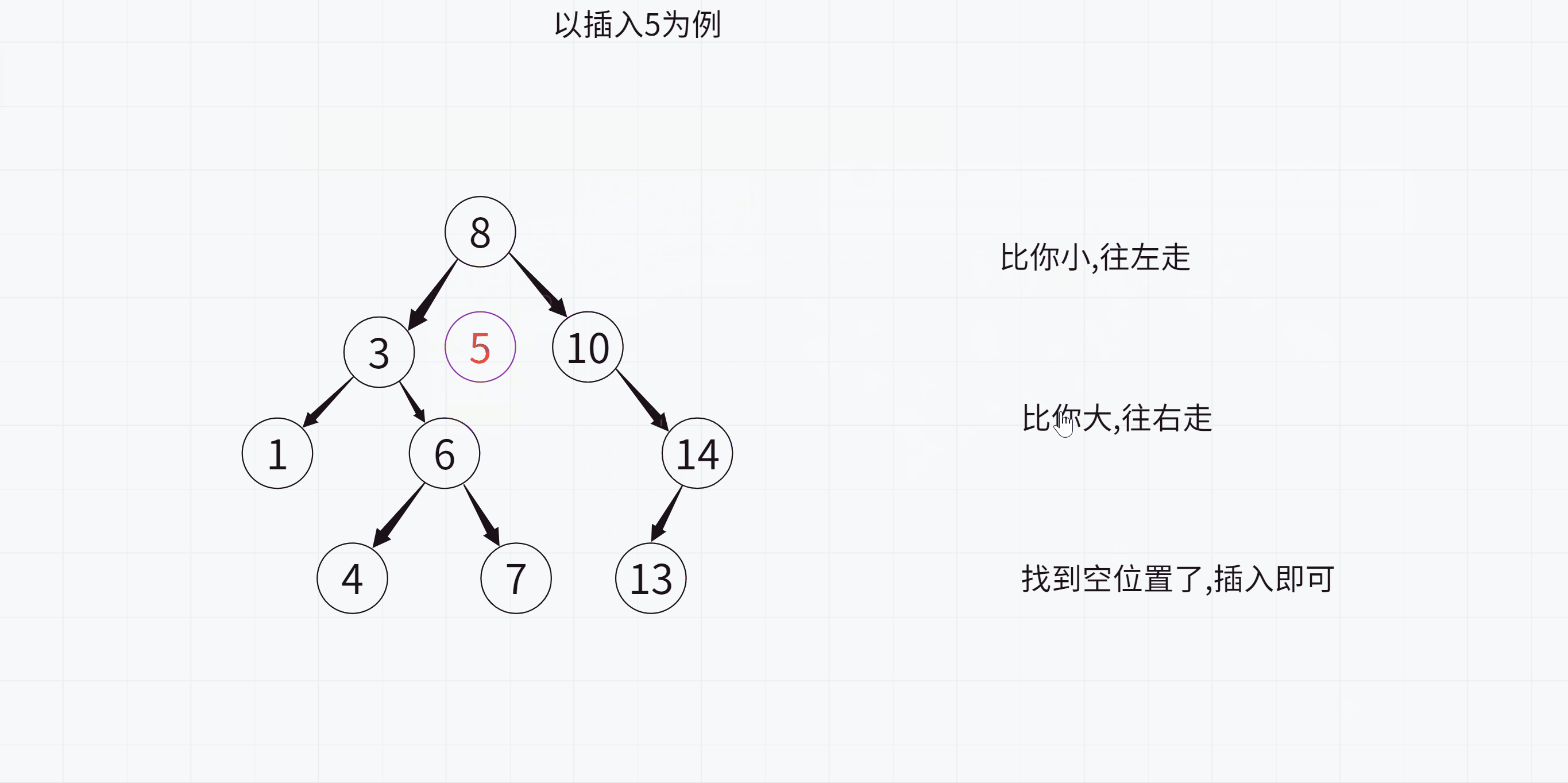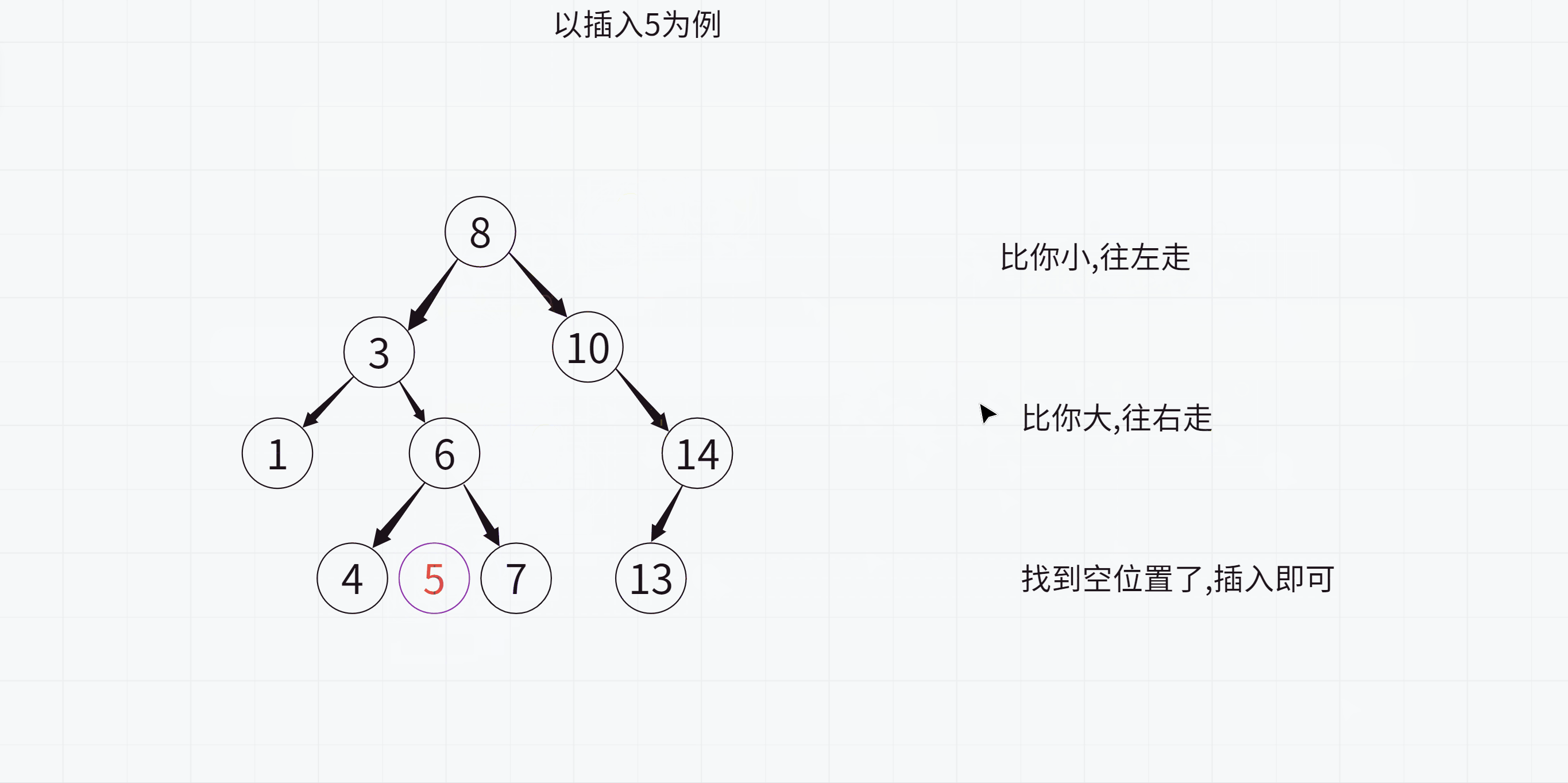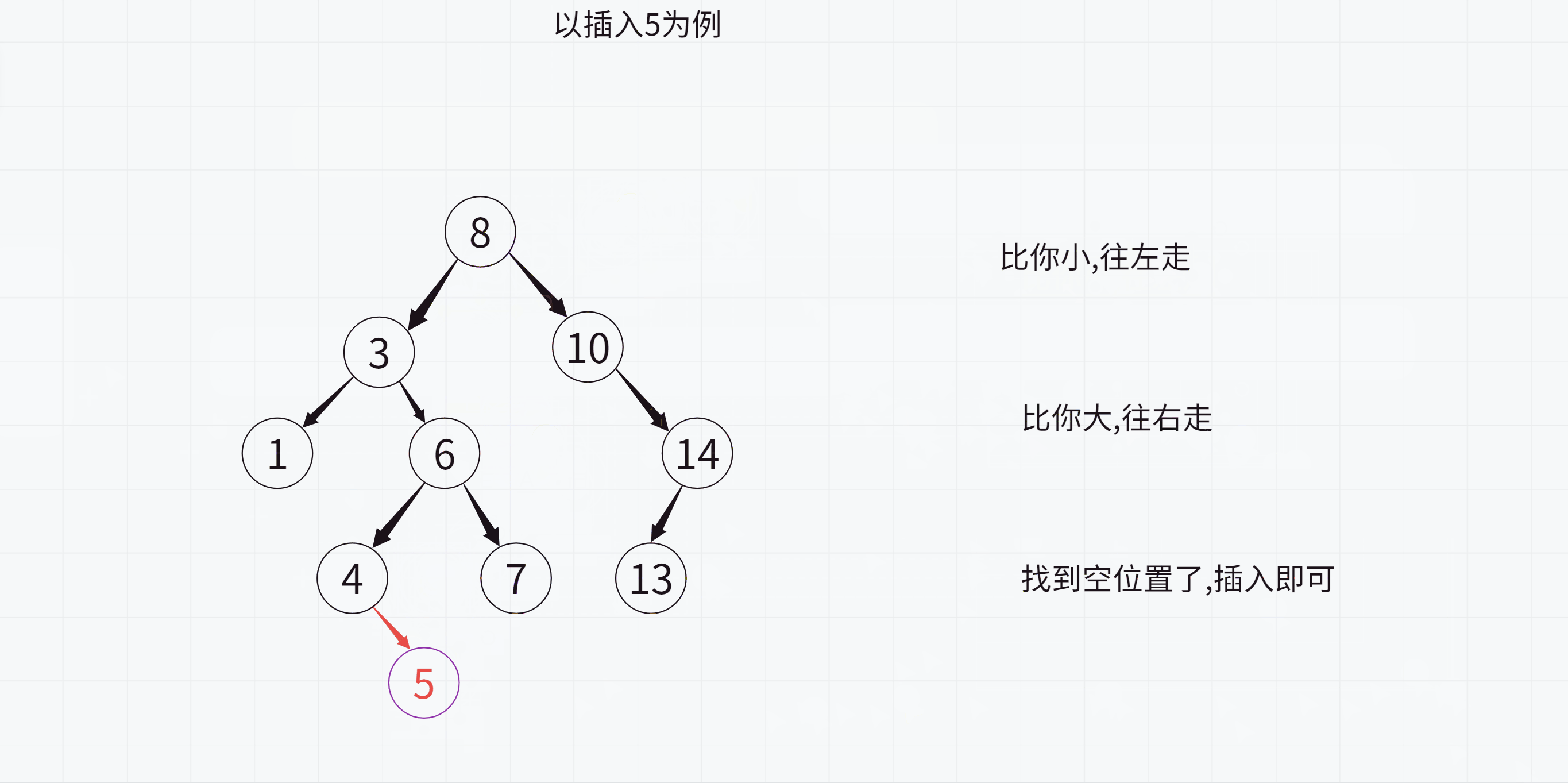
注意:
1.在遍历查找要插入的位置时一定要记录父节点,否则无法插入
2.最后插入的时候要判断该值与父节点的大小关系,这样才能知道要插入到左侧还是右侧
因此我们就可以写出这样的代码
插入成功,返回true
插入失败(说明插入了重复值),返回false
bool Insert(const K& key)
{if (_root == nullptr){_root = new Node(key);return true;}Node* cur = _root;Node* parent = _root;//记录父亲,因为要能够插入while (cur){//要插入的值小于父亲,往左找if (cur->_key > key){parent = cur;cur = cur->_left;}//要插入的值大于父亲,往右找else if (cur->_key < key){parent = cur;cur = cur->_right;}//出现了重复元素,BST搜索二叉树不允许出现重复值,因此不允许插入,返回falseelse{return false;}}//此时cur为空,说明找到了空位置 在此位置插入valuecur = new Node(key);//要插入的元素小于父亲,插入到左侧if (parent->_key > key){parent->_left = cur;}//要插入的元素大于父亲,插入到右侧else{parent->_right = cur;}//插入成功return true;
}
四.InOrder和Find
1.InOrder
关于InOrder中序遍历跟普通二叉树的中序遍历是一模一样的
只不过因为要用递归去实现,而且_root是私有变量不能让外界访问到,因此封装了一个子函数,让子函数去递归完成任务,主函数可以被外界调用到,子函数无需提供给外界
同理,后面的Insert,Erase,Find的递归版本都是封装了一个子函数,跟InOrder这方面的思路一样
void InOrder()
{_InOrder(_root);cout << endl;
}
void _InOrder(Node* root)
{if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);
}
2.Find
学习了Insert之后,Find对我们来说就很简单了
要查找一个值key
1.key小于当前节点的值,往左找
2.key大于当前节点的值,往右找
3.key等于当前节点的值,找到了,返回该节点
4.要查找的当前节点为空节点,返回nullptr,代表查找失败
Node* Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else{return cur;}}//此时cur为空说明没有找到return nullptr;
}
此时我们就可以开始玩这个二叉搜索树了
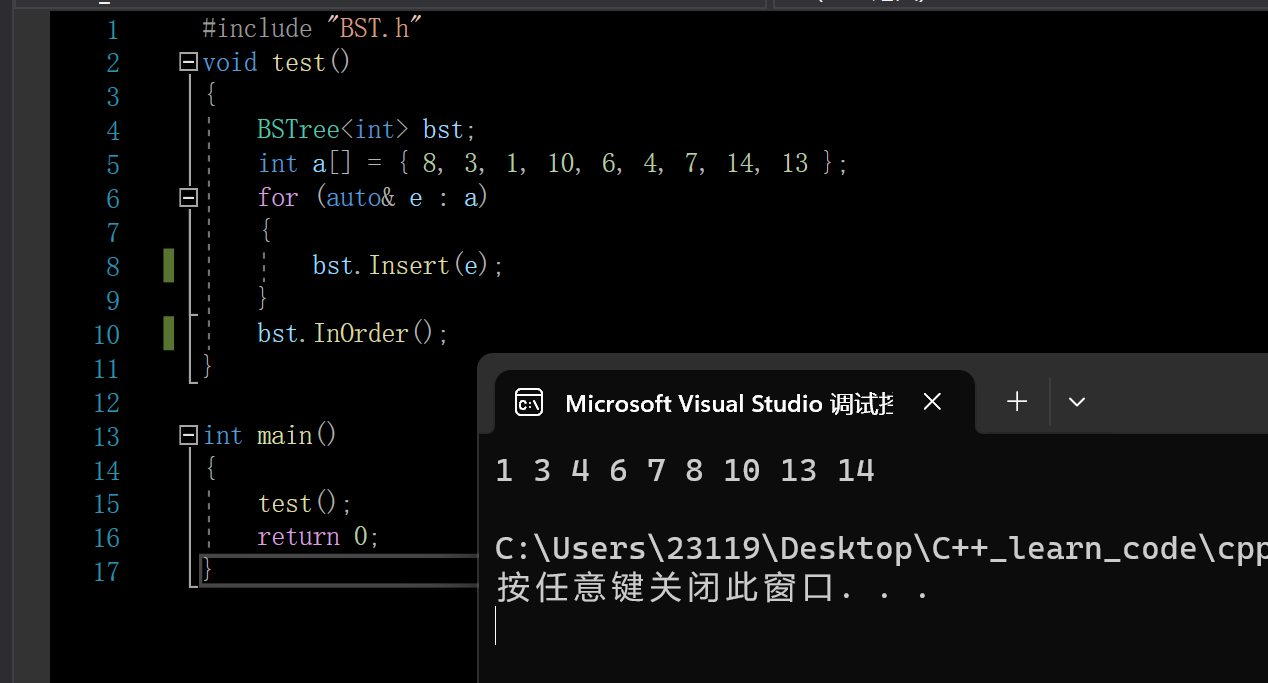
可以看出,中序遍历的确是有序的
五.Erase
前面的insert和find都比较简单,接下来的erase就比较复杂了
erase分为4种情况:
对于要删除的节点
1.该节点没有左孩子,也没有右孩子
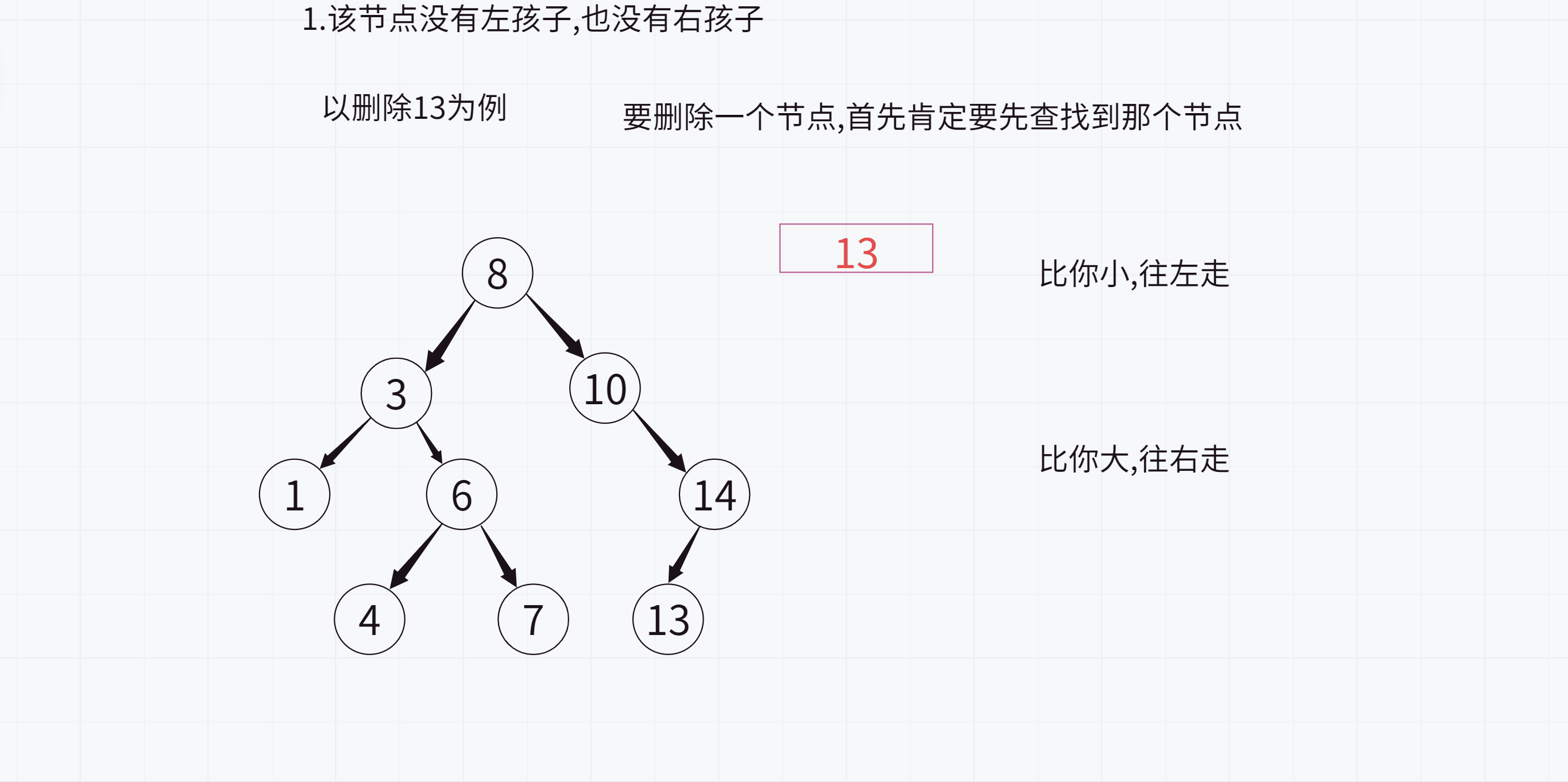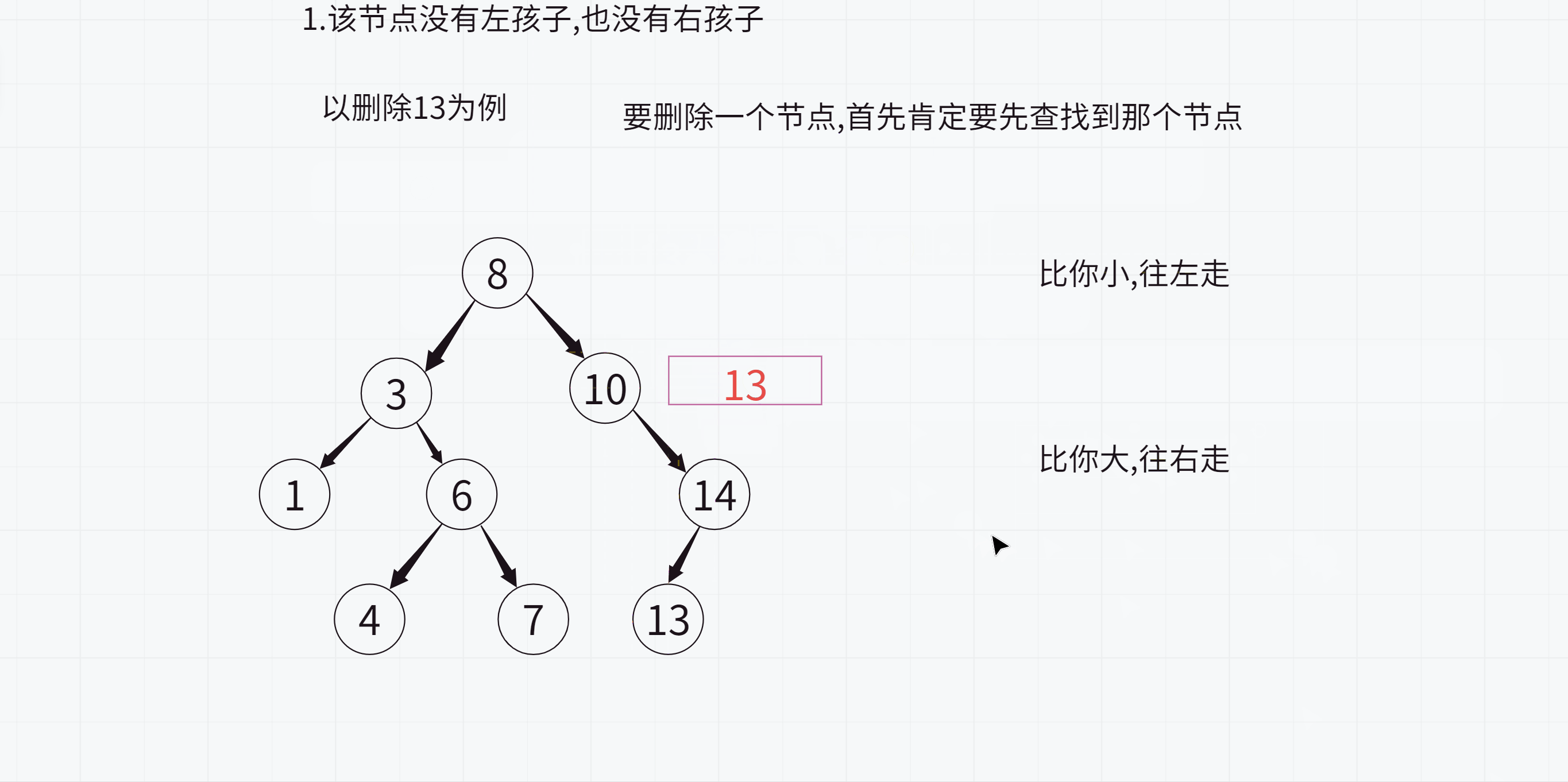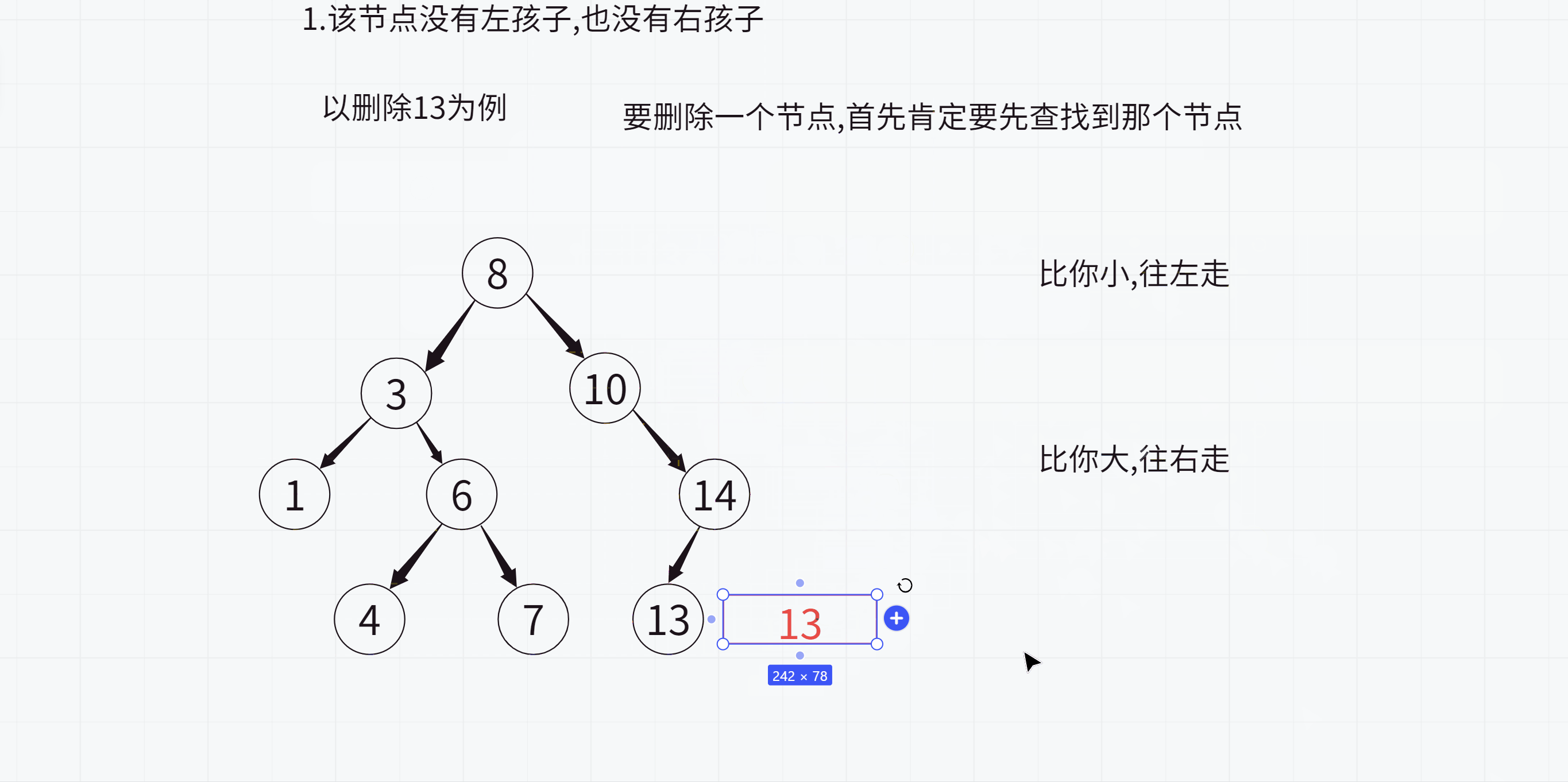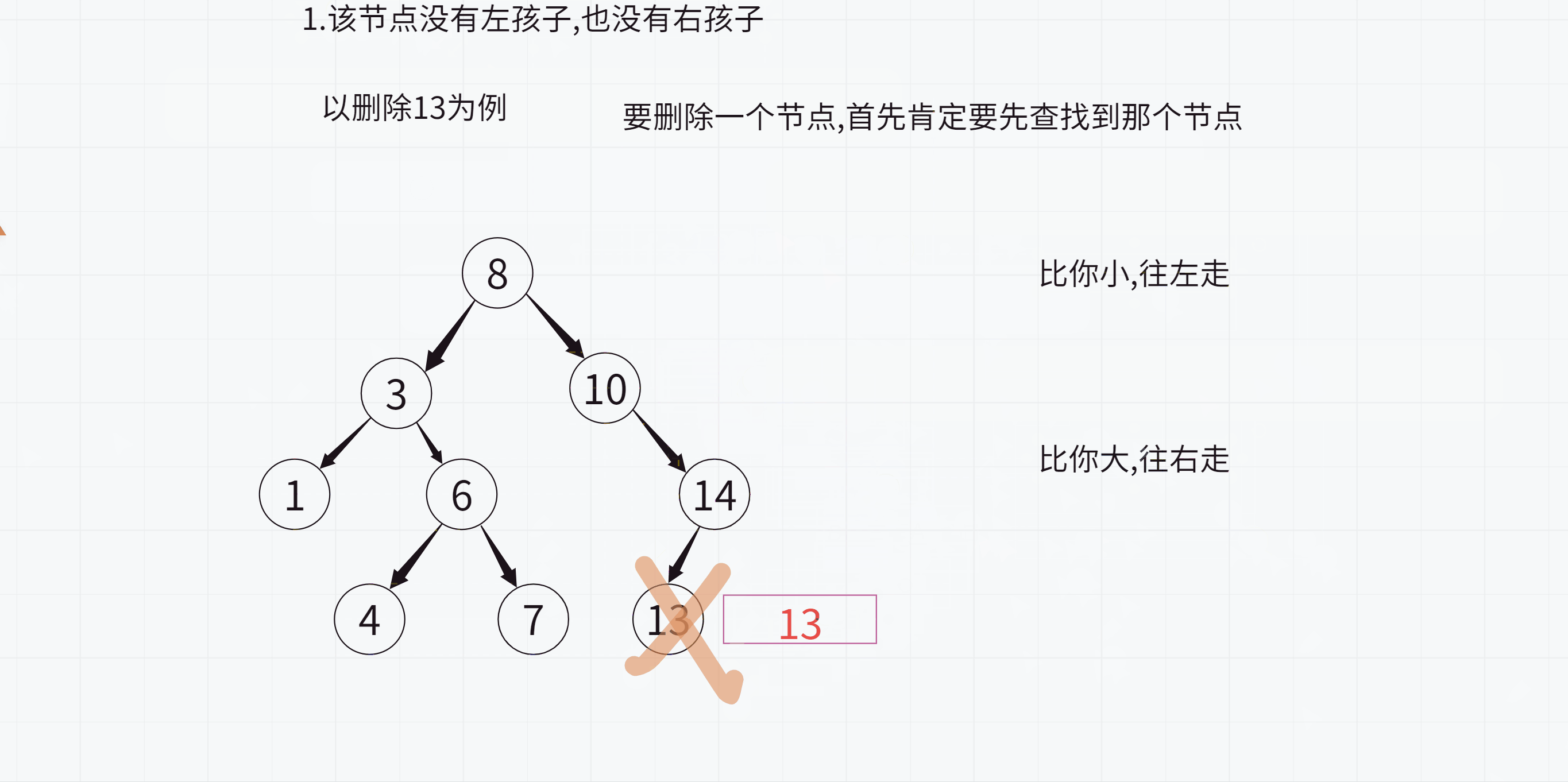
不过这里最后删除的时候是不对的,因为14依旧指向13,而13已经被释放了,所以14的_left指针就成为了野指针,怎么办呢?
此时只需要先让该节点的父亲(也就是14)指向空,
然后就可以放心地删除13了
正确的版本:
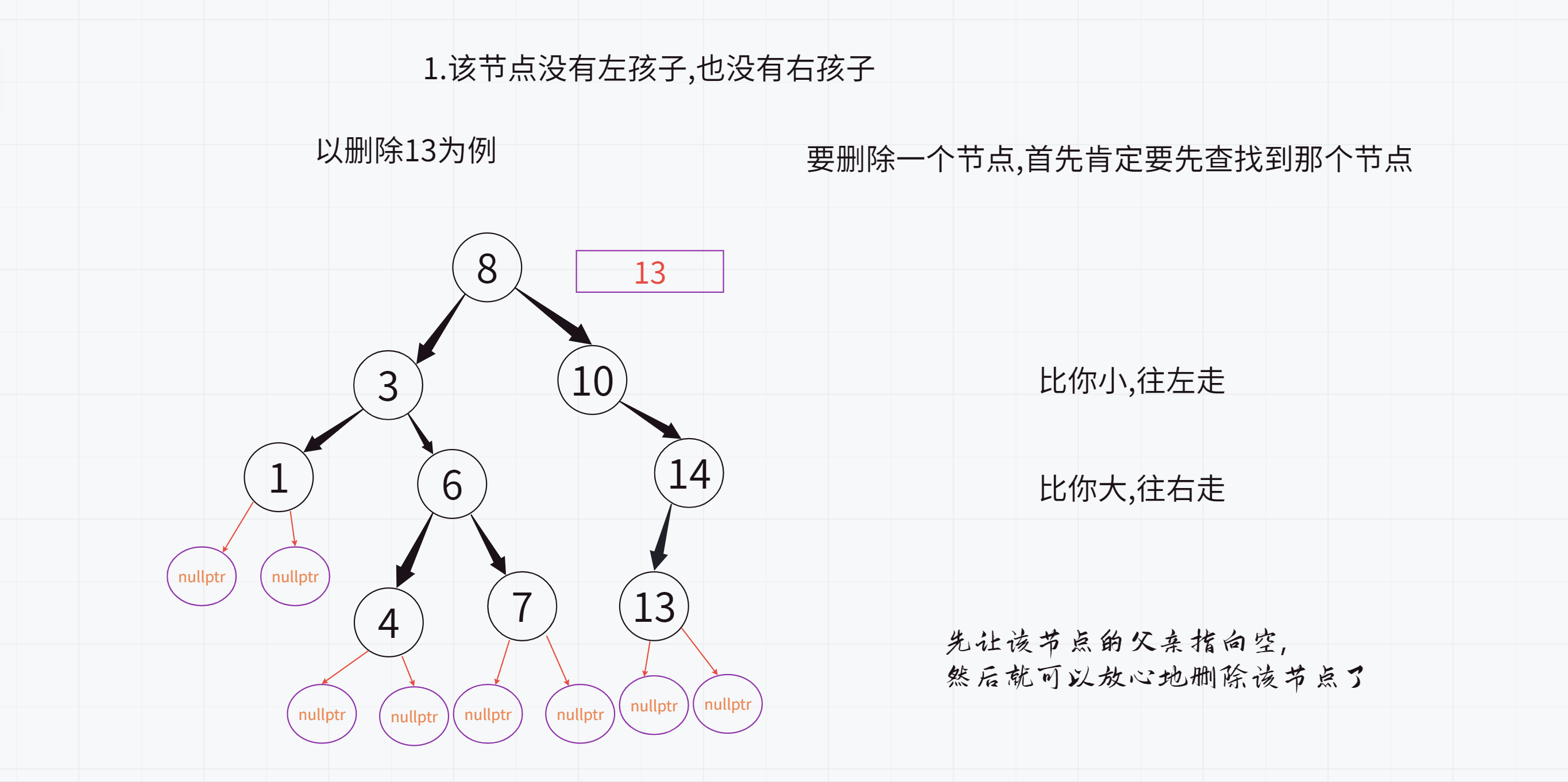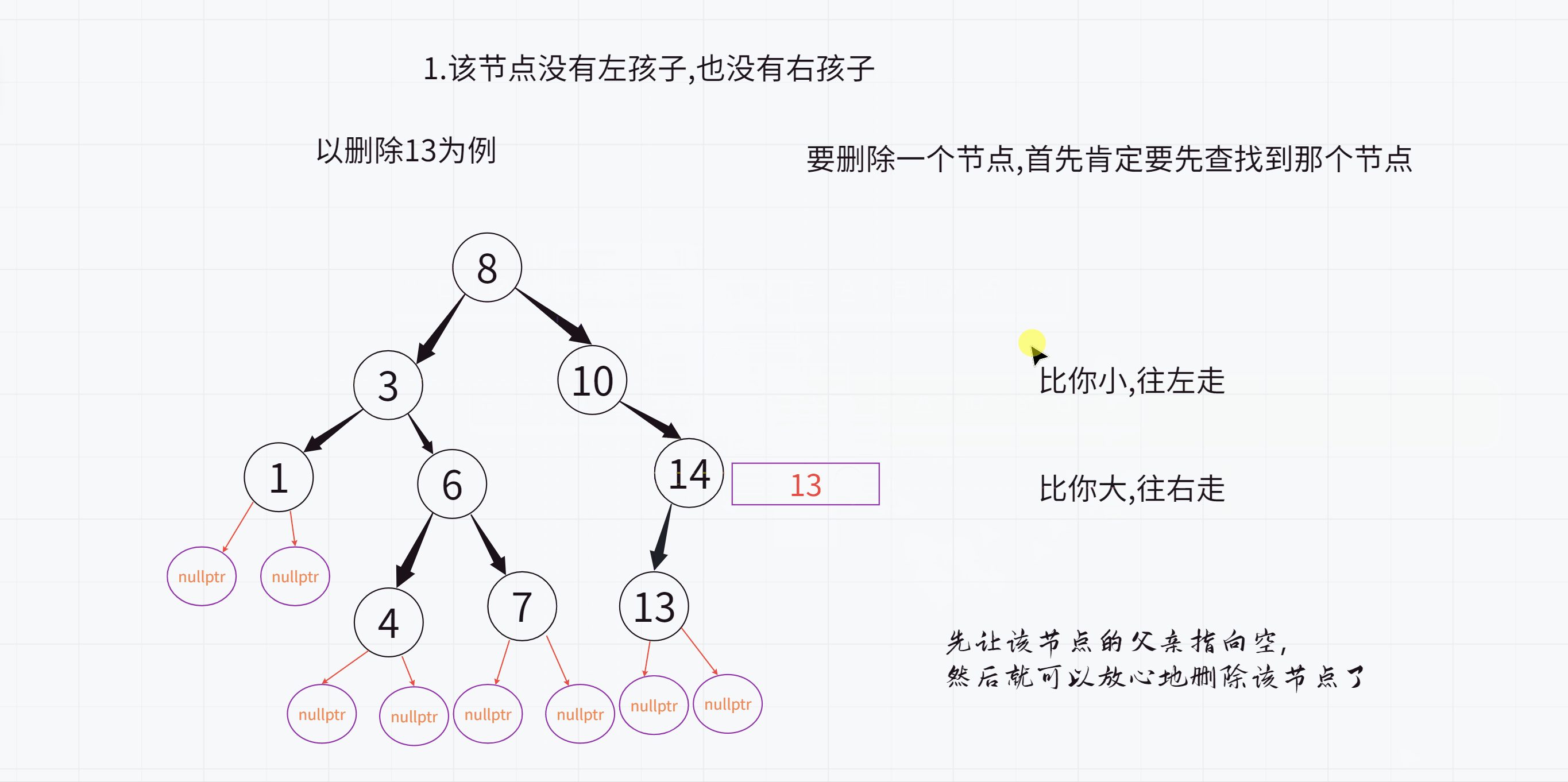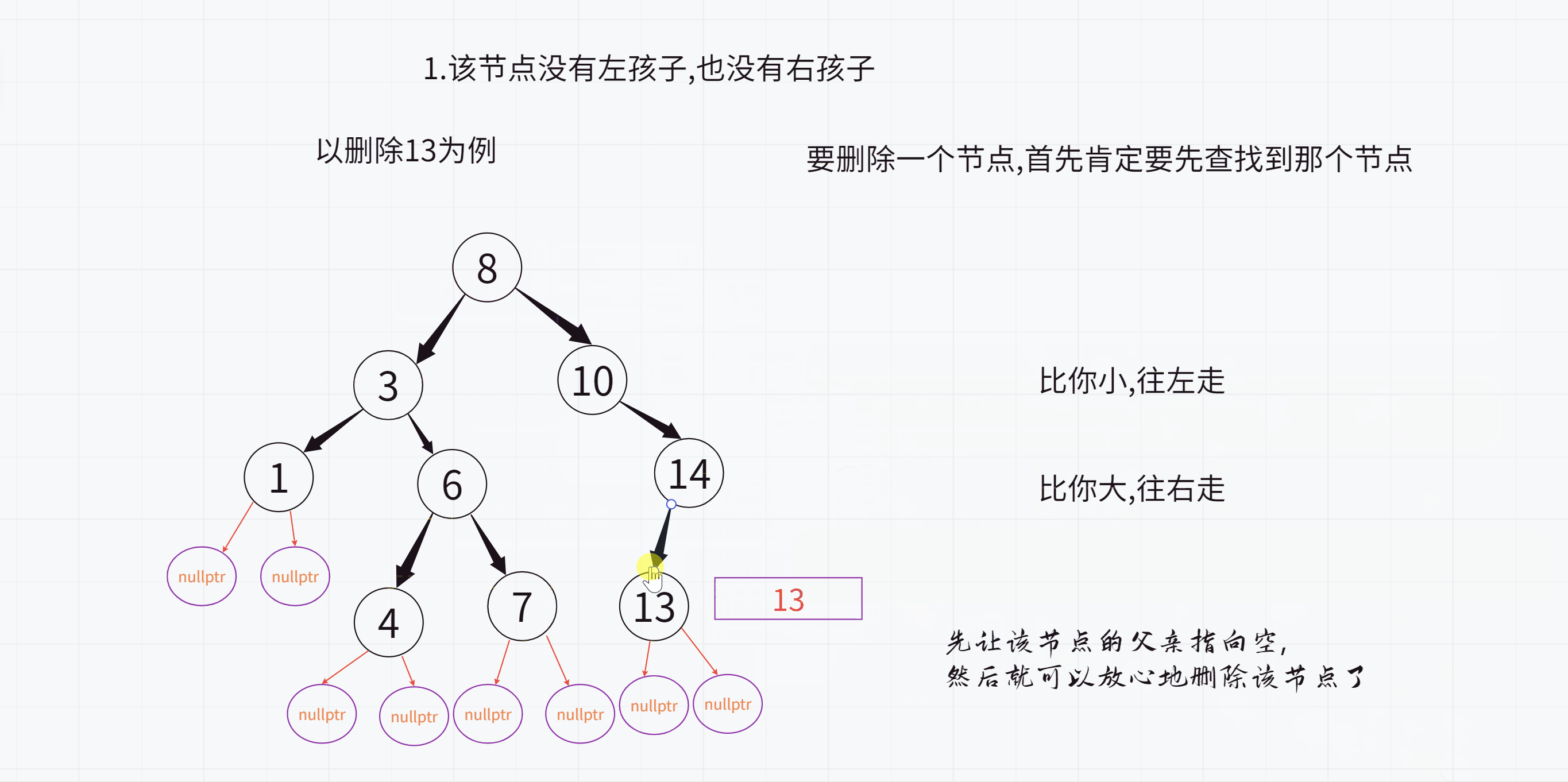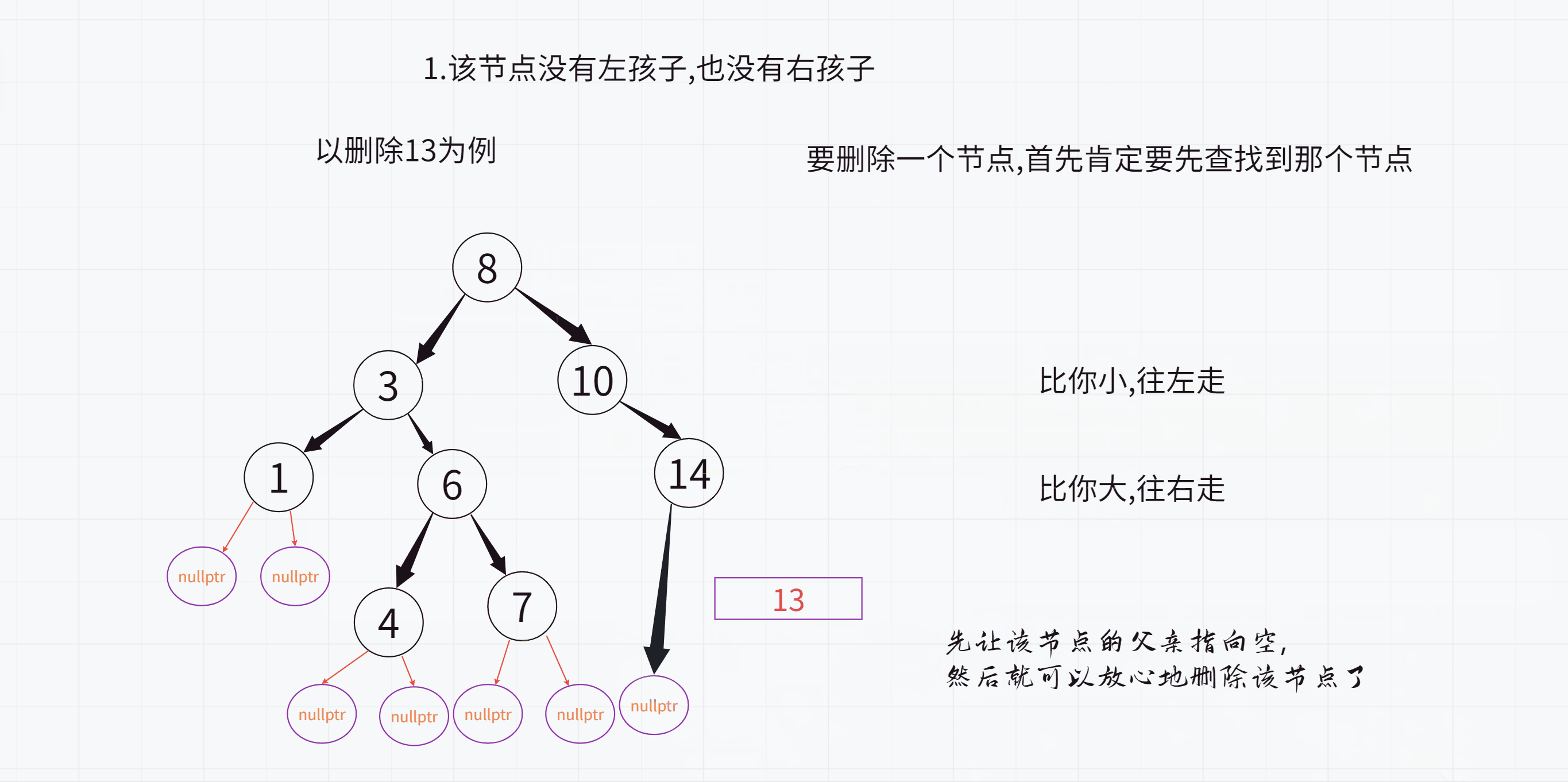
2.该节点没有左孩子,但是有右孩子
此时只需要把该节点的右孩子托付给父亲即可
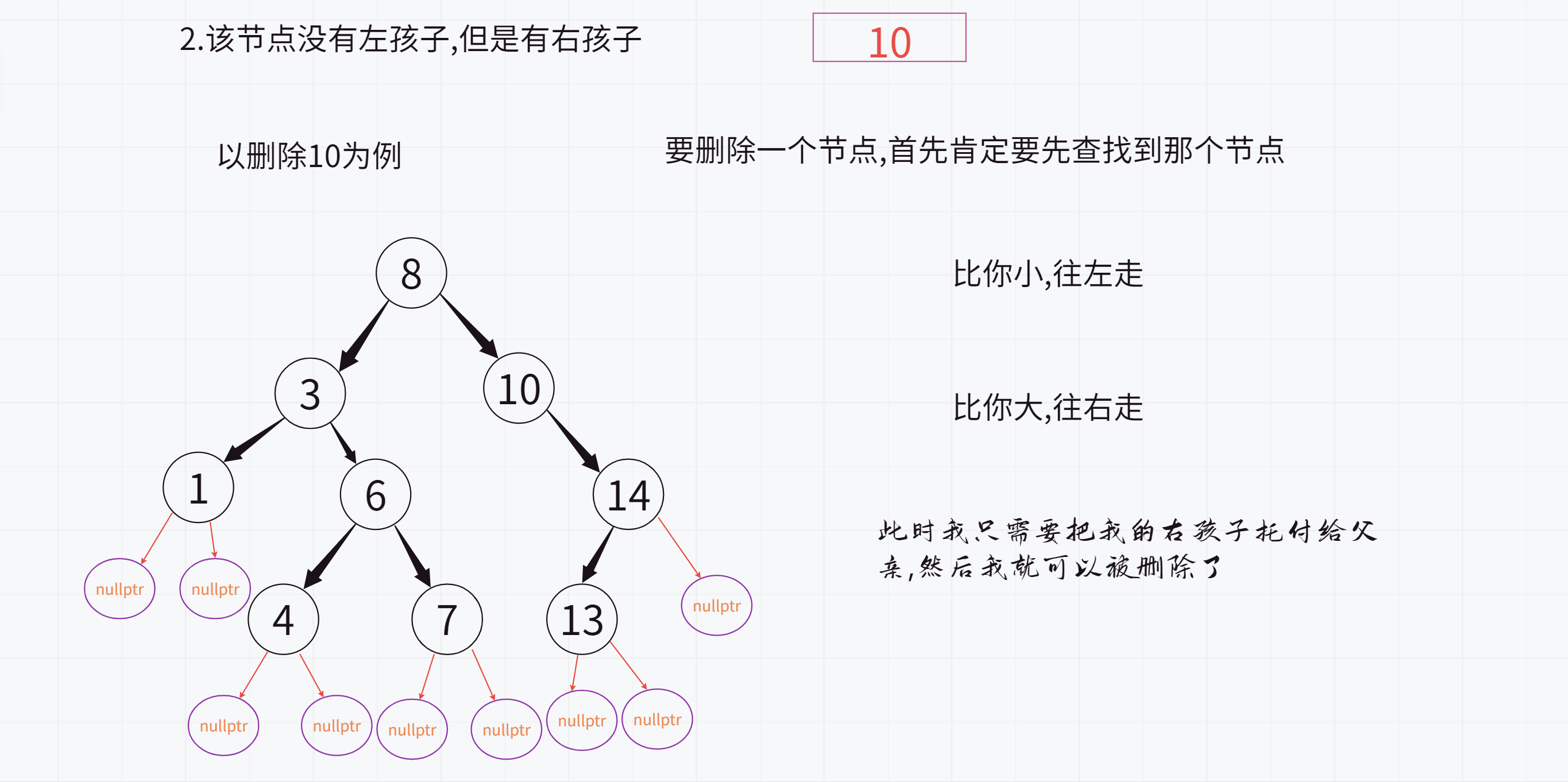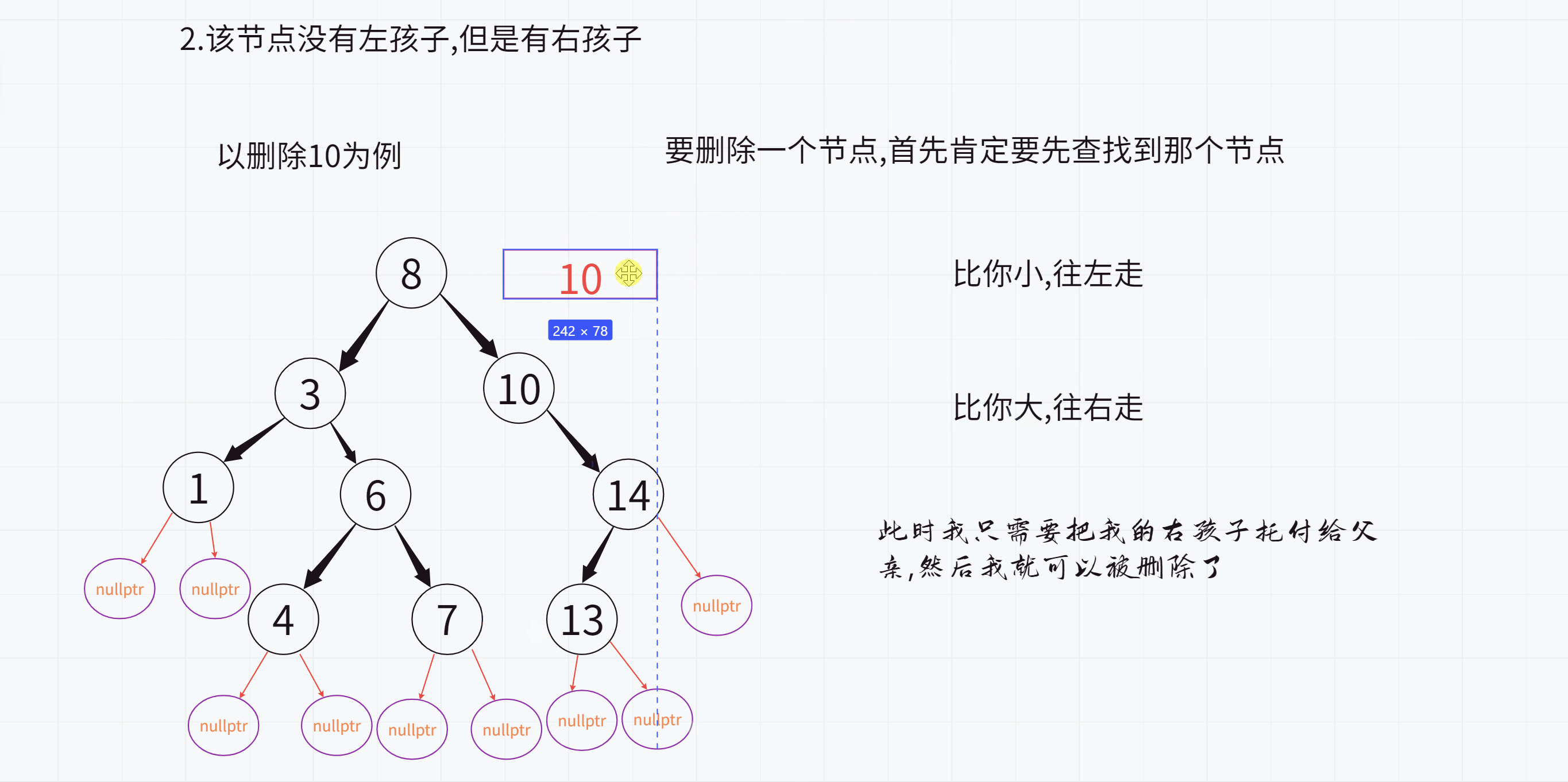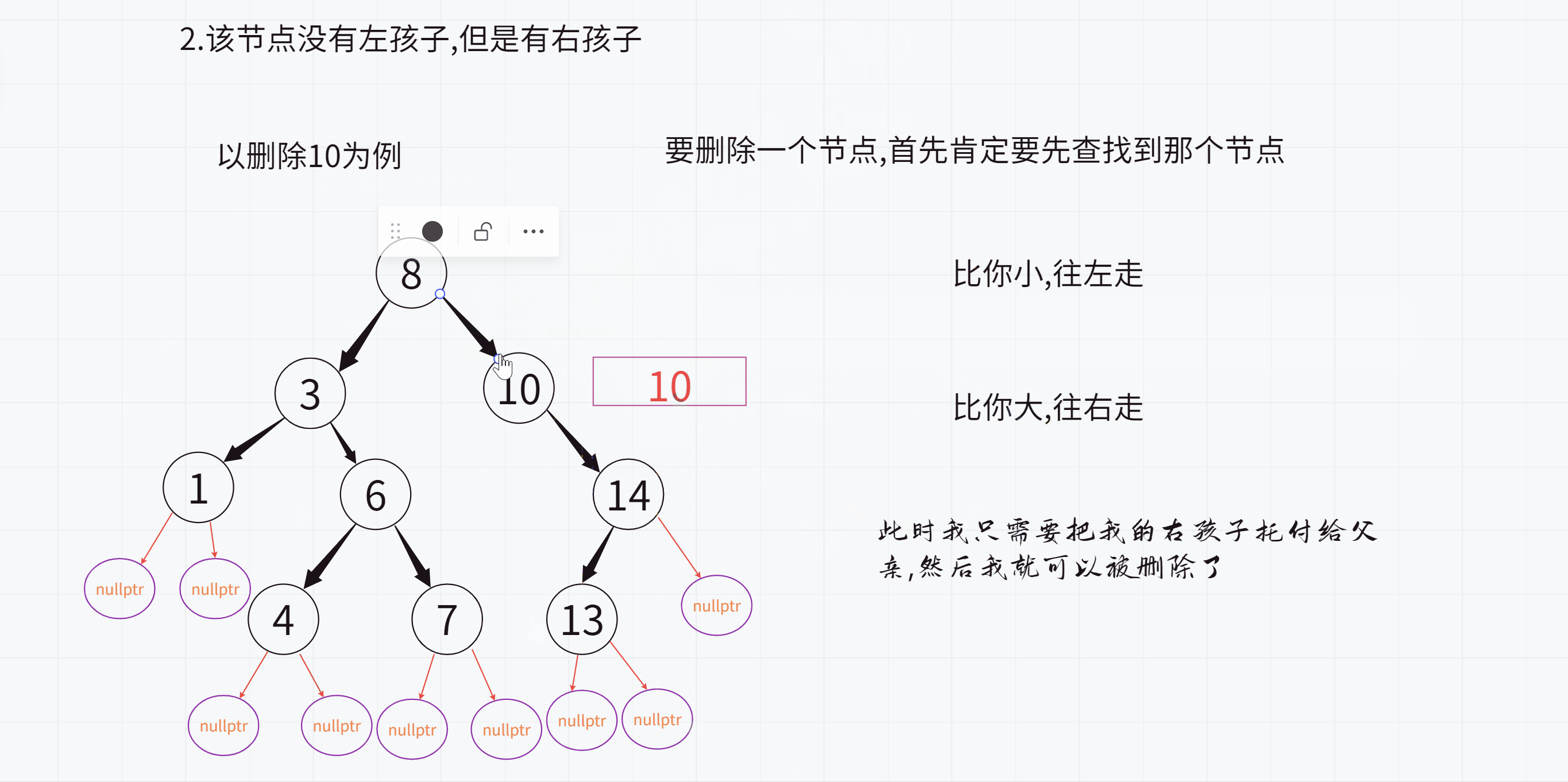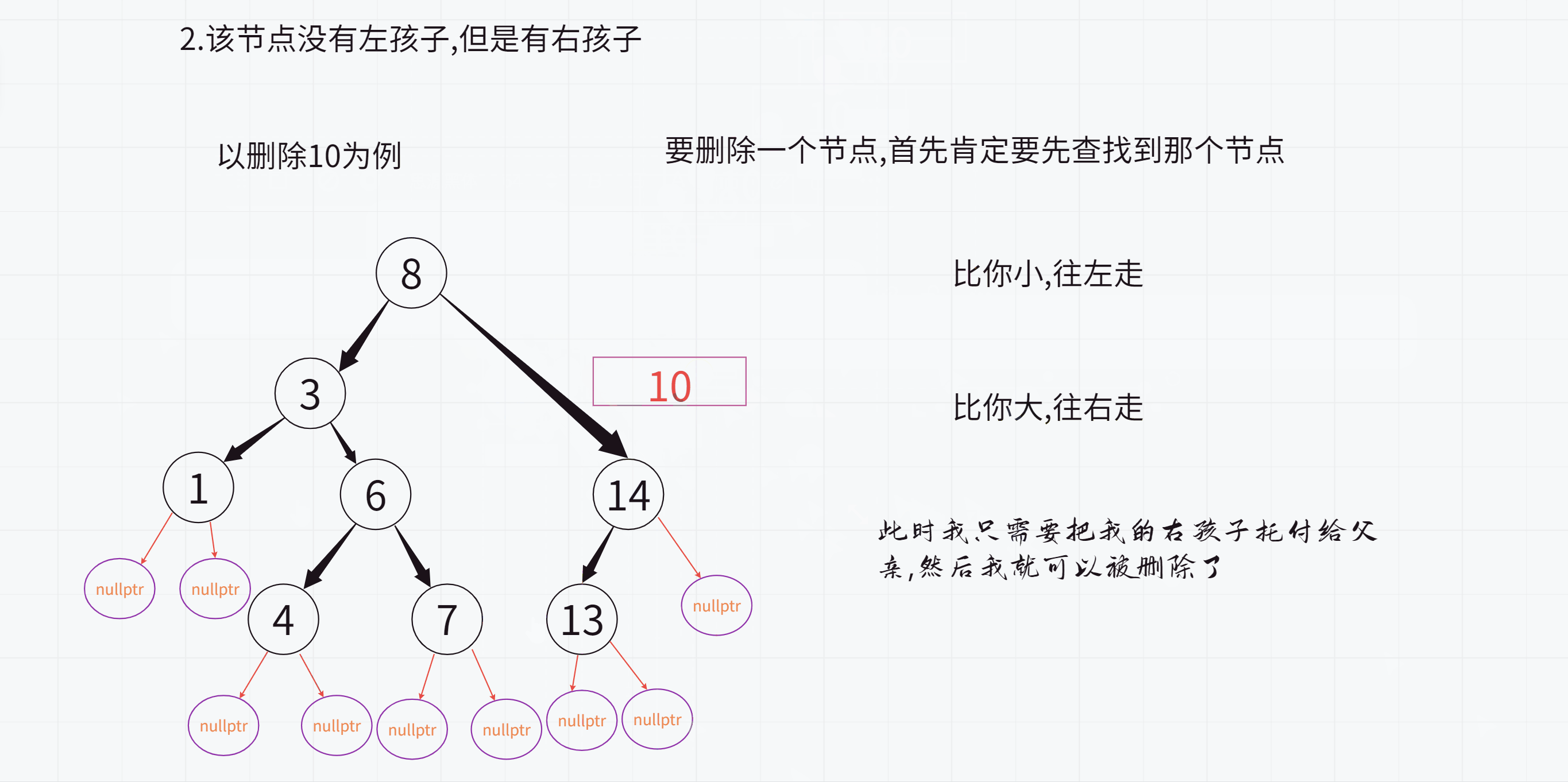
3.该节点有左孩子,不过没有右孩子
此时只需要把该节点的左孩子托付给父亲即可
其实第一类可以归为第二类或者第三类

4.该节点既有左孩子,又有右孩子
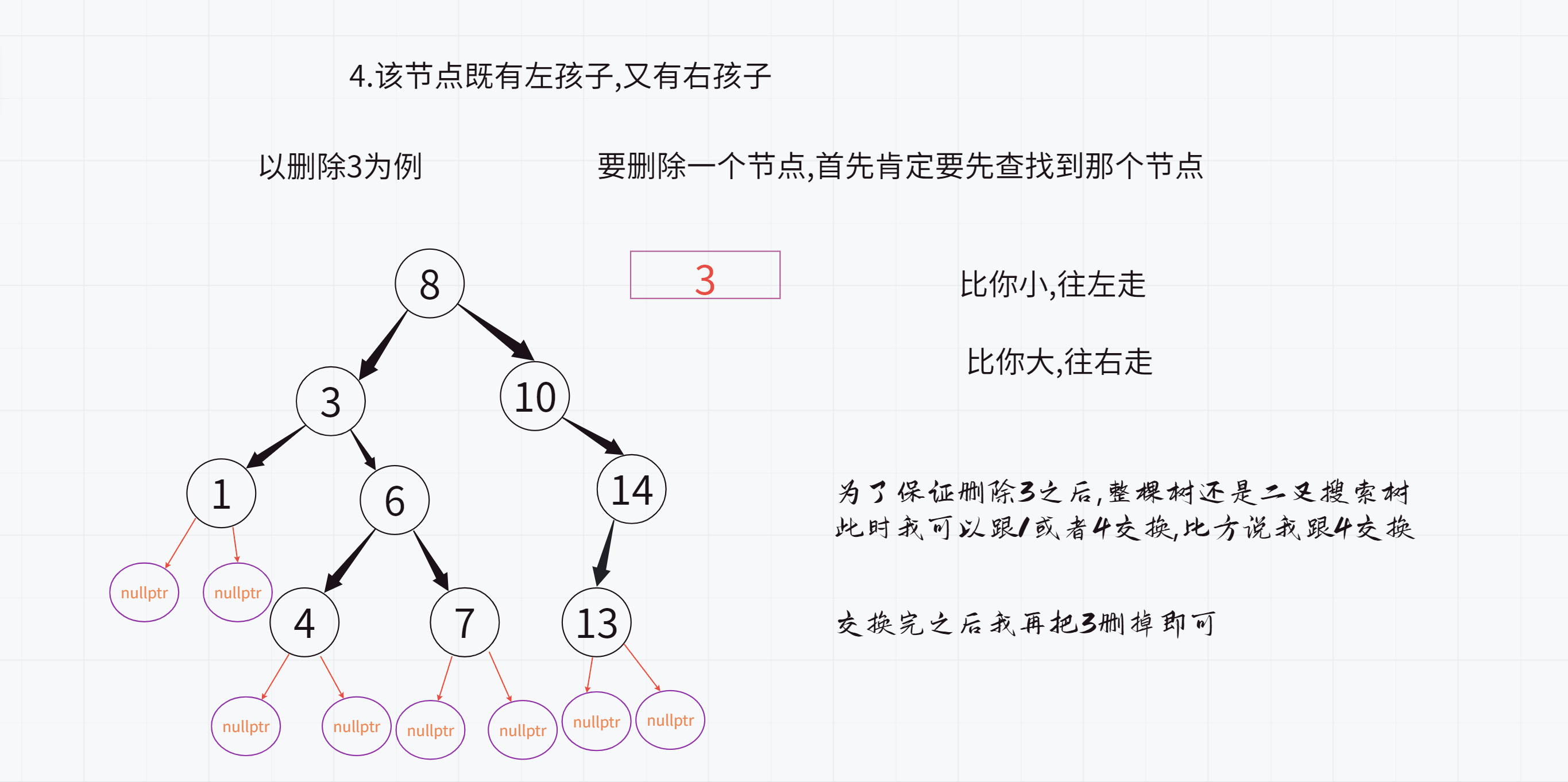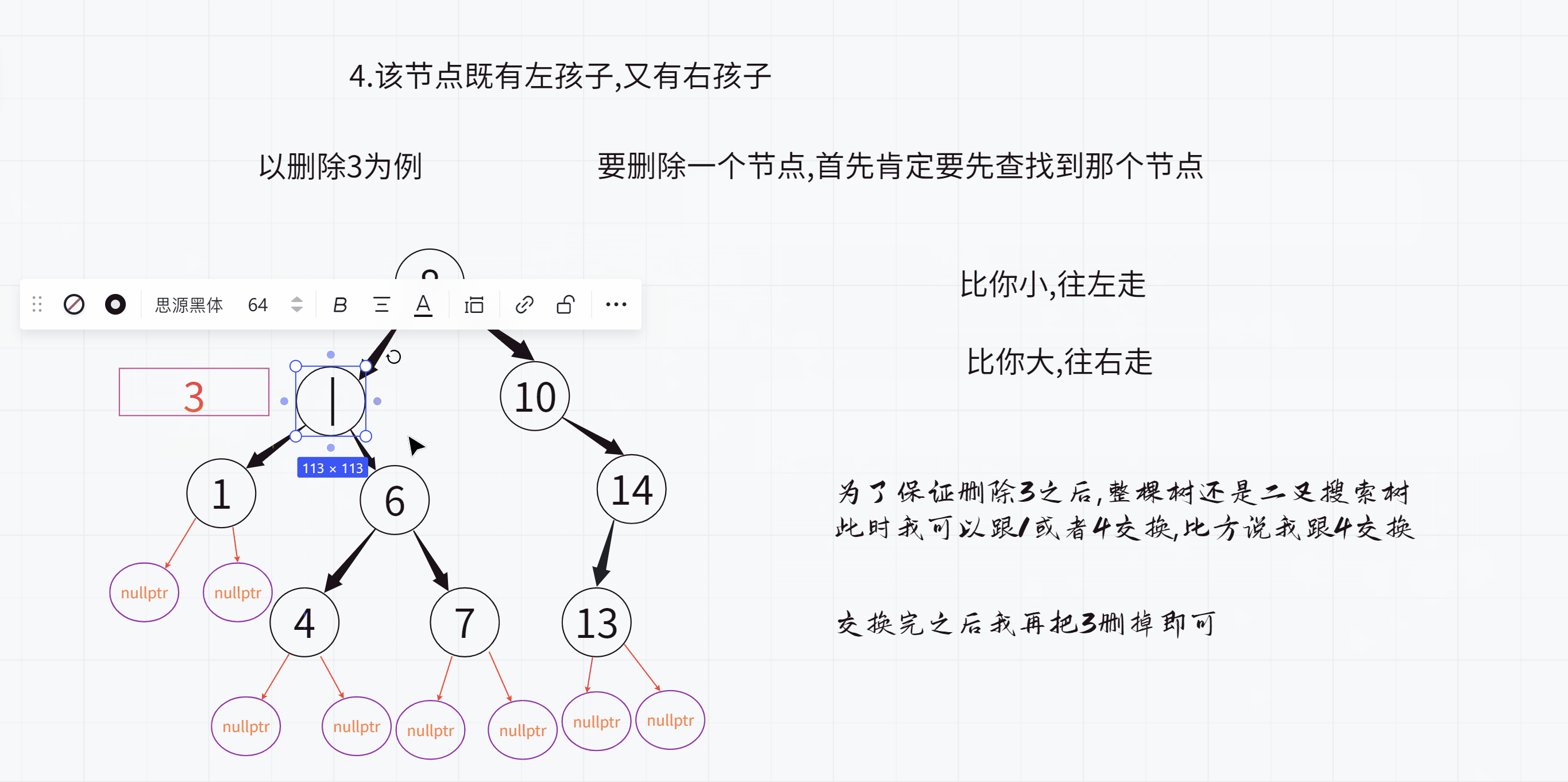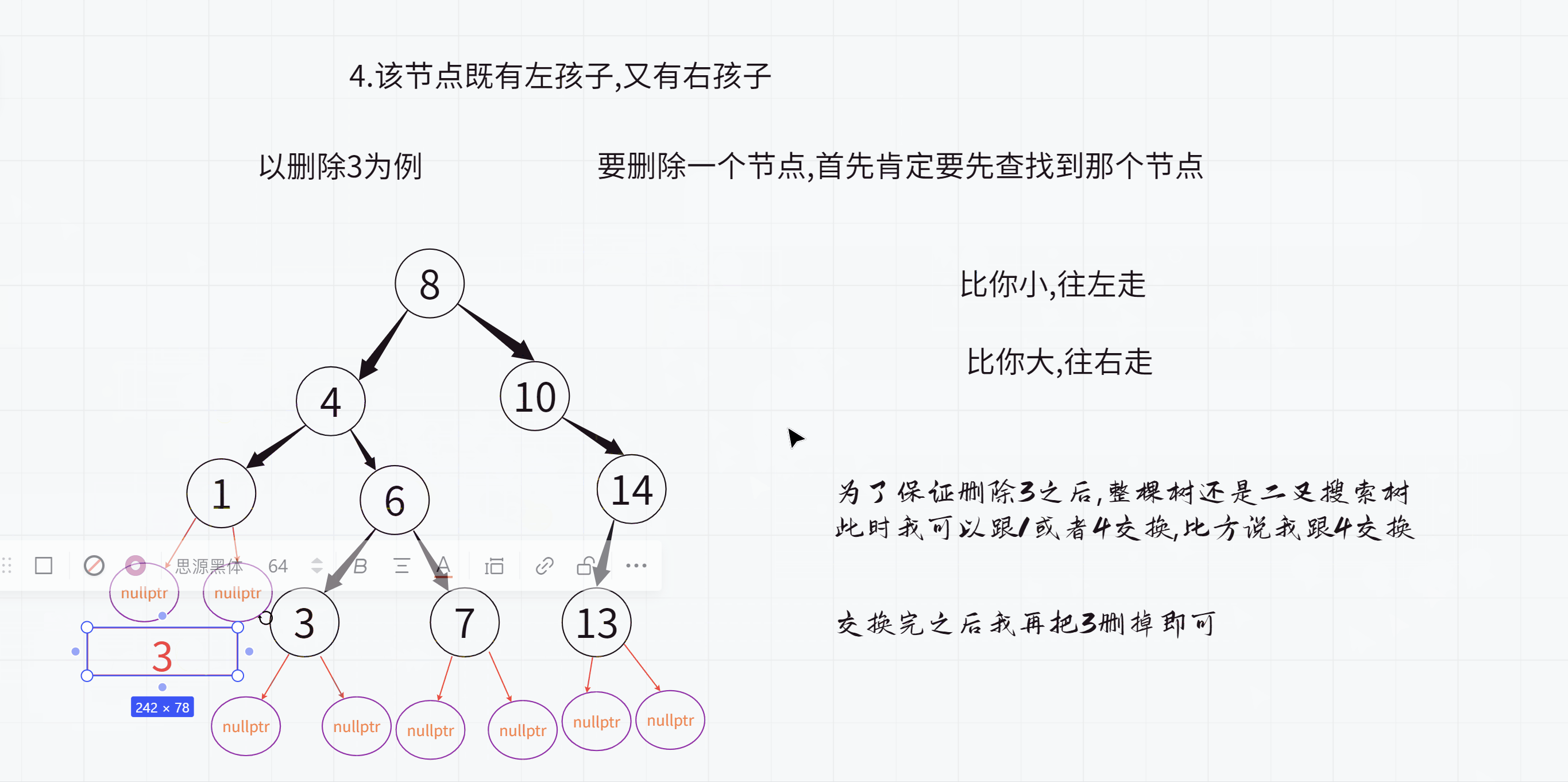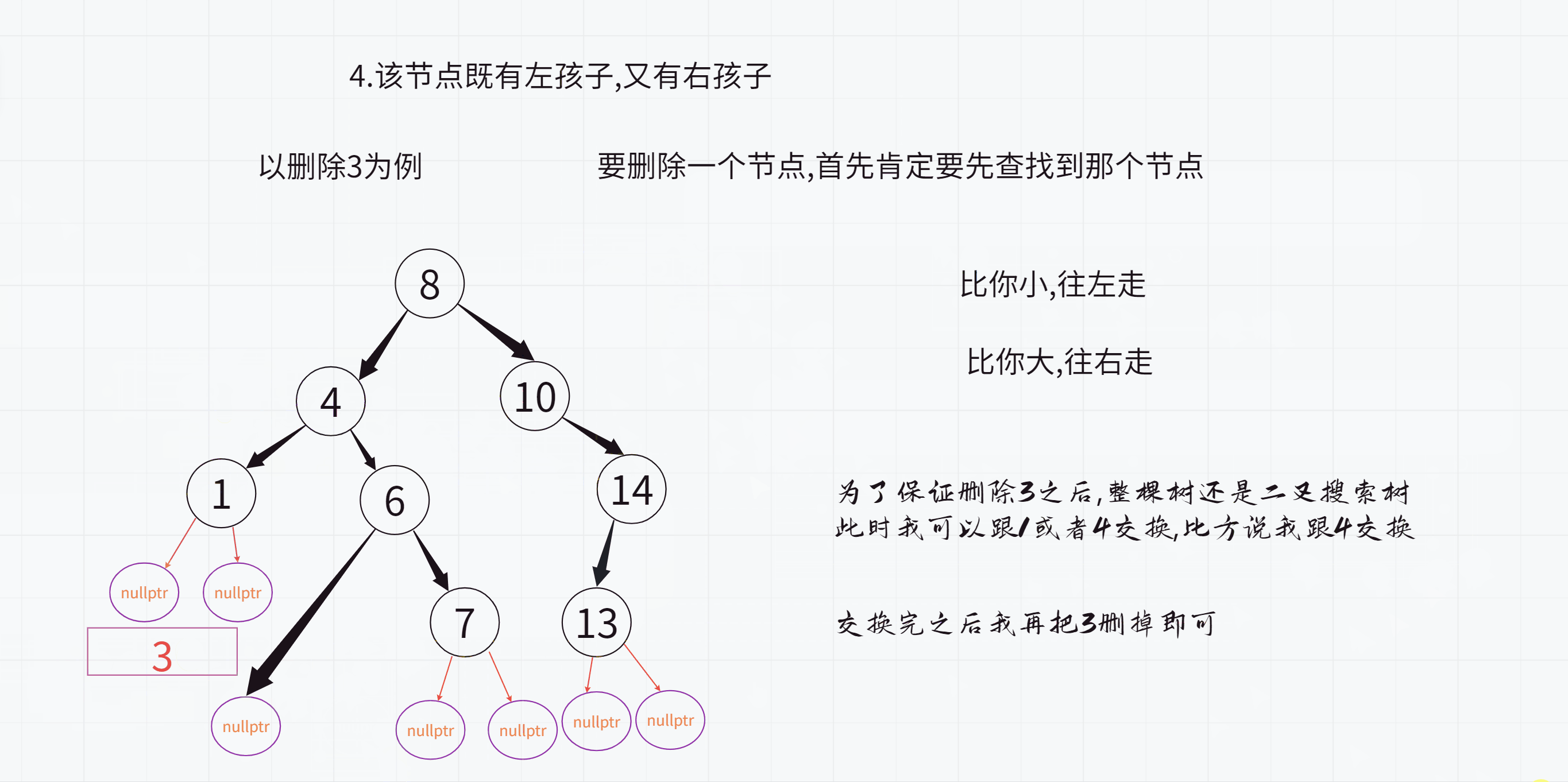
其实这里的1就是整棵树当中小于3这个值的最大值
4就是整棵树当中大于3这个值的最小值
他们都可以来代替3这个值
1其实就是要删除的节点的左子树的最大值(最大值就是最右侧节点)
4其实就是要删除的节点的右子树的最小值(最大值就是最左侧节点)
而且1和4都有一个特点:最多只有一个孩子
此时删除1和4就可以借助于第2种或第3种方案了
我们今天按照寻找右子树的最小值的方式来做
注意:之后删除3的操作不能使用递归,因为交换后就不是二叉搜索树了,就无法保证能够找到那个值了
不过上述的讨论当中我们讨论的都是该节点有父亲的情况
都没有讨论下面的这种情况:
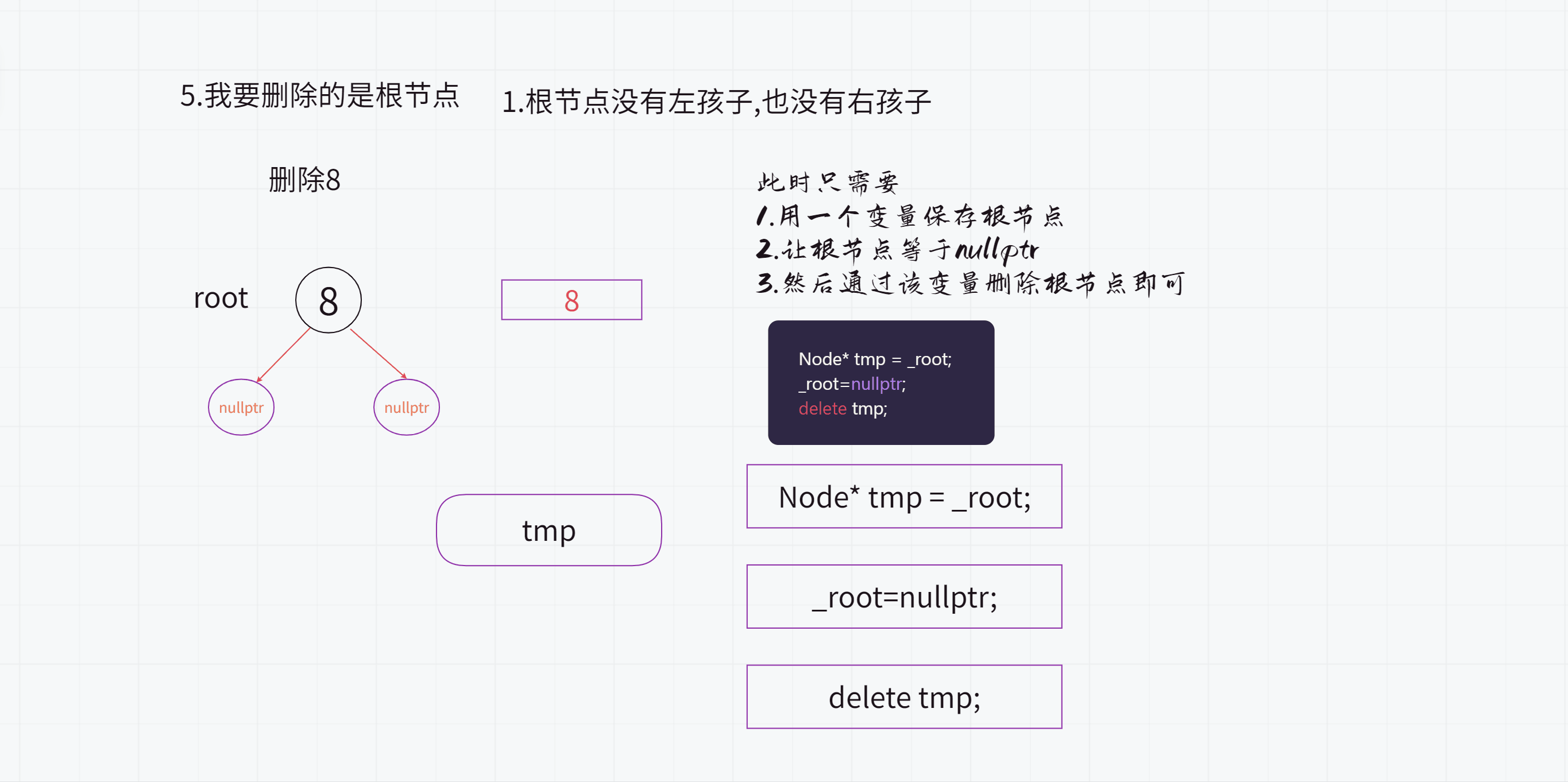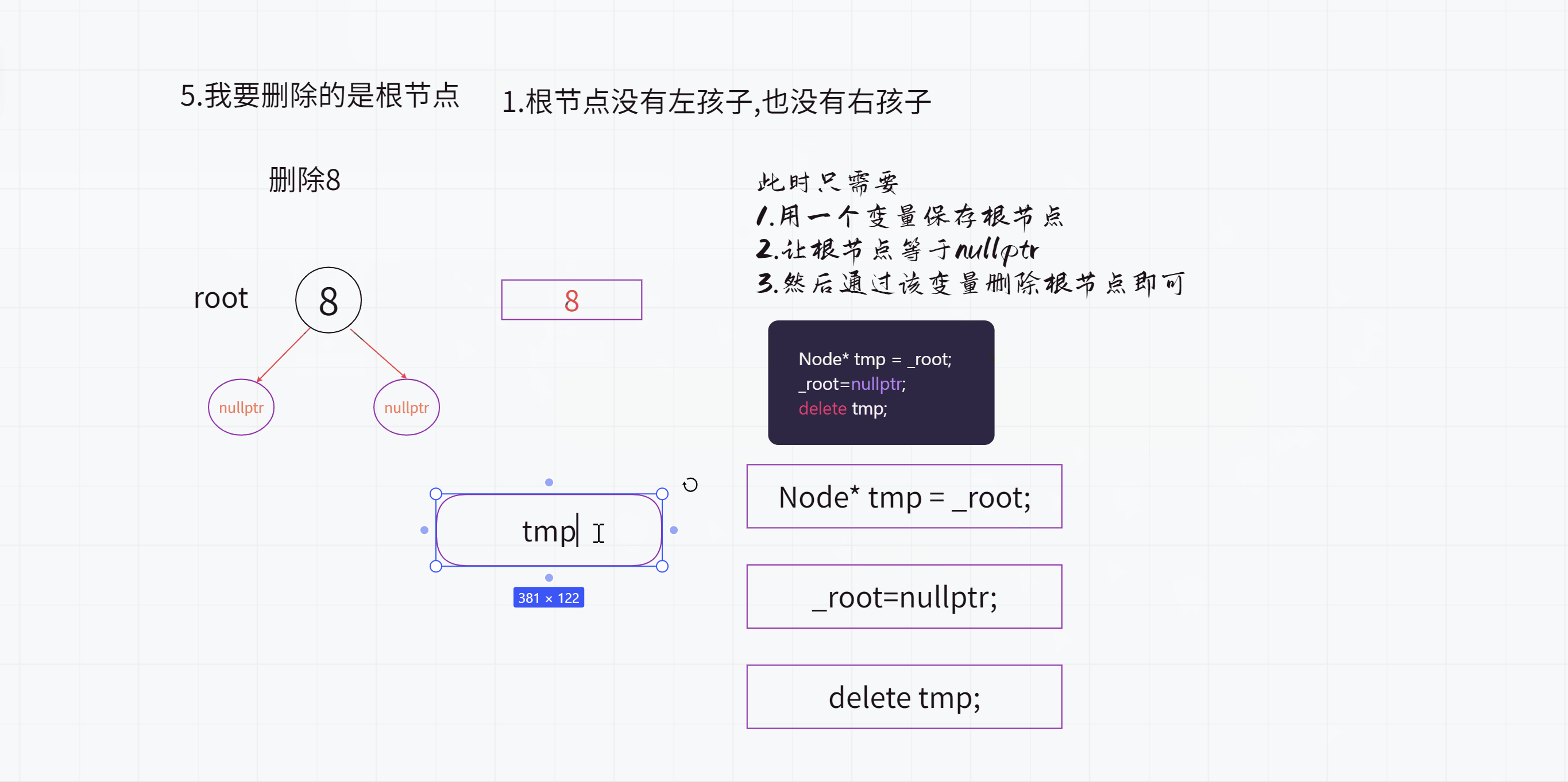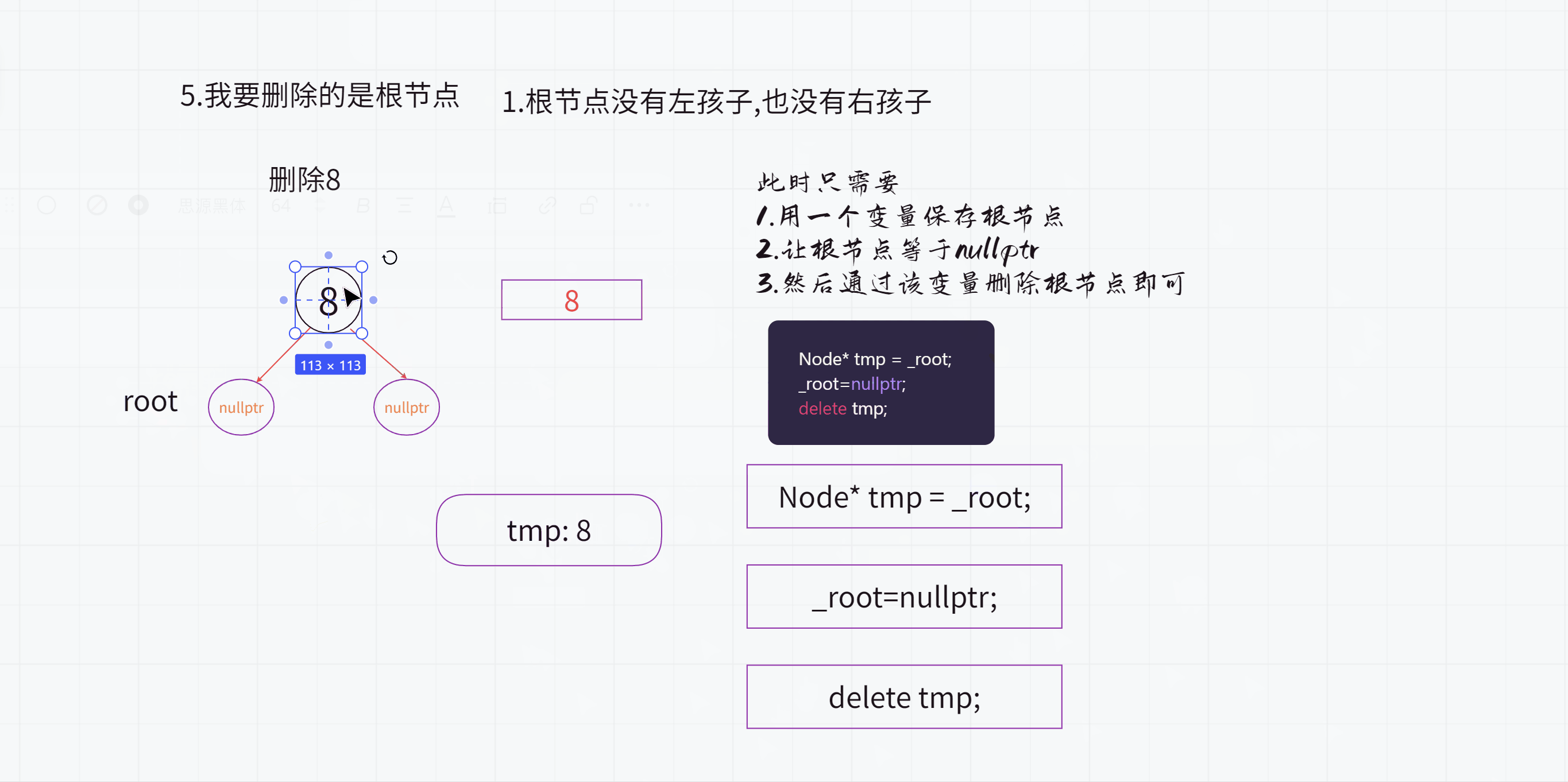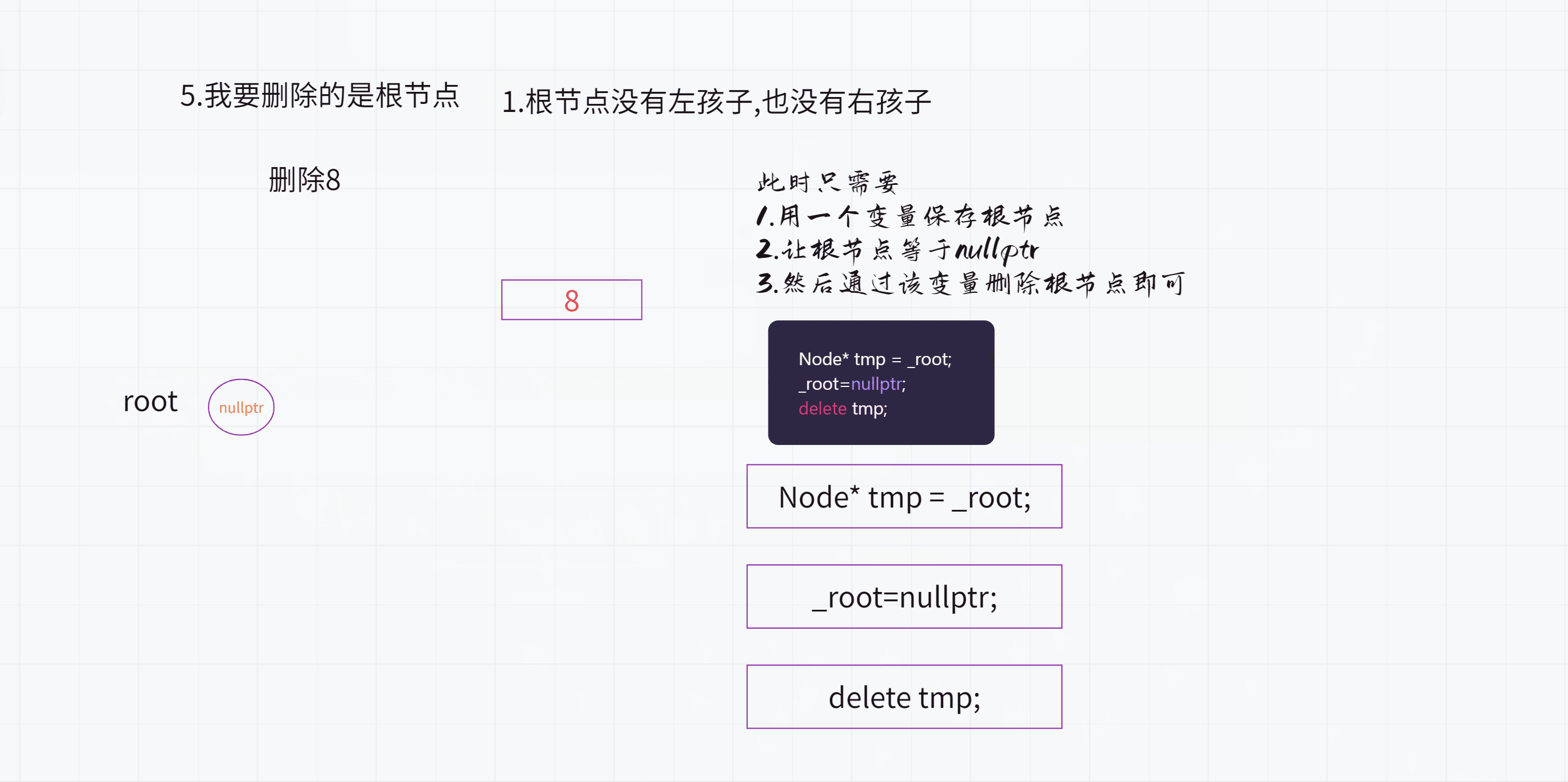
5.我要删除的是根节点呢?
(1).根节点没有左孩子也没有右孩子
Node* tmp = _root;
_root=nullptr;
delete tmp;
(2).根节点只有1个孩子
因为我们知道:一个二叉搜索树的左子树和右子树都是二叉搜索树
比方说根节点只有左孩子,没有右孩子
此时只需要让根节点等于左子树的根节点(也就是根节点的左孩子)即可
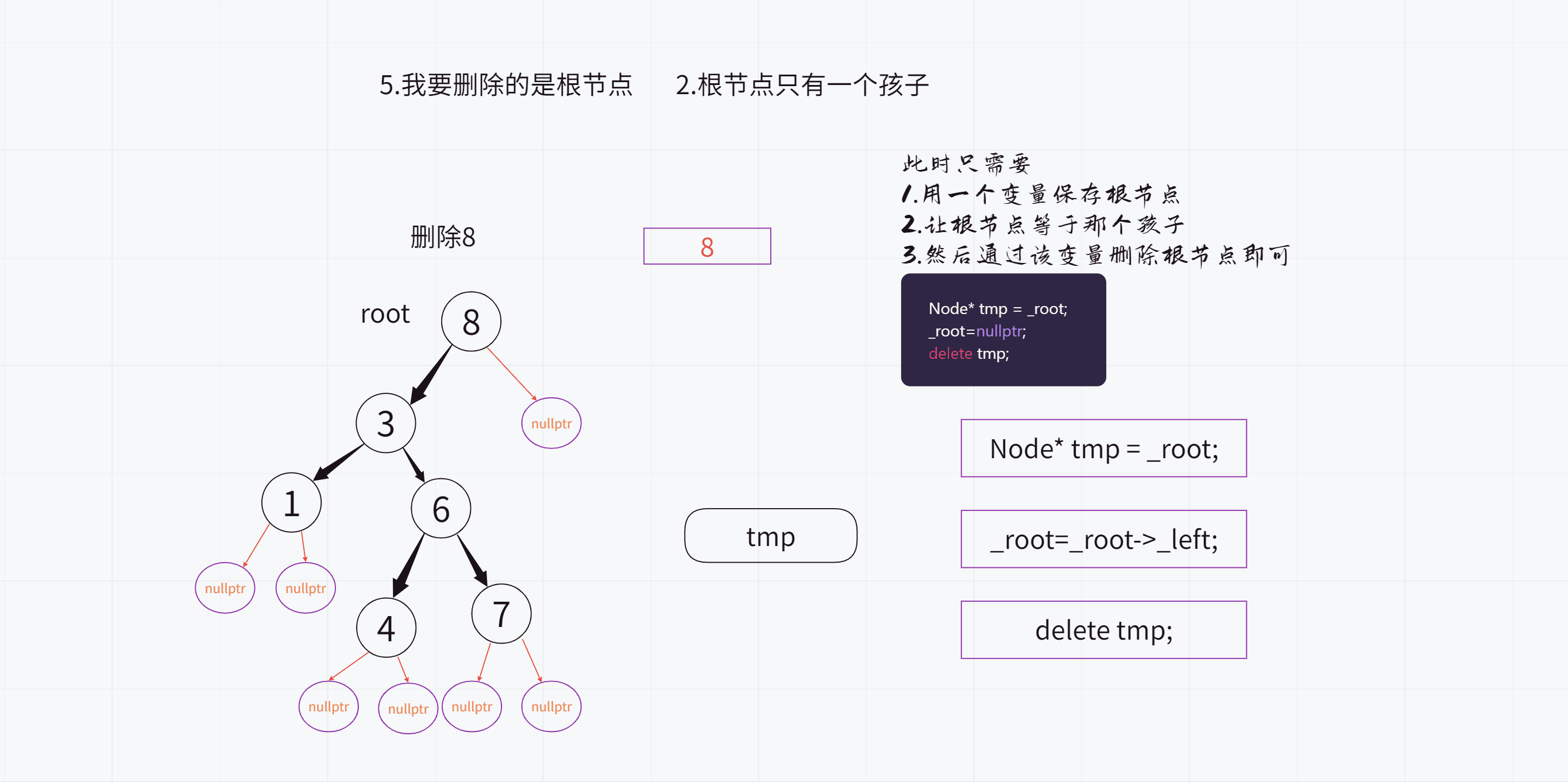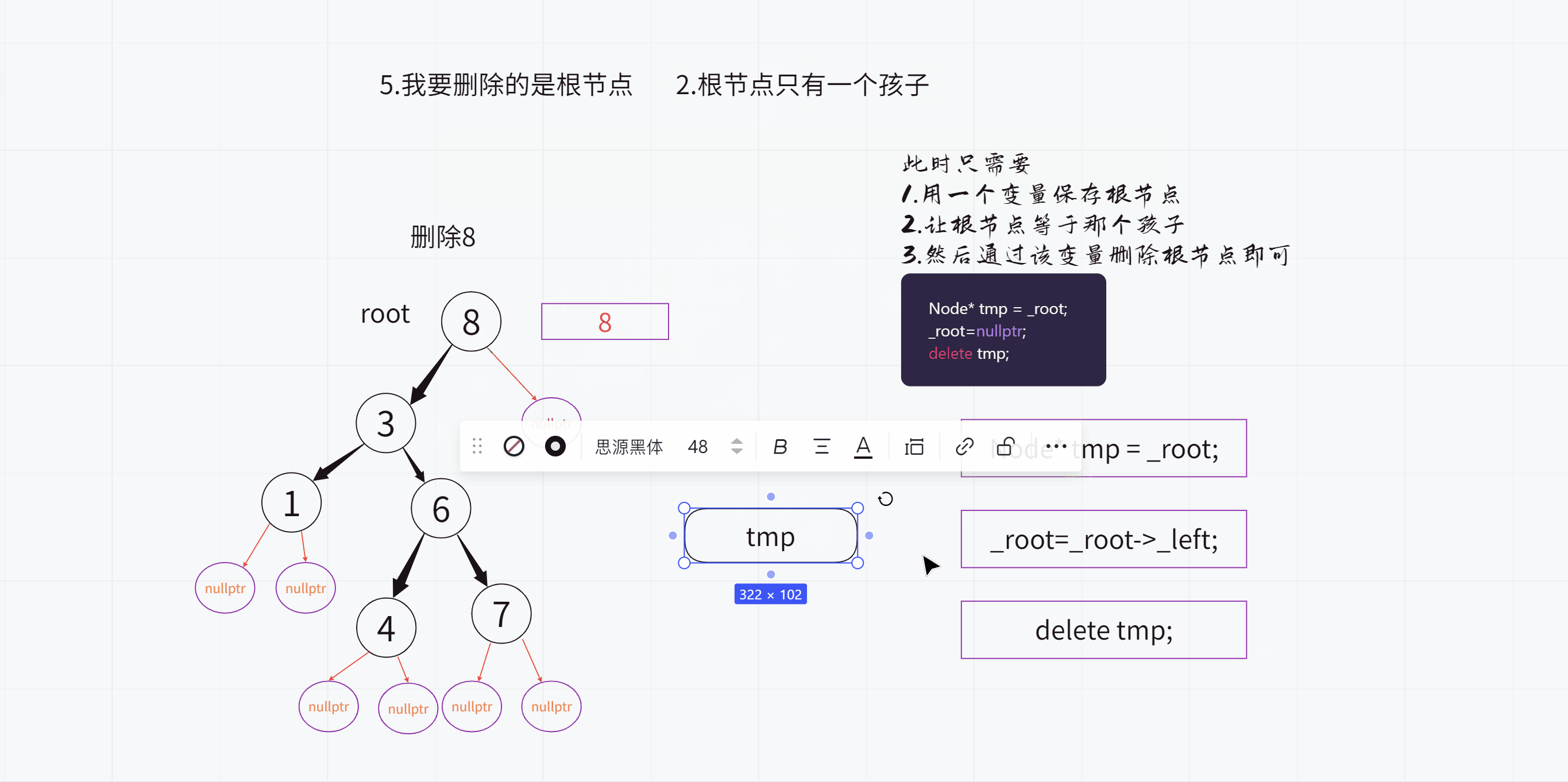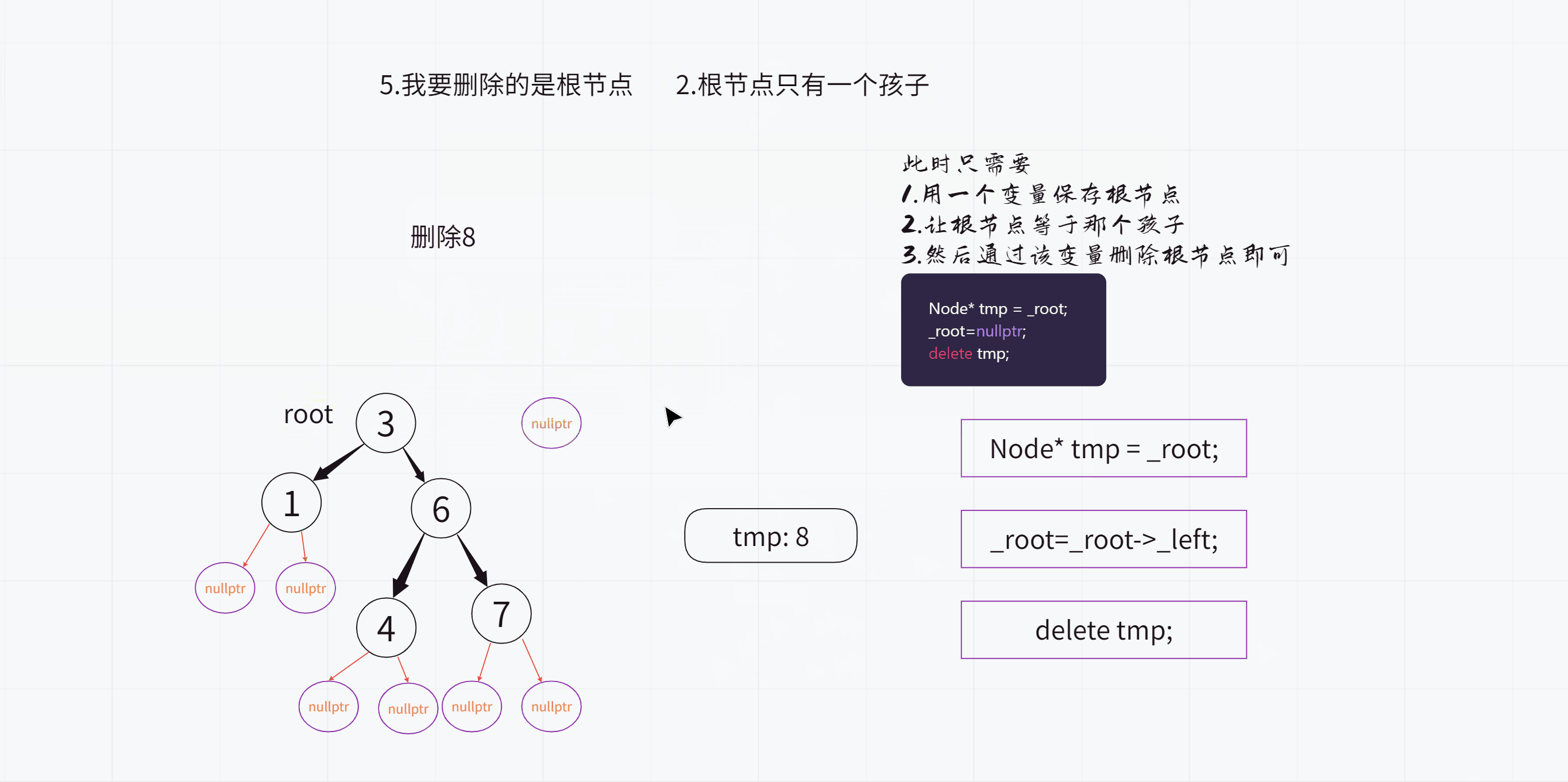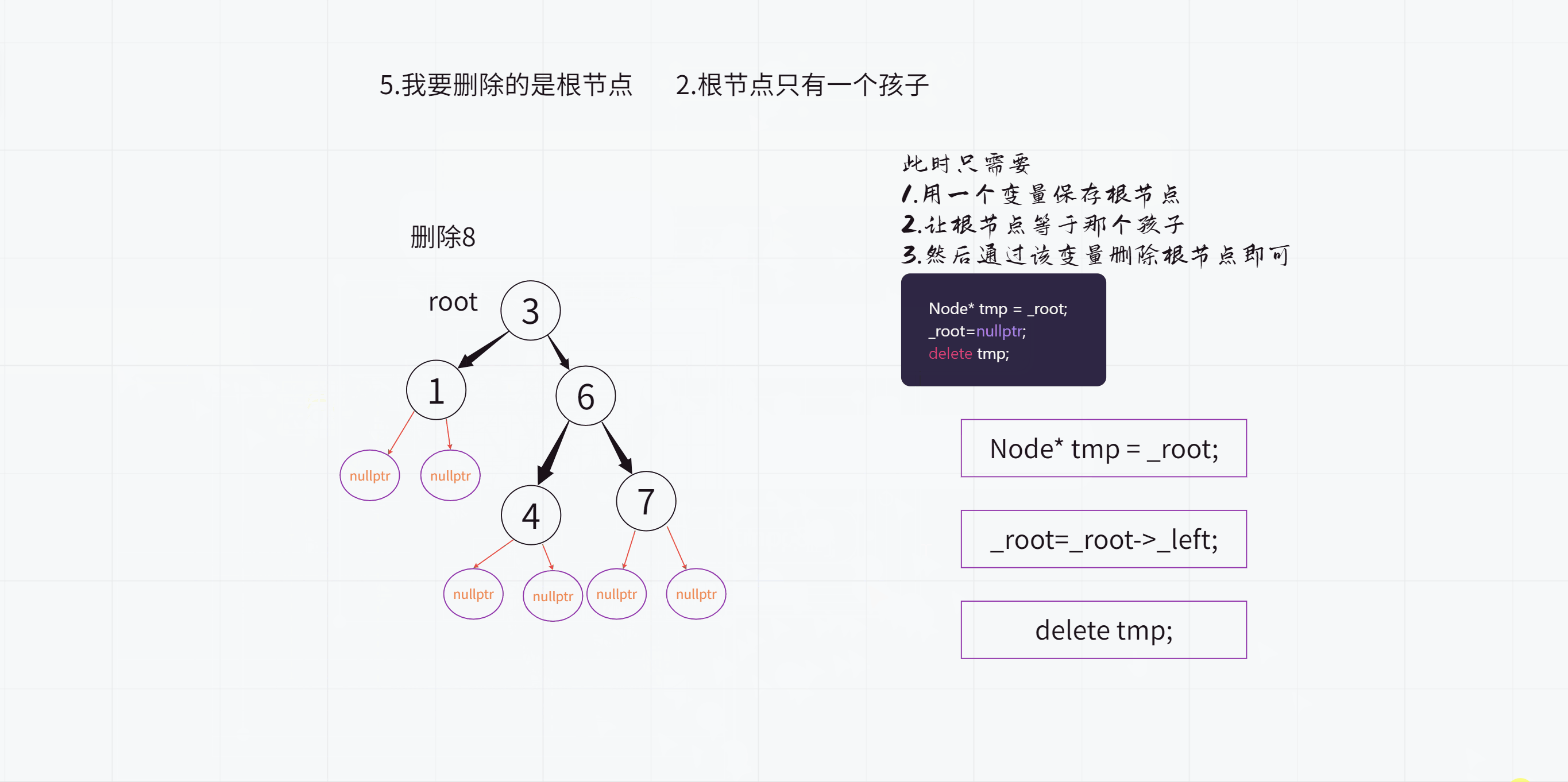
删除根节点之前:
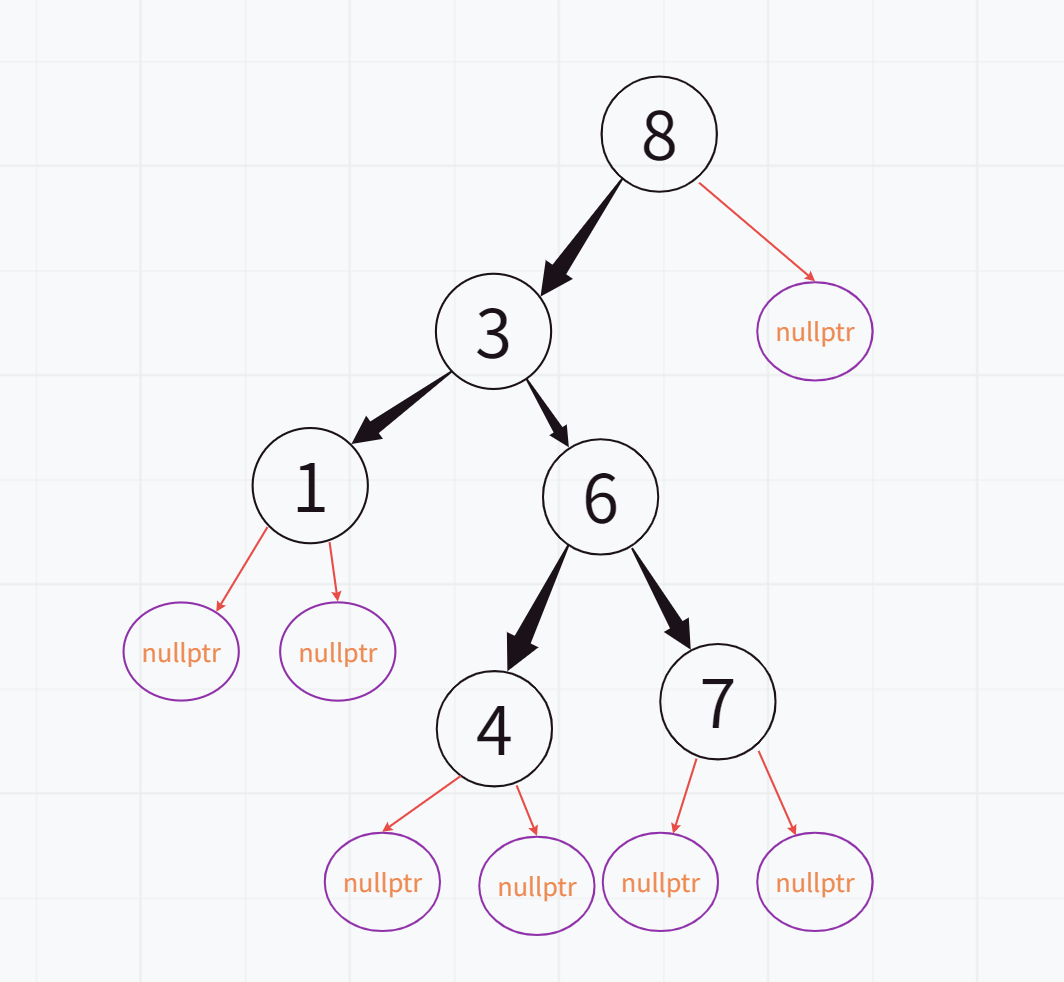
删除根节点之后:

可见,这么做的话,删除之后的确也还是二叉搜索树
同理,节点只有右孩子,没有左孩子的时候
只需要让根节点等于右子树的根节点(也就是根节点的右孩子)即可
同理,第一种情况也可以归为第二种情况
(3).根节点有2个孩子

删除之前:
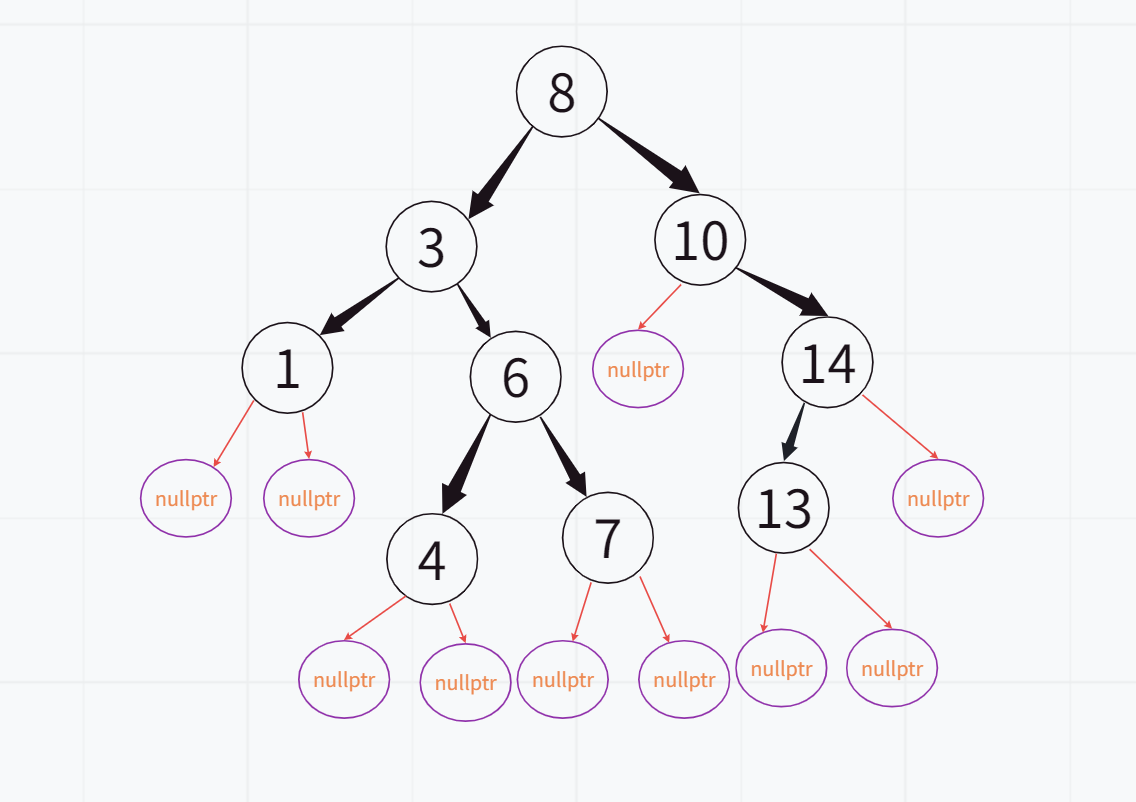
删除之后:
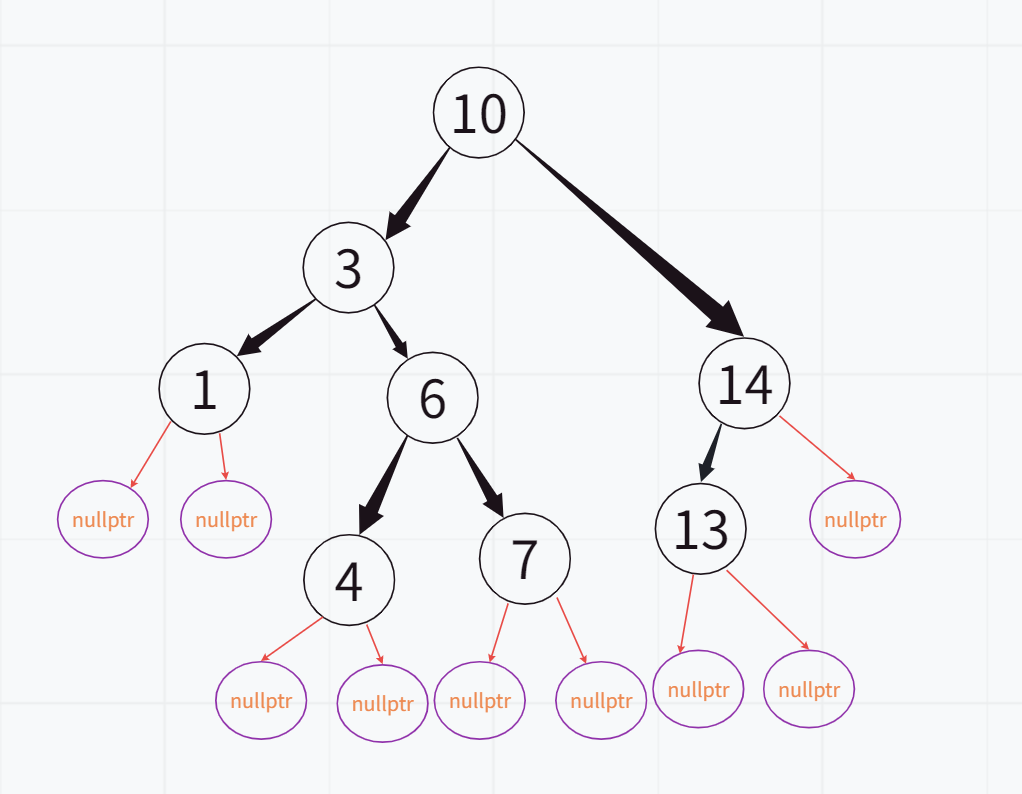
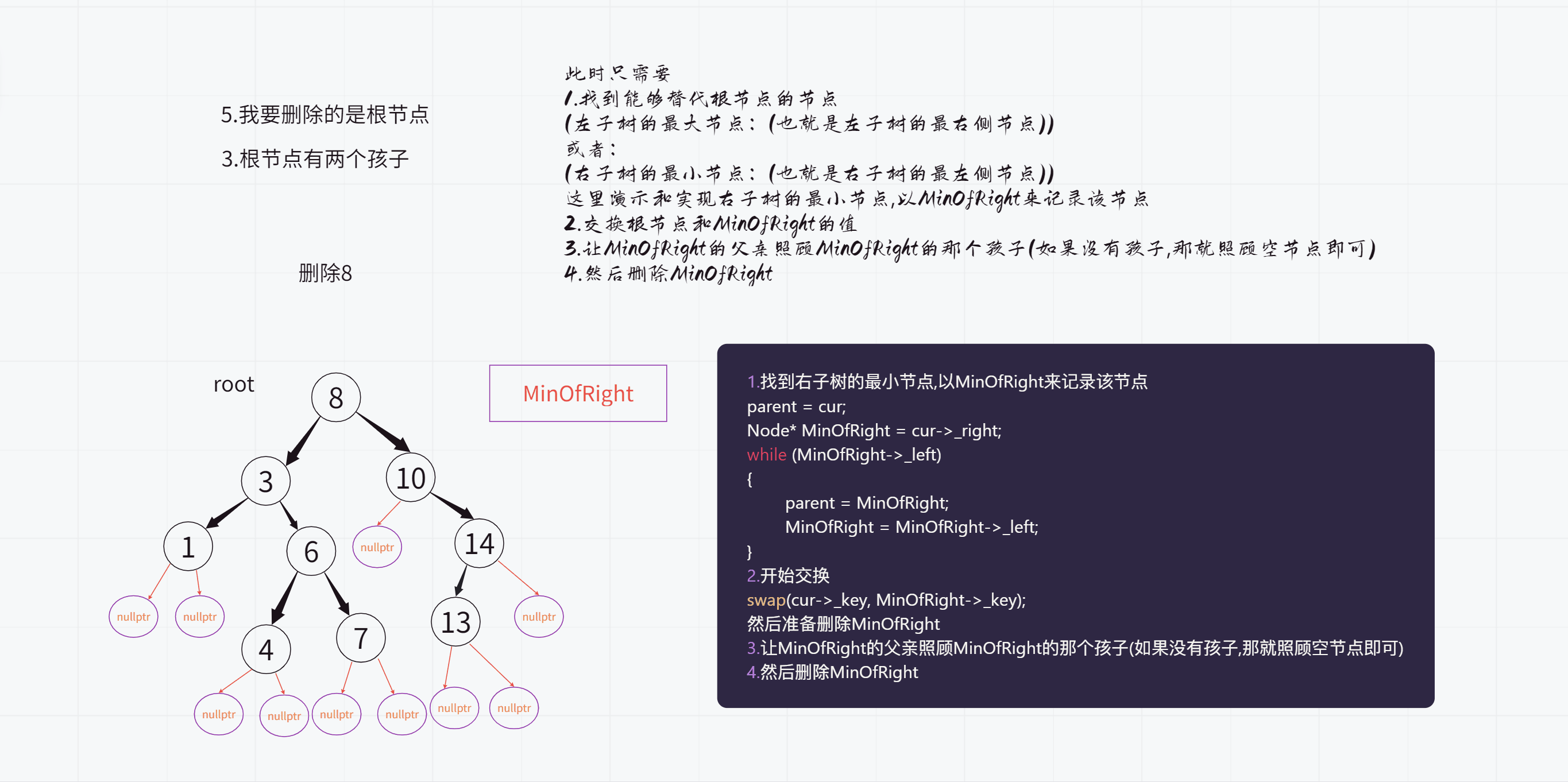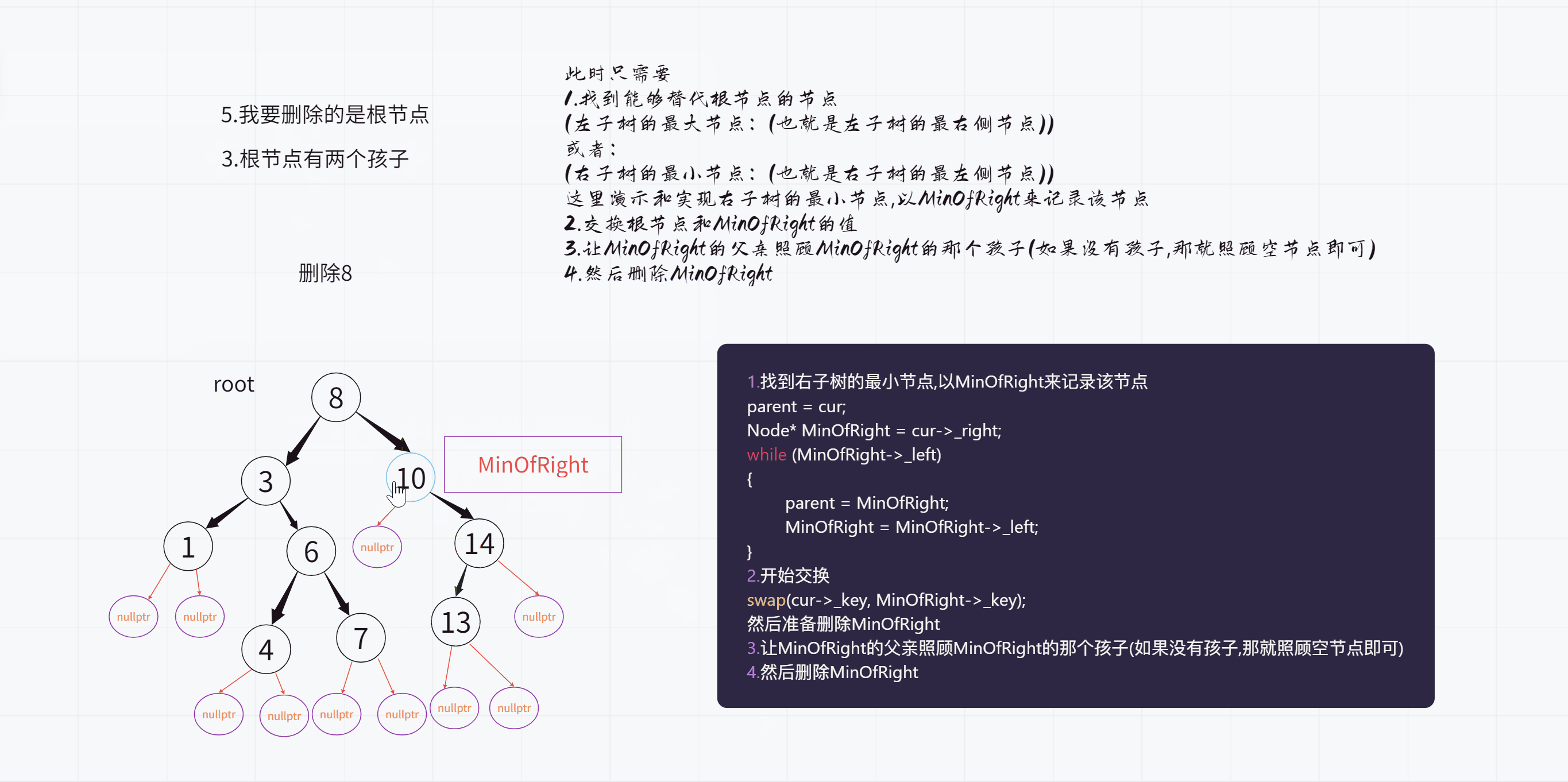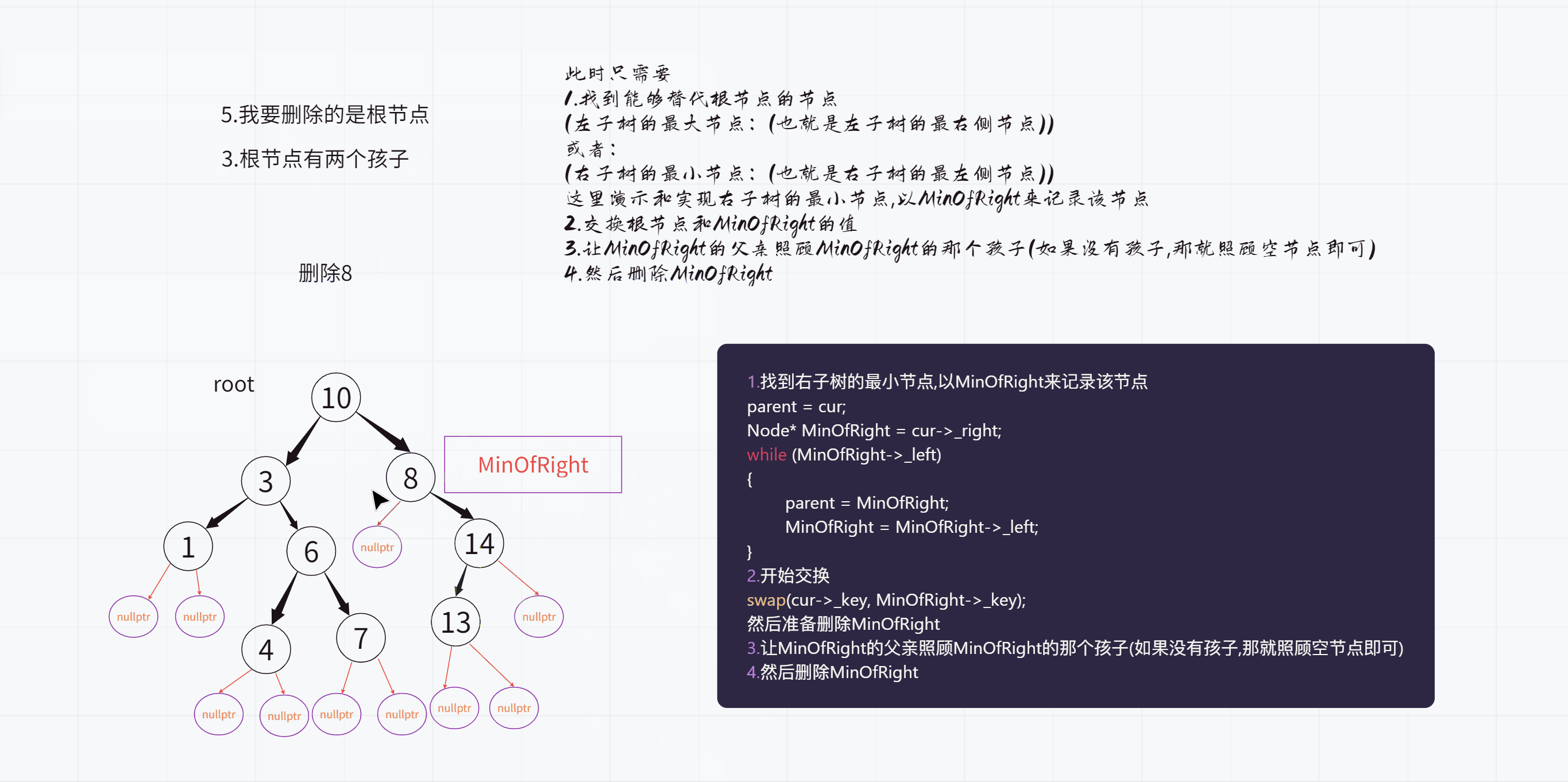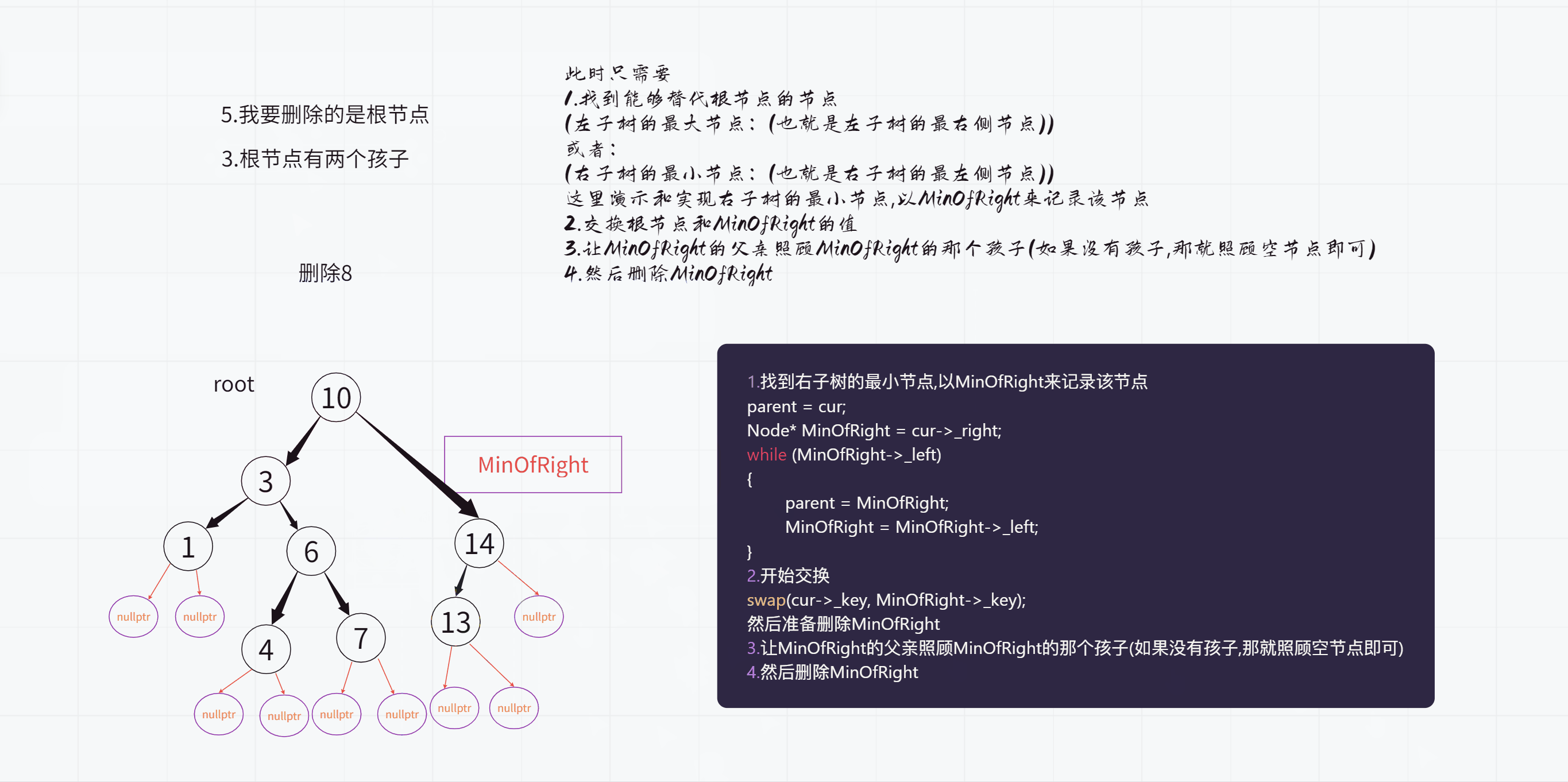
不过这里也分为两种情况
1.因为查找的是右子树的最左侧节点
也就是一路往左查找,因此最后的时候只需要让我的右孩子成为父亲的左孩子即可
2.不过如果没有一路查找,直接找到了的话
也就是说此时我是父亲的右孩子,那么就要让我的右孩子成为父亲的右孩子了
上面演示的那种情况就属于第二种情况
因此,我们就可以写出这样的代码
里面的注释非常详细,大家如果还不是特别理解的话,
可以对照着边走读代码边画图来更好地理解
//删除成功,返回true
//删除失败,说明没有这个元素,返回false
bool Erase(const K& key)
{//1.没有左孩子,没有右孩子 可以归为2,3中的任意一类//2.有右孩子,没有左孩子//3.有左孩子,没有右孩子//4.有左孩子,也有右孩子Node* cur = _root;Node* parent = cur;//父亲while (cur){//往左找if (cur->_key > key){parent = cur;cur = cur->_left;}//往右找else if (cur->_key < key){parent = cur;cur = cur->_right;}//找到了else{//1.有右孩子,没有左孩子//此时只需要让他的右孩子代替它的位置即可(也就是把自己的右孩子给父亲,然后删除自己即可)if (cur->_left == nullptr){//要删除的是_root,且_root没有左孩子//那么让右孩子变成root即可if (cur == _root){_root = cur->_right;delete cur;}//说明我是父亲的左孩子if (cur == parent->_left){//就让我的右孩子成为父亲的左孩子parent->_left = cur->_right;delete cur;}//说明我是父亲的右孩子else{//就让我的右孩子成为父亲的右孩子parent->_right = cur->_right;delete cur;}}//2.有左孩子,没有右孩子else if (cur->_right == nullptr){//要删除的是_root,且_root没有左孩子//那么让右孩子变成root即可if (cur == _root){_root = cur->_left;delete cur;}//说明我是父亲的左孩子if (cur == parent->_left){//就让我的左孩子成为父亲的左孩子parent->_left = cur->_left;delete cur;}//说明我是父亲的右孩子else{//就让我的左孩子成为父亲的右孩子parent->_right = cur->_left;delete cur;}}//3.有左孩子,也有右孩子//我既可以让左子树的最大值替代我,也可以让右子树的最小值替代我//这里就找右子树的最小值吧,右子树的最小值就是右子树的最左侧节点//找到右子树中的最小值,将他的值跟我交换,然后删除刚才那个节点//注意:"删除刚才那个节点"的操作不能使用递归,因为交换后就不是BST了,就无法保证能够找到那个值了else{parent = cur;Node* MinOfRight = cur->_right;while (MinOfRight->_left){parent = MinOfRight;MinOfRight = MinOfRight->_left;}//开始交换swap(cur->_key, MinOfRight->_key);//然后删除MinOfRight//1.的确向下查找了//此时MinOfRight就是parent的左孩子//并且此时MinOfRight没有左孩子,那么就可以直接把MinOfRight的右孩子给parent当做它的左孩子,然后就可以删除了if (parent->_left == MinOfRight){parent->_left = MinOfRight->_right;delete MinOfRight;}//2.没有继续往下查找//此时MinOfRight就是parent的右孩子//并且此时MinOfRight没有左孩子,那么就可以直接把MinOfRight的右孩子给parent当做它的右孩子,然后就可以删除了else{parent->_right = MinOfRight->_right;delete MinOfRight;}}//删除成功return true;}}//此时cur为空说明没有找到return false;
}
六.Find,Insert,Erase的递归版本
1.FindR
Find的递归版本就很简单了:
假设要查找的值是Key
如果当前节点的值==key:查到了,返回当前节点即可
如果当前节点的值>key:说明当前节点值太大,往左找
如果当前节点的值<key:说明当前节点值太小,往右找
Node* FindR(const K& key)
{return _FindR(_root,key);
}
Node* _FindR(Node* root, const K& key)
{if (root == nullptr){return nullptr;}if (root->_key > key){return _FindR(root->_left, key);}else if(root->_key < key){return _FindR(root->_right, key);}else{return root;}
}
2.InsertR
如果当前节点是空节点:说明找到了空位置,插入即可
如果当前节点的值>key:说明当前节点值太大,往左找插入位置
如果当前节点的值<key:说明当前节点值太小,往右找插入位置
如果当前节点的值==key:说明重复了,返回false,不能插入重复元素
bool InsertR(const K& key)
{return _InsertR(_root, key);
}
bool _InsertR(Node*& root, const K& key)
{if (root == nullptr){root = new Node(key);return true;}else if (root->_key > key){return _InsertR(root->_left, key);}else if(root->_key < key){return _InsertR(root->_right, key);}else{return false;}
}
这里特别巧妙的一点在于:只要加上引用
那么就可以不用传递父节点了
因为root就是上一个节点的左孩子或者右孩子的别名,改变root会影响到上一个节点的左孩子或者右孩子
这里引用作为参数的价值就显得格外巧妙了
3.EraseR
这里是递归版本的erase,
而且要删除的节点跟MinOfRight交换之后,右子树是一个二叉搜索树
因此后面删除MinOfRight的时候可以复用,直接在右子树上面删除MinOfRight即可
而且对于删除根节点也是如此
这里依旧使用引用作为参数,它的巧妙之处在于修改指向时特别方便了,无需传入父亲节点
bool EraseR(const K& key)
{return _EraseR(_root, key);
}
bool _EraseR(Node*& root, const K& key)
{if (root == nullptr){return false;}//1.往左找,在左子树里面删除keyif (root->_key > key){return _EraseR(root->_left, key);}//2.往右找,在右子树里面删除keyelse if (root->_key < key){return _EraseR(root->_right, key);}// 当前的根节点else{//root不仅仅是root,root是父亲的孩子的别名//因此只需要改变root就可以改变父亲的孩子了if (root->_left == nullptr){//不要忘了保存rootNode* del = root;root = root->_right;//这里不是迭代,而是修改指向,是把我的右孩子托付给父亲delete del;return true;}else if (root->_right == nullptr){Node* del = root;root = root->_left;delete del;return true;}else{Node* MinOfRight = root->_right;while (MinOfRight->_left){MinOfRight = MinOfRight->_left;}swap(root->_key, MinOfRight->_key);//注意:现在是递归版本,参数可以传入节点,此时这棵树不是BST,但是root的右子树是BST//所以此时递归删除root->_right上的key值即可//而且也适用于直接删除根节点的情况_EraseR(root->_right, key);}}return true;
}
七.析构,拷贝构造,赋值运算符重载
1.析构
跟二叉树的销毁一样,后序遍历销毁
依旧是采用递归版本
//析构函数 后续遍历析构
~BSTree()
{_Destroy(_root);
}
void _Destroy(Node*& root)
{if (root == nullptr) return;_Destroy(root->_left);_Destroy(root->_right);delete root;root = nullptr;
}
2.拷贝构造
先序遍历构造
先构造根节点,然后递归构造左子树和右子树
最后返回根节点
//拷贝构造
//先序遍历构造
BSTree(const BSTree<K>& bst)
{_root = _Copy(bst._root);
}
Node* _Copy(const Node* root)
{if (root == nullptr){return nullptr;}Node* NewRoot = new Node(root->_key);NewRoot->_left = _Copy(root->_left);NewRoot->_right = _Copy(root->_right);return NewRoot;
}
3.赋值运算重载
实现了拷贝构造之后就可以
直接现代写法了
//赋值运算符重载
BSTree<K>& operator=(BSTree<K> bst)
{std::swap(_root, bst._root);return *this;
}
八.Key模型完整代码
template <class K>
struct BSTreeNode
{BSTreeNode<K>* _left = nullptr;BSTreeNode<K>* _right = nullptr;K _key;BSTreeNode(const K& key):_key(key){}
};template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public://非递归实现insert.find,erasebool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* cur = _root;Node* parent = _root;//记录父亲,因为要能够插入while (cur){//要插入的值小于父亲,插入到左子树当中if (cur->_key > key){parent = cur;cur = cur->_left;}//要插入的的值大于父亲,插入到右子树当中else if (cur->_key < key){parent = cur;cur = cur->_right;}//出现了重复元素,BST搜索二叉树不允许出现重复值,因此不允许插入,返回falseelse{return false;}}//此时cur为空,在此位置插入valuecur = new Node(key);//要插入的元素小于父亲,插入到左子树当中if (parent->_key > key){parent->_left = cur;}//要插入的元素大于父亲,插入到右子树当中else{parent->_right = cur;}//插入成功return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else{return cur;}}//此时cur为空说明没有找到return nullptr;}bool Erase(const K& key){//1.没有左孩子,没有右孩子 可以归为2,3中的任意一类//2.有右孩子,没有左孩子//3.有左孩子,没有右孩子//4.有左孩子,也有右孩子Node* cur = _root;Node* parent = cur;//父亲while (cur){//往左找if (cur->_key > key){parent = cur;cur = cur->_left;}//往右找else if (cur->_key < key){parent = cur;cur = cur->_right;}//找到了else{//1.有右孩子,没有左孩子//此时只需要让他的右孩子代替它的位置即可(也就是把自己的右孩子给父亲,然后删除自己即可)if (cur->_left == nullptr){//要删除的是_root,且_root没有左孩子//那么让右孩子变成root即可if (cur == _root){_root = cur->_right;delete cur;}//说明我是父亲的左孩子if (cur == parent->_left){//就让我的右孩子成为父亲的左孩子parent->_left = cur->_right;delete cur;}//说明我是父亲的右孩子else{//就让我的右孩子成为父亲的右孩子parent->_right = cur->_right;delete cur;}}//2.有左孩子,没有右孩子else if (cur->_right == nullptr){//要删除的是_root,且_root没有左孩子//那么让右孩子变成root即可if (cur == _root){_root = cur->_left;delete cur;}//说明我是父亲的左孩子if (cur == parent->_left){//就让我的左孩子成为父亲的左孩子parent->_left = cur->_left;delete cur;}//说明我是父亲的右孩子else{//就让我的左孩子成为父亲的右孩子parent->_right = cur->_left;delete cur;}}//3.有左孩子,也有右孩子//我既可以让左子树的最大值替代我,也可以让右子树的最小值替代我//这里就找右子树的最小值吧,右子树的最小值就是右子树的最左侧节点//找到右子树中的最小值,将他的值跟我交换,然后删除刚才那个节点//注意:"删除刚才那个节点"的操作不能使用递归,因为交换后就不是BST了,就无法保证能够找到那个值了else{parent = cur;Node* MinOfRight = cur->_right;while (MinOfRight->_left){parent = MinOfRight;MinOfRight = MinOfRight->_left;}//开始交换swap(cur->_key, MinOfRight->_key);//然后删除MinOfRight//1.的确向下查找了//此时MinOfRight就是parent的左孩子//并且此时MinOfRight没有左孩子,那么就可以直接把MinOfRight的右孩子给parent当做它的左孩子,然后就可以删除了if (parent->_left == MinOfRight){parent->_left = MinOfRight->_right;delete MinOfRight;}//2.没有继续往下查找//此时MinOfRight就是parent的右孩子//并且此时MinOfRight没有左孩子,那么就可以直接把MinOfRight的右孩子给parent当做它的右孩子,然后就可以删除了else{parent->_right = MinOfRight->_right;delete MinOfRight;}}//删除成功return true;}}//此时cur为空说明没有找到return false;}//析构函数 后续遍历析构~BSTree(){_Destroy(_root);}//C++11新语法BSTree() = default;//强制生成默认构造//拷贝构造//先序遍历构造BSTree(const BSTree<K>& bst){_root = _Copy(bst._root);}//赋值运算符重载BSTree<K>& operator=(BSTree<K> bst){std::swap(_root, bst._root);return *this;}void InOrder(){_InOrder(_root);cout << endl;}//递归实现insert.find,eraseNode* FindR(const K& key){return _FindR(_root,key);}bool InsertR(const K& key){return _InsertR(_root, key);}bool EraseR(const K& key){return _EraseR(_root, key);}
private:Node* _Copy(const Node* root){if (root == nullptr){return nullptr;}Node* NewRoot = new Node(root->_key);NewRoot->_left = _Copy(root->_left);NewRoot->_right = _Copy(root->_right);return NewRoot;}void _Destroy(Node*& root){if (root == nullptr) return;_Destroy(root->_left);_Destroy(root->_right);delete root;root = nullptr;}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}Node* _FindR(Node* root, const K& key){if (root == nullptr){return nullptr;}if (root->_key > key){return _FindR(root->_left, key);}else if(root->_key < key){return _FindR(root->_right, key);}else{return root;}}bool _InsertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}else if (root->_key > key){return _InsertR(root->_left, key);}else if(root->_key < key){return _InsertR(root->_right, key);}else{return false;}}bool _EraseR(Node*& root, const K& key){if (root == nullptr){return false;}//1.往左找if (root->_key > key){return _EraseR(root->_left, key);}//2.往右找else if (root->_key < key){return _EraseR(root->_right, key);}// 删除else{//root不仅仅是root,root是父亲的孩子的别名,让root成为root的右孩子即可if (root->_left == nullptr){Node* del = root;root = root->_right;//这里不是迭代,而是修改指向,托孤delete del;return true;}else if (root->_right == nullptr){Node* del = root;root = root->_left;delete del;return true;}else{Node* MinOfRight = root->_right;while (MinOfRight->_left){MinOfRight = MinOfRight->_left;}swap(root->_key, MinOfRight->_key);//注意:现在是递归版本,参数可以传入节点,此时这棵树不是BST,但是root的右子树是BST//所以此时递归删除root->_right上的key值即可//而且对于直接删除_root也没有任何影响_EraseR(root->_right, key);}}return true;}Node* _root = nullptr;
};
九.二叉搜索树的应用
1.Key模型

2.Key-Value模型

下面我们把刚才Key模型的代码改为Key-Value模型
只需要改一下:
1.BSTreeNode节点
2.insert
3.InOrder的打印即可
其他地方都不需要修改
namespace kv
{template <class K,class V>struct {BSTreeNode<K,V>* _left = nullptr;BSTreeNode<K,V>* _right = nullptr;K _key;V _value;BSTreeNode(const K& key,const V& value):_key(key),_value(value){}};template<class K,class V>class BSTree{typedef BSTreeNode<K,V> Node;public://非递归实现insert.find,erasebool Insert(const K& key,const V& value){if (_root == nullptr){_root = new Node(key,value);return true;}Node* cur = _root;Node* parent = _root;//记录父亲,因为要能够插入while (cur){//要插入的值小于父亲,插入到左子树当中if (cur->_key > key){parent = cur;cur = cur->_left;}//要插入的的值大于父亲,插入到右子树当中else if (cur->_key < key){parent = cur;cur = cur->_right;}//出现了重复元素,BST搜索二叉树不允许出现重复值,因此不允许插入,返回falseelse{return false;}}//此时cur为空,在此位置插入valuecur = new Node(key,value);//要插入的元素小于父亲,插入到左子树当中if (parent->_key > key){parent->_left = cur;}//要插入的元素大于父亲,插入到右子树当中else{parent->_right = cur;}//插入成功return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else{return cur;}}//此时cur为空说明没有找到return nullptr;}bool Erase(const K& key){//1.没有左孩子,没有右孩子 可以归为2,3中的任意一类//2.有右孩子,没有左孩子//3.有左孩子,没有右孩子//4.有左孩子,也有右孩子Node* cur = _root;Node* parent = cur;//父亲while (cur){//往左找if (cur->_key > key){parent = cur;cur = cur->_left;}//往右找else if (cur->_key < key){parent = cur;cur = cur->_right;}//找到了else{//1.有右孩子,没有左孩子//此时只需要让他的右孩子代替它的位置即可(也就是把自己的右孩子给父亲,然后删除自己即可)if (cur->_left == nullptr){//要删除的是_root,且_root没有左孩子//那么让右孩子变成root即可if (cur == _root){_root = cur->_right;delete cur;}//说明我是父亲的左孩子if (cur == parent->_left){//就让我的右孩子成为父亲的左孩子parent->_left = cur->_right;delete cur;}//说明我是父亲的右孩子else{//就让我的右孩子成为父亲的右孩子parent->_right = cur->_right;delete cur;}}//2.有左孩子,没有右孩子else if (cur->_right == nullptr){//要删除的是_root,且_root没有左孩子//那么让右孩子变成root即可if (cur == _root){_root = cur->_left;delete cur;}//说明我是父亲的左孩子if (cur == parent->_left){//就让我的左孩子成为父亲的左孩子parent->_left = cur->_left;delete cur;}//说明我是父亲的右孩子else{//就让我的左孩子成为父亲的右孩子parent->_right = cur->_left;delete cur;}}//3.有左孩子,也有右孩子//我既可以让左子树的最大值替代我,也可以让右子树的最小值替代我//这里就找右子树的最小值吧,右子树的最小值就是右子树的最左侧节点//找到右子树中的最小值,将他的值跟我交换,然后删除刚才那个节点//注意:"删除刚才那个节点"的操作不能使用递归,因为交换后就不是BST了,就无法保证能够找到那个值了else{parent = cur;Node* MinOfRight = cur->_right;while (MinOfRight->_left){parent = MinOfRight;MinOfRight = MinOfRight->_left;}//开始交换swap(cur->_key, MinOfRight->_key);//然后删除MinOfRight//1.的确向下查找了//此时MinOfRight就是parent的左孩子//并且此时MinOfRight没有左孩子,那么就可以直接把MinOfRight的右孩子给parent当做它的左孩子,然后就可以删除了if (parent->_left == MinOfRight){parent->_left = MinOfRight->_right;delete MinOfRight;}//2.没有继续往下查找//此时MinOfRight就是parent的右孩子//并且此时MinOfRight没有左孩子,那么就可以直接把MinOfRight的右孩子给parent当做它的右孩子,然后就可以删除了else{parent->_right = MinOfRight->_right;delete MinOfRight;}}//删除成功return true;}}//此时cur为空说明没有找到return false;}//析构函数 后续遍历析构~BSTree(){_Destroy(_root);}//C++11新语法BSTree() = default;//强制生成默认构造//拷贝构造//先序遍历构造BSTree(const BSTree<K,V>& bst){_root = _Copy(bst._root);}//赋值运算符重载BSTree<K,V>& operator=(BSTree<K,V> bst){std::swap(_root, bst._root);return *this;}void InOrder(){_InOrder(_root);cout << endl;}//递归实现insert.find,eraseNode* FindR(const K& key){return _FindR(_root, key);}bool InsertR(const K& key,const V& value){return _InsertR(_root, key,value);}bool EraseR(const K& key){return _EraseR(_root, key);}private:Node* _Copy(const Node* root){if (root == nullptr){return nullptr;}Node* NewRoot = new Node(root->_key);NewRoot->_left = _Copy(root->_left);NewRoot->_right = _Copy(root->_right);return NewRoot;}void _Destroy(Node*& root){if (root == nullptr) return;_Destroy(root->_left);_Destroy(root->_right);delete root;root = nullptr;}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << ":" << root->_value << " ";_InOrder(root->_right);}Node* _FindR(Node* root, const K& key){if (root == nullptr){return nullptr;}if (root->_key > key){return _FindR(root->_left, key);}else if (root->_key < key){return _FindR(root->_right, key);}else{return root;}}bool _InsertR(Node*& root, const K& key,const V& value){if (root == nullptr){root = new Node(key,value);return true;}else if (root->_key > key){return _InsertR(root->_left, key);}else if (root->_key < key){return _InsertR(root->_right, key);}else{return false;}}bool _EraseR(Node*& root, const K& key){if (root == nullptr){return false;}//1.往左找if (root->_key > key){return _EraseR(root->_left, key);}//2.往右找else if (root->_key < key){return _EraseR(root->_right, key);}// 删除else{//root不仅仅是root,root是父亲的孩子的别名,让root成为root的右孩子即可if (root->_left == nullptr){Node* del = root;root = root->_right;//这里不是迭代,而是修改指向,托孤delete del;return true;}else if (root->_right == nullptr){Node* del = root;root = root->_left;delete del;return true;}else{Node* MinOfRight = root->_right;while (MinOfRight->_left){MinOfRight = MinOfRight->_left;}swap(root->_key, MinOfRight->_key);//注意:现在是递归版本,参数可以传入节点,此时这棵树不是BST,但是root的右子树是BST//所以此时递归删除root->_right上的key值即可//而且对于直接删除_root也没有任何影响_EraseR(root->_right, key);}}return true;}Node* _root = nullptr;};
}
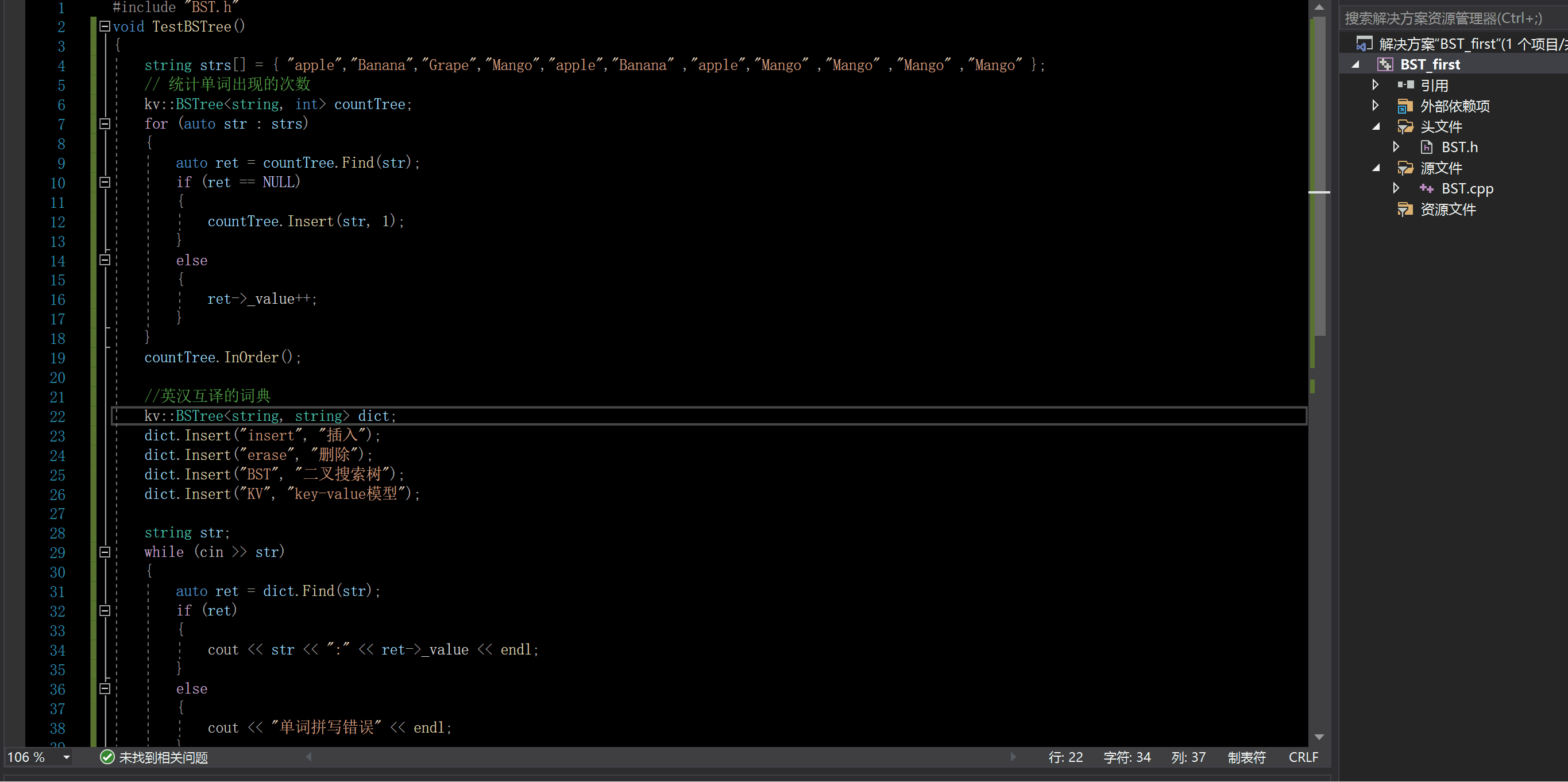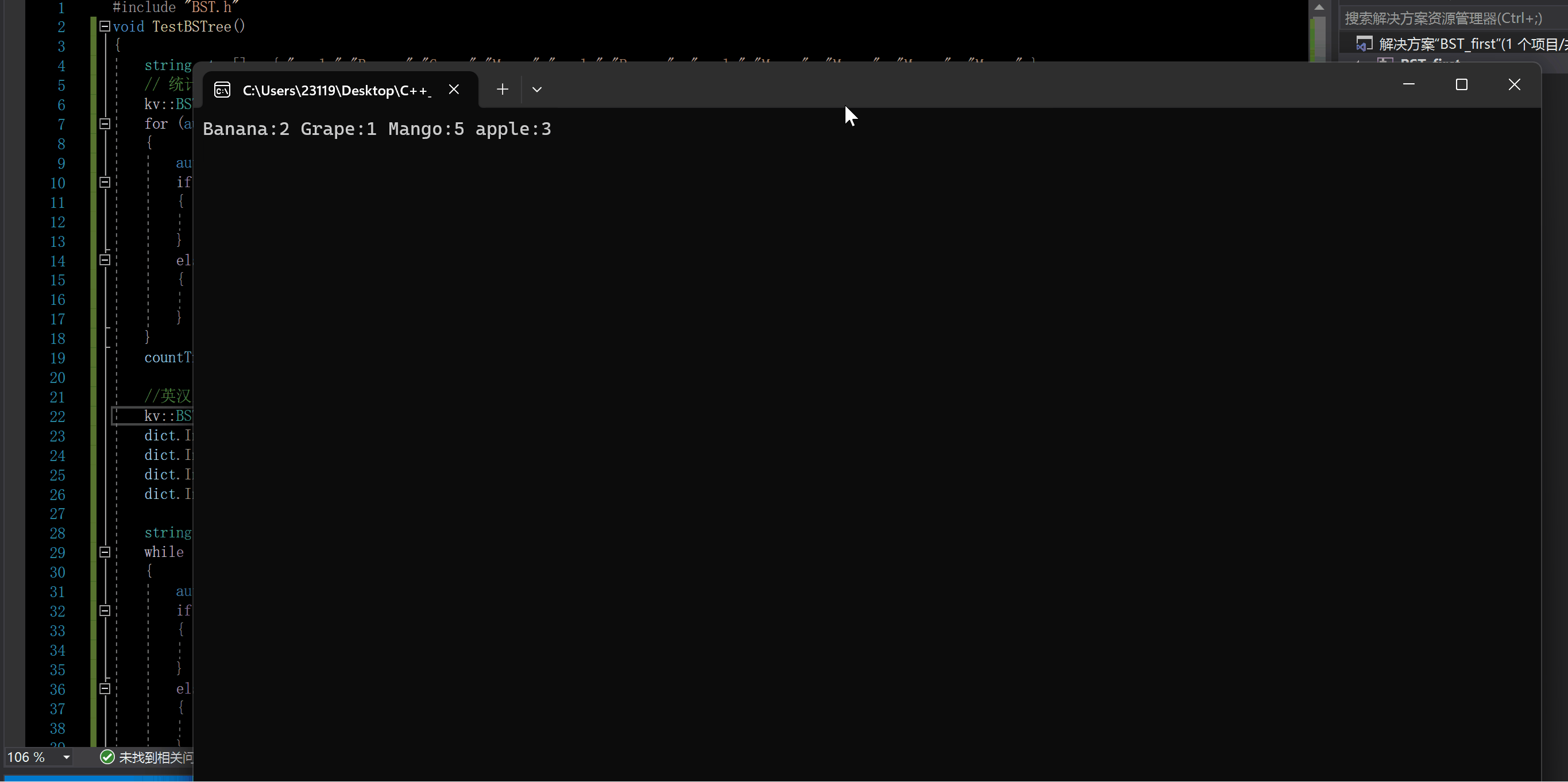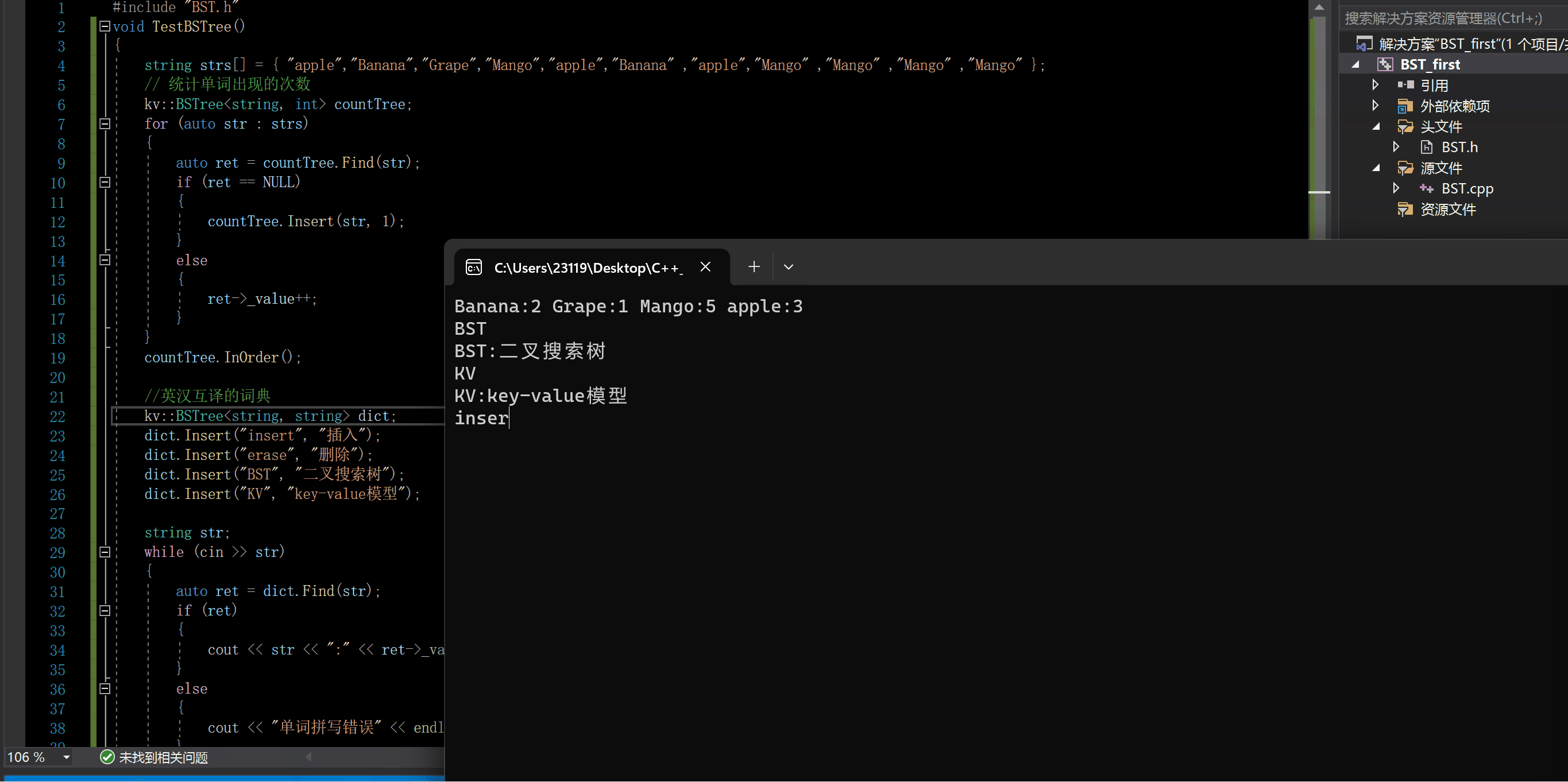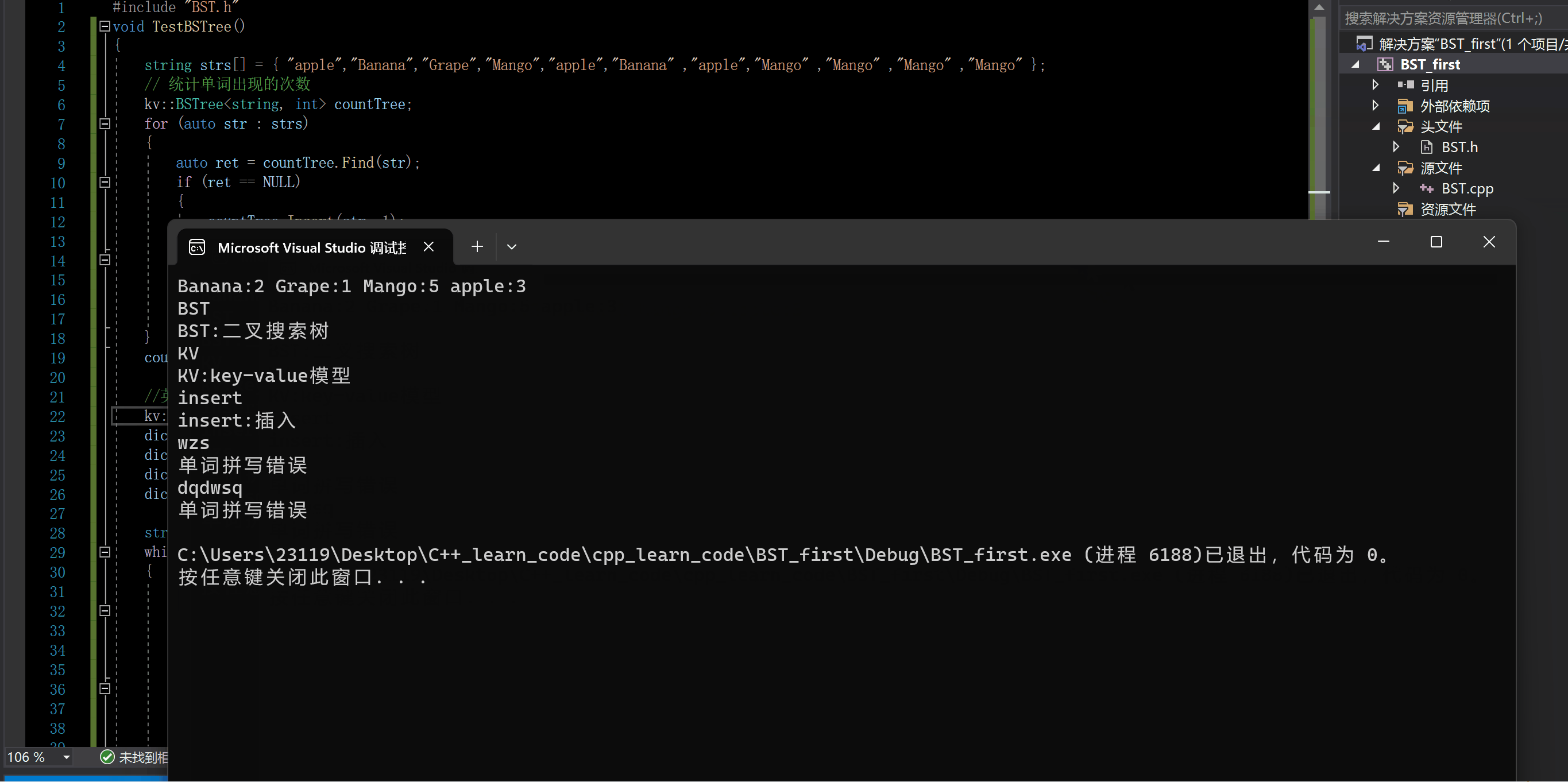
下面我们来测试一下
一个是统计单词出现的次数
一个是英汉互译的词典
void TestBSTree()
{string strs[] = { "apple","Banana","Grape","Mango","apple","Banana" ,"apple","Mango" ,"Mango" ,"Mango" ,"Mango" };// 统计单词出现的次数kv::BSTree<string, int> countTree;for (auto str : strs){auto ret = countTree.Find(str);if (ret == NULL){countTree.Insert(str, 1);}else{ret->_value++;}}countTree.InOrder();//英汉互译的词典kv::BSTree<string, string> dict;dict.Insert("insert", "插入");dict.Insert("erase", "删除");dict.Insert("BST", "二叉搜索树");dict.Insert("KV", "key-value模型");string str;while (cin >> str){auto ret = dict.Find(str);if (ret){cout << str << ":" << ret->_value << endl;}else{cout << "单词拼写错误" << endl;}}
}
以上就是C++ 二叉搜索树(BST)的实现(非递归版本与递归版本)与应用的全部内容,希望能对大家有所帮助!
相关文章:

C++ 二叉搜索树(BST)的实现(非递归版本与递归版本)与应用
C 二叉搜索树的实现与应用 一.二叉搜索树的特点二.我们要实现的大致框架三.Insert四.InOrder和Find1.InOrder2.Find 五.Erase六.Find,Insert,Erase的递归版本1.FindR2.InsertR3.EraseR 七.析构,拷贝构造,赋值运算符重载1.析构2.拷贝构造3.赋值运算重载 八.Key模型完整代码九.二…...
分类预测 | Matlab实现AOA-SVM算术优化支持向量机的数据分类预测【23年新算法】
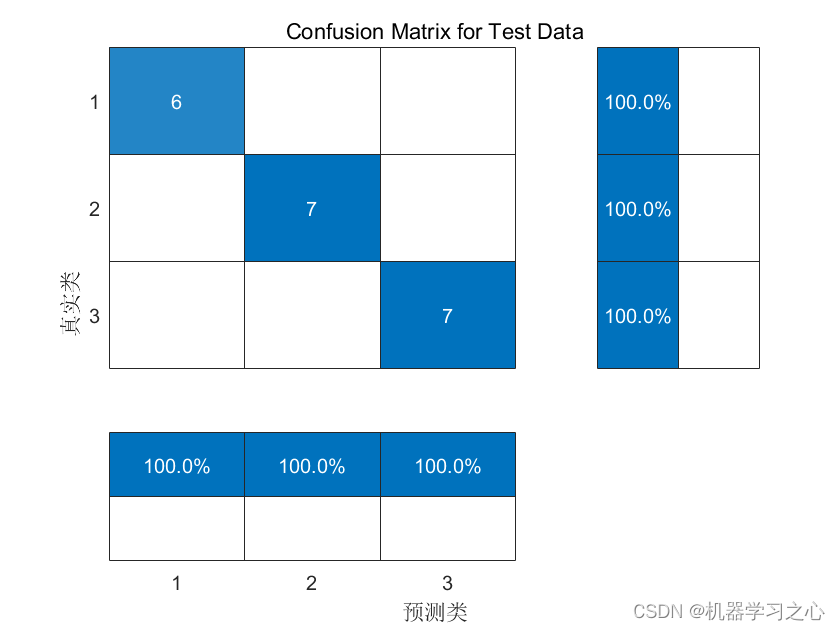
分类预测 | Matlab实现AOA-SVM算术优化支持向量机的数据分类预测【23年新算法】 目录 分类预测 | Matlab实现AOA-SVM算术优化支持向量机的数据分类预测【23年新算法】分类效果基本描述程序设计参考资料 分类效果 基本描述 1.Matlab实现AOA-SVM算术优化支持向量机的数据分类预测…...

代码随想录算法训练营第七天 | 454.四数相加II、383. 赎金信、15. 三数之和 、18. 四数之和
454.四数相加II 题目链接:454.四数相加II 给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足: 0 < i, j, k, l < nnums1[i] nums2[j] nums3[k] nums4[l] 0…...
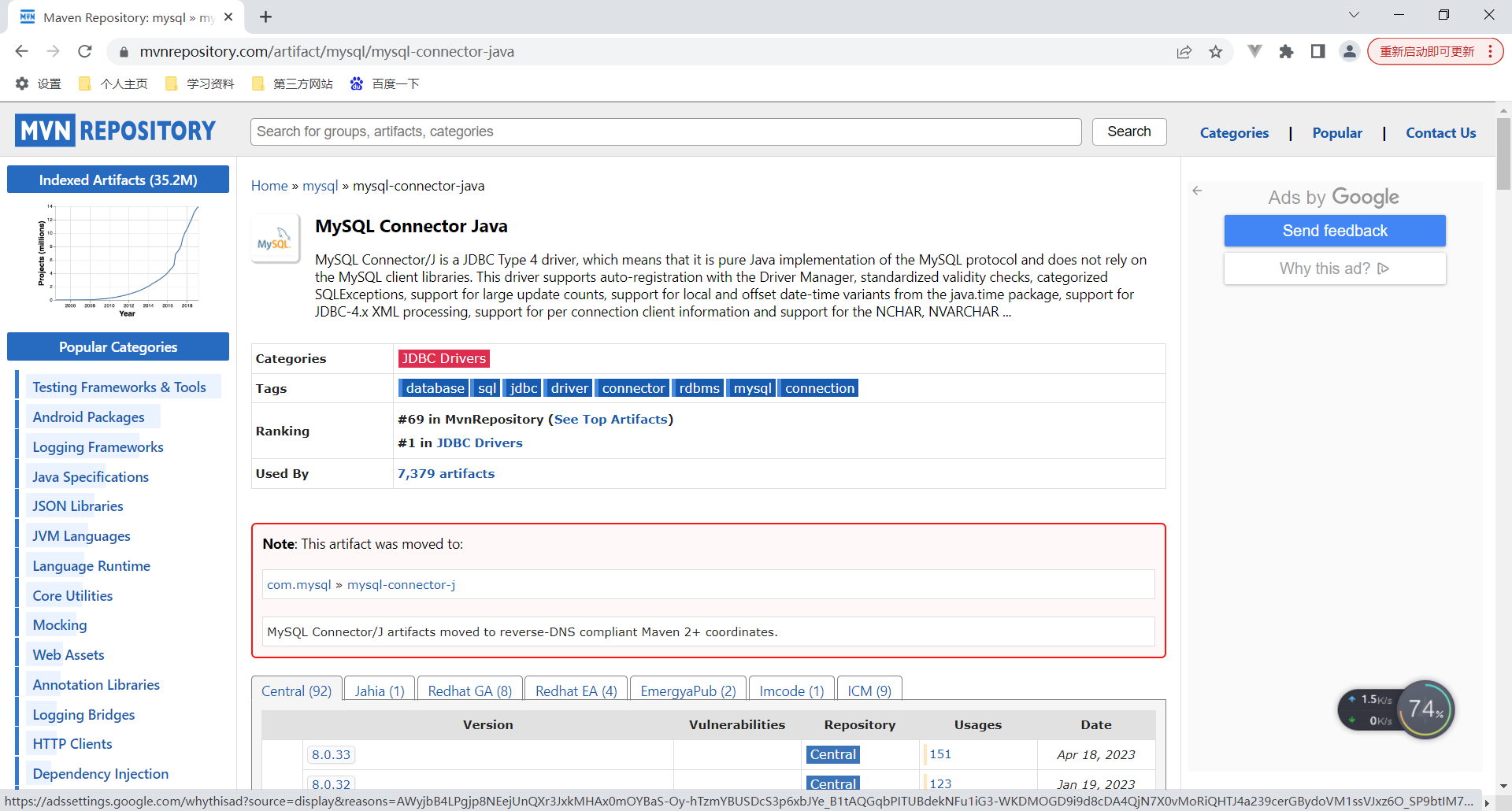
SpringBoot 3.2.0 版本 mysql 依赖下载错误
最近想尝试一下最新的 SpringBoot 项目,于是将自己的开源项目进行了一些升级。 JDK 版本从 JDK8 升级至 JDK17。SpringBoot 版本从 SpringBoot 2.7.3 升级到 SpringBoot 3.2.0 其中 JDK 的升级比较顺利,毕竟 JDK 的旧版本兼容性一直非常好。 但是在升级…...
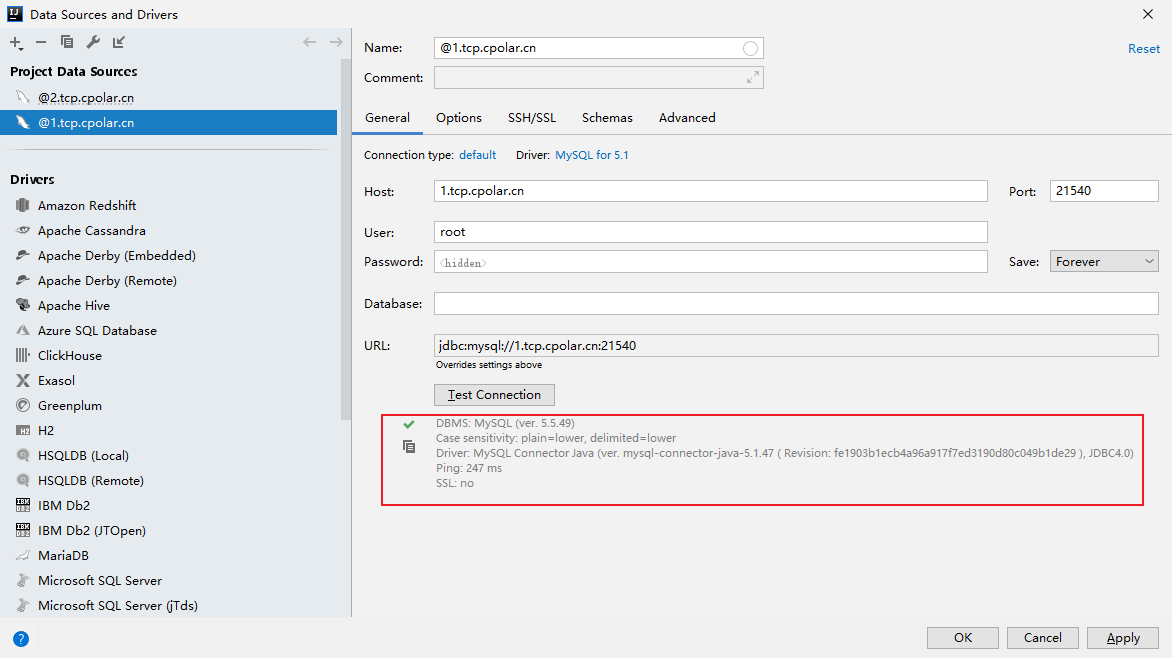
内网穿透的应用-如何结合Cpolar内网穿透工具实现在IDEA中远程访问家里或者公司的数据库
文章目录 1. 本地连接测试2. Windows安装Cpolar3. 配置Mysql公网地址4. IDEA远程连接Mysql小结 5. 固定连接公网地址6. 固定地址连接测试 IDEA作为Java开发最主力的工具,在开发过程中需要经常用到数据库,如Mysql数据库,但是在IDEA中只能连接本…...
ElasticSearch单机或集群未授权访问漏洞
漏洞处理方法: 1、可以使用系统防火墙 来做限制只允许ES集群和Server节点的IP来访问漏洞节点的9200端口,其他的全部拒绝。 2、在ES节点上设置用户密码 漏洞现象:直接访问9200端口不需要密码验证 修复过程 2.1 生成认证文件 必须要生成…...

【华为OD题库-097】最大岛屿体积-java
题目 题目描述 给你一个由大于0的数(陆地)和0(水)组成的的二维网格,请你计算网格中最大岛屿的体积。陆地的数表示所在岛屿的体积。岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。 此外,你可以假…...
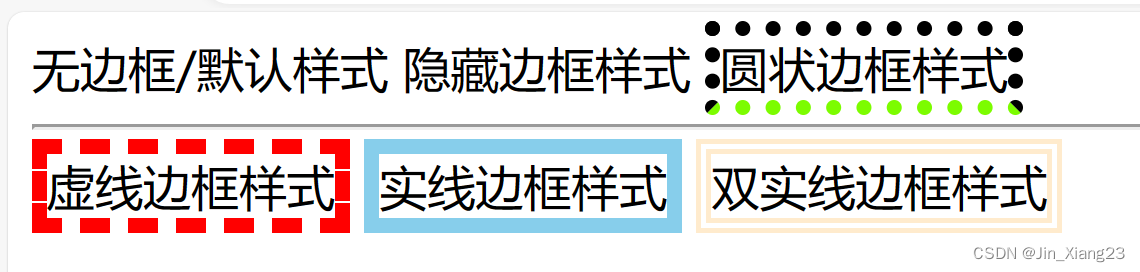
HTML中边框样式、内外边距、盒子模型尺寸计算(附代码图文示例)【详解】
Hi i,m JinXiang ⭐ 前言 ⭐ 本篇文章主要介绍HTML中边框样式、内外边距、盒子模型尺寸计算以及部分理论知识 🍉欢迎点赞 👍 收藏 ⭐留言评论 📝私信必回哟😁 🍉博主收将持续更新学习记录获,友友们有任何问…...
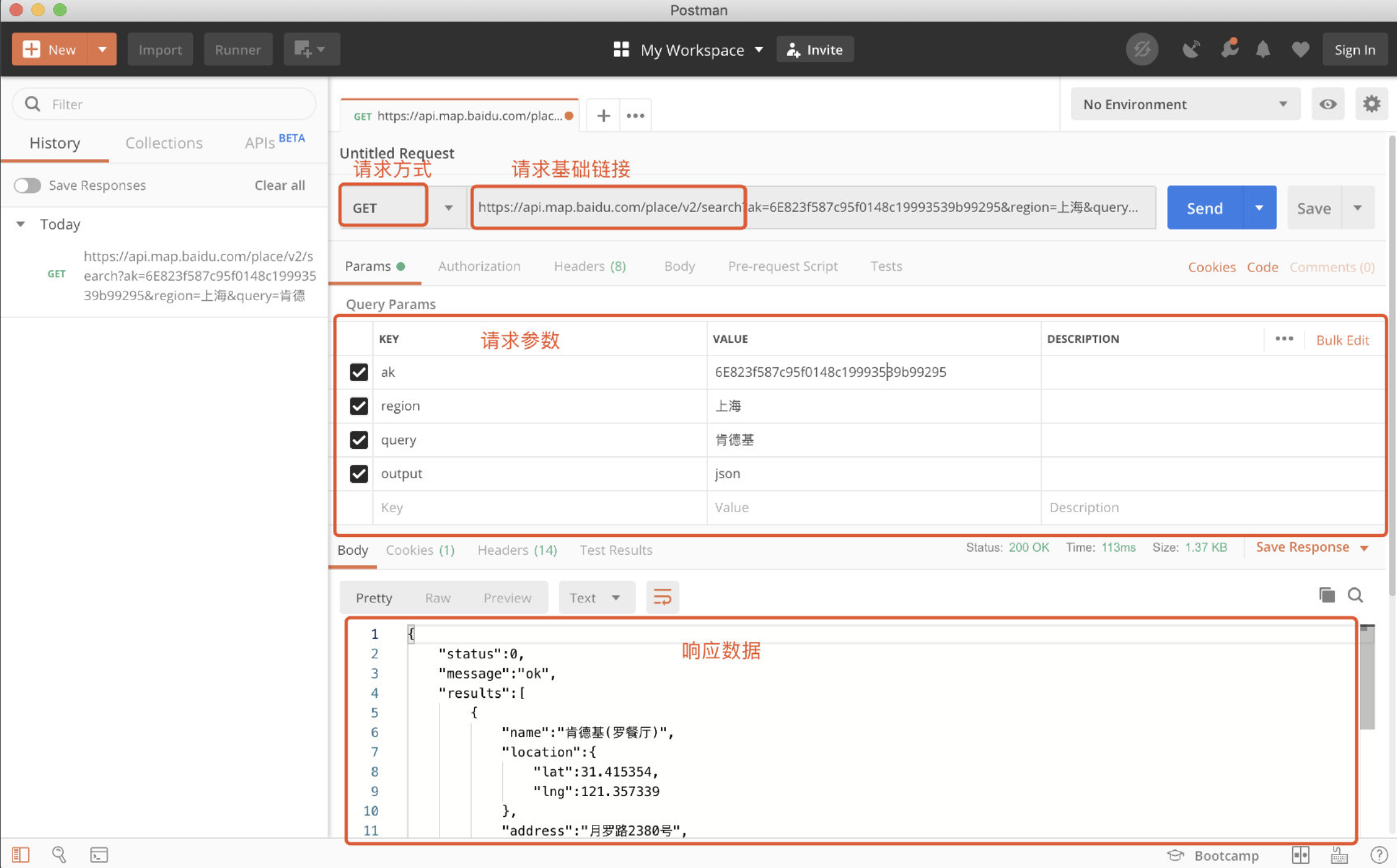
drf入门规范
一 Web应用模式 在开发Web应用中,有两种应用模式: 1.1 前后端不分离 1.2 前后端分离 二 API接口 为了在团队内部形成共识、防止个人习惯差异引起的混乱,我们需要找到一种大家都觉得很好的接口实现规范,而且这种规范能够让后端写…...

【微服务】springboot整合minio详解
目录 一、前言 二、Minio 概述 2.1 Minio简介 2.1 Minio特点 三、Minio 环境搭建 3.1 部署过程 3.1.1 拉取镜像 3.1.2 启动容器 3.1.3 访问web页面 四、Minio基本使用 4.1 基本概念 4.2 上传文件演示 4.3 用户管理 4.4 Java操作Minio 4.4.1 导入依赖 4.4.2 上传…...
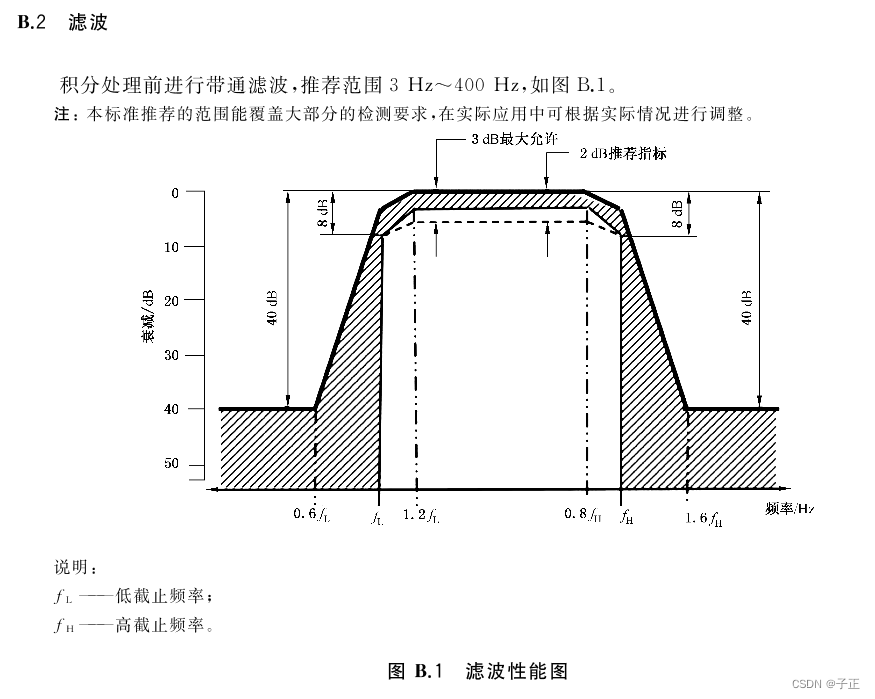
减速机振动相关标准 - 笔记
参考标准:国家标准|GB/T 39523-2020 减速机的振动标准与发动机不同,摘引: 原始加速度传感器波形 可以明显看到调幅波 它的驱动电机是300Hz~2000Hz范围的。这个采样时间是5秒,看分辨率至少1024线。可分出500条谱线。 频谱部分 …...

【matlab】MATLAB 中的标量运算及实例
MATLAB 中的标量运算及实例 引言 在 MATLAB 中,标量是指只包含单个数值的变量或常量。尽管标量运算可能看似简单,但它在数值计算、数据处理和算法设计中扮演着重要的角色。本文将深入探讨 MATLAB 中的标量运算,介绍其基本操作和一些实例应用。 1. 标量运算的基本操作 标…...

java简易制作-王者荣耀游戏
一.准备工作 首先创建一个新的Java项目命名为“王者荣耀”,并在src下创建两个包分别命名为“com.sxt"、”com.stx.beast",在相应的包中创建所需的类。 创建一个名为“img”的文件夹来储存所需的图片素材。 二.代码呈现 package com.sxt; import javax…...

手撕分布式缓存---多节点的调取
经过上一个章节的学习,我们已经知晓了如何搭建了HTTP Server,通过HTTP协议与我们定义的路由,我们可以远程访问这个节点;基于这一点,我们可以部署多台实现了HTTP的缓存服务从而实现分布式的特性。这一章节我们要基于此背…...
C/C++编程中的算法实现技巧与案例分析
C/C编程语言因其高效、灵活和底层的特性,被广大开发者用于实现各种复杂算法。本文将通过10个具体的算法案例,详细探讨C/C在算法实现中的技巧和应用。 一、冒泡排序(Bubble Sort) 冒泡排序(Bubble Sort)是一…...
干货分享 | 如何在TSMaster中对常用总线报文信号进行过滤?
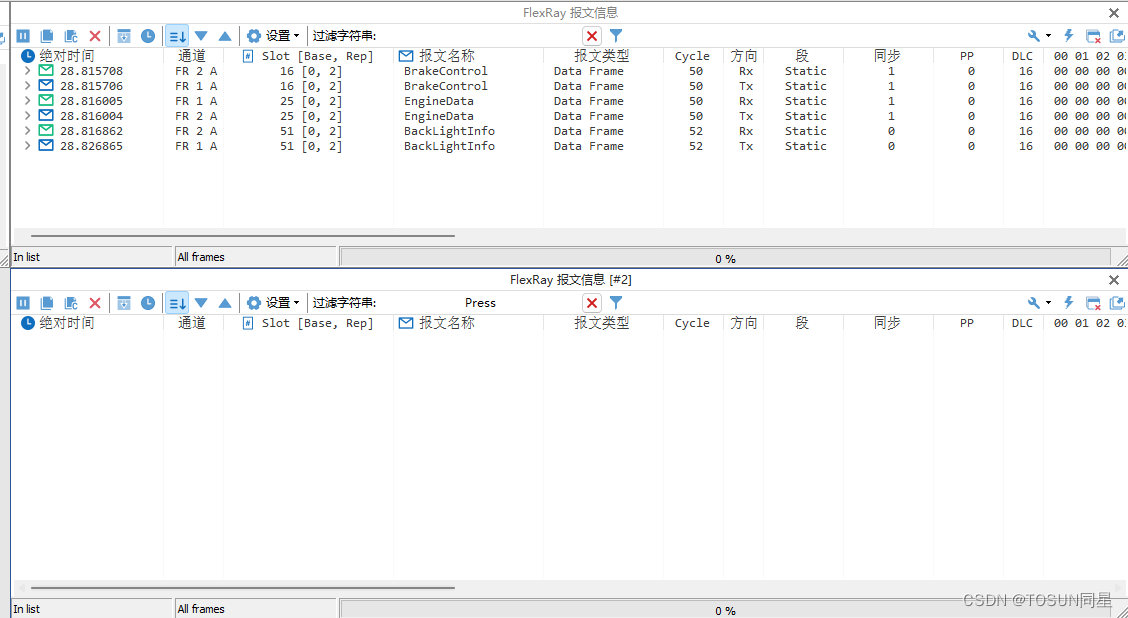
TSMaster软件平台支持对不同总线(CAN、LIN、FlexRay)的报文和信号过滤,过滤方法一般有全局接收过滤、数据流过滤、窗口过滤、字符串过滤、可编程过滤,针对不同的总线信号过滤器的使用方法也基本相同。今天重点和大家分享一下关于T…...
k8s链接数据库故障Waiting for table metadata lock
场景:早上来发现一个程序,链接mysql数据库有点问题,随后排查,因为容器在k8s里面。所以尝试重启了pod没有效果 一、重启pod: 这里是几种在Kubernetes中重启Pod的方法: 删除Pod,利用Deployment重建 kubectl delete pod mypodDepl…...

数字经济如何驱动企业高质量发展? ——核心机制、模式选择与推进路径
文章目录 每日一句正能量前言核心机制信息化和智能化作为数字经济的核心机制信息化和智能化如何提升企业生产效率和管理水平数据的获取、分析和利用对企业发展的影响 模式选择电子商务模式的选择共享经济模式的选择数据驱动的业务模式选择 推进路径建设数字化基础设施培养数字化…...
机器学习——支持向量机
目录 一、基于最大间隔分隔数据 二、寻找最大间隔 1. 最大间隔 2. 拉格朗日乘子法 3. 对偶问题 三、SMO高效优化算法 四、软间隔 五、SMO算法实现 1. 简化版SMO算法 2. 完整版SMO算法 3. 可视化决策结果 六、核函数 1. 线性不可分——高维可分 2. 核函数 …...

mq的作用
使用mq优点 mq是一种常见的中间件,在项目中经常用到,它具有异步、解耦、削峰填谷的作用。 异步 比如下单流程,A服务—>B服务,总的耗时是A耗时时间B耗时时间,而改为A—>mq---->B后,A发送mq后立刻…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...
