深度学习中的高斯分布
1 高斯分布数学表达
1.1 什么是高斯分布
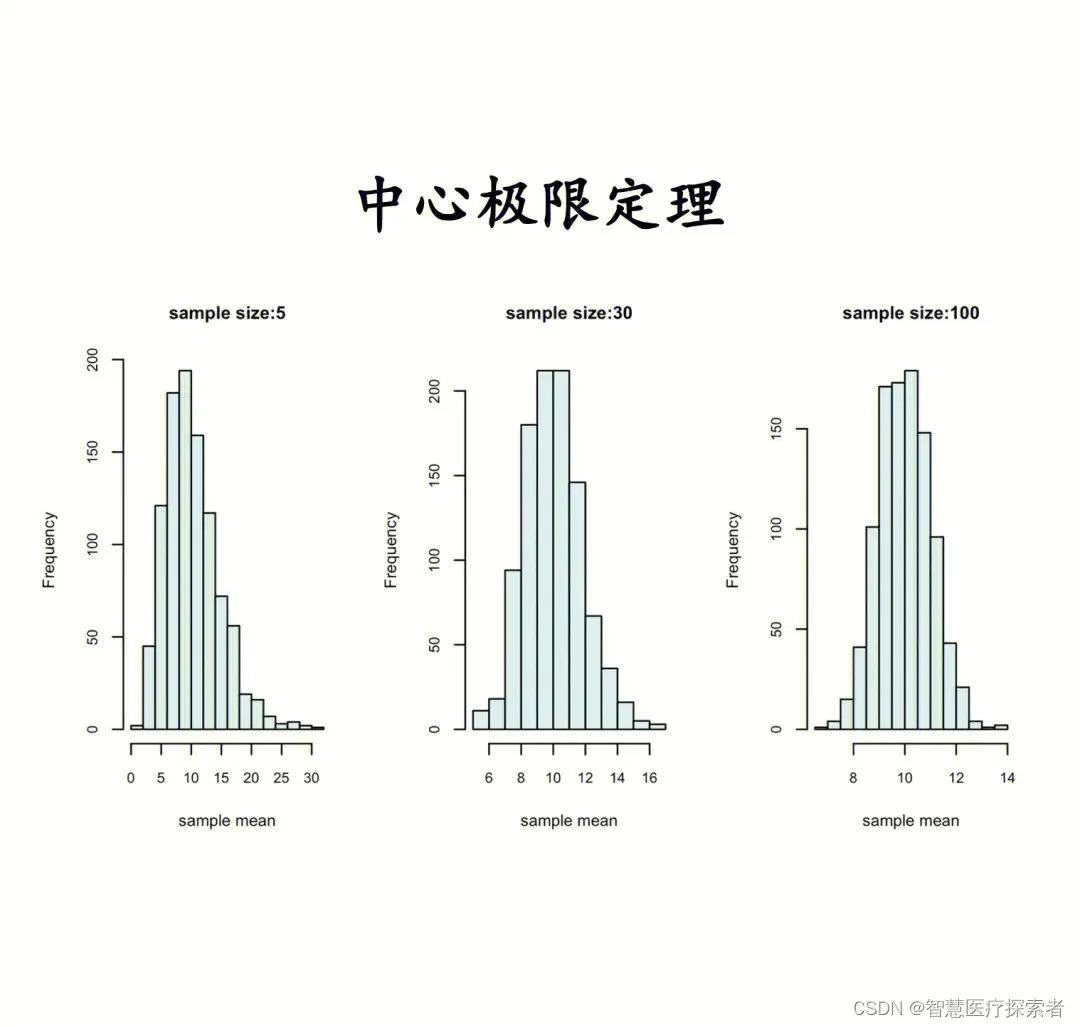
高斯分布(Gaussian Distribution)又称正态分布(Normal Distribution)。高斯分布是一种重要的模型,其广泛应用于连续型随机变量的分布中,在数据分析领域中高斯分布占有重要地位。由于中心极限定理(Central Limit Theorem)的广泛应用,高斯分布在统计学上非常重要。中心极限定理表明,由一组独立同分布,并且具有有限的数学期望和方差的随机变量X1,X2,X3,...Xn构成的平均随机变量Y近似的服从正态分布当n趋近于无穷。另外众多物理计量是由许多独立随机过程的和构成,因而往往也具有高斯分布。
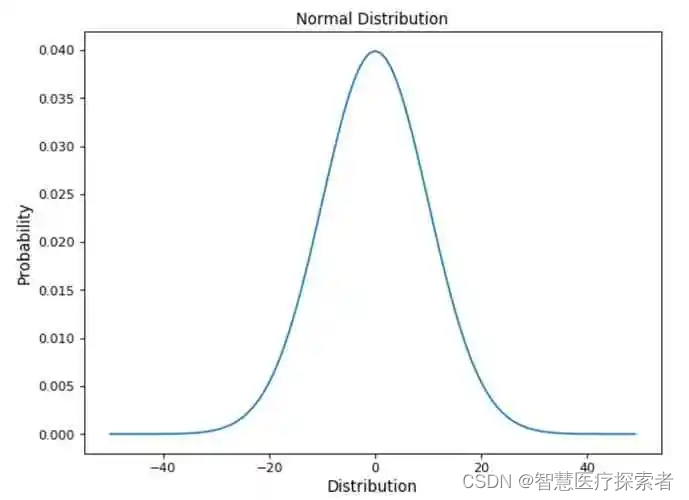
高斯分布的概率密度函数曲线呈钟形,因此又经常称之为钟形曲线。即随机变量X服从一个为数学期望μ、方差为σ^2的高斯分布,记为N(μ,σ^2)。在高斯分布中,以数学期望μ表示钟型的中心位置(也即曲线的位置),而标准差(standard deviation)σ表征曲线的离散程度。
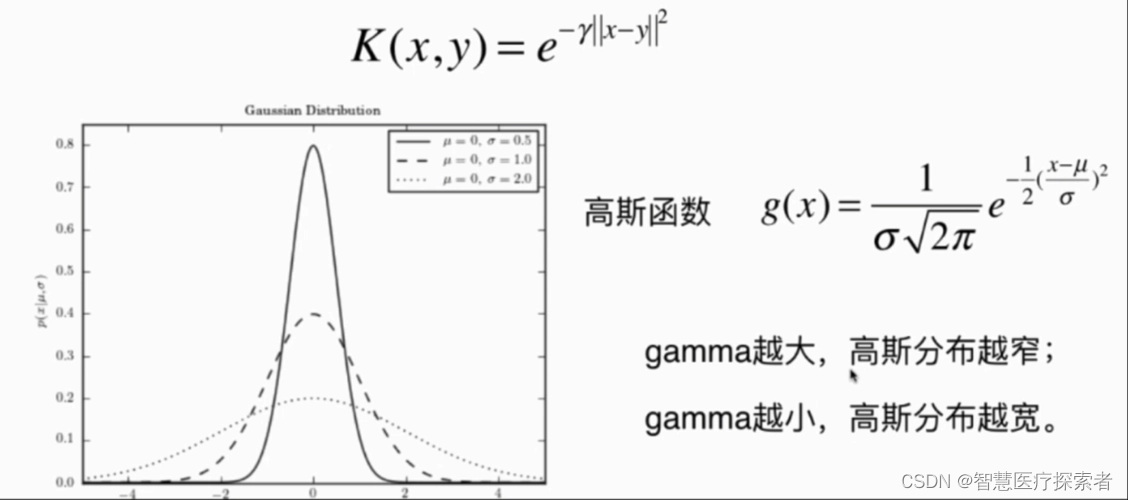
当数学期望为0(u=0),方差为1(σ=1)时,该分布为标准正态分布(standard normal distribution)。下图展示了几种不同类型的正态分布概率密度函数曲线。
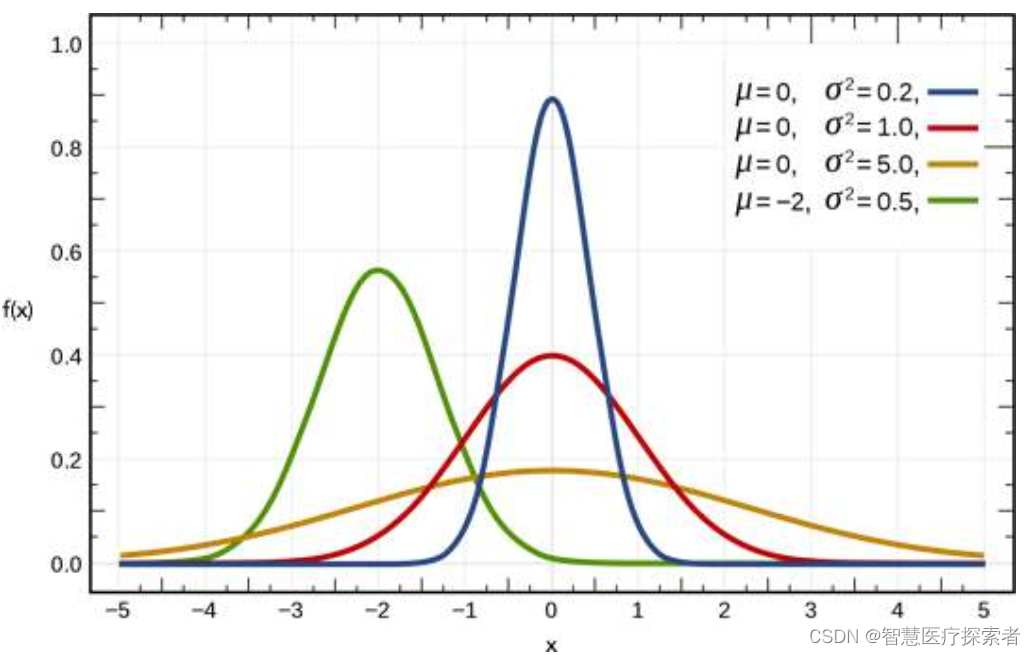
1.2 关键概念
-
概率函数:把事件概率表示成关于事件变量的函数
-
概率分布函数:一个随机变量ξ取值小于某一数值x的概率,这概率是x的函数,称这种函数为随机变量ξ的分布函数,简称分布函数,记作F(x),即F(x)=P(ξ<x) (-∞<x<+∞),由它并可以决定随机变量落入任何范围内的概率。
-
概率密度函数:
概率密度等于变量在一个区间(事件的取值范围)的总的概率除以该段区间的长度。
概率密度函数是一个描述随机变量在某个确定的取值点附近的可能性的函数。
1.3 一元高斯分布
若随机变量X服从均值为μ,方差为σ2的高斯分布,那么:

高斯分布的图形像钟一样,下图展示了一般正态分布的图形。其中 μ = 0 , σ = 1。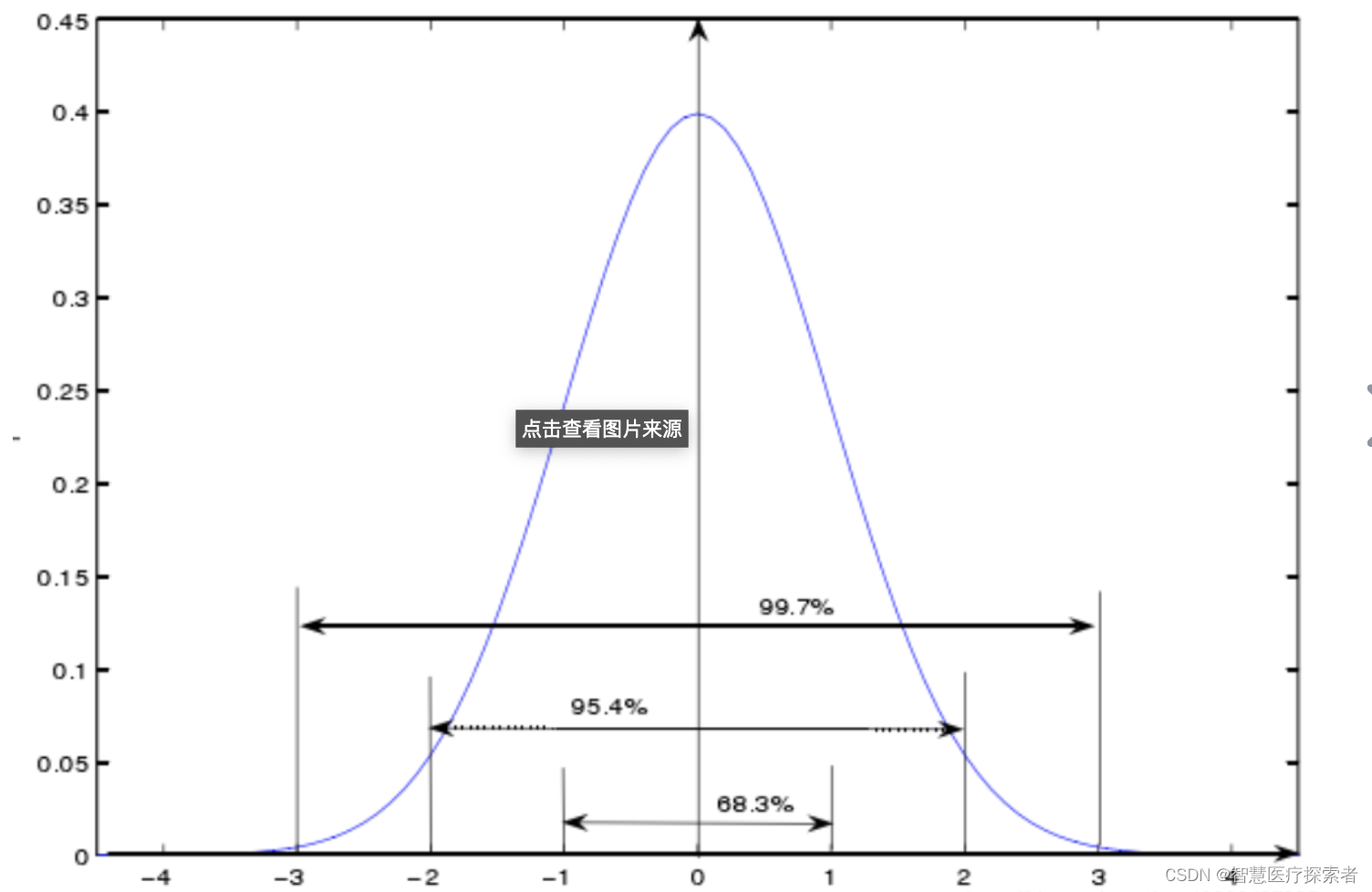
对于一个非标准的正态分布,可以由标准正态分布经过以下3步变换得到:
-
将x向右移动u个单位
-
将密度函数x轴延展sigma倍
-
将函数密度图像y轴压缩σ倍
如果X服从分布,X ∼ N(μ, σ2),那么具有以下的性质:

1.4 多元高斯分布
1.4.1 独立多元高斯分布

如果我们令:
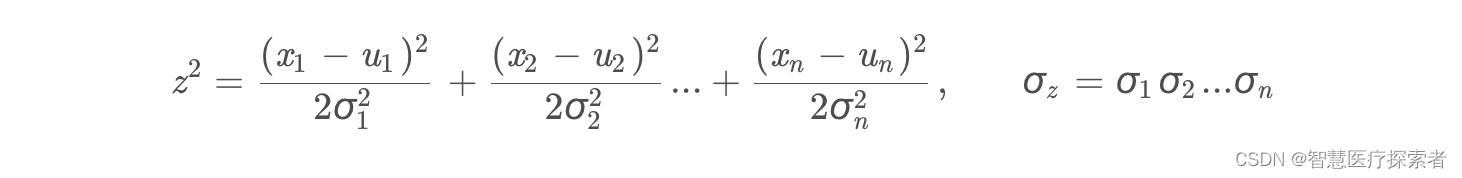
我们有:
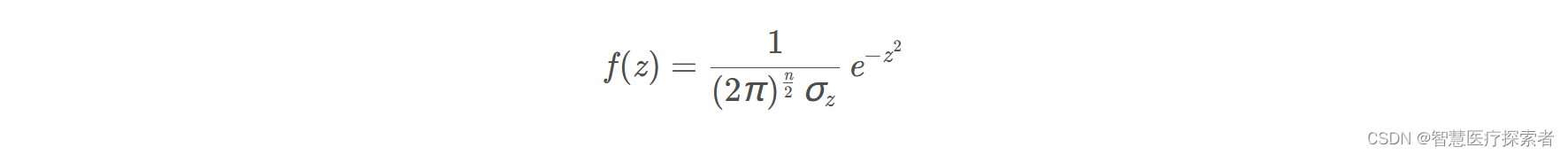
使用矩阵的形式来表示的话,则有:
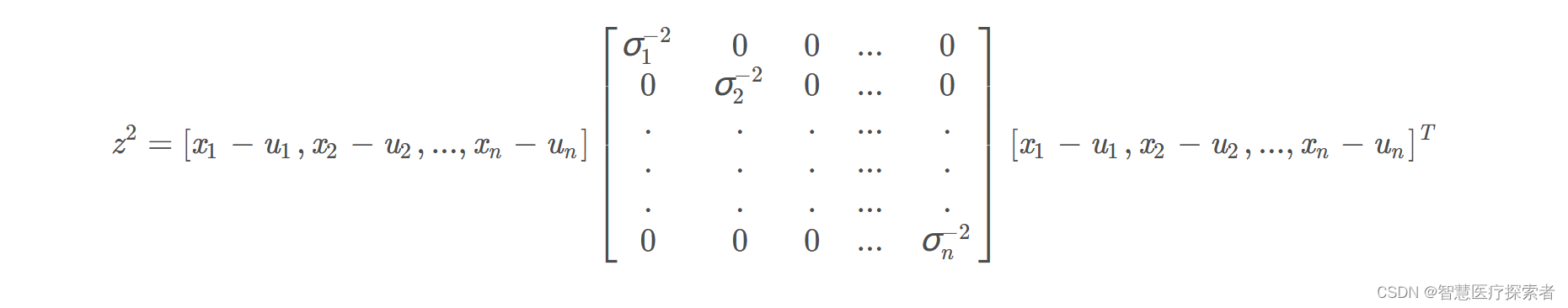
定义符号:
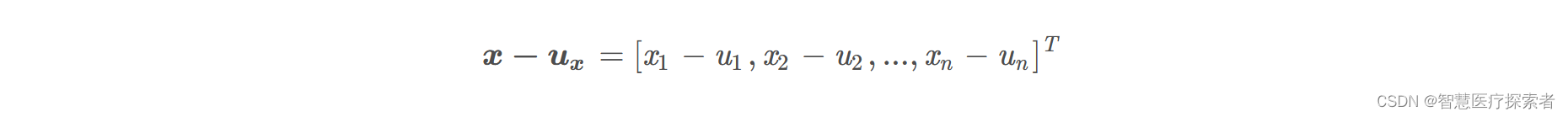
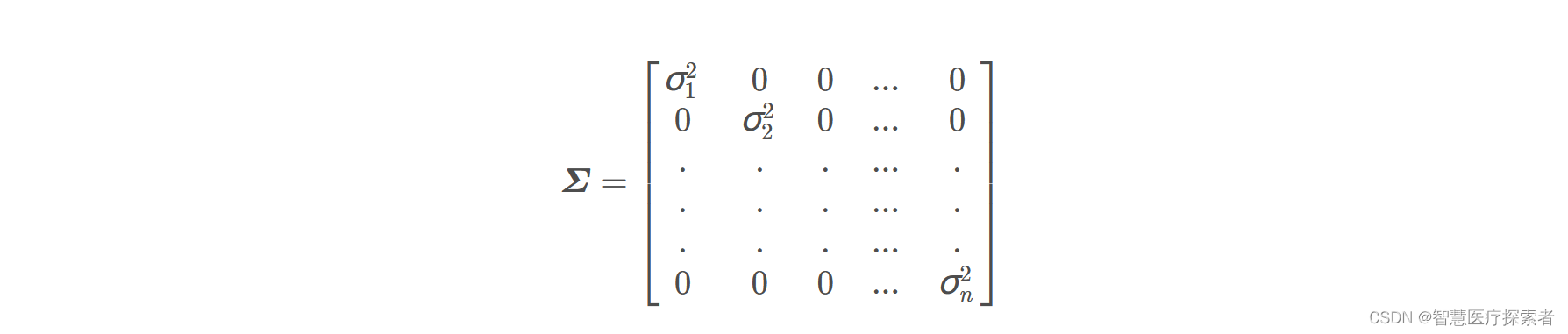
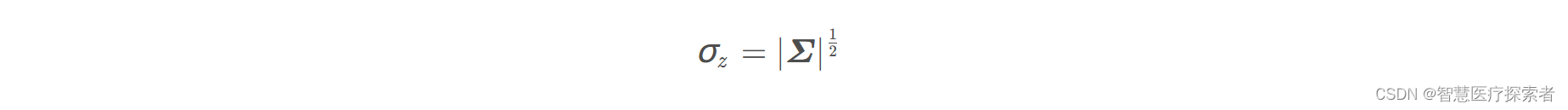
变量代换可得:
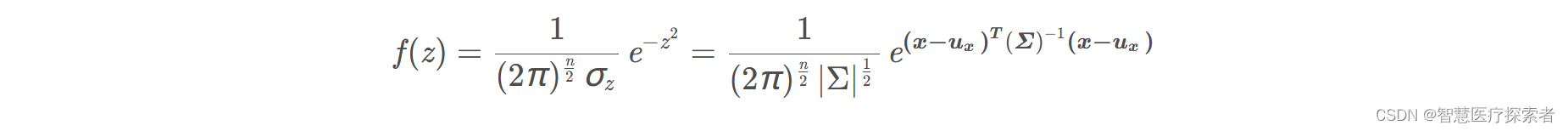
下面以 为例,画出二元高斯分布在变量之间相互独立的图像:

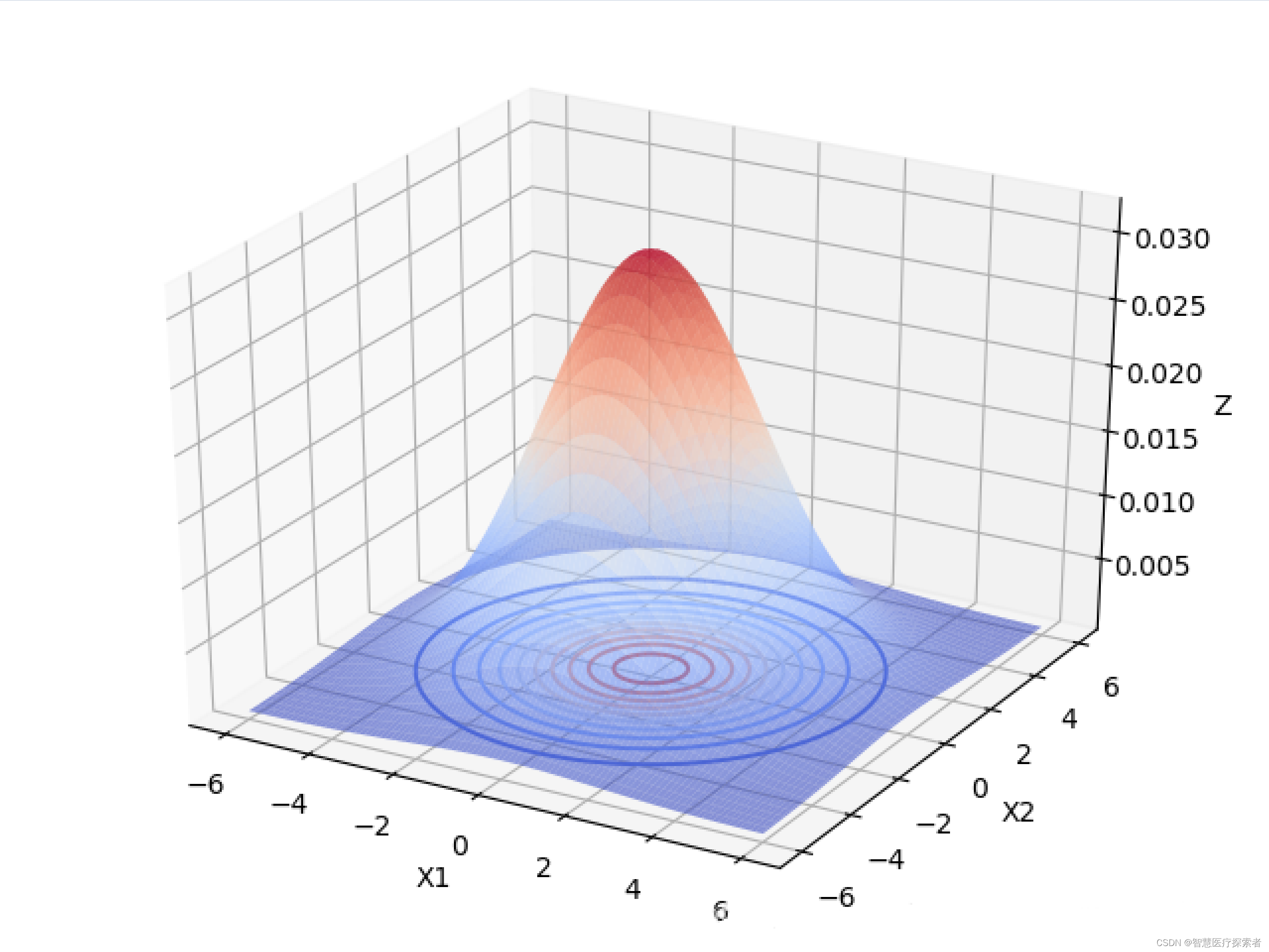

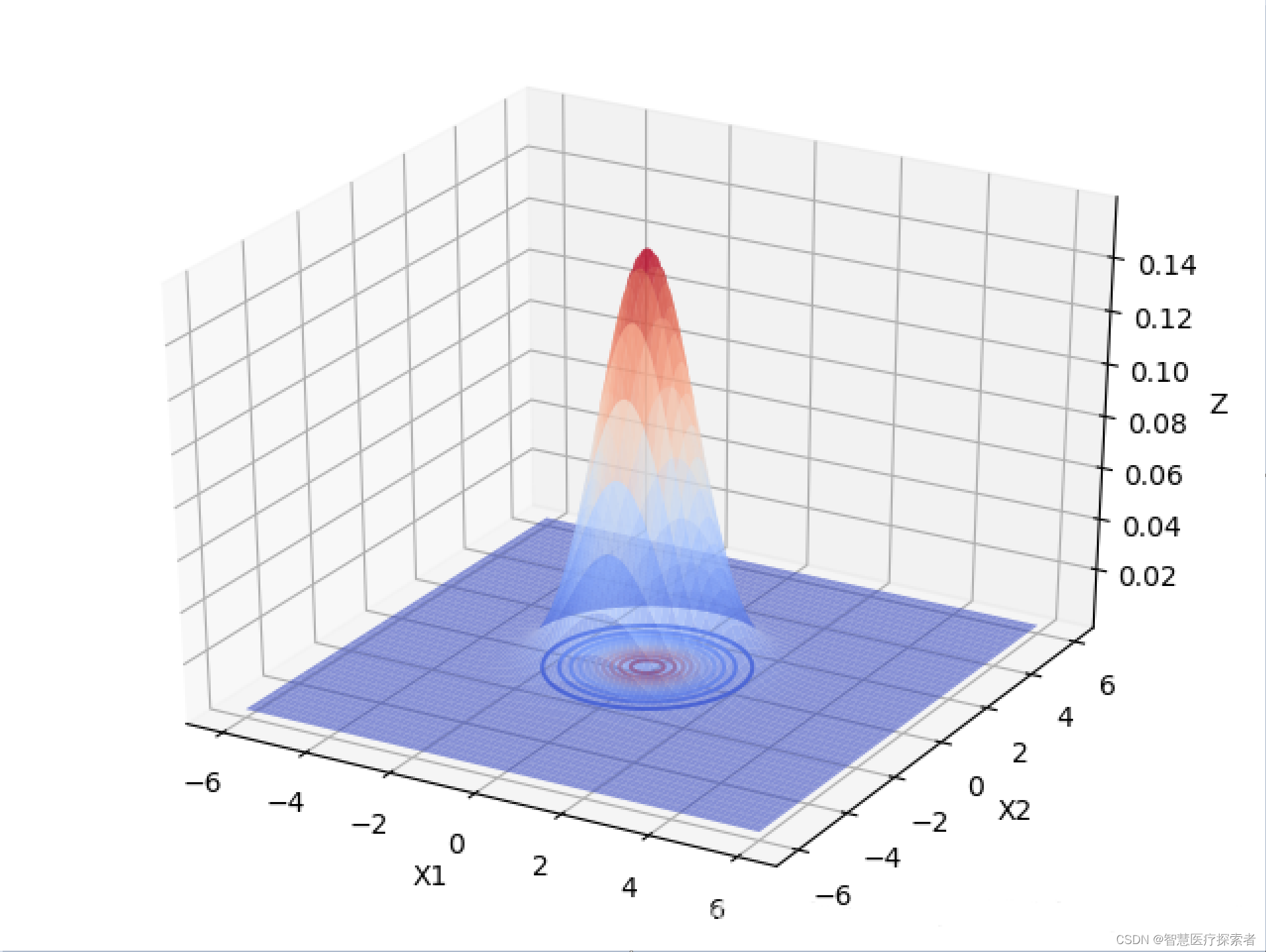

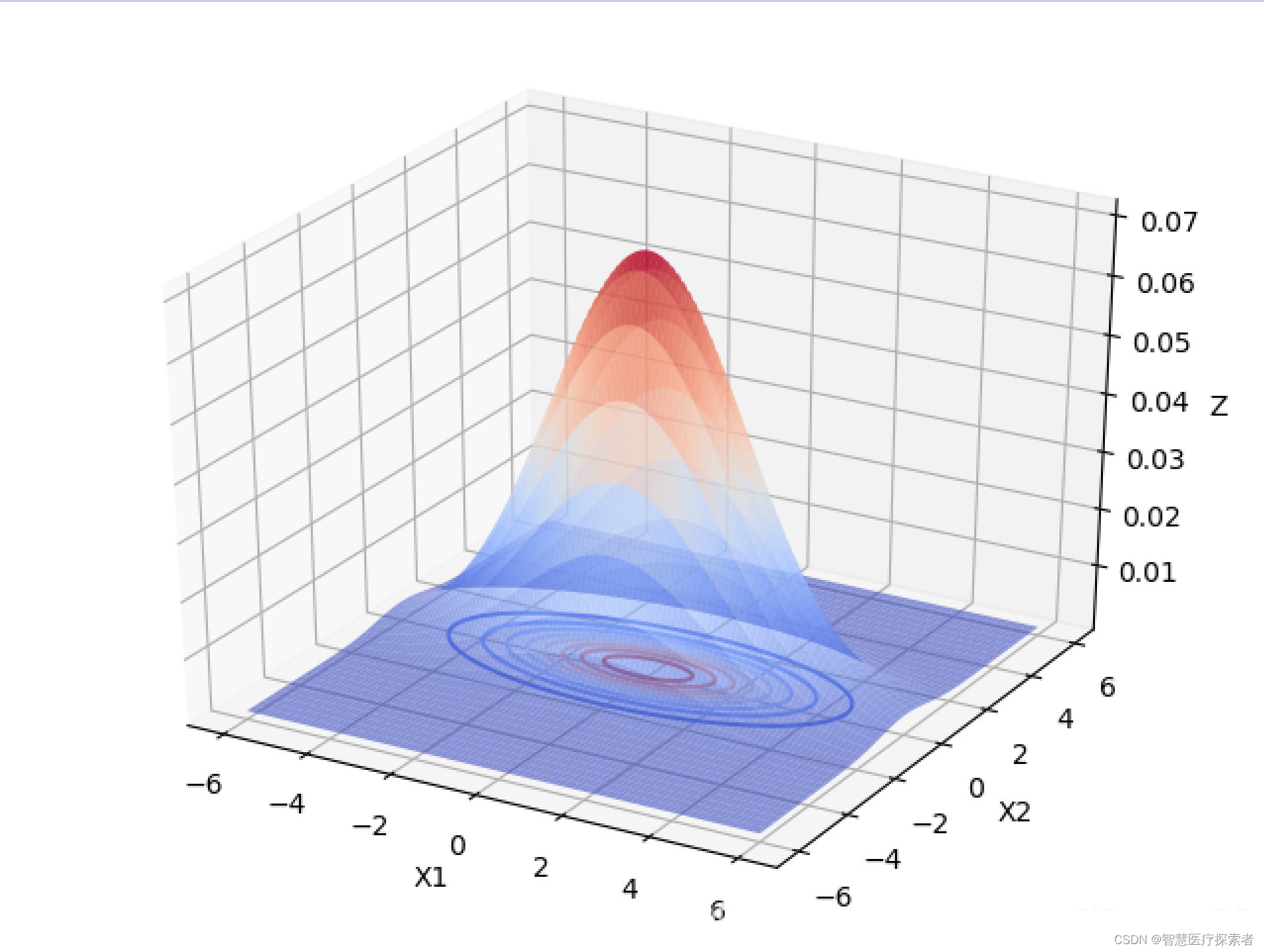

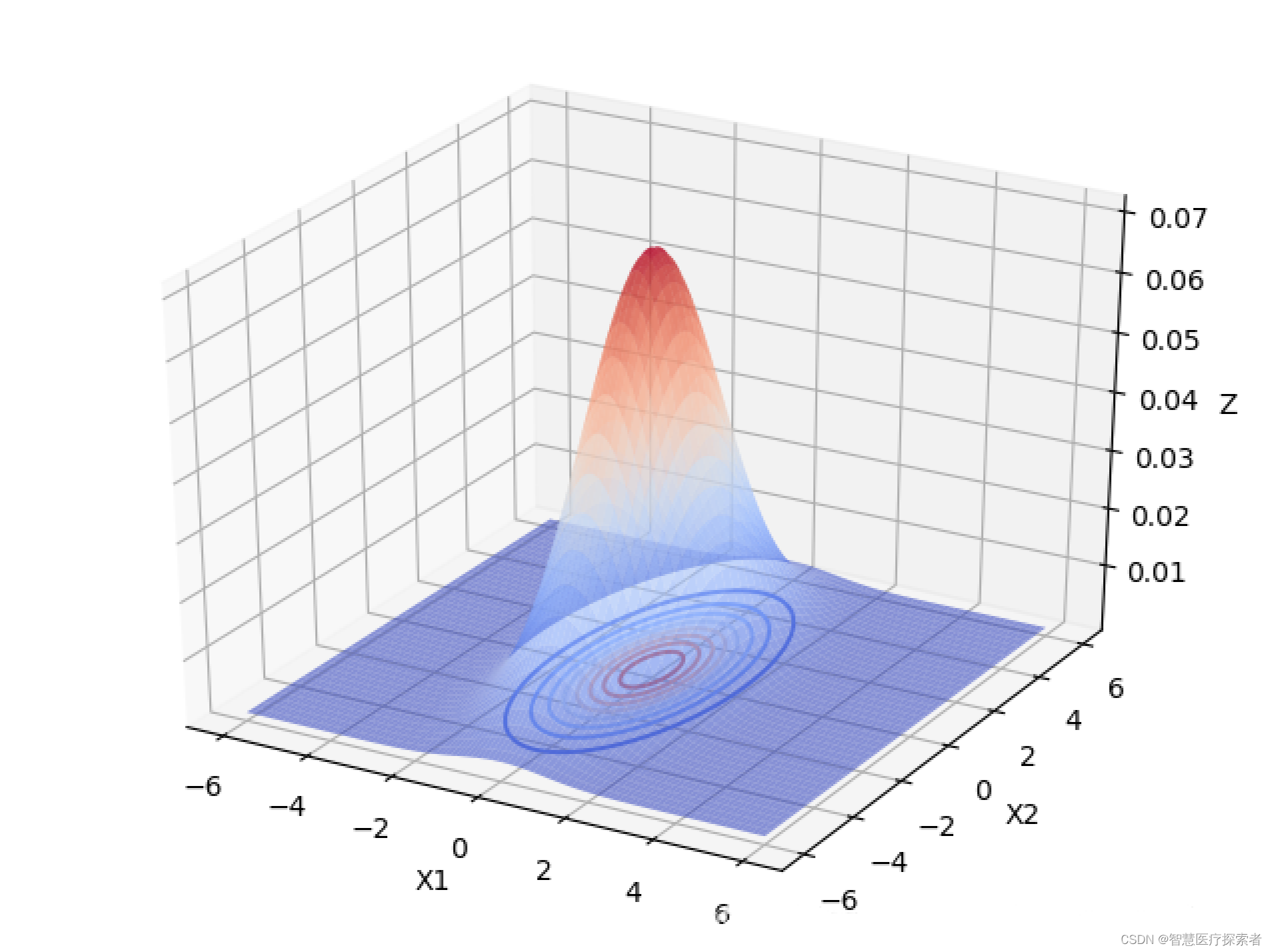
由上图可以看出,当变量之间相互独立的时候:
-
当协方差矩阵的特征值越小时,分布函数图像越高越尖。
-
当协方差矩阵的特征值相等时,分布函数图像在X1,X2面上的投影是圆形的。当特征值不相等时,分布函数图像在X1,X2面上的投影是椭圆形的,X1,X2相互独立时,椭圆的长轴和短轴平行与坐标轴。且变量对应的特征值越大,该变量分布的范围越分散,在二元高斯分布中,对应特征值大的变量在函数投影图像中对应的是椭圆的长轴。高维的高斯分布情况可以按照这个规律进行推广。
1.4.2 多元相关变量高斯分布
当变量之间存在相关关系的时候,协方差矩阵不再是对角阵,而是一个对称的矩阵,矩阵的每个元素表示变量
的协方差。

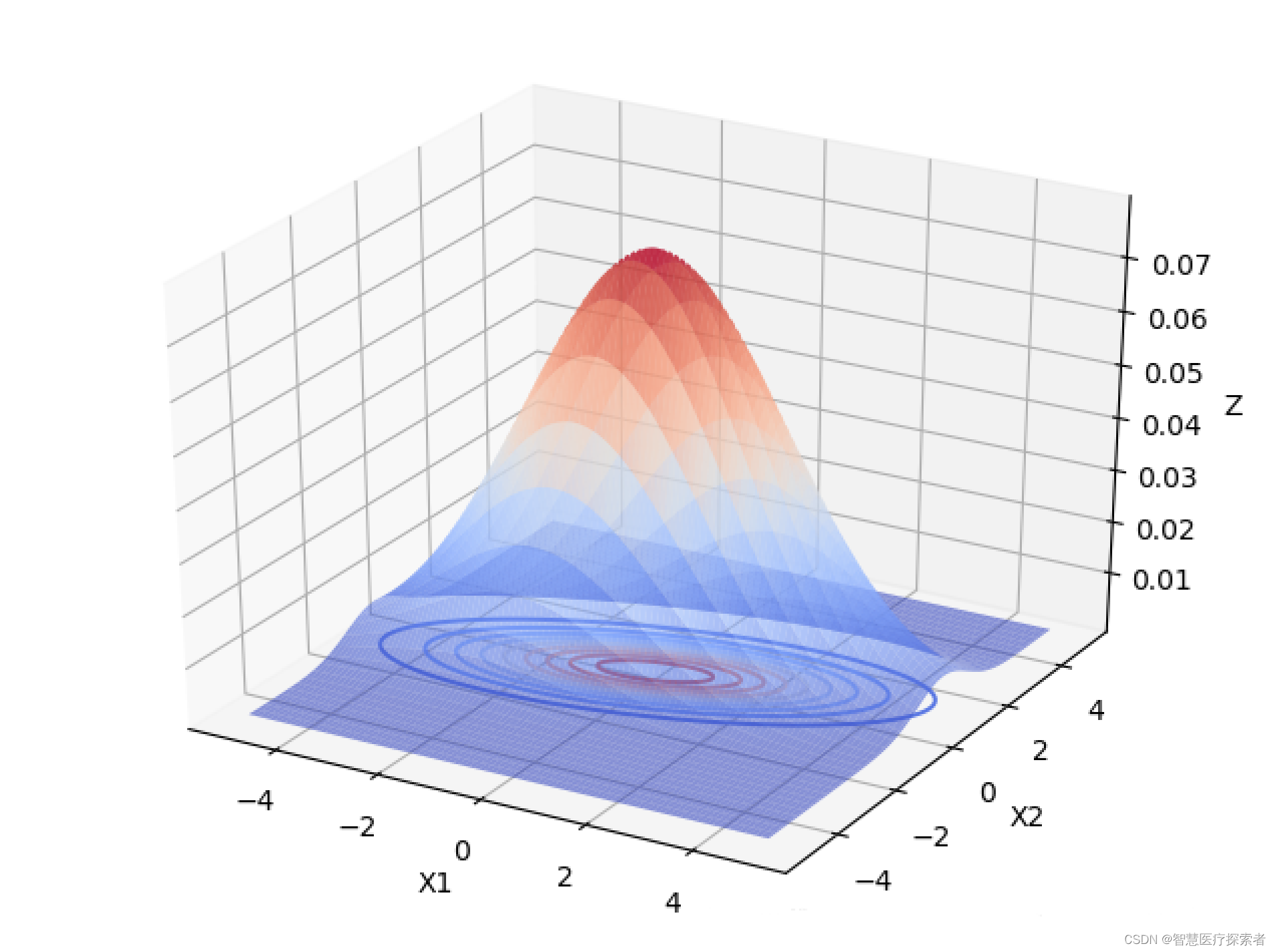

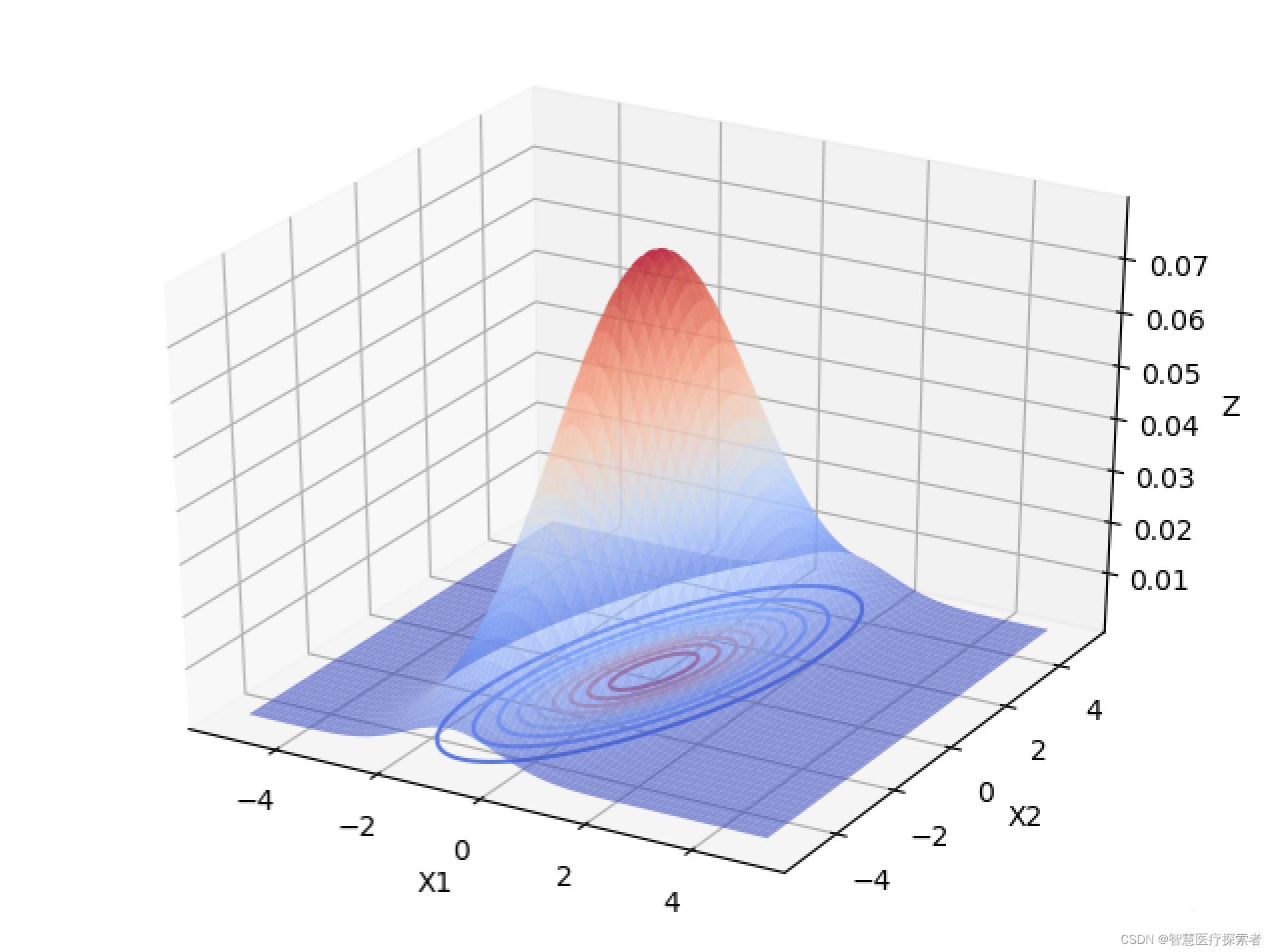
从上面2个图像中可以看出,变量之间具有相关关系时,与变量之间相互独立最大的区别是,投影面的椭圆长短轴不再平行与坐标轴。如果我们将坐标轴X1,X2旋转一下,与椭圆的长短轴平行,如下图所示:
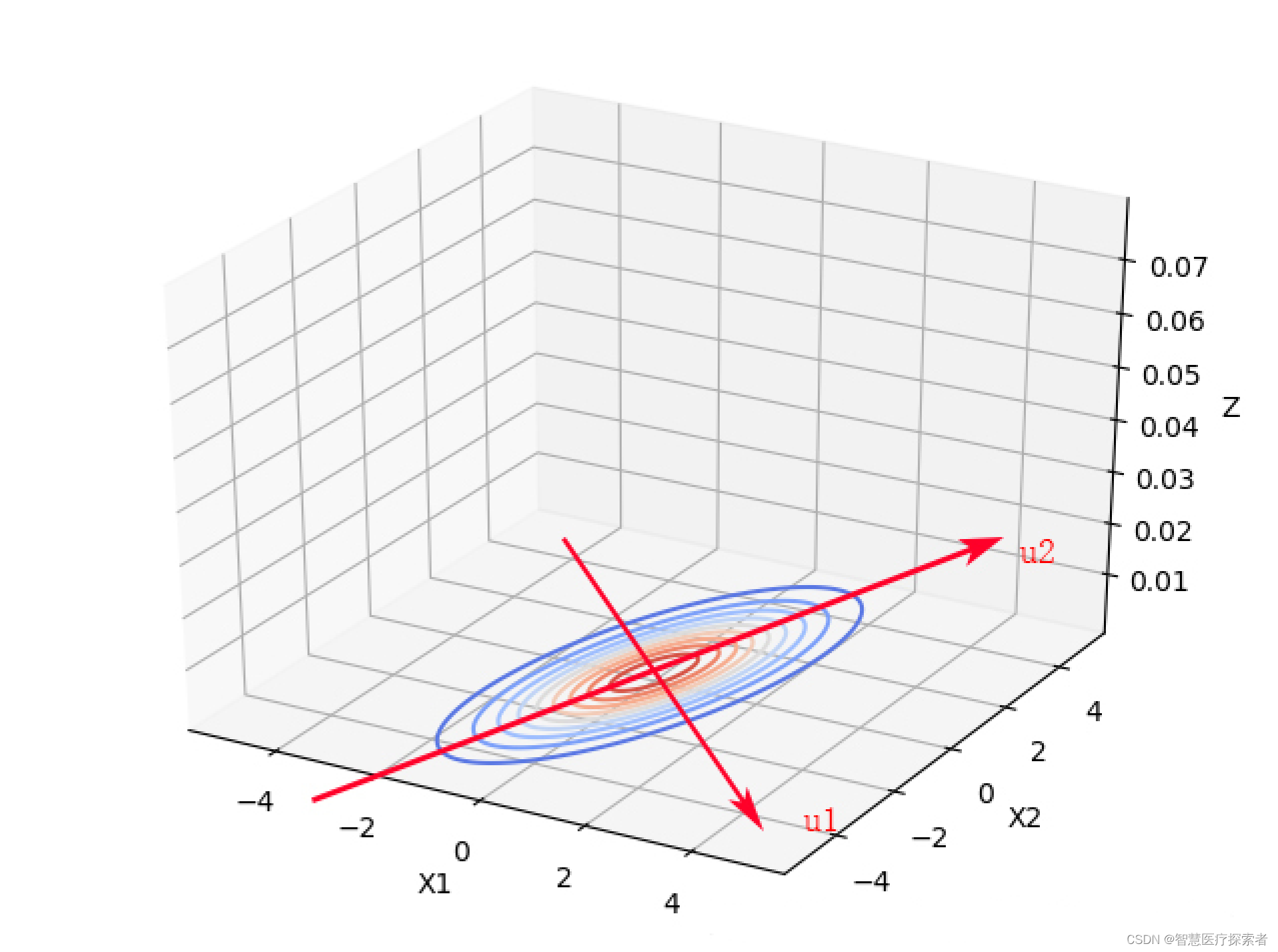
由独立变量的二元高斯分布知,那么在新的坐标系下, 是相互独立的。上述过程称作为去相关性,这也是经典的降维方法主成分分析PCA的基础。以下是新坐标系的求解和原坐标系上的点在新坐标系下的坐标数学表达。
根据协方差矩阵的特征方程求解协方差矩阵的单位正交特征向量(先求出特征向量,再进行正交化与单位化),


此时之间没有相关关系。
2 高斯分布在深度学习中的作用
2.1 高斯分布广泛使用的原因
高斯分布(也称为正态分布或钟形曲线)在深度学习中被广泛应用的原因有以下几个方面:
-
中心极限定理:高斯分布具有重要的数学性质,其中最重要的是中心极限定理。该定理指出,对于大多数随机变量的和,其分布趋向于高斯分布。这意味着在实际问题中,许多现象可以通过高斯分布来近似描述。
-
参数化灵活性:高斯分布具有两个重要参数,均值和标准差,可以通过这两个参数来灵活地调整分布的形状。这使得高斯分布能够适应不同数据集的特征,并具有较强的拟合能力。
-
中心性和离散性度量:高斯分布在数学上具有对称性,其均值和中位数相等,这使得它成为测量数据集中心性的一种常用方法。此外,标准差作为高斯分布的度量,能够衡量数据的离散程度。
-
最大似然估计:在概率统计中,最大似然估计是一种常用的参数估计方法。高斯分布的参数估计可以通过最大似然估计进行计算,这使得高斯分布的应用更为方便。
在实际意义上,高斯分布在自然界和社会现象中出现的频率很高。许多自然和社会现象具有随机性,并且可以用高斯分布来描述。例如,在测量误差、人口统计、金融市场波动等领域中,高斯分布都被广泛应用。
2.2 高斯分布的应用场景
高斯分布(也称为正态分布)在深度学习模型中扮演着多个重要角色。以下是一些主要的应用场景:
-
参数初始化:在神经网络的训练开始时,通常需要对权重进行初始化。使用高斯分布(尤其是标准正态分布)来初始化权重可以帮助在训练初期避免激活函数的饱和,确保初始权重既不太大也不太小。
-
正则化:在某些情况下,高斯分布被用作先验分布,加入到损失函数中作为正则化项。这种正则化(如 L2 正则化)可以帮助防止过拟合,通过对权重的大小进行约束。
-
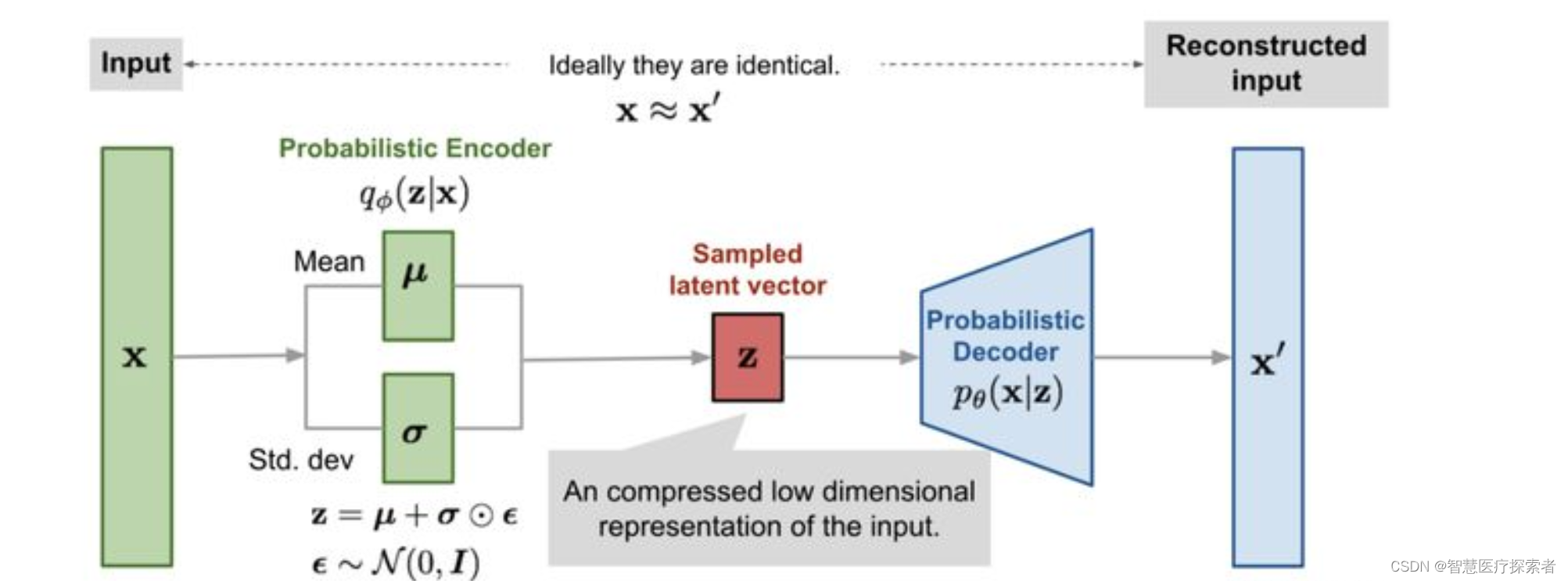
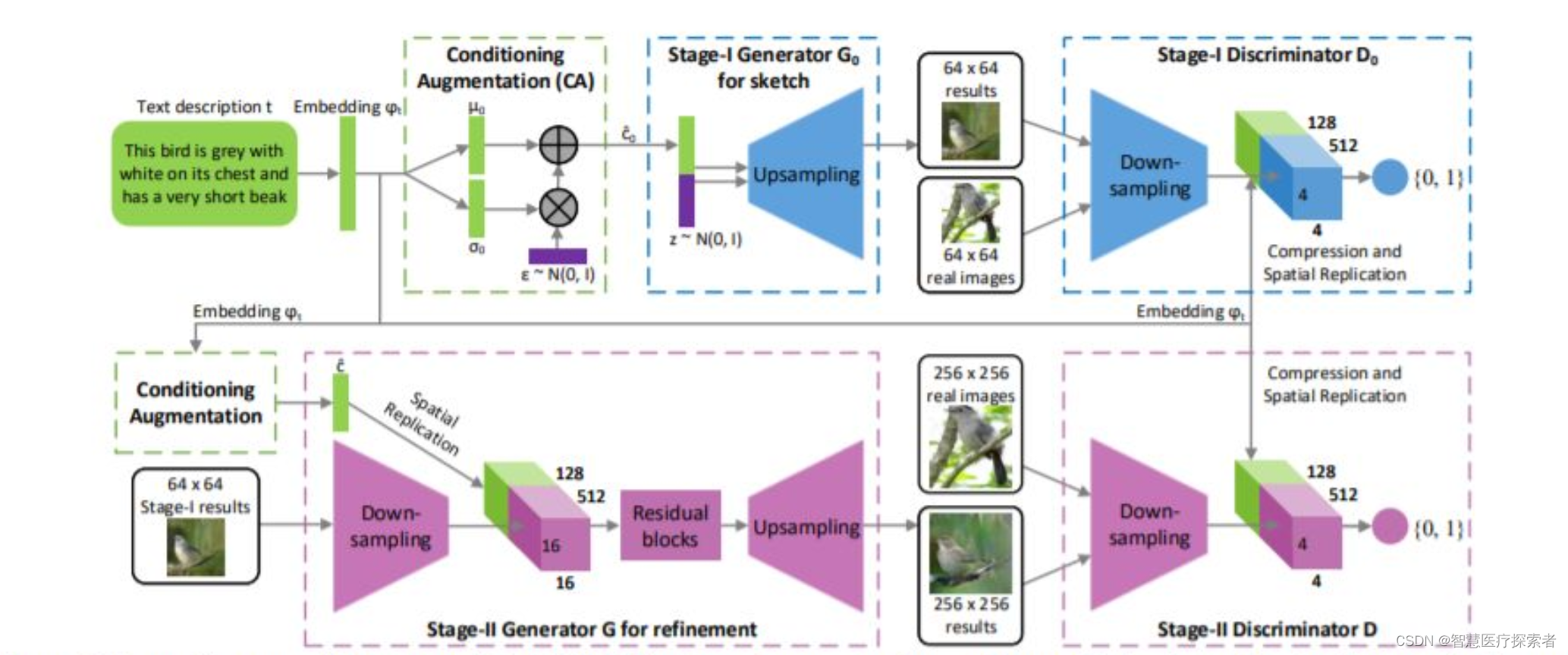
生成模型:在生成对抗网络(GANs)和变分自编码器(VAEs)等生成模型中,高斯分布常用于生成潜在空间中的随机噪声。这些噪声向量后续被用来生成数据(如图像)。
-
概率建模:在许多概率深度学习模型中,高斯分布用于建模输出变量,尤其是在处理连续值(如回归问题)时。
-
激活函数:尽管不太常见,但在某些特殊的网络结构中,可以使用高斯函数作为激活函数,以模拟特定的生物神经网络行为。
-
不确定性估计:在贝叶斯神经网络中,权重和偏置被视为随机变量,通常使用高斯分布来描述它们的不确定性。这种方法可以提供模型预测的不确定性估计。
-
特征提取:在某些图像处理技术中,例如高斯模糊,使用高斯分布作为权重核,可以帮助模型在训练过程中更好地提取图像特征。
高斯分布由于其数学属性和在自然界中的普遍性,成为深度学习中的一个重要工具。它在处理不确定性、正则化和概率建模方面尤为重要。
相关文章:

深度学习中的高斯分布
1 高斯分布数学表达 1.1 什么是高斯分布 高斯分布(Gaussian Distribution)又称正态分布(Normal Distribution)。高斯分布是一种重要的模型,其广泛应用于连续型随机变量的分布中,在数据分析领域中高斯分布占有重要地位。由于中心极限定理(Central Limit…...

【已解决】Atlas 导入 Hive 元数据,执行 import-hive.sh 报错
部署完 Atlas 之后,尝试导入 Hive 元数据,遇到了一些错误,特此记录一下,方便你我他。 执行 import-hive.sh 报错 [omchadoop102 apache-atlas-2.2.0]$ hook-bin/import-hive.sh Using Hive configuration directory [/opt/module…...

在 Windows PC 上轻松下载并安装 FFmpeg
FFmpeg 是一种开源媒体工具,可用于将任何视频格式转换为您需要的格式。该工具只是命令行,因此它没有图形、可点击的界面。如果您习惯使用常规图形 Windows 程序,安装 FFmpeg 一开始可能看起来很复杂,但不用担心,它;很简…...

21.Servlet 技术
JavaWeb应用的概念 在Sun的Java Servlet规范中,对Java Web应用作了这样定义:“Java Web应用由一组Servlet、HTML页、类、以及其它可以被绑定的资源构成。它可以在各种供应商提供的实现Servlet规范的 Servlet容器 中运行。” Java Web应用中可以包含如下…...

【Hive】——DDL(PARTITION)
1 增加分区 1.1 添加一个分区 ALTER TABLE t_user_province ADD PARTITION (provinceBJ) location/user/hive/warehouse/test.db/t_user_province/provinceBJ;必须自己把数据加载到增加的分区中 hive不会帮你添加 1.2 一次添加多个分区 ALTER TABLE table_name ADD PARTITION…...

SpringBoot 源码解析4:事件监听器
SpringBoot 源码解析4:事件监听器 1. 初始化监听器2. 创建事件发布器 SpringApplicationRunListeners3. 事件分发流程3.1 SimpleApplicationEventMulticaster#multicastEvent3.2 获取监听器 AbstractApplicationEventMulticaster#getApplicationListeners3.3 Abstra…...

使用 FastAPI 和 Vue.js 实现前后端分离
简介 前后端分离是现代 Web 开发的趋势。使用 FastAPI 和 Vue.js 可以构建一个高效、灵活且易于维护的 Web 应用。FastAPI 提供了高性能的后端服务,而 Vue.js 作为一种渐进式 JavaScript 框架,可以构建动态的前端界面。本文将详细介绍如何使用 FastAPI …...

算法基础之SPFA判断负环
SPFA判断负环 核心思想:spfa算法 当遍历一个点时 cnt数组记录边数 若有负环 边数会无限1 cnt>n是即为有负环 #include<iostream>#include<cstring>#include<algorithm>#include<queue>using namespace std;const int N 2010 , M 10010…...
)
一些常用的Linux命令及其简要说明(持续更新)
1. cd:改变当前工作目录。 cd [directory]#例如 cd /home/user 2. ls:列出目录内容。 ls [-options] [file/directory]#例如 ls -l, ls /etc 3. pwd:显示当前工作目录。 pwd 4. mkdir:创建新目录。 mkdir [directory]#例…...
开发企业展示小程序的关键步骤和技巧
随着移动互联网的快速发展,小程序已经成为企业展示形象、推广产品和服务的重要工具。拥有一个优秀的小程序可以帮助企业提高品牌知名度,吸引更多潜在客户,提升用户体验。以下是拥有一个展示小程序的步骤: 确定需求和目标 首先&am…...
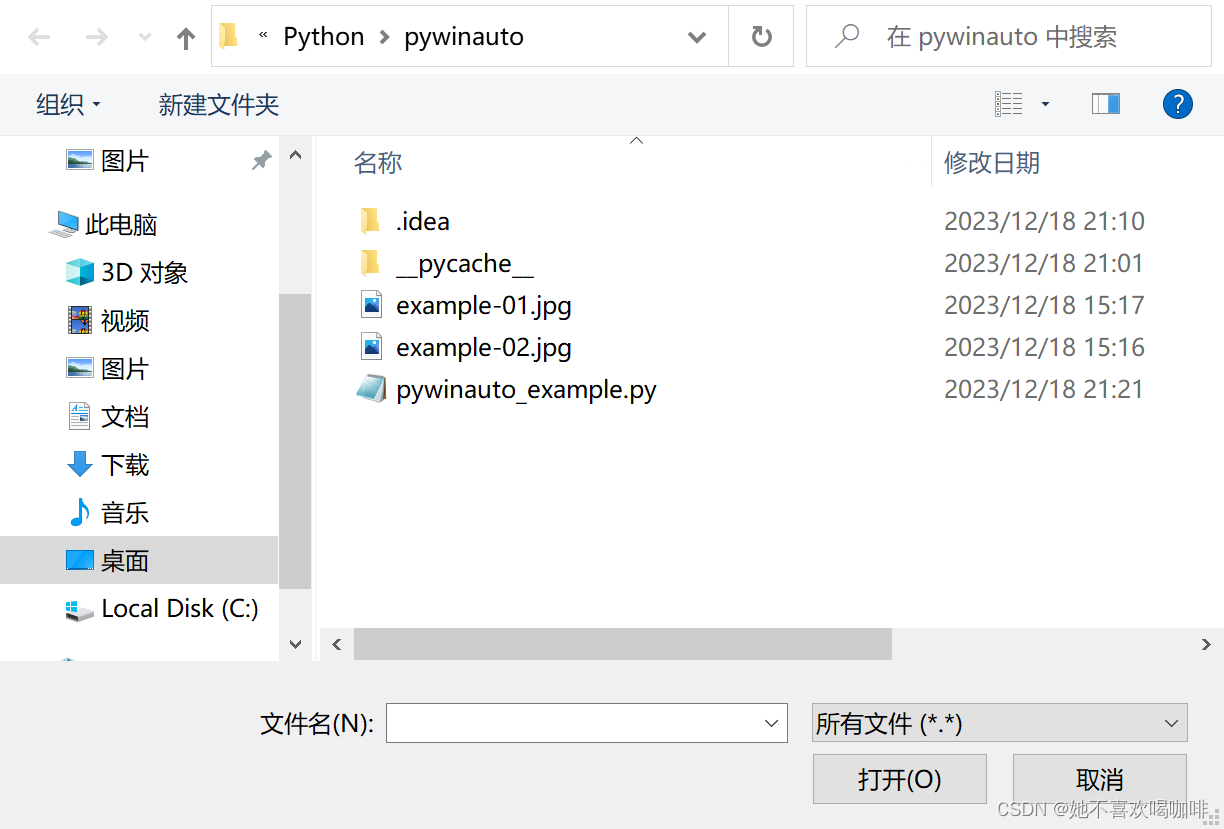
Python-Selenium-使用 pywinauto 实现 Input 上传文件
当前环境:Win10 Python3.7 pywinauto0.6.8,selenium3.14.1 示例代码 from pywinauto import Desktop import osapp Desktop() dialog app[打开] dialog[Edit].set_edit_text(os.getcwd() .\\example-01.jpg) dialog[Button].click() 其他方法&…...

Go语言运行时与自家平台对比后认识
引子 以前就了解Go语言,因为其天生为并发、并行而生,且在语言层面就进行了内秉设计。 总想对比于我们自研的分布式并发、并行平台,以利于得到一些新认识 :) Go官网资料 在Go的官网资料提供了很好的资料和知识库 初…...

leetcode 450. 删除二叉搜索树中的节点
leetcode 450. 删除二叉搜索树中的节点 题目 给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。 一般来说&#x…...
小红书可观测 Metrics 架构演进,如何实现数十倍性能提升?
在当前云原生时代,随着微服务架构的广泛应用,云原生可观测性概念被广泛讨论。可观测技术建设,将有助于跟踪、了解和诊断生产环境问题,辅助开发和运维人员快速发现、定位和解决问题,支撑风险追溯、经验沉淀、故障预警&a…...

selenium学习
前期准备 pip install selenium 获取浏览器驱动 我使用的浏览器是Chrome,所以这里只介绍关于Chrome获取浏览器驱动的方法: 需要注意的是:selenium 4.x 对之前版本的部分API调用方式进行了调整,这里就包括关于浏览器获取驱动的方式…...
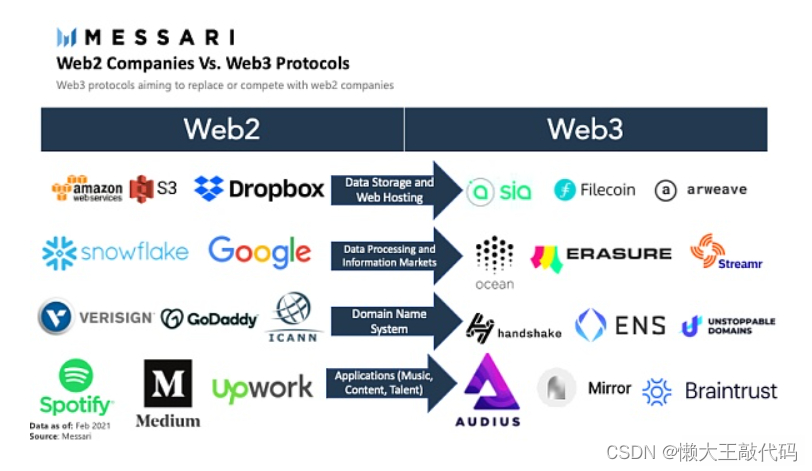
前端开发新趋势:Web3、区块链和虚拟现实
目录 前言 Web3:下一代互联网 区块链技术 去中心化应用程序(DApps) 区块链:重塑数字世界 数字钱包 NFT(非同质化代币) 虚拟现实:沉浸式体验 WebVR和WebXR 三维图形 新挑战与机会 性…...
如何安装运行Wagtail并结合cpolar内网穿透实现公网访问网站界面
文章目录 前言1. 安装并运行Wagtail1.1 创建并激活虚拟环境 2. 安装cpolar内网穿透工具3. 实现Wagtail公网访问4. 固定的Wagtail公网地址 前言 Wagtail是一个用Python编写的开源CMS,建立在Django Web框架上。Wagtail 是一个基于 Django 的开源内容管理系统…...
: fatal error RC1022: expected ‘#endif‘】)
【>D:\10\Debug\RCa00828(34): fatal error RC1022: expected ‘#endif‘】
1>D:\10\Debug\RCa00828(34): fatal error RC1022: expected ‘#endif’ The error message you’re seeing, fatal error RC1022: expected ‘#endif’, indicates that the resource compiler encountered an issue when processing a resource script file (typically w…...

使用vite搭建项目时,在启动vite后,浏览器显示页面:找不到localhost的网页
现象 在使用前端工具vite(版本5),搭建vue3项目时,启动vite,浏览器显示页面:找不到localhost的网页, 起初怀疑是 未加参数 --host0.0.0.0,导致,后加上该参数后问题依旧 解决 将index.html页面…...
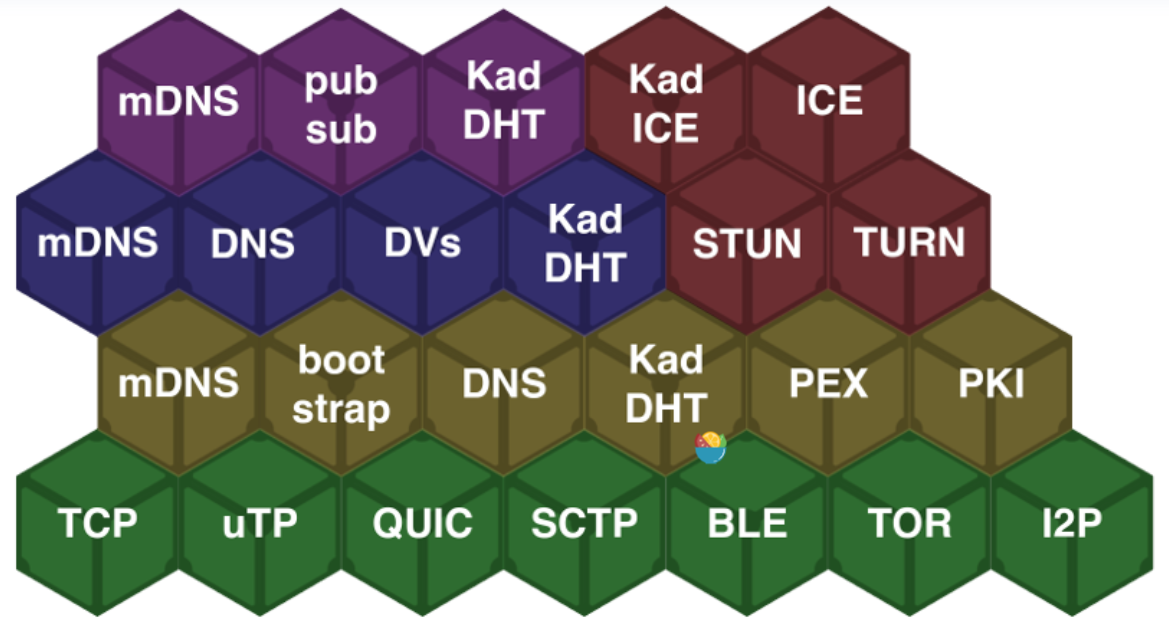
libp2p 快速开始
文章目录 第一部分:libp2p 快速入门一、什么是libp2plibp2p 发展历程libp2p的特性p2p 网络和我们熟悉的 client/server 网络的区别: 二、Libp2p的实现目标三、Libp2p的用途四、运行 Libp2p 协议流程libp2p 分为三层libp2p 还有一个局域网节点发现协议 mD…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
