2023-12-18 C语言实现一个最简陋的B-Tree
点击 <C 语言编程核心突破> 快速C语言入门
C语言实现一个最简陋的B-Tree
- 前言
- 要解决问题:
- 想到的思路:
- 其它的补充:
- 一、C语言B-Tree
- 基本架构:
- 二、可视化
- 总结
前言
要解决问题:
实现一个最简陋的B-Tree, 研究B-Tree的性质.
对于B树, 我是心向往之, 因为他是数据库的基石, 描述语言好像很容易理解, 但不造个轮子就不能彻底弄明白, 于是, 造个轮子.
想到的思路:
根据AI给的代码架子进行修改, 现在AI是个好东西, 虽说给的代码不一定靠谱, 但是debug一下, 还能深入了解, 总之是很有用.
其它的补充:
有一份C++ 的B-Tree, 是通过算法4的java代码移植的, 但是C++ 的内存管理教育了我, 太难整了, 于是一气之下, 全改为智能指针, 头疼的事就解决了. 也是很简陋的代码, 只有增查, 没有删改, 就暂时不提供了.
一、C语言B-Tree
基本架构:
为了适应不同的B-Tree节点, 通过宏BTREE_ORDER_SIZE 规定子节点的数量, 使用typedef int keyOfBTree;定义节点的key类型, 以适应不同需求.
BTreeNode的结构中, 对于值和子节点存储, 直接使用数组, 而不是指针, 好处是初始化的时候比较容易, free的时候也不容易出错, 毕竟都是数组, delete BTreeNode直接就完事了, 不用一个个的删除值, 省时间.
不好之处, 可能是自由度和空间利用度受限, 毕竟到最后叶子节点, 不管用不用子节点, 都要开辟子节点数组内存, 有一点点浪费.
打印节点内容以及释放树, 是用的递归, 毕竟这个用递归太容易了.
代码中最复杂的是分裂节点和向树中插入值, 需要慢慢体会, 多琢磨也不是太难.
至于删除节点和更改节点, 这里没有实现.
BTree.h头文件.
#ifndef BTREE_
#define BTREE_#include <stdint.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
对于B树, 如果形象的比喻, 就是拍平的二叉树, 并且是平衡二叉树, 每个节点可以容纳N个key, 同时容纳N+1个子节点, 这是一条非常重要的性质, 同时, 节点存放的key是按顺序排列的, 子节点也是按照顺序排列的, 是完全有序的.
一般子节点数量是偶数.
// B树的阶数,决定每个节点的孩子数量
#define BTREE_ORDER_SIZE 6
为了泛型, 我们只能用比较函数指针进行比较, 毕竟C语言不可能重载操作符.
// 比较函数指针类型
typedef int (*cmpFuncPtr)(void *, void *);
修改keyOfBTree可以让BTree使用不同的key
// 定义B树的key类型, 利于泛型
typedef int keyOfBTree;// 打印函数指针类型
typedef void (*printFun)(keyOfBTree);
B树的节点构成决定了其性质, B树含有一个key的数组, 以及子节点指针数组, 同时因为不一定数组全部是满的, 必须有一个num值指示究竟含有多少个key, 以及有多少个子节点, 也就是num + 1.
// B树的节点结构
typedef struct BTreeNode
{keyOfBTree keys[BTREE_ORDER_SIZE - 1]; // 关键字数组struct BTreeNode *childs[BTREE_ORDER_SIZE]; // 孩子节点指针数组uint32_t num; // 当前节点中的关键字数量int is_leaf; // 是否为叶子节点
} BTreeNode;typedef BTreeNode *BTree;
B树有一些必须接口, 也是不能再精简的接口包括节点创建, 查找索引, 在节点中插入值, 分裂节点, 在B树中插入值, 以及B树的释放. 打印B树是为了展示B树的结构, 在现实中, 一般是没有的.
// 创建节点
BTreeNode *createNode(int is_leaf);// 查找关键字在节点中的索引位置
int searchKeyIndex(BTreeNode *node, keyOfBTree key, cmpFuncPtr cmp);// 插入关键字到节点中的指定位置
void insertKey(BTreeNode *node, keyOfBTree key, cmpFuncPtr cmp);// 分裂一个满节点,将中间的关键字提升为父节点,并创建两个新的子节点
void splitNode(BTreeNode *parent, int child_index);// 在B树中插入关键字
void insert(BTreeNode **root, keyOfBTree key, cmpFuncPtr cmp);// 打印B树的关键字
void printBTree(BTreeNode *node, printFun printKey, int left, int *cnt);// 释放BTree
void freeBTree(BTreeNode **node);#endif
BTree.c实现.
#include "BTree.h"
创建节点很简单, 要给一个参数, 识别是不是叶子节点, 叶子节点不含任何子节点, 只含有值,
非叶子节点, 既有值又有子节点.
通过malloc分配内存, 初始化置零, 赋值是否为叶子节点.
// 创建节点
BTreeNode *createNode(int is_leaf)
{BTreeNode *node = (BTreeNode *)malloc(sizeof(BTreeNode));memset(node, 0, sizeof(BTreeNode));node->is_leaf = is_leaf;return node;
}
查找索引位置是B树的基本函数, 通过比较key和节点内部key数组中的值确定索引位置.
比如值是5, 节点内值数组是{1,3,8}, 用5和它们比较, 索引从0开始, 如果5大于1, 索引增加1, 大于3, 又增加1, 所以最终的索引值是2,
这个索引值非常重要, 通过它, 才能找到正确的子节点, 一步一步的深入找到最终的子节点.
// 查找关键字在节点中的索引位置
int searchKeyIndex(BTreeNode *node, keyOfBTree key, cmpFuncPtr cmp)
{int index = 0;while (index < node->num && cmp(&key, &(node->keys[index])) > 0){index++;}return index;
}
这个插入函数是在确定了究竟要在哪个子节点插入值后使用的, 过程需要挪动数组中的元素.
// 插入关键字到节点中的指定位置
void insertKey(BTreeNode *node, keyOfBTree key, cmpFuncPtr cmp)
{int index = (int)node->num - 1;while (index >= 0 && cmp(&key, &(node->keys[index])) < 0){node->keys[index + 1] = node->keys[index];index--;}node->keys[index + 1] = key;node->num++;
}
分裂节点比较复杂, 为了理解, 需要阐述一下
- 分裂的是父节点的子节点, 所以传入的是父节点指针以及子节点索引.
- 过程中会创建一个与子节点同样性质, 也就是是否是叶子节点的节点.
- 如果要分裂的子节点是叶子节点, 就不会分裂子节点的子节点, 因为没有, 否则值数组和子节点指针数组要同时分裂.
- 分裂会把子节点的中间值提升给父节点, 比如满值是
{1,2,3,4,5}, 那么就分裂为{1,2}{4,5}两个节点,3提升给父节点接收. - 被分裂的子节点的值数量
num以及父节点的num都要被修改.
// 分裂一个满节点,将中间的关键字提升为父节点,并创建两个新的子节点
void splitNode(BTreeNode *parent, int child_index)
{BTreeNode *child = parent->childs[child_index];BTreeNode *new_node = createNode(child->is_leaf);new_node->num = BTREE_ORDER_SIZE / 2 - 1;for (int i = 0; i < new_node->num; i++){new_node->keys[i] = child->keys[BTREE_ORDER_SIZE / 2 + i];}if (!child->is_leaf){for (int i = 0; i < BTREE_ORDER_SIZE / 2; i++){new_node->childs[i] = child->childs[BTREE_ORDER_SIZE / 2 + i];}}child->num = BTREE_ORDER_SIZE / 2 - 1;for (int i = (int)parent->num; i > child_index; i--){parent->childs[i + 1] = parent->childs[i];}parent->childs[child_index + 1] = new_node;for (int i = (int)parent->num - 1; i >= child_index; i--){parent->keys[i + 1] = parent->keys[i];}parent->keys[child_index] = child->keys[BTREE_ORDER_SIZE / 2 - 1];parent->num++;
}
向B树插入值, 过程也比较复杂, 需要阐述:
- 由于可能分裂根节点, 所以传入的是根节点的二级指针, 保证不丢失节点.
- 分三种情况, 根节点为空, 这个最简单, 直接生成节点, 在此节点插入值, 令根节点指向它.
- 根节点已满, 必须分裂根节点, 而为了分裂根节点, 需要给根节点整个父节点, 然后再将
root指针指向这个父节点, 并进行分裂. - 根节点非空非满, 如果根节点是叶子节点, 直接插入, 如果不是叶子节点, 那就要取得索引, 看索引地址的子节点是否是满的, 是则分裂, 然后进入子节点循环插入, 不是满的, 则直接进入子节点循环.
- 大家可能看出来了, 最终都是插入到叶子节点.
// 在B树中插入关键字
void insert(BTreeNode **root, keyOfBTree key, cmpFuncPtr cmp)
{BTreeNode *node = *root;// 如果根节点为空,则创建新的根节点if (node == NULL){*root = createNode(1);insertKey(*root, key, cmp);return;}// 如果根节点已满,则需要创建一个新的根节点if (node->num == BTREE_ORDER_SIZE - 1){BTreeNode *new_root = createNode(0);new_root->childs[0] = node;*root = new_root;splitNode(new_root, 0);insert(root, key, cmp); // 递归插入return;}// 如果根节点既非空也未满,直接插入while (1){if (node->is_leaf){insertKey(node, key, cmp);break;}int index = searchKeyIndex(node, key, cmp);if (node->childs[index]->num == BTREE_ORDER_SIZE - 1){splitNode(node, index);if (cmp(&key, &(node->keys[index])) > 0){index++;}}node = node->childs[index];}
}
打印B树, 可视化, 有利于理解B树的插入规律.
// 打印B树的关键字
void printBTree(BTreeNode *node, printFun printKey, int left, int *cnt)
{if (node){printf("%c%.2d([", "ABCDEFG"[left++], ++*cnt);for (int i = 0; i < node->num; i++){printKey(node->keys[i]);}printf("]);\n");if (!node->is_leaf){int leftL = left - 1;int cntL = *cnt;for (int i = 0; i <= node->num; i++){printf("%c%.2d==>", "ABCDEFG"[leftL], cntL);printBTree(node->childs[i], printKey, left, cnt);}printf("\n");}}
}
释放B树, 传入节点的二级指针, 最终确保随后节点指针指向NULL, 使用递归, 因为节点内部都是数组和整型值, 没有需要特殊处理的元素, 递归删除整个节点指针即可.
// 释放BTree
void freeBTree(BTreeNode **node)
{if (*node){// 非叶子节点必有子节点, 递归删除子节点if (!(*node)->is_leaf){// 子节点的数量不会大于key数量加1, 所以不用free child数组中所有节点;for (int i = 0; i <= (*node)->num; i++){freeBTree(&((*node)->childs[i]));}}free(*node);*node = NULL;}
}测试用例, 向B树插入32个区间在0-999的整数值, 打印成mermaid文本, 可在markdown软件下图形化.
#include "BTree.h"
#include <stdlib.h>#define SIZE 32void printKey(keyOfBTree key)
{printf("%d\t", key);
}int cmpInt(const int *lhs, const int *rhs)
{return *lhs - *rhs;
}int main()
{int arr[SIZE];for (int i = 0; i != SIZE; ++i){arr[i] = rand() % 1000;}// 创建一个空的B树BTree root = NULL;// 依次插入关键字for (int j = 0; j != SIZE; ++j){insert(&root, arr[j], (cmpFuncPtr)cmpInt);printf("```mermaid\ngraph TD;\nsubgraph BTree\n");int cnt = 0;// 打印B树printBTree(root, printKey, 0, &cnt);printf("end\n```\n\n");}// 释放内存freeBTree(&root);return 0;
}二、可视化
通过运行测试用例, 导出mermaid文本, 可以在markdown编辑器中实现可视化, 看随着输入, 树的分裂成长.
总结
通过以上的代码, 基本可以粗略了解B-Tree的性质,
就是树高增长缓慢,
单节点可以存储非常多的值,
查询速度优秀,
更贴近硬盘优化,
我们常见的数据库, mysql, sqlite, postgresql的基础都是B-Tree以及其变种, B+Tree,
了解底层, 期待更好的理解数据库, 在进行数据库设置时, 可以进行贴近底层的思考.
点击 <C 语言编程核心突破> 快速C语言入门
相关文章:

2023-12-18 C语言实现一个最简陋的B-Tree
点击 <C 语言编程核心突破> 快速C语言入门 C语言实现一个最简陋的B-Tree 前言要解决问题:想到的思路:其它的补充: 一、C语言B-Tree基本架构: 二、可视化总结 前言 要解决问题: 实现一个最简陋的B-Tree, 研究B-Tree的性质. 对于B树, 我是心向往之, 因为他是数据库的基…...
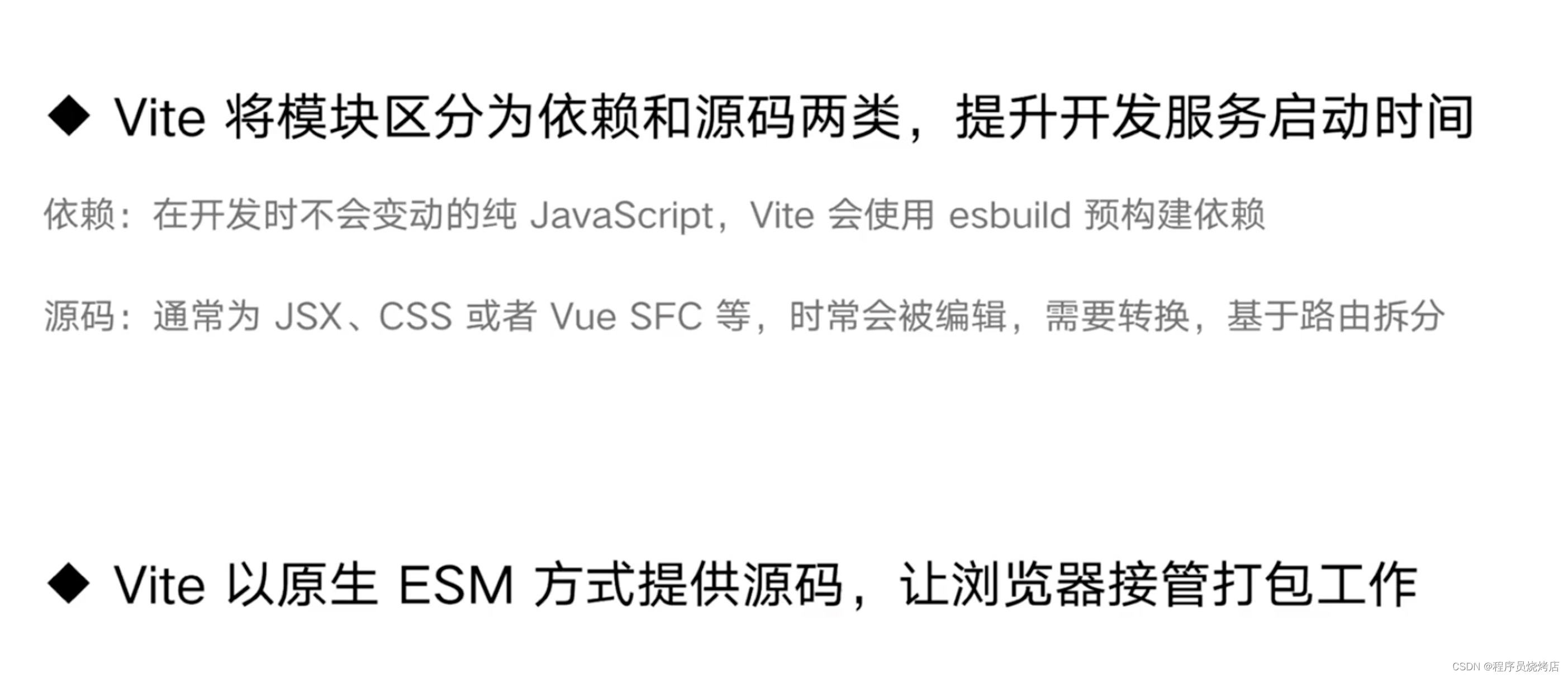
vite与webpack?
vite对比react-areate-app 1、构建速度 2、打包速度 3、打包文件体积...
算法和冲突驱动子句学习)
距离矩阵路径优化Python Dijkstra(迪杰斯特拉)算法和冲突驱动子句学习
Dijkstra算法 Dijkstra 算法是一种流行的寻路算法,通常用于基于图的问题,例如在地图上查找两个城市之间的最短路径、确定送货卡车可能采取的最短路径,甚至创建游戏地图。其背后的直觉基于以下原则:从起始顶点访问所有相邻顶点&am…...
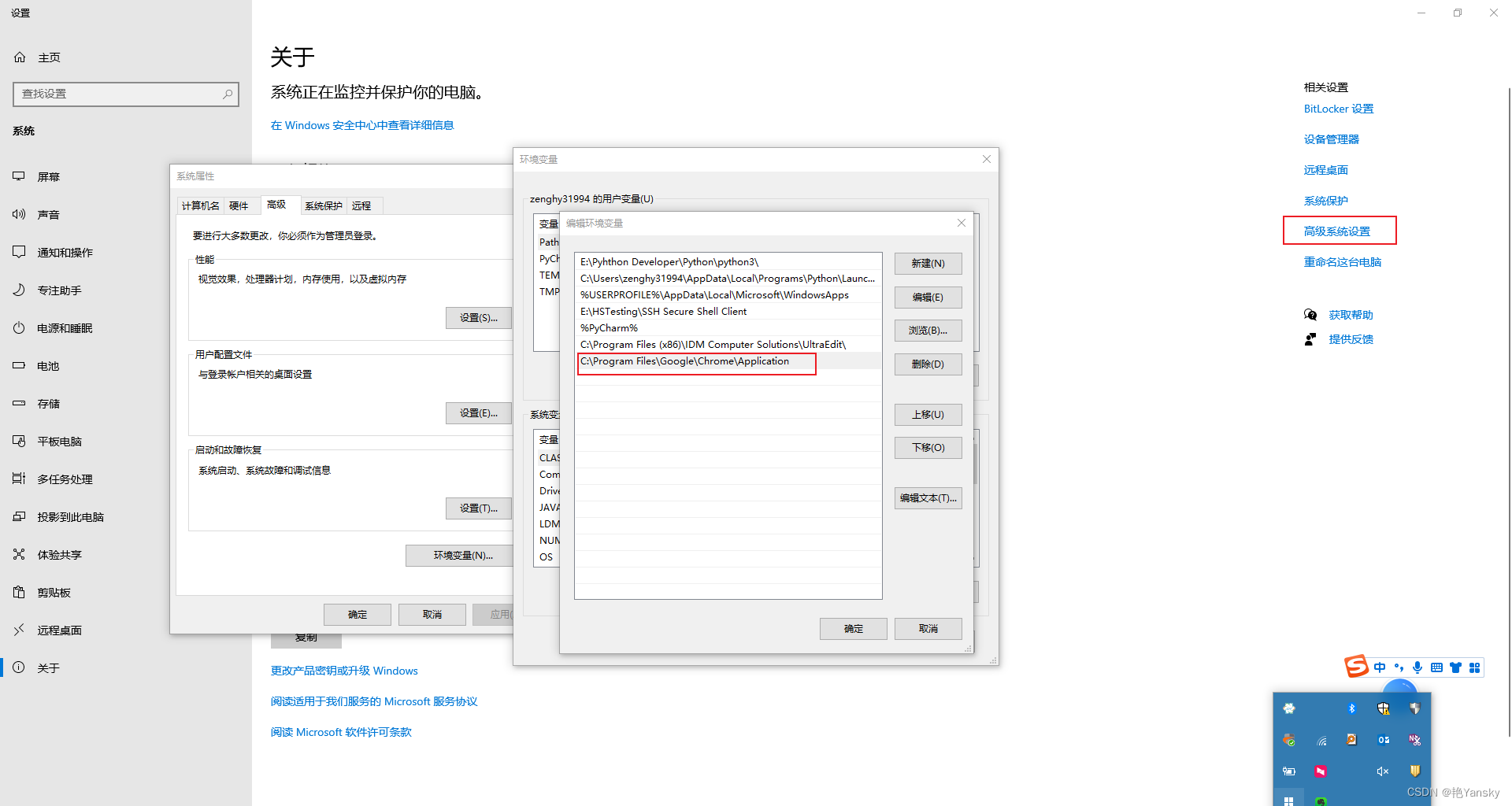
Selenium安装WebDriver:ChromeDriver与谷歌浏览器版本快速匹配_最新版120
最近在使用通过selenium操作Chrome浏览器时,安装中遇到了Chrome版本与浏览器驱动不匹配的的问题,在此记录安装下过程,如何快速找到与谷歌浏览器相匹配的ChromeDriver驱动版本。 1. 确定Chrome版本 我们首先确定自己的Chrome版本 Chrome设置…...
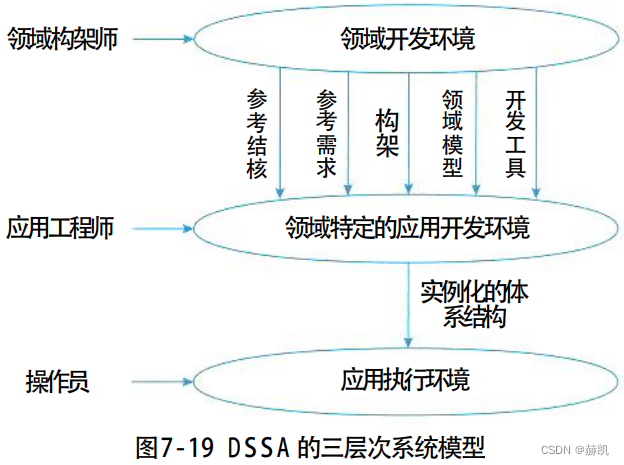
系统架构设计师教程(七)系统架构设计基础知识
系统架构设计基础知识 7.1 软件架构概念7.1.1 软件架构的定义7.1.2 软件架构设计与生命周期需求分析阶段设计阶段实现阶段构件组装阶段部署阶段后开发阶段 7.1.3 软件架构的重要性 7.2 基于架构的软件开发方法7.2.1 体系结构的设计方法概述7.2.2 概念与术语7.2.3 基于体系结构的…...
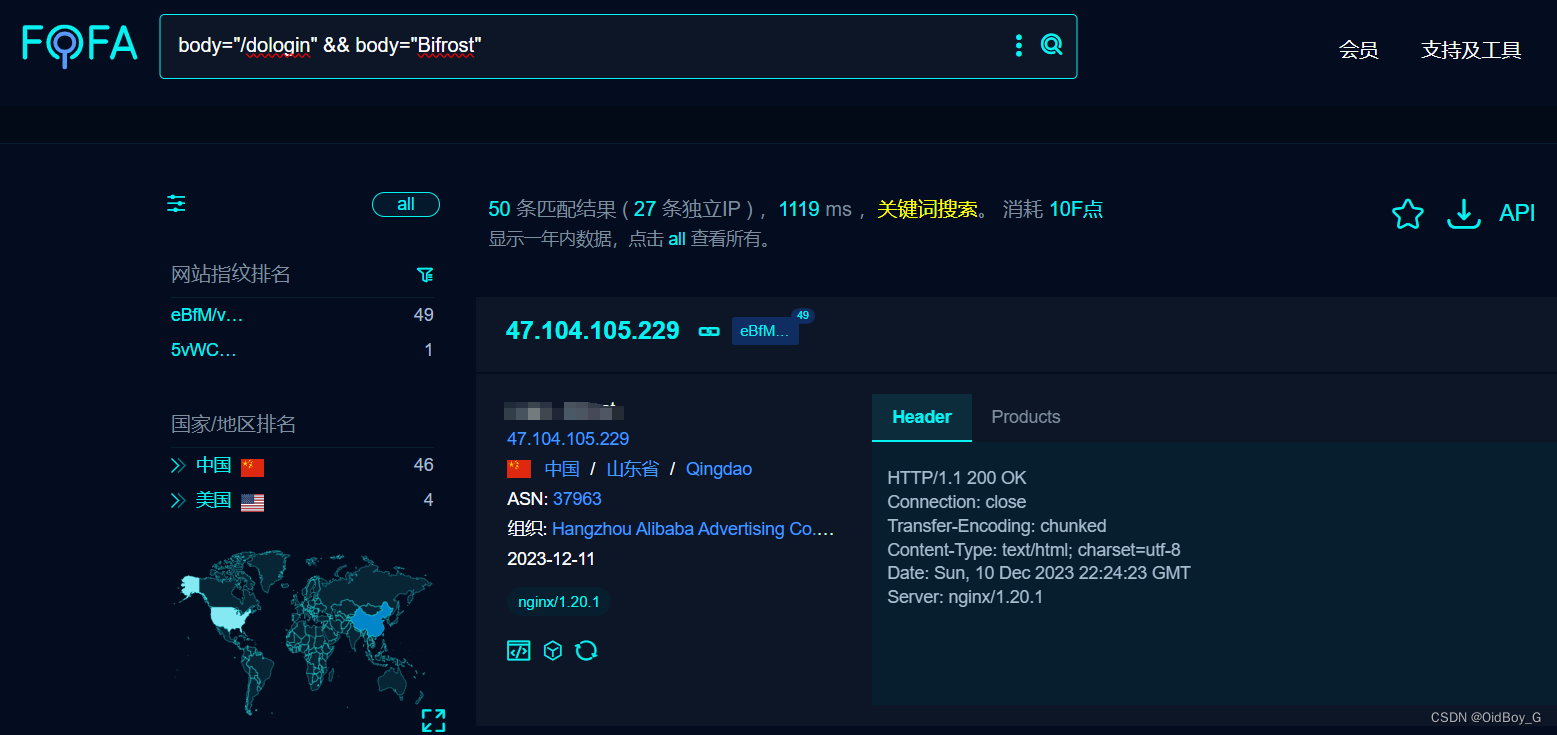
Bifrost 中间件 X-Requested-With 系统身份认证绕过漏洞复现
0x01 产品简介 Bifrost是一款面向生产环境的 MySQL,MariaDB,kafka 同步到Redis,MongoDB,ClickHouse等服务的异构中间件 0x02 漏洞概述 Bifrost 中间件 X-Requested-With 存在身份认证绕过漏洞,未经身份认证的攻击者可未授权创建管理员权限账号,可通过删除请求头实现身…...

OpenSSL 3.2.0新增Argon2支持——防GPU暴力攻击
1. 引言 OpenSSL新发布的3.20版本中,引入了一些新特性,包括: post-quantum方法Brainpool曲线QUICArgon2:Argon2 是一种慢哈希函数,在 2015 年获得 Password Hashing Competition 冠军,利用大量内存计算抵…...

数据结构--稀疏矩阵及Java实现
一、稀疏 sparsearray 数组 1、先看一个实际的需求 编写的五子棋程序中,有存盘退出和续上盘的功能。 分析问题: 因为该二维数组的很多值是默认值 0, 因此记录了很多没有意义的数据.->稀疏数组。 2、稀疏数组基本介绍 当一个数组中大部分元素为0…...
关于GPU使用过程中的若干问题
1.CUDA异常 问题描述:运行torch.cuda.is_available() 报错:cuda unknown error - this may be due to an incorrectly set up environment解决方案:重启 2.nvidia驱动版本不匹配 问题描述:运行nvidis-smi 报错:Fa…...
spring之面向切面:AOP(2)
学习的最大理由是想摆脱平庸,早一天就多一份人生的精彩;迟一天就多一天平庸的困扰。各位小伙伴,如果您: 想系统/深入学习某技术知识点… 一个人摸索学习很难坚持,想组团高效学习… 想写博客但无从下手,急需…...

【开题报告】基于uniapp的家庭记账小程序的设计与实现
1.研究背景 随着社会经济的发展和人们生活水平的提高,家庭财务管理变得越来越重要。家庭记账是一种重要的财务管理方式,通过记录和分析家庭的收入和支出情况,可以帮助家庭成员更好地理解和掌握自己的财务状况,合理规划和管理家庭…...

HTML5面试题
HTML5面试题 什么是HTML5?它与HTML4有何不同之处? HTML5是HTML的第五个主要版本,它引入了许多新的语义化元素、API和功能,以改进网页的结构、样式、交互和多媒体体验。 HTML5与HTML4的不同之处包括: 引入了一系列新的语…...

树莓派通过网线连接电脑并且设置设置链接wifi
好久没玩过树莓派了,系统进不去了,需要记录一下,之前总觉得自己会了,但是还是需要不断的翻阅资料。 树莓派 配置SD卡开启ssh - 哔哩哔哩 树莓派通过网线连接ssh 直接在sd卡建立一个ssh的文件,不要带任何后戳 ip查…...

C#拼接JSON
一、业务背景 最近项目需要与U8c对接,实现增删改查,借此机会,梳理一下C#解析Json字符串的问题。 这篇文章,先以新增接口为例。 二、新增接口 查看需要传入的json格式。 拼接json,无非就是{}和[]的来回嵌套。 首先&am…...

评价机器学习模型的指标
为了衡量一个机器学习模型的好坏,需要给定一个测试集,用模型对测试集中的每一个样本进行预测,并根据预测结果计算评价分数。 对于分类问题,常见的评价标准有准确率、精确率、召回率和F值等。给定测试集 𝒯 {(…...
C# WPF上位机开发(日志调试)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 程序开发的过程中,调试肯定是少不了的。比如说,这个时候,我们可以设置断点、查看变量、检查函数调用堆栈等等。…...

AR室内导航如何实现?技术与原理分析
随着科技的进步,我们生活中许多方面正在被重新定义。其中之一就是导航,尤其是室内导航。增强现实(AR)技术的出现为室内导航带来了革命性的变革。本文将深入探讨AR室内导航的技术与原理,以及它如何改变我们的生活方式。…...

计算机网络:物理层(奈氏准则和香农定理,含例题)
带你速通计算机网络期末 文章目录 一、码元和带宽 1、什么是码元 2、数字通信系统数据传输速率的两种表示方法 2.1、码元传输速率 2.2、信息传输速率 3、例题 3.1、例题1 3.2、例题2 4、带宽 二、奈氏准则(奈奎斯特定理) 1、奈氏准则简介 2、…...

天津仁爱学院专升本化学工程与工艺专业 《无机化学》考试大纲
天津仁爱学院化学工程与工艺专业高职升本入学考试《无机化学》课程考试大纲 一.参考教材 杨宏孝《无机化学简明教程》以及《无机化学简明教程学习指南》,高等教育出版社,2011年版。 二.考试基本要求 本考试要求将《无机化学》…...
GO 的 socks5代理 编写
这里学习一下 socks5 代理的编写 网上有很多 学习一下 go 语言实战入门案例之实现Socks5 - 知乎 滑动验证页面 socks5协议原理学习-腾讯云开发者社区-腾讯云 (tencent.com) 首先我们要了解一下socks5的代理方式 socks5 是基于 认证建立连接转发数据 所形成的代理 我们只…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
