核和值域的关系:什么是矩阵的秩?
核和值域的关系:什么是矩阵的秩?
这篇博客将介绍一个任意矩阵的核和值域的关系,并由此说明矩阵秩的意义、子空间维数、子空间正交。
1、矩阵的核:N(A)
A ∈ C m × n A\in C^{m\times n} A∈Cm×n,矩阵的核,记作N(A),N是nullity的首字母。
N ( A ) = { x ∣ A x = 0 , x ∈ C n } N(A)=\{x|Ax=0,x\in C^n \} N(A)={x∣Ax=0,x∈Cn}
A的核,其实就是齐次方程组Ax=0的所有解(解空间)。下面介绍解的情况。
- rank(A)=n,则有唯一解,且唯一解为0,N(A)={0}。
- rank(A)=r<n,则有无穷多解,且基本未知数个数为r,自由未知数个数为n-r,dim(N(A))=n-r。
可用行阶梯形来理解上述定理。注意,行初等变换不改变矩阵的解空间。
A x = 0 ⇒ A ~ x = 0 A ~ = [ a 1 , 1 a 1 , 2 a 1 , 3 … a 1 , n a 2 , 2 a 2 , 3 … a 2 , n ⋮ ⋱ ⋱ ⋮ ( 0 ) ⋱ a n − 1 , n 0 ⋯ a n , n ] Ax=0 \Rightarrow \tilde Ax=0\\ {\mathbf {\tilde A}}={\begin{bmatrix}a_{{1,1}}&a_{{1,2}}&a_{{1,3}}&\ldots &a_{{1,n}}\\ &a_{{2,2}}&a_{{2,3}}&\ldots &a_{{2,n}}\\ \vdots &&\ddots &\ddots &\vdots \\ &(0)&&\ddots &a_{{n-1,n}}\\ 0&&\cdots &&a_{{n,n}}\end{bmatrix}} Ax=0⇒A~x=0A~= a1,1⋮0a1,2a2,2(0)a1,3a2,3⋱⋯……⋱⋱a1,na2,n⋮an−1,nan,n
当rank(A)=n时,a_nn ≠ 0,因此x_n=0;关注第n-1行: a n − 1 , n − 1 x n − 1 + a n − 1 , n x n = 0 a_{n-1,n-1}x_{n-1}+a_{n-1,n}x_{n}=0 an−1,n−1xn−1+an−1,nxn=0,连锁反应将使得x_i=0, i=1~n;
当rank(A)=r是,a_rr ≠ 0,因此x_r=0,所以x=[0,0,0,*,*,*],r个0,n-r个任意值。
2、矩阵的值域:R(A)
A ∈ C m × n A\in C^{m\times n} A∈Cm×n,矩阵的值域,记作R(A),R是range的首字母。
R ( A ) = { y ∈ C m ∣ y = A x , x ∈ C n } R(A)=\{y\in C^m|y=Ax,x\in C^n \} R(A)={y∈Cm∣y=Ax,x∈Cn}
值域就是A的列向量组所能张成的最大空间。
- dim(R(A)) = rank(A) = rank(AH) = dim(R(AH))
- 秩-零化度定理:rank(A)+nullity(A)=n,nullity(A)=dim(N(A))
可以从线性表出的角度去理解。注意,矩阵的分块乘法。
y = A x = ( α 1 , α 2 , ⋯ , α n ) ( x 1 , x 2 , ⋯ , x n ) T = x 1 α 1 + x 2 α 2 + ⋯ + x n α n \begin{aligned} y &=Ax \\ &= (\alpha_1,\alpha_2,\cdots,\alpha_n)(x_1,x_2,\cdots,x_n)^T\\ &= x_1\alpha_1+x_2\alpha_2+\cdots+x_n\alpha_n \end{aligned} y=Ax=(α1,α2,⋯,αn)(x1,x2,⋯,xn)T=x1α1+x2α2+⋯+xnαn
3、子空间正交
所谓子空间正交,就是子空间W1的所有向量和W2所有向量正交。
< y , x > = < A x , x > = ( A x ) H x = x H A H x <y,x>=<Ax,x>=(Ax)^Hx=x^HA^Hx <y,x>=<Ax,x>=(Ax)Hx=xHAHx
因此R(A)和N(AH)正交。
- $R(A) \cap N(A^H)={0} $
- R ( A ) ⊕ N ( A H ) = C m R(A) \oplus N(A^H) = C^m R(A)⊕N(AH)=Cm
⊕ \oplus ⊕是直和,只有两个正交的空间才能进行直和运算。
直和:对于V1+V2中任何一个向量a=a1+a2,其中a1属于V1,a2属于V2,这种表示是唯一的,则称V1+V2为直和。
4、子空间维数定理
V 1 + V 2 = { x 1 + x 2 ∣ x 1 ∈ V 1 , x 2 ∈ V 2 } V 1 ∩ V 2 = { x ∣ x ∈ V 1 , x ∈ V 2 } V_1+V_2=\{x_1+x_2|x_1\in V_1,x_2\in V_2 \}\\ V_1\cap V_2=\{x|x\in V_1,x\in V_2 \} V1+V2={x1+x2∣x1∈V1,x2∈V2}V1∩V2={x∣x∈V1,x∈V2}
子空间维数定理:
d i m ( V 1 ) + d i m ( V 2 ) = d i m ( V 1 + V 2 ) + d i m ( V 1 ∩ V 2 ) dim(V_1)+dim(V_2)=dim(V_1+V_2)+dim(V1\cap V_2)\\ dim(V1)+dim(V2)=dim(V1+V2)+dim(V1∩V2)
可从三维空间理解。V1和V2是两个不相同的平面,各自维数为2,相加为4。和空间为整个三维空间,交空间为一条直线,即一维空间。
5、非齐次线性方程组的解
在第一节介绍了其次线性方程组Ax=0的解,下面介绍非齐次线性方程组Ax=b的解,其中 A ∈ C m × n A\in C^{m\times n} A∈Cm×n, A ˉ = [ A , b ] \bar A=[A,b] Aˉ=[A,b]是增广矩阵。
- 如果rank(A)=rank( A ˉ \bar A Aˉ)=n,则方程组有唯一解。
- 如果rank(A)=rank( A ˉ \bar A Aˉ)=r<n,则方程组有无穷多解。解空间维数为r,即基本未知数有r个,自由未知数有n-r个。
- 如果rank(A)<rank( A ˉ \bar A Aˉ),则方程组无解,解空间为空。
- 不存在rank(A)>rank( A ˉ \bar A Aˉ)
注意,齐次方程组必定有解,而非齐次方程组可能无解。
相关文章:

核和值域的关系:什么是矩阵的秩?
核和值域的关系:什么是矩阵的秩? 这篇博客将介绍一个任意矩阵的核和值域的关系,并由此说明矩阵秩的意义、子空间维数、子空间正交。 1、矩阵的核:N(A) A ∈ C m n A\in C^{m\times n} A∈Cmn,矩阵的核,记…...

【MyBatis Plus】Service Mapper内置接口讲解
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是Java方文山,一个在CSDN分享笔记的博主。📚📚 🌟推荐给大家我的专栏《MyBatis-Plus》。🎯🎯 &am…...
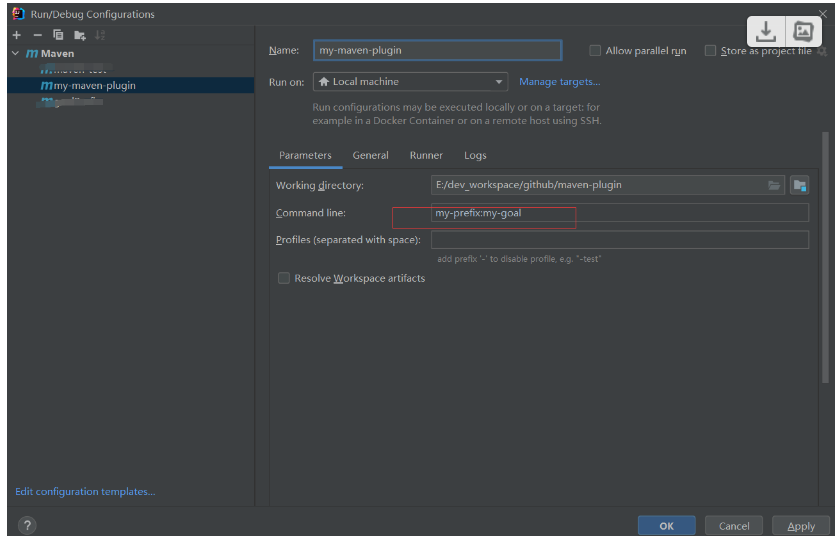
制作一个简单 的maven plugin
流程 首先, 你需要创建一个Maven项目,推荐用idea 创建项目 会自动配置插件 pom.xml文件中添加以下配置: <project> <!-- 项目的基本信息 --> <groupId>com.example</groupId> <artifactId>my-maven-plugi…...
基于linux系统的Tomcat+Mysql+Jdk环境搭建(三)centos7 安装Tomcat
Tomcat下载官网: Apache Tomcat - Which Version Do I Want? JDK下载官网: Java Downloads | Oracle 中国 如果不知道Tomcat的哪个版本应该对应哪个版本的JDK可以打开官网,点击Whitch Version 下滑,有低版本的,如…...

Ubuntu环境下SomeIP/CommonAPI环境搭建详细步骤
环境搭建 1.Boost安装 下载Boost源码 : https://www.boost.org/users/download/ 编译安装 首先安装编译所需依赖 sudo apt-get install build-essential g sudo apt-get install installpython-dev autotools-dev sudo apt-get install installlibicu-dev buil…...
maven 项目导入异常问题
问题如下 一、 tomcat正再运行的包是哪一个 不同构建、打包情况下分别运行 out\artifacts下 当直接去Project Structure下去构建artifacts 后,运行tomcat 则会在out下target下 reimport项目后,则会在artifacts自动生成部署包。删除tomcat之前deployment 下的包(同…...

在 VMware 虚拟机上安装黑苹果(Hackintosh):免费 macOS ISO 镜像下载及安装教程
在 VMware 虚拟机上安装黑苹果(Hackintosh):免费 macOS ISO 镜像下载及安装教程 VMware 虚拟机解锁 macOS 安装选项使用 macOS iso 系统镜像安装使用 OpenCore 做引导程序安装 在 VMware 虚拟机上安装黑苹果(Hackintosh):免费 macOS ISO 镜像下载及安装…...
国产ToolLLM的课代表---OpenBMB机构(清华NLP)旗下ToolBench的安装部署与运行(附各种填坑说明)
ToolBench项目可以理解为一个能直接提供训练ToolLLM的平台,该平台同时构建了ToolLLM的一个开源训练指令集。,该项目是OpenBMB机构(面壁智能与清华NLP联合成立)旗下的一款产品,OpenBMB机构名下还同时拥有另外一款明星产…...
-C#串口通信数据接收不完整解决方案)
串口通信(5)-C#串口通信数据接收不完整解决方案
本文讲解C#串口通信数据接收不完整解决方案。 目录 一、概述 二、Modbus RTU介绍 三、解决思路 四、实例 一、概述 串口处理接收数据是串口程序编写的关键...

大数据分析岗是干什么的?
大数据分析岗主要负责从大规模数据集中提取、整理、分析和解释有关业务、市场或其他相关领域的信息的职位。 主要的职责和工作内容如下: 1. 数据收集和整理 收集各种数据源(包括结构化、非结构化和半结构化数据),并将其整理成可…...

hadoop运行jar遇到的一个报错
报错信息: 2023-12-19 14:28:25,893 INFO mapreduce.Job: Job job_1702967272525_0001 failed with state FAILED due to: Application application_1702967272525_0001 failed 2 times due to AM Container for appattempt_1702967272525_0001_000002 exited with…...
长短期记忆(LSTM)神经网络-多输入分类
目录 一、程序及算法内容介绍: 基本内容: 亮点与优势: 二、实际运行效果: 三、部分程序: 四、完整程序下载: 一、程序及算法内容介绍: 基本内容: 本代码基于Matlab平台编译&am…...

开启创意之旅:免费、开源的噪波贴图(noise texture)生成网站——noisecreater.com详细介绍
在当今数字创意领域,噪波贴图(Noise Texture)是游戏渲染、游戏开发、美术设计以及影视制作等行业不可或缺的艺术素材之一。为了满足广大创作者的需求,noisecreater.com应运而生,成为一款免费、开源的噪波贴图生成工具。…...
Android Studio问题解决:Gradle Download 下载超时 Connect reset
文章目录 一、遇到问题二、解决办法 一、遇到问题 Gradle Download下载超时Sync了很多次,一直失败 二、解决办法 手动通过gradle网站下载 https://gradle.org/releases/可能也会出现超时,最好开个VPN软件会比较快。 下载好的软件,放到本机的…...

【Python百宝箱】云上翱翔:Python编程者的AWS奇妙之旅
雲端箴言:用Python主持AWS管理交響樂 前言 随着云计算的普及,AWS(Amazon Web Services)成为了许多组织和开发者首选的云服务提供商。作为Python工程师,深入了解AWS管理工具和库对于高效利用云资源至关重要。本文将引…...
抖音直播间websocket礼物和弹幕消息推送可能出现重复的情况,解决办法
在抖音直播间里,通过websocket收到的礼物消息数据格式如下: {common: {method: WebcastGiftMessage,msgId: 7283420150152942632,roomId: 7283413007005207308,createTime: 1695803662805,isShowMsg: True,describe: 莎***:送给主播 1个入团卡,priority…...

【设计模式--行为型--访问者模式】
设计模式--行为型--访问者模式 访问者模式定义结构案例优缺点使用场景扩展分派动态分派静态分派双分派 访问者模式 定义 封装一些作用于某种数据结构中的各元素的操作,它可以在不改变这个数据结构的前提下定义作用于这些元素的新操作。 结构 抽象访问者角色&…...
[最后一个月征稿、ACM独立出版】第三届密码学、网络安全和通信技术国际会议(CNSCT 2024)
第三届密码学、网络安全和通信技术国际会议(CNSCT 2024) 2024 3rd International Conference on Cryptography, Network Security and Communication Technology 一、大会简介 随着互联网和网络应用的不断发展,网络安全在计算机科学中的地…...

android —— PopupWindow
一、常用方法: 1、设置显示的位置 // 一个参数 popupWindow.showAsDropDown(v); //参数1: popupWindow关联的view // 参数2和3:相对于关联控件的偏移量popupWindow.showAsDropDown(View anchor, int xoff, int yoff)2、是否会获取焦点 popupWindow.se…...
mysql部署 --(docker)
先查找MySQL 镜像 Docker search mysql ; 拉取mysql镜像,默认拉取最新的; 创建mysql容器,-p 代表端口映射,格式为 宿主机端口:容器运行端口 -e 代表添加环境变量,MYSQL_ROOT_PASSWORD是root用户…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...
