Java 数据结构篇-实现堆的核心方法与堆的应用(实现 TOP-K 问题:最小 k 个数)
🔥博客主页: 【小扳_-CSDN博客】
❤感谢大家点赞👍收藏⭐评论✍


文章目录
1.0 堆的说明
2.0 堆的成员变量及其构造方法
3.0 实现堆的核心方法
3.1 实现堆的核心方法 - 获取堆顶元素 peek()
3.2 实现堆的核心方法 - 下潜 down(int i)
3.3 实现堆的核心方法 - 交换元素 swap(int i,int j)
3.4 实现堆核心方法 - 删除堆顶元素 poll()
3.5 实现堆的核心方法 - 替换堆顶元素 replace(int i)
3.6 实现堆的核心方法 - 添加元素 offer(int value)
3.7 实现堆的核心方法 - 建堆 heapify()
3.8 实现堆的核心方法完整代码
4.0 TOP - K 问题:最小的 K 个数
4.1 实现最小 k 个数的思路
4.2 代码实现最小 k 个数
1.0 堆的说明
堆(Heap)是一种基于树的数据结构,通常用于动态分配内存空间。堆可以被看作是一棵完全二叉树,其中每个节点都满足堆的性质,即父节点的值大于或等于子节点的值(大根堆),或父节点的值小于或等于子节点的值(小根堆)。在堆中,根节点的值是最大或最小的,因此也被称为最大堆或最小堆。
堆的实现通常使用数组来存储堆中的元素,通过计算数组下标来实现节点之间的关系。堆的时间复杂度为 O(log n),其中 n 是堆中元素的数量。
堆的操作包括插入、删除和查找等。插入操作将一个新元素插入到堆中,删除操作将堆中的最大或最小元素删除,查找操作可以在堆中查找特定元素的位置。
2.0 堆的成员变量及其构造方法
主要的成员变量为:int[] arr 数组:用来存放元素的容器;int size :代表当前的元素个数。
构造方法:指定数组大小带参数的构造器、参数为数组的构造器。
代码如下:
public class MyHeap {public int[] arr;public int size;public MyHeap(int capacity) {arr = new int[capacity];}public MyHeap(int[] arr) {this.arr = arr;this.size = arr.length;heapify();}}
3.0 实现堆的核心方法
获取堆顶元素、下潜、交换元素、添加元素、替换元素、删除元素、建堆。
3.1 实现堆的核心方法 - 获取堆顶元素 peek()
用数组实现堆,在获取堆顶元之前,先需要判断该数组是否为空,若不为空,则直接返回数组索引为 0 的元素;若数组为空,则返回 0 或者抛出异常也可以。
代码如下:
//获取栈顶元素public int peek() {if (isEmpty()) {return -1;}return arr[0];}
3.2 实现堆的核心方法 - 下潜 down(int i)
该方法主要用于删除栈顶元素、替换元素等核心方法。下潜的意思就是将当前的元素所在的位置不符合大顶堆或者小顶堆的规则,因此需要向下调整。找到合适的位置来存放当前的元素。
具体下潜的思路:
假设需要满足大顶堆的规则:
由以上的图来看,当前的索引为 0 处的元素 7 小于该左孩子的元素,因此当前不满足大顶堆的规则。需要将两者进行交换。
交换的结果为:
交换完之后,当前索引为 2 处的元素 7 小于该右孩子的元素,所以索引 2 与 索引 5 需要继续交换。若当前为 i 该右孩子的索引 left = 2 * i + 1;该左孩子的索引 right = 2 * i + 2 (也可以表示为 right = left + 1 )一开始默认当前的最大元素的索引 max = i ,接着来判断该左右孩子的元素是否大于当前索引 max ,若大于当前索引 max 时,需要进行交换 max = left 或者 max = right 。若不大于当前索引为 max 处的元素,则不需要交换。由于每一次都是子问题过程,所以可以利用递归来实现,当且仅当 max != i 时,说明 max 已经被交换过了,需要继续向下递出,直到 max == i 时,结束递出,开始回溯。当然,这里不需要回带任何值或者变量,即该递归函数的返回类型为 viod 。
代码如下:
//下潜public void down(int i) {int left = 2 * i + 1;int right = left + 1;int max = i;if (left < size && arr[left] > arr[max]) {max = left;}if (right < size && arr[right] > arr[max]) {max = right;}if (max != i) {//交换swap(i,max);//继续下潜down(max);}}
3.3 实现堆的核心方法 - 交换元素 swap(int i,int j)
交换数组索引中 i 与 j 处的元素。
代码如下:
//交换public void swap(int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}
3.4 实现堆核心方法 - 删除堆顶元素 poll()
具体实现思路:为了更高效率的删除堆顶元素后保持原来大顶堆或者小顶堆的规则。
步骤一:先将堆顶元素与最后一个元素进行交换。即 arr[0] = arr[size - 1] 。
步骤二:将 size-- 。
步骤三:交换后的堆,可能会不满足大顶堆或者小顶堆的规则,则需要将堆顶元素进行下潜调整,找到合适的位置存放该元素。最后需要返回删除的元素。
代码如下:
//删除堆顶元素public int poll() {if (isEmpty()) {return 0;}int t = arr[0];arr[0] = arr[size - 1];size--;//下潜down(0);return t;}注意:在删除堆顶元素之前,需要先判断当前的数组是否为空数组。
同理,若需要删除指定堆中的元素索引,实现思路是一样的。
代码如下:
//指定删除元素public int poll(int i) {if (i > size) {return 0;}int temp = arr[i];arr[i] = arr[size - 1];size--;//下潜down(i);return temp;}先判断索引是否合法,若不合法,则返回 0 或者抛出异常也可以。
3.5 实现堆的核心方法 - 替换堆顶元素 replace(int i)
具体思路为:先判断该数组是否为空数组,若不为空数组,则直接替换堆顶元素 arr[0] = i;之后可能会不满足大顶堆或者小顶堆的规则,所以索引为 0 处需要下潜调整,找到合适的位置存放元素。
代码实现:
//替换堆顶元素public void replace(int i) {if (isEmpty()) {return;}arr[0] = i;down(0);}
3.6 实现堆的核心方法 - 添加元素 offer(int value)
具体实现思路:先判断当前索引为 i = size 处的双亲节点为 j = (i - 1) / 2 ,判断 arr[j] 与 value 的大小,若为大顶堆规则,则当 arr[j] > value 时,不需要继续往上走了,在 i 处存放 value 即可 arr[i] = value ;当 arr[j] <= value 时,先将 arr[j] 处的元素存放在 arr[i] 中,接着需要继续往上走, i = j ,j = (i - 1) / 2 直到 i == 0 或者 arr[j] > value 时,退出循环。在 arr[i] 处存放 value 。
代码如下:
//添加元素public boolean offer(int value) {if (isFull()) {return false;}int i = size;int j = (size - 1) / 2;while (i > 0 && arr[j] < value) {arr[i] = arr[j];i = j;j = (i - 1) / 2;}arr[i] = value;size++;return true;}需要注意:添加元素前,需要先判断该数组是否满了。还有添加完之后,需要进行 size++ 。
3.7 实现堆的核心方法 - 建堆 heapify()
该方法实现的意义,若随机给出一个数组,需要实现由大顶堆或者小顶堆的结构存放元素。因此就会用到该方法。
实现思路为:需要找到最后一个非叶子节点,从后往前,将当前的元素进行下潜处理即可完成建堆。
代码如下:
//建堆public void heapify() {//先找到最后非叶子节点int lastNonLeafNodes = size / 2 - 1;for (int i = lastNonLeafNodes; i >= 0 ; i--) {//下潜down(i);}}
3.8 实现堆的核心方法完整代码
public class MyHeap {public int[] arr;public int size;public MyHeap(int capacity) {arr = new int[capacity];}public MyHeap(int[] arr) {this.arr = arr;this.size = arr.length;heapify();}//获取栈顶元素public int peek() {if (isEmpty()) {return -1;}return arr[0];}//删除堆顶元素public int poll() {if (isEmpty()) {return 0;}int t = arr[0];arr[0] = arr[size - 1];size--;//下潜down(0);return t;}//指定删除元素public int poll(int i) {if (i > size) {return 0;}int temp = arr[i];arr[i] = arr[size - 1];size--;//下潜down(i);return temp;}//替换堆顶元素public void replace(int i) {if (isEmpty()) {return;}arr[0] = i;down(0);}//添加元素public boolean offer(int value) {if (isFull()) {return false;}int i = size;int j = (size - 1) / 2;while (i > 0 && arr[j] < value) {arr[i] = arr[j];i = j;j = (i - 1) / 2;}arr[i] = value;size++;return true;}//建堆public void heapify() {//先找到最后非叶子节点int lastNonLeafNodes = size / 2 - 1;for (int i = lastNonLeafNodes; i >= 0 ; i--) {//下潜down(i);}}//下潜public void down(int i) {int left = 2 * i + 1;int right = left + 1;int max = i;if (left < size && arr[left] > arr[max]) {max = left;}if (right < size && arr[right] > arr[max]) {max = right;}if (max != i) {//交换swap(i,max);//继续下潜down(max);}}//交换public void swap(int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}//判断是否为空数组public boolean isEmpty() {return size == 0;}//判断是否为满数组public boolean isFull() {return size == arr.length;} }
4.0 TOP - K 问题:最小的 K 个数
题目:
设计一个算法,找出数组中最小的k个数。以任意顺序返回这 k 个数均可。
示例:
输入: arr = [1,3,5,7,2,4,6,8], k = 4 输出: [1,2,3,4]提示:
0 <= len(arr) <= 100000
0 <= k <= min(100000, len(arr))OJ 链接:
面试题 17.14. 最小K个数
4.1 实现最小 k 个数的思路
具体思路为:结合大顶堆的数据结构的特点,根节点的元素永远比孩子节点的元素大。先将给定的 arr 数组的前 k 个元素直接通过 heap.offer() 方法添加到大顶堆上,然后 arr 数组剩下的元素需要跟堆顶元素相对比,若堆顶元素大于 arr[i] 中的元素,则需要进行交换,将 arr[i] 的元素替换到堆顶,接着还不能结束,有可能替换完的元素就不符合大顶堆的规则了,因此还需要将堆顶元素下潜处理调整,找到合适的位置存放该元素;若堆顶元素不大于 arr[i] 中的元素,则不需要交换。一直将 arr 数组中的元素遍历结束,则循环停止。最后堆上存储的 k 个元素就是该数组 arr 中最小的元素了。
4.2 代码实现最小 k 个数
public class Solution {public int[] smallestK(int[] arr, int k) {MaxHeap heap = new MaxHeap(k);for(int i = 0; i < k ; i++) {heap.offer(arr[i]);}for(int i = k; i < arr.length; i++) {if(heap.peek() > arr[i]) {heap.arr[0] = arr[i];heap.down(0);}}return heap.arr;}}//实现一个大顶堆 class MaxHeap {int[] arr;int size;public MaxHeap(int capacity) {arr = new int[capacity];}public MaxHeap(int[] smallestK) {this.arr = smallestK;this.size = smallestK.length;}//插入元素public boolean offer(int value) {if(isFull()) {return false;}int i = size;int j = (i - 1) / 2;while(i > 0 && arr[j] < value) {arr[i] = arr[j];i = j;j = (i - 1) / 2;}arr[i] = value;size++;return true;}//删除堆顶元素public int poll() {if(isEmpty()) {return 0;}int ret = arr[0];arr[0] = arr[size - 1];size--;down(0);return ret;}//下潜public void down(int i) {int left = 2 * i + 1;int right = left + 1;int max = i;if(left < size && arr[left] > arr[max]) {max = left;}if(right < size && arr[right] > arr[max]) {max = right;}if(max != i) {swap(max,i);down(max);}}//交换public void swap(int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}//获取堆顶元素public int peek() {if(isEmpty()) {return 0;}return arr[0];}//判断是否为空public boolean isEmpty() {return size == 0;}//判断是否为满public boolean isFull() {return size == arr.length;}}
相关文章:
Java 数据结构篇-实现堆的核心方法与堆的应用(实现 TOP-K 问题:最小 k 个数)
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 文章目录 1.0 堆的说明 2.0 堆的成员变量及其构造方法 3.0 实现堆的核心方法 3.1 实现堆的核心方法 - 获取堆顶元素 peek() 3.2 实现堆的核心方法 - 下潜 down(int i) 3.3 实…...

startUML6.0.1破解方法
startUML6.0.1破解方法 文章目录 startUML6.0.1破解方法1.startUML6.0.1快速破解2.概述3.安装Nodejs4.安装asar5.修改app.asar中的源码6.将修改后的源码重新压缩7.覆盖官方的asar文件8.重启startUML9.参考文档 1.startUML6.0.1快速破解 后绪步骤可以不看,直接下载我…...

Python实现多种图像分割方法:基于阈值分割和基于区域分割
Python实现多种图像分割方法:基于阈值分割和基于区域分割 图像分割是图像分析的第一步,是计算机视觉的基础,但也是图像处理中最困难的问题之一。经典的计算机视觉任务,如目标检测、图像识别等都和图像分割相关,图像分…...

SQL学习笔记+MySQL+SQLyog工具教程
文章目录 1、前言2、SQL基本语言及其操作2.1、CREATE TABLE – 创建表2.2、DROP TABLE – 删除表2.3、INSERT – 插入数据2.4、SELECT – 查询数据2.5、SELECTDISTINCT – 去除重复值后查询数据2.6、SELECTWHERE – 条件过滤2.7、AND & OR – 运算符2.8、ORDER BY – 排序2…...

SpringBoot的日志管理
🙈作者简介:练习时长两年半的Java up主 🙉个人主页:程序员老茶 🙊 ps:点赞👍是免费的,却可以让写博客的作者开心好久好久😎 📚系列专栏:Java全栈,…...

leetcode---76. 最小覆盖子串 [C++/滑动窗口+哈希表]
原题:76. 最小覆盖子串 - 力扣(LeetCode) 题目解析: 此题在这道题的基础上进行理解会更简单 leetcode --- 30. 串联所有单词的子串[C 滑动窗口/双指针]-CSDN博客 本题要求在s字符串中找到含有t字符串所有字符的最短子串。 也就是…...
Kafka 分级存储在腾讯云的实践与演进
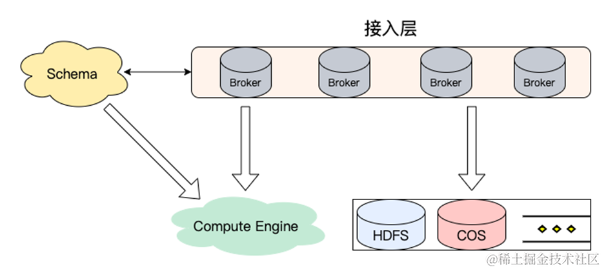
导语 腾讯云消息队列 Kafka 内核负责人鲁仕林为大家带来了《Kafka 分级存储在腾讯云的实践与演进》的精彩分享,从 Kafka 架构遇到的问题与挑战、Kafka 弹性架构方案类比、Kafka 分级存储架构及原理以及腾讯云的落地与实践四个方面详细分享了 Kafka 分级存储在腾讯云…...
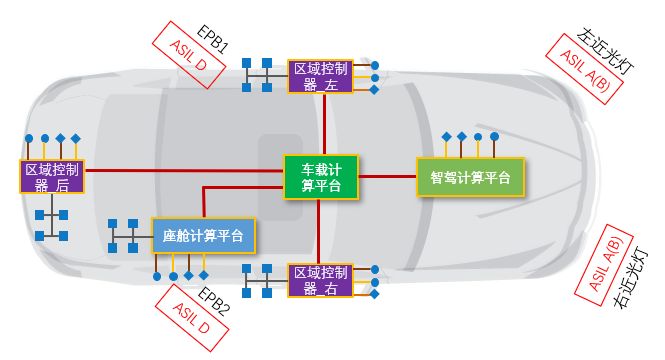
域架构下的功能安全思考
来源:联合电子 随着整车电子电气架构的发展,功能域控架构向整车集中式区域控制演进。新的区域控制架构下,车身控制模块(BCM),整车控制单元(VCU),热管理系统(TMS)和动力底…...

python多线程介绍
每个库或模块都有其特定的用途和优势,选择哪一个取决于具体的任务需求、计算资源。一般可以将任务分成两类: I/O 密集型任务:这些任务的瓶颈主要在于等待外部操作,如磁盘读写或网络通信。在这些等待期间,CPU 大部分时间…...

征文榜单 | 腾讯云向量数据库获奖名单公布
为了帮助开发者更快、更便捷地构建应用程序,有效提高开发人员生产力,腾讯云推出了AI原生向量数据库。它能提供全托管的自研企业级分布式数据库服务,专用于存储、检索、分析多维向量数据,是国内首个从接入层、计算层、到存储层提供…...
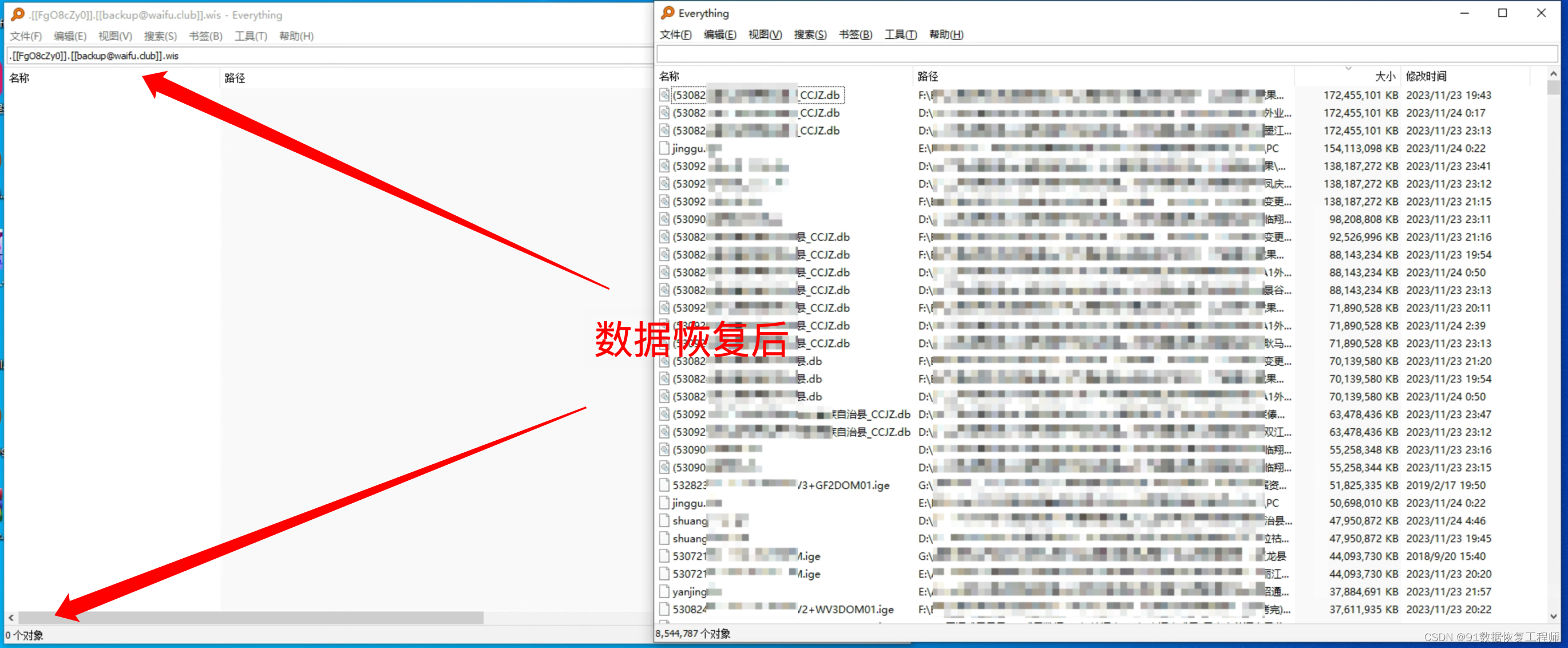
如何预防[[MyFile@waifu.club]].wis [[backup@waifu.club]].wis勒索病毒感染您的计算机?
导言: 近期,一种新兴的威胁[[MyFilewaifu.club]].wis [[backupwaifu.club]].wis勒索病毒,引起了广泛关注。这种恶意软件通过其高度复杂的加密算法,威胁着用户和组织的数据安全。本文将深入介绍[[MyFilewaifu.club]].wis [[backup…...

中国风春节倒计时【实时倒计时】
<head><meta charset="UTF-8"><meta name="apple-mobile-web-app-title...

基于RBAC的k8s集群权限管控案例
在日常的kubernetes集群维护过程中,常常涉及多团队协作,不同的团队有不同的操作和权限需求。比如,运维团队需要有node的所有操作权限,以便对集群进行节点的扩缩容等日常维护工作,但资产运营团队通常只需要node的查看权…...

【华为数据之道学习笔记】5-11 算法模型设计
算法是指训练、学习模型的具体计算方法,也就是如何求解全局最优解,并使得这个过程高效且准确,其本质上是求数学问题的最优化解,即算法是利用样本数据生成模型的方法。算法模型是根据业务需求,运用数学方法对数据进行建…...

Flink系列之:SELECT WHERE clause
Flink系列之:SELECT & WHERE clause 一、SELECT & WHERE clause二、SELECT DISTINCT 适用于流、批 一、SELECT & WHERE clause SELECT 语句的一般语法是: SELECT select_list FROM table_expression [ WHERE boolean_expression ]table_e…...

C#基础——委托、Action和Func的使用
1、委托 委托(Delegate)是一种类型,可以用来表示对一个或多个方法的引用。委托提供了一种方便的方式来将方法作为参数传递给其他方法,或将方法存储在数据结构中以供以后调用。 不带参数且没返回值的委托 delegate void HDLDelega…...
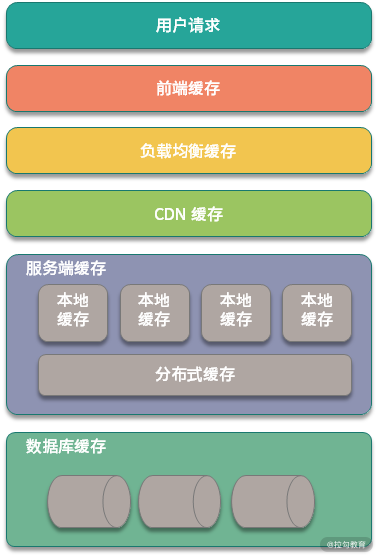
不止业务缓存,分布式系统中还有哪些缓存?
缓存是分布式系统开发中的常见技术,在分布式系统中的缓存,不止 Redis、Memcached 等后端存储;在前端页面、浏览器、网络 CDN 中也都有缓存的身影。 缓存有哪些分类 如果你是做业务开发的话,提起缓存首先想到的应该是应用 Redis&…...

Java 基础学习(十三)集合框架、List集合
1 集合框架 1.1 Collection 1.1.1 集合框架概述 Java 集合框架是一组实现了常见数据结构(如列表、树集和哈希表等)的类和接口,用于存储一组数据。 开发者在使用Java的集合类时,不必考虑数据结构和算法的具体实现细节ÿ…...

el-select二次封装实现可分页加载数据
使用el-select时一次性渲染几百条数据时会造成页面克顿, 可以通过分页来实现, 这里我用的方式为默认获取全部数据, 然后一次性截取10条进行展示, 滚动条触底后会累加, 大家也可以优化为滚动条触底后发送请求去加载数据 创建自定义指令customizeFocus用户懒加载 在utils文件夹(…...

css实现0.5px宽度/高度显——属性: transform: scale
在大多数设备上,实际上无法直接使用 CSS 来精确地创建 0.5 像素的边框。因为大多数屏幕的最小渲染单位是一个物理像素,所以通常只能以整数像素单位渲染边框。但是,有一些技巧可以模拟出看起来像是 0.5 像素的边框。 这里介绍使用:…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...


