工业6轴机械臂运动学逆解(解析解)
工业6轴机械臂运动学逆解(解析解)
通常工业机械臂采用6旋转轴串连的形式,保证了灵活性,但为其运动学逆解(即已知机械臂末端的位姿 P P P,求机械臂各个旋转轴的旋转角)带来了较大的困难,通常没有解析解。为了提高实时性,经过前辈们不懈的研究,当6轴机械臂满足pieper准则时,可以得出其运动学逆解的解析解。pieper准则如下:
- 三个相邻关节轴线交于一点,如fanuc m10系列;
- 三个相邻关节轴线相互平行,如ur5系列;
以下将通过一个简单实例,介绍机械臂在pieper第一准则的情况的运动学逆解。
机械臂运动学模型
机械臂的简化模型如图1所示。
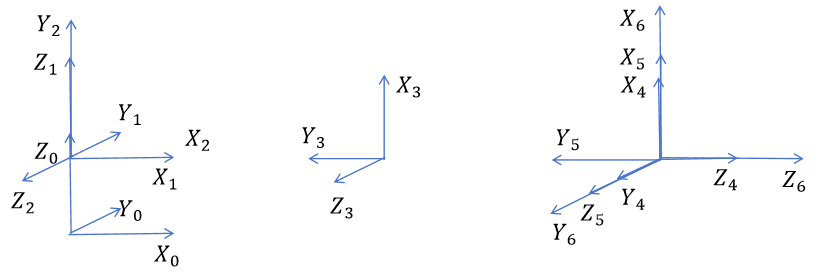
采用DH矩阵的形式对机械臂进行建模,DH矩阵如下:
| 关节 | 连杆夹角 | 连杆长度 | 连杆偏距 | 初始关节角 |
|---|---|---|---|---|
| 1 | 0 | 0 | 0.1 | 0 |
| 2 | 0.5 π \pi π | 0 | 0 | 0 |
| 3 | 0 | 0.5 | 0 | 0.5 π \pi π |
| 4 | 0.5 π \pi π | 0 | 0.5 | 0 |
| 5 | -0.5 π \pi π | 0 | 0 | 0 |
| 6 | 0.5 π \pi π | 0 | 0 | 0 |
从图1中可以看出,在初始状态下,机械臂的第2、3关节轴与基座坐标系的Y轴相互平行,机械臂的第4、5、6关节轴线相交于一点 P P P,满足pieper第一准则,且点 P P P与基座坐标系的XOZ平面重合。在这些条件下,虽然限制了机械臂的设计和构型,但极大地简化了逆解的过程。
运动学逆解
由于机械臂的结构比较简单,故采用几何法的方式求解机械臂的运动学逆解。
机械臂末端初始位姿 P 0 P_0 P0,运动学逆解末端的位姿 P ( x , y , z ) P(x,y,z) P(x,y,z)
求解第1关节轴的关节角
以基坐标系为参考,机械臂末端位置示意图如图2所示。

在图1中,点 P 0 P_0 P0为机械臂末端的初始状态位置(当前位置),点 P P P为机械臂末端的期望位置,由于初始状态时,机械臂末端的初始位置与 X 0 Y 0 X_0Y_0 X0Y0平面重合,故关节轴1需要旋转 θ 1 \theta_1 θ1或 θ 1 + π \theta_1 + \pi θ1+π才能使期望位置 P P P与 X 0 Y 0 X_0Y_0 X0Y0平面重合,故,关节轴1存在两个解
θ 1 = { a t a n 2 ( y , x ) a t a n 2 ( y , x ) + π (1) \theta_1 = \begin{cases} atan2(y, x)\\ atan2(y, x) + \pi\\ \end{cases} \tag1 θ1={atan2(y,x)atan2(y,x)+π(1)
求解第2、3关节轴的关节角
关节轴1经过旋转 θ 1 = a t a n 2 ( y , x ) \theta_1=atan2(y, x) θ1=atan2(y,x)角度,以第一关节轴的坐标系为参考,得示意图如图3所示。 P 1 P_1 P1为机械臂末端的当前位置, P P P为末端期望位置, O A 0 OA_0 OA0、 O A 1 OA_1 OA1为机械臂的第2连杆, A 0 P A_0P A0P、 A 1 P A_1P A1P为机械臂的第3连杆。
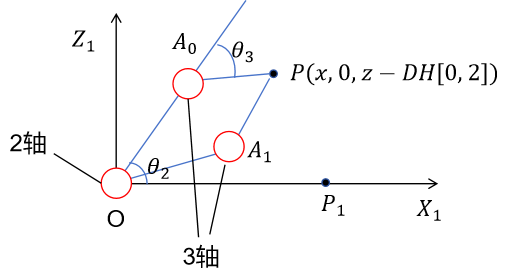
设 A 0 ( x 0 , 0 , z 0 ) A_0(x_0, 0, z_0) A0(x0,0,z0),可得方程:
x 0 2 + z 0 2 = D H [ 2 , 1 ] 2 ( x − x 0 ) 2 + ( z − D H [ 0 , 2 ] − z 0 ) 2 = D H [ 3 , 2 ] 2 (2) x_0^2 + z_0^2 = DH[2, 1]^2\\ (x - x_0)^2 + (z - DH[0, 2] - z_0)^2 = DH[3, 2]^2 \tag2 x02+z02=DH[2,1]2(x−x0)2+(z−DH[0,2]−z0)2=DH[3,2]2(2)
对2元2次方程组(2)进行求解,得 ( x 00 , z 00 ) (x_{00}, z_{00}) (x00,z00)、 ( x 01 , z 01 ) (x_{01}, z_{01}) (x01,z01)、 ( x 02 , z 02 ) (x_{02}, z_{02}) (x02,z02)、 ( x 03 , z 03 ) (x_{03}, z_{03}) (x03,z03)四组解,去除其中的非实数解。由此可得到关节轴2、3的旋转角。
θ 2 = a t a n 2 ( z 0 , x 0 ) θ 3 = a t a n 2 ( z − D H [ 0 , 2 ] − z 0 , x − x 0 ) − a t a n 2 ( z 0 , x 0 ) (2) \theta_2 = atan2(z_0, x_0)\\ \theta_3 = atan2(z - DH[0, 2] - z_0, x - x_0) - atan2(z_0, x_0) \tag2 θ2=atan2(z0,x0)θ3=atan2(z−DH[0,2]−z0,x−x0)−atan2(z0,x0)(2)
如图2所示,解方程(2),可得到关节角 θ 2 \theta_2 θ2、 θ 3 \theta_3 θ3的两组解。
同理,当取 θ 1 = a t a n 2 ( y , x ) + π \theta_1=atan2(y, x) + \pi θ1=atan2(y,x)+π时,亦可得到关节角 θ 2 \theta_2 θ2、 θ 3 \theta_3 θ3的两组解。
至此, θ 1 \theta_1 θ1、 θ 2 \theta_2 θ2、 θ 3 \theta_3 θ3存在8组解,可去除其中相同的解。
求解第4、5、6关节轴的关节角
经过对机械臂前3根轴的旋转,已经机械臂的末端位置与期望的末端位置相重合,由于关节轴4、5、6相交与末端位置,对此3轴的旋转不会改变末端的位置,故,单独对此3轴进行姿态解算即可得到关节角。
设 R 1 ( θ 1 ) R_1(\theta_1) R1(θ1)、 R 2 ( θ 2 ) R_2(\theta_2) R2(θ2)、 R 3 ( θ 3 ) R_3(\theta_3) R3(θ3)、 R 4 ( θ 4 ) R_4(\theta_4) R4(θ4)、 R 5 ( θ 5 ) R_5(\theta_5) R5(θ5)、 R 6 ( θ 6 ) R_6(\theta_6) R6(θ6)表示各轴的变换矩阵。将对关节轴4、5、6的旋转看成是动欧拉角ZYZ的旋转模式,其旋转矩阵为 R ( θ 4 , θ 5 , θ 6 ) R(\theta_4,\theta_5,\theta_6) R(θ4,θ5,θ6)。
R ( θ 4 , θ 5 , θ 6 ) = [ c o s θ 4 − s i n θ 4 0 s i n θ 4 c o s θ 4 0 0 0 1 ] [ c o s θ 5 0 s i n θ 5 0 1 0 − s i n θ 5 0 c o s θ 5 ] [ c o s θ 6 − s i n θ 6 0 s i n θ 6 c o s θ 6 0 0 0 1 ] (3) R(\theta_4,\theta_5,\theta_6) = \begin{bmatrix} cos\theta_4&-sin\theta_4&0\\ sin\theta_4&cos\theta_4&0\\ 0&0&1\\ \end{bmatrix} \begin{bmatrix} cos\theta_5&0&sin\theta_5\\ 0&1&0\\ -sin\theta_5&0&cos\theta_5\\ \end{bmatrix} \begin{bmatrix} cos\theta_6&-sin\theta_6&0\\ sin\theta_6&cos\theta_6&0\\ 0&0&1\\ \end{bmatrix} \tag3 R(θ4,θ5,θ6)= cosθ4sinθ40−sinθ4cosθ40001 cosθ50−sinθ5010sinθ50cosθ5 cosθ6sinθ60−sinθ6cosθ60001 (3)
具体计算得:
R ( θ 4 , θ 5 , θ 6 ) = [ c o s θ 4 c o s θ 5 c o s θ 6 − s i n θ 4 s i n θ 6 − c o s θ 4 c o s θ 5 s i n θ 6 − s i n θ 4 c o s c o s θ 6 θ 4 s i n θ 5 s i n θ 4 c o s θ 5 c o s θ 6 + c o s θ 4 s i n θ 6 − s i n θ 4 c o s θ 5 s i n θ 6 + c o s θ 4 c o s θ 6 s i n θ 4 s i n θ 5 − s i n θ 5 c o s θ 6 s i n θ 5 s i n θ 6 c o s θ 5 ] (4) R(\theta_4,\theta_5,\theta_6) = \begin{bmatrix} cos\theta_4cos\theta_5cos\theta_6-sin\theta_4sin\theta_6&-cos\theta_4cos\theta_5sin\theta_6-sin\theta_4cos&cos\theta_6\theta_4sin\theta_5\\ sin\theta_4cos\theta_5cos\theta_6+cos\theta_4sin\theta_6&-sin\theta_4cos\theta_5sin\theta_6+cos\theta_4cos\theta_6&sin\theta_4sin\theta_5\\ -sin\theta_5cos\theta_6&sin\theta_5sin\theta_6&cos\theta_5\\ \end{bmatrix} \tag4 R(θ4,θ5,θ6)= cosθ4cosθ5cosθ6−sinθ4sinθ6sinθ4cosθ5cosθ6+cosθ4sinθ6−sinθ5cosθ6−cosθ4cosθ5sinθ6−sinθ4cos−sinθ4cosθ5sinθ6+cosθ4cosθ6sinθ5sinθ6cosθ6θ4sinθ5sinθ4sinθ5cosθ5 (4)
由机械臂的正运动学可得:
R ( θ 1 ) R ( θ 2 ) R ( θ 3 ) R ( θ 4 = 0 ) R ( θ 4 , θ 5 , θ 6 ) = R P (5) R(\theta_1)R(\theta_2)R(\theta_3)R(\theta_4=0)R(\theta_4, \theta_5, \theta_6)=R_P \tag5 R(θ1)R(θ2)R(θ3)R(θ4=0)R(θ4,θ5,θ6)=RP(5)
在公式(5)中, R P R_P RP为机械臂末端点 P P P的姿态。对公式(5)进行移项得:
R ( θ 4 , θ 5 , θ 6 ) = [ R ( θ 1 ) R ( θ 2 ) R ( θ 3 ) R ( θ 4 = 0 ) ] − 1 R P = [ r 11 r 12 r 13 r 21 r 22 r 23 r 31 r 32 r 33 ] (6) R(\theta_4, \theta_5, \theta_6)=[R(\theta_1)R(\theta_2)R(\theta_3)R(\theta_4=0)]^{-1}R_P= \begin{bmatrix} r_{11}&r_{12}&r_{13}\\ r_{21}&r_{22}&r_{23}\\ r_{31}&r_{32}&r_{33}\\ \end{bmatrix} \tag6 R(θ4,θ5,θ6)=[R(θ1)R(θ2)R(θ3)R(θ4=0)]−1RP= r11r21r31r12r22r32r13r23r33 (6)
联立公式(4)(6)可得两组解:
{ θ 4 = a t a n 2 ( r 23 , r 13 ) θ 5 = a t a n 2 ( s q r t ( r 31 2 + r 32 2 ) , r 33 ) θ 6 = a t a n 2 ( r 32 , − r 31 ) (7) \begin{cases} \theta_4=atan2(r_{23}, r_{13})\\ \theta_5=atan2(sqrt(r_{31}^2+r_{32}^2), r_{33})\\ \theta_6=atan2(r_{32}, -r_{31}) \end{cases} \tag7 ⎩ ⎨ ⎧θ4=atan2(r23,r13)θ5=atan2(sqrt(r312+r322),r33)θ6=atan2(r32,−r31)(7)
{ θ 4 = a t a n 2 ( r 23 , r 13 ) + π θ 5 = − a t a n 2 ( s q r t ( r 31 2 + r 32 2 ) , r 33 ) θ 6 = a t a n 2 ( r 32 , − r 31 ) + π (8) \begin{cases} \theta_4=atan2(r_{23}, r_{13}) + \pi\\ \theta_5=-atan2(sqrt(r_{31}^2+r_{32}^2), r_{33})\\ \theta_6=atan2(r_{32}, -r_{31}) + \pi \end{cases} \tag8 ⎩ ⎨ ⎧θ4=atan2(r23,r13)+πθ5=−atan2(sqrt(r312+r322),r33)θ6=atan2(r32,−r31)+π(8)
综上,完成机械臂的运动学逆解的解析解求解过程,可能存在8个以上的解,可根据一些约束调节对求得的解进行删选,如关节限位、碰撞检测等。
示例程序
import numpy as np
import math
from pyquaternion import Quaternionnp.set_printoptions(suppress=True)# DH矩阵每列的含义:连杆夹角、连杆长度、连杆偏距、初始关节角
DH = np.mat([[ 0, 0, 0.1, 0], [ 0.5 * math.pi, 0, 0, 0], [ 0, 0.5, 0, 0.5 * math.pi], [ 0.5 * math.pi, 0, 0.5, 0], [-0.5 * math.pi, 0, 0, 0], [ 0.5 * math.pi, 0, 0, 0]])def transformToMatrix(alpha, a, d, theta):T0 = np.eye(4)T1 = np.mat([[1, 0, 0, 0], [0, math.cos(alpha), -math.sin(alpha), 0], [0, math.sin(alpha), math.cos(alpha), 0], [0, 0, 0, 1]])T2 = np.mat([[1, 0, 0, a], [0, 1, 0, 0], [0, 0, 1, d], [0, 0, 0, 1]])T3 = np.mat([[math.cos(theta), -math.sin(theta), 0, 0], [math.sin(theta), math.cos(theta), 0, 0], [ 0, 0, 1, 0], [ 0, 0, 0, 1]])return T1 * T2 * T3def forwardKinematic(DH, j0, j1, j2, j3, j4, j5):T0 = transformToMatrix(DH[0, 0], DH[0, 1], DH[0, 2], DH[0, 3] + j0)T1 = transformToMatrix(DH[1, 0], DH[1, 1], DH[1, 2], DH[1, 3] + j1)T2 = transformToMatrix(DH[2, 0], DH[2, 1], DH[2, 2], DH[2, 3] + j2)T3 = transformToMatrix(DH[3, 0], DH[3, 1], DH[3, 2], DH[3, 3] + j3)T4 = transformToMatrix(DH[4, 0], DH[4, 1], DH[4, 2], DH[4, 3] + j4)T5 = transformToMatrix(DH[5, 0], DH[5, 1], DH[5, 2], DH[5, 3] + j5)#print(T0 * T1 * T2 * T3 * T4 * T5)return T0 * T1 * T2 * T3 * T4 * T5def calcu3ForwardJointAngle(DH, j0, x0, y0, x, y, b, js):if abs((x0 - x) * (x0 - x) + (y0 - y) * (y0 - y) - b*b) < 0.0001:js.append([j0])js[-1].append(math.atan2(y0, x0))js[-1].append(math.atan2(y - y0, x - x0) - math.atan2(y0, x0) + 0.5 * math.pi - DH[2, 3])js.append([j0 + math.pi])js[-1].append(math.pi - math.atan2(y0, x0))js[-1].append(math.atan2(y0, x0) - math.atan2(y - y0, x - x0) + 0.5 * math.pi - DH[2, 3])if abs((x0 - x) * (x0 - x) + (-y0 - y) * (-y0 - y) - b*b) < 0.0001:js.append([j0])js[-1].append(math.atan2(-y0, x0))js[-1].append(math.atan2(y + y0, x - x0) - math.atan2(-y0, x0) + 0.5 * math.pi - DH[2, 3])js.append([j0 + math.pi])js[-1].append(math.pi - math.atan2(-y0, x0))js[-1].append(math.atan2(-y0, x0) - math.atan2(y + y0, x - x0) + 0.5 * math.pi - DH[2, 3])def quaternionToRotationMatrix(x, y, z, w):# a = math.sqrt(x*x + y*y + z*z)# if a == 0:# return np.eye(3)# v1x = 0# v1y = -z# v1z = y# b = math.sqrt(v1x*v1x + v1y*v1y + v1z*v1z)# if b == 0:# v1y = 1.0# v1z = 0.0# b = 1.0# v2 = np.cross(np.array([x, y, z]), np.array([v1x, v1y, v1z]))# #print(np.array([x, y, z]), np.array([v1x, v1y, v1z]), v2)# c = math.sqrt(v2[0]*v2[0] + v2[1]*v2[1] + v2[2]*v2[2])# R01 = np.mat([[x / a, v1x / b, v2[0] / c],# [y / a, v1y / b, v2[1] / c],# [z / a, v1z / b, v2[2] / c]])# theta = 2 * math.acos(w)# #print(R01)# R12 = np.mat([[1, 0, 0],# [0, math.cos(theta), -math.sin(theta)],# [0, math.sin(theta), math.cos(theta)]])# return R01 * R12 * np.linalg.inv(R01)a = math.sqrt(x*x + y*y + z*z + w*w)if a == 0:print('quaternion is error')return np.eye(3)x = x / ay = y / az = z / aw = w / areturn np.mat([[1 - 2*y*y - 2*z*z, 2*x*y - 2*z*w, 2*x*z + 2*y*w],[ 2*x*y + 2*z*w, 1 - 2*x*x - 2*z*z, 2*y*z - 2*x*w],[ 2*x*z - 2*y*w, 2*y*z + 2*x*w, 1 - 2*x*x - 2*y*y]])def rotateMatrixToQuaternion(R):R1 = [[R[0, 0], R[0, 1], R[0, 2]],[R[1, 0], R[1, 1], R[1, 2]],[R[2, 0], R[2, 1], R[2, 2]]]q = Quaternion(matrix=np.array(R1))return q.x, q.y, q.z, q.wdef inverseKinematic(DH, x, y, z, ox, oy, oz, ow):q_length = math.sqrt(ox*ox + oy*oy + oz*oz + ow*ow)if q_length == 0:print('quaternion is error')returnelse:ox = ox / q_lengthoy = oy / q_lengthoz = oz / q_lengthow = ow / q_lengthjs = []j00 = math.atan2(y, x)a = DH[2, 1]b = DH[3, 2]c = math.sqrt(x*x + y*y + (z - DH[0, 2])*(z - DH[0, 2]))a0 = 4*(x*x+y*y) + 4*(z - DH[0, 2])*(z - DH[0, 2])a1 = -4*(a*a - b*b + c*c)*math.sqrt(x*x + y*y)a2 = (a*a - b*b + c*c) * (a*a - b*b + c*c) - 4 * (z - DH[0, 2]) * (z - DH[0, 2]) * a * aif a1*a1 - 4*a0*a2 > 0:x0 = (-a1 + math.sqrt(a1*a1 - 4*a0*a2)) / (2 * a0)y0 = math.sqrt(a*a - x0*x0)#print('x0: ', x0, 'y0: ', y0)calcu3ForwardJointAngle(DH, j00, x0, y0, math.sqrt(x*x+y*y), z - DH[0, 2], b, js)x0 = (-a1 - math.sqrt(a1*a1 - 4*a0*a2)) / (2 * a0)y0 = math.sqrt(a*a - x0*x0)#print('x1: ', x0, 'y1: ', y0)calcu3ForwardJointAngle(DH, j00, x0, y0, math.sqrt(x*x+y*y), z - DH[0, 2], b, js)elif a1*a1 - 4*a0*a2 == 0:x0 = (-a1) / (2 * a0)y0 = math.sqrt(a*a - x0*x0)#print('x0: ', x0, 'y0: ', y0)calcu3ForwardJointAngle(DH, j00, x0, y0, math.sqrt(x*x+y*y), z - DH[0, 2], b, js)else:print('no solve')js = [[]]new_js = []for j in js:R = quaternionToRotationMatrix(ox, oy, oz, ow)T01 = transformToMatrix(DH[0, 0], DH[0, 1], DH[0, 2], DH[0, 3] + j[0])T12 = transformToMatrix(DH[1, 0], DH[1, 1], DH[1, 2], DH[1, 3] + j[1])T23 = transformToMatrix(DH[2, 0], DH[2, 1], DH[2, 2], DH[2, 3] + j[2])T34 = transformToMatrix(DH[3, 0], DH[3, 1], DH[3, 2], DH[3, 3])R01 = np.mat([[T01[0, 0], T01[0, 1], T01[0, 2]],[T01[1, 0], T01[1, 1], T01[1, 2]],[T01[2, 0], T01[2, 1], T01[2, 2]]])R12 = np.mat([[T12[0, 0], T12[0, 1], T12[0, 2]],[T12[1, 0], T12[1, 1], T12[1, 2]],[T12[2, 0], T12[2, 1], T12[2, 2]]])R23 = np.mat([[T23[0, 0], T23[0, 1], T23[0, 2]],[T23[1, 0], T23[1, 1], T23[1, 2]],[T23[2, 0], T23[2, 1], T23[2, 2]]])R34 = np.mat([[T34[0, 0], T34[0, 1], T34[0, 2]],[T34[1, 0], T34[1, 1], T34[1, 2]],[T34[2, 0], T34[2, 1], T34[2, 2]]])R = (R34.T) * (R23.T) * (R12.T) * (R01.T) * R#print('RRRRRRRRR: \n', R)alpha = math.atan2(R[1, 2], R[0, 2])betla = math.atan2(math.sqrt(R[2, 0]*R[2, 0] + R[2, 1]*R[2, 1]), R[2, 2])gamal = math.atan2(R[2, 1], -R[2, 0])new_js.append([])new_js[-1].append(j[0])new_js[-1].append(j[1])new_js[-1].append(j[2])new_js[-1].append(alpha)new_js[-1].append(betla)new_js[-1].append(gamal)#print(new_js[-1])new_js.append([])new_js[-1].append(j[0])new_js[-1].append(j[1])new_js[-1].append(j[2])new_js[-1].append(alpha + math.pi)new_js[-1].append(-betla)new_js[-1].append(gamal + math.pi)#print(new_js[-1])return new_jsif __name__ == '__main__':print("hello world")#print(DH)print(forwardKinematic(DH, 1, 0, 0, 0, 0, 0))js = inverseKinematic(DH, 0.5, 0.11, 0.26, 0.0, 0.0, 0.8, 0.6)print('##########################')for j in js:print('joint angle: ', j)T = forwardKinematic(DH, j[0], j[1], j[2], j[3], j[4], j[5])#print('P: ', T[0, 3], T[1, 3], T[2, 3])#print('Q: ', rotateMatrixToQuaternion(T))print('##########################')
注意实现
- 此运动学逆解求解器不具备通用性,只适用于满足以上DH矩阵格式的6轴串联机器人;
- 示例程序中,没有对所求的解进行筛选,存在超出限位、碰撞的情况;
- 在求解2元2次方程组时,注意其中的非实数解;
相关文章:

工业6轴机械臂运动学逆解(解析解)
工业6轴机械臂运动学逆解(解析解) 通常工业机械臂采用6旋转轴串连的形式,保证了灵活性,但为其运动学逆解(即已知机械臂末端的位姿 P P P,求机械臂各个旋转轴的旋转角)带来了较大的困难ÿ…...

管理类联考——数学——真题篇——按题型分类——充分性判断题——蒙猜A/B
老规矩,看目录,平均3-5题 文章目录 A/B2023真题(2023-19)-A-选项特点:两个等号;-判断需联立的难易:难,看着感觉需要联立,所以判断联立需要有理论支撑,不然还…...
为什么GRU和LSTM能够缓解梯度消失或梯度爆炸问题?
1、什么是梯度消失(gradient vanishing)? 参数更新过小,在每次更新时几乎不会移动,导致模型无法学习。 2、什么是梯度爆炸(gradient exploding)? 参数更新过小大,破坏了…...

【力扣100】146.LRU缓存
添加链接描述 class DLinkedNode:def __init__(self, key0, value0):self.key keyself.value valueself.prev Noneself.next Noneclass LRUCache:def __init__(self, capacity: int):self.cache dict()# 使用伪头部和伪尾部节点 self.head DLinkedNode()self.tail D…...
【Vue中给输入框加入js验证_blur失去焦点进行校验】
【Vue中给输入框加入js验证_blur失去焦点进行校验】 通俗一点就是给输入框加个光标离开当前文本输入框时,然后对当前文本框内容进行校验判断 具体如下: 1.先给文本框加属性 blur“validatePhoneNumber” <el-input v-model“entity.telephone” blur…...

vue3项目引入电子签名(可横屏竖屏)
实现效果:(左边横屏,右边竖屏) 前言:【使用开源项目smooth-signature 实现签名的功能。Gitee 地址是 :GitHub - linjc/smooth-signature: H5带笔锋手写签名,支持PC端和移动端,任何前…...
、count(1)、count(主键)、count(字段)的区别)
mysql中count(*)、count(1)、count(主键)、count(字段)的区别
文章目录 count函数的语义count(主键)count(1)count(*)count(字段)替代方案explain或者show table status中间表或者其他数据库计数 以下分析都是基于 select count(?) from table 这个语句来分析,不带过滤条件。 count函数的语义 count() 是一个聚合函数&#x…...

Nginx生成自签名证书从而添加域名的HTTPS访问
数字证书 ## 原理参考 https://mysticaldream.github.io/2023/05/certificate/## https://blog.csdn.net/m0_52440465/article/details/130713591 简介 数字证书是由证书颁发机构(CA)签名并颁发的电子文件,用于建立网络连接的身份认证和加密通信。SSL 证书是数字证书的一种。…...

无框架Java转go语言写http与tcp请求
项目地址 https://github.com/cmdch2017/http_tcpServer 项目结构 如何快速上手 http篇 1、controller包就相当于RestController,这里返回了一个Person对象,当你需要新建一个接口时,再新写一个func仿照下面的方法就行了 package control…...
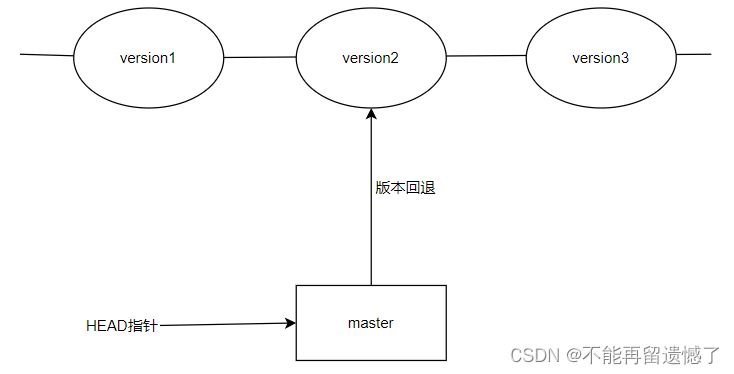
【Git】Git基本操作
文章目录 Git 是什么Git 的优点Git 安装Linux UbuntuLinux CentOsWindows Git 基本操作1. 创建 Git 本地仓库2. 配置 Git3. Git工作区、暂存区和版本库4. 添加文件5. 查看 .git 文件6. 修改文件7. 版本回退 Git 是什么 Git是一个免费的、开源的分布式版本控制系统,…...

JavaSE学习笔记 Day20
JavaSE学习笔记 Day20 个人整理非商业用途,欢迎探讨与指正!! 上一篇 文章目录 JavaSE学习笔记 Day20十七、数据结构与算法17.1算法17.1.1冒泡排序17.1.2选择排序17.1.3插入排序17.1.4三个排序的区别 17.2顺序表17.2.1顺序表代码实现17.2.2顺…...

【蓝桥杯选拔赛真题52】python空调模式 第十四届青少年组蓝桥杯python 选拔赛比赛真题解析
目录 python空调模式 一、题目要求 1、编程实现 2、输入输出...
Android Studio: 解决Gradle sync failed 错误
文章目录 1. 前言2. 错误情况3. 解决办法3.1 获取gradle下载地址3.2 获取gradle存放目录3.3 替换并删除临时文件3.4 触发Try Again 4. 执行成功 1. 前言 今天调试项目,发现新装的AS,在下载gradle的过程中,一直显示连接失败,Gradl…...

【手写数据库】从零开始手写数据库内核,行列混合存储模型,学习大纲成型了
目录 专栏内容: 参天引擎内核架构 本专栏一起来聊聊参天引擎内核架构,以及如何实现多机的数据库节点的多读多写,与传统主备,MPP的区别,技术难点的分析,数据元数据同步,多主节点的情况下对故障容灾的支持。 手写数据库toadb 本专栏主要介绍如何从零开发,开发的步骤,以…...
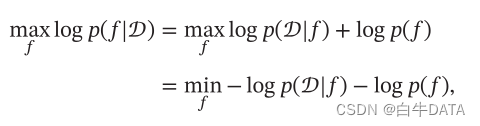
机器学习中的一些经典理论定理
PAC学习理论 当使用机器学习方法来解决某个特定问题时,通常靠经验或者多次试验来选择合适的模型、训练样本数量以及学习算法收敛的速度等。但是经验判断或多次试验往往成本比较高,也不太可靠,因此希望有一套理论能够分析问题难度、计算模型能…...
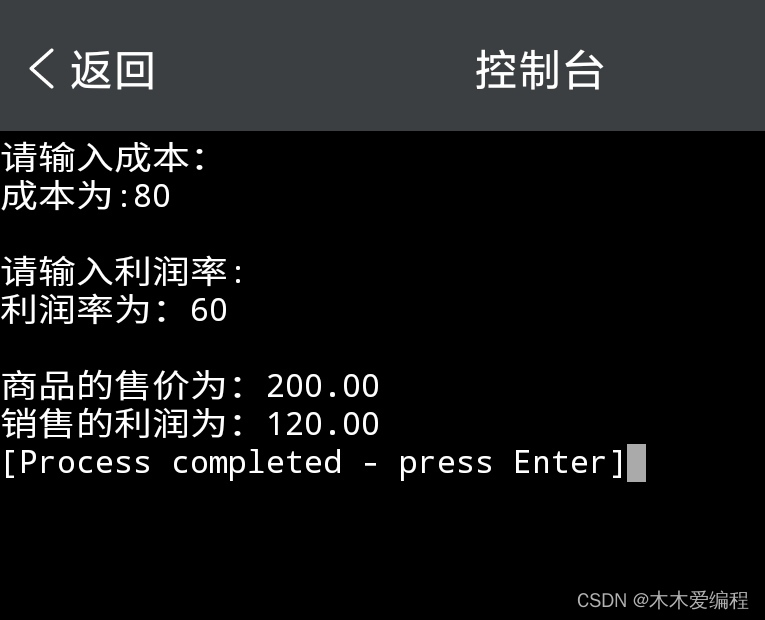
c语言:成本100元,40%的利润怎么计算|练习题
一、利润的计算公式: 利润售价-成本 售价成本/(1-利润率) 二、用c语言代码表示为: 如图: 三、计算源代码【带注释】 #include <stdio.h> int main() { float cost;//成本变量 int prof_rate;//利润率变量 float price;//…...

【Python必做100题】之第二十二题(复制列表)
题目:将一个列表的数据复制到另一个列表中 重点:确保复制到位要导入copy方法进行深度复制 代码如下: #将一个列表的数据复制到另一个列表中 import copy list [1,2,3,4] print(list) list1 copy.copy(list) list[0] 30 print(list) pri…...
Java 数据结构篇-实现堆的核心方法与堆的应用(实现 TOP-K 问题:最小 k 个数)
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 文章目录 1.0 堆的说明 2.0 堆的成员变量及其构造方法 3.0 实现堆的核心方法 3.1 实现堆的核心方法 - 获取堆顶元素 peek() 3.2 实现堆的核心方法 - 下潜 down(int i) 3.3 实…...

startUML6.0.1破解方法
startUML6.0.1破解方法 文章目录 startUML6.0.1破解方法1.startUML6.0.1快速破解2.概述3.安装Nodejs4.安装asar5.修改app.asar中的源码6.将修改后的源码重新压缩7.覆盖官方的asar文件8.重启startUML9.参考文档 1.startUML6.0.1快速破解 后绪步骤可以不看,直接下载我…...

Python实现多种图像分割方法:基于阈值分割和基于区域分割
Python实现多种图像分割方法:基于阈值分割和基于区域分割 图像分割是图像分析的第一步,是计算机视觉的基础,但也是图像处理中最困难的问题之一。经典的计算机视觉任务,如目标检测、图像识别等都和图像分割相关,图像分…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...
