1.1 数据结构-数据的表示
文章目录
- 1.1.1 二元关系及其性质:
- 1.1.1.1 笛卡尔积:
- 1.1.1.2 二元关系:
- 持续更新当中 .......
1.1.1 二元关系及其性质:
数据的基本单元称为额数据元素,数据是从客观事物的观测中的到的,数据元素并不是鼓励存在的,而是存在密切的联系,也因此才能表示和描述客观事物,数据元素之间的联系,归纳起来有三种,即一对一,一对多的联系,和多对多的联系. 无论哪一种联系.都可以借助于二元关系进行描述;因此"二元关系"是描述数据元素关系的基础.
二元关系是一个数学概念,他定义在集合的基本运算-----笛卡尔积(英文叫Cartesian product)的基础上.因此下面将从集合的笛卡尔积的定义来出发,来解释二元关系的概念及其性质。
1.1.1.1 笛卡尔积:
对于两个集合可以定义一种成绩运算,即集合的笛卡尔积.
比如集合只有M和N,分别表示为M={x},N={y} ,则集合M和N的笛卡尔积,记作:M X N,定义为:
M x N = { (x,y) | x ∈ M 且 y ∈ N}
也就是说,两个集合M和N的笛卡尔积也是一个集合,这个集合 M x N 中的每个元素都是一个二元组,称为有序或者序偶. 有序对的地一个元素来自第一个集合M,有序对的集合的第二元素来自于第二个集合N. 笛卡尔积M x N将取遍集合M和N中所有的元素组合,如果集合M中的元素个数为m,集合N的元素个数是n那么M x N中的元素个数为 m x n
例如: M = (a1,a2) ,N = (0,1,2) 则 :
M x N = {(a1,0),(a1,2),(a1,2),(a2,0),(a2,2),(a2,2)}
笛卡尔积的元素是有序对,因此集合的笛卡尔积是不可交换的,即:
M x N ≠ N x M
1.1.1.2 二元关系:
有了集合的笛卡尔积,就可以进一步讨论二元关系,
定义:设有集合M,N ,其笛卡尔积 M x N 的任意一个子集 R ∈ M x N ,被称为 M到N的一个二元关系.
二元关系表示了集合M和集合N中元素之间的某种相关性.若有序对 (a,b) ∈ R ,也可以记作 aRb,则称a是b的关于R的前件,或者说直接前驱;b是a关于R的后件或者说直接后继.
举例:
我们假如有一个学生学习语文,数学和英文,表示为 M = {语文,数学,英语}
那我们设定成绩为四个等级 ,记作 N = {A,B,C,D}
这个学生成绩的全部可能为:
{ (语文, A),(语文, B),(语文, C),(语文, D),(数学, A),(数学, B),(数学, C),(数学, D),(英语, A),(英语, B),(英语, C),(英语, D)}
如果这个学生的实际成绩R = {(语文, B),(数学, A),(英语, D)}那么我们看到的R是笛卡尔积 MxN的一个子集, 因此R是M到N的一个二元关系,他表示了这个学生的功课和成绩的对应关系;
二元关系是普遍存在的,例如实数域上相等关系 = ,小于等于关系 ,平面上的三角形的全等三角形关系.生活中父子关系,同班同学关系等
- 相等关系(=): 在实数域上,相等关系是一个二元关系,表示两个数在数值上相等。例如,3=33=3 表示 3 等于 3。
- 小于等于关系(≤): 这是实数域上的另一个二元关系,表示一个数小于或等于另一个数。例如,2≤52≤5 表示 2 小于或等于 5。
- 全等关系: 在平面几何中,全等关系表示两个三角形或其他几何形状在形状和大小上完全相同。这是一种二元关系,通常使用符号 ≅≅ 表示。例如,如果两个三角形的对应边和对应角相等,则它们是全等的。
- 父子关系: 在家庭结构中,父子关系是一个二元关系,表示父母和子女之间的连接。如果 A 是 B 的父母,我们可以表示为 (A,B) 属于父子关系。
- 同学关系: 在学校环境中,同学关系表示两个学生在同一个班级中学习。如果 A 和 B 是同班同学,我们可以表示为(A,B) 属于同学关系。
持续更新当中 …
相关文章:

1.1 数据结构-数据的表示
文章目录 1.1.1 二元关系及其性质:1.1.1.1 笛卡尔积:1.1.1.2 二元关系:持续更新当中 ....... 1.1.1 二元关系及其性质: 数据的基本单元称为额数据元素,数据是从客观事物的观测中的到的,数据元素并不是鼓励存在的,而是存在密切的联系,也因此才能表示和描述客观事物,数据元素之间…...
])
UNIX Linux系统 启动PPOCRLabel报错[已放弃 (核心已转储)]
参照官方教程安装后,启动PPOCRLabel报错:[已放弃 (核心已转储)] 官方链接地址:PPOCRLabelv2 $~ PPOCRLabel --lang ch QObject::moveToThread: Current thread (0x561534309430) is not the objects thread (0x56153929eac0). Cannot move to…...

前端开发中的webpack打包工具
前端技术发展迅猛,各种可以提高开发效率的新思想和框架层出不穷,但是它们都有一个共同点,即源代码无法直接运行,必须通过转换后才可以正常运行。webpack是目前主流的打包模块化JavaScript的工具之一。 本章主要涉及的知识点有&am…...
)
Mybatis配置-数据库厂商标识(databaseIdProvider)
MyBatis可以根据数据库供应商执行不同的语句。多数据库供应商支持是基于映射语句的databaseId属性。MyBatis将加载所有没有databaseId属性或具有与当前数据库匹配的databaseId属性的语句。如果找到具有和不具有databaseId的相同语句,则后者将被丢弃。要启用多供应商…...

【Java】使用递归的方法获取层级关系数据demo
使用递归来完善各种业务数据的层级关系的获取 引言:在Java开发中,我们通常会遇到层层递进的关系型数据的获取问题,有时是树状解构,或金字塔结构,怎么描述都行,错综复杂的关系在程序中还是可以理清的。 这…...
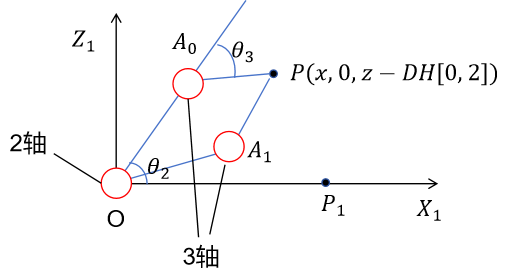
工业6轴机械臂运动学逆解(解析解)
工业6轴机械臂运动学逆解(解析解) 通常工业机械臂采用6旋转轴串连的形式,保证了灵活性,但为其运动学逆解(即已知机械臂末端的位姿 P P P,求机械臂各个旋转轴的旋转角)带来了较大的困难ÿ…...

管理类联考——数学——真题篇——按题型分类——充分性判断题——蒙猜A/B
老规矩,看目录,平均3-5题 文章目录 A/B2023真题(2023-19)-A-选项特点:两个等号;-判断需联立的难易:难,看着感觉需要联立,所以判断联立需要有理论支撑,不然还…...
为什么GRU和LSTM能够缓解梯度消失或梯度爆炸问题?
1、什么是梯度消失(gradient vanishing)? 参数更新过小,在每次更新时几乎不会移动,导致模型无法学习。 2、什么是梯度爆炸(gradient exploding)? 参数更新过小大,破坏了…...

【力扣100】146.LRU缓存
添加链接描述 class DLinkedNode:def __init__(self, key0, value0):self.key keyself.value valueself.prev Noneself.next Noneclass LRUCache:def __init__(self, capacity: int):self.cache dict()# 使用伪头部和伪尾部节点 self.head DLinkedNode()self.tail D…...
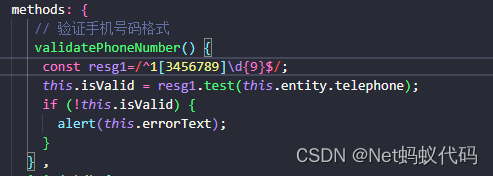
【Vue中给输入框加入js验证_blur失去焦点进行校验】
【Vue中给输入框加入js验证_blur失去焦点进行校验】 通俗一点就是给输入框加个光标离开当前文本输入框时,然后对当前文本框内容进行校验判断 具体如下: 1.先给文本框加属性 blur“validatePhoneNumber” <el-input v-model“entity.telephone” blur…...

vue3项目引入电子签名(可横屏竖屏)
实现效果:(左边横屏,右边竖屏) 前言:【使用开源项目smooth-signature 实现签名的功能。Gitee 地址是 :GitHub - linjc/smooth-signature: H5带笔锋手写签名,支持PC端和移动端,任何前…...
、count(1)、count(主键)、count(字段)的区别)
mysql中count(*)、count(1)、count(主键)、count(字段)的区别
文章目录 count函数的语义count(主键)count(1)count(*)count(字段)替代方案explain或者show table status中间表或者其他数据库计数 以下分析都是基于 select count(?) from table 这个语句来分析,不带过滤条件。 count函数的语义 count() 是一个聚合函数&#x…...

Nginx生成自签名证书从而添加域名的HTTPS访问
数字证书 ## 原理参考 https://mysticaldream.github.io/2023/05/certificate/## https://blog.csdn.net/m0_52440465/article/details/130713591 简介 数字证书是由证书颁发机构(CA)签名并颁发的电子文件,用于建立网络连接的身份认证和加密通信。SSL 证书是数字证书的一种。…...

无框架Java转go语言写http与tcp请求
项目地址 https://github.com/cmdch2017/http_tcpServer 项目结构 如何快速上手 http篇 1、controller包就相当于RestController,这里返回了一个Person对象,当你需要新建一个接口时,再新写一个func仿照下面的方法就行了 package control…...
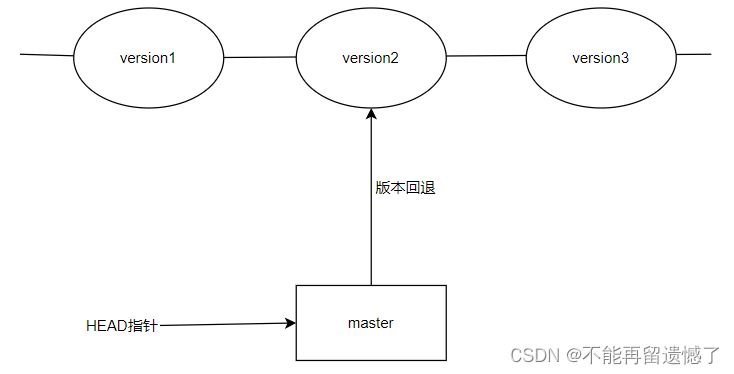
【Git】Git基本操作
文章目录 Git 是什么Git 的优点Git 安装Linux UbuntuLinux CentOsWindows Git 基本操作1. 创建 Git 本地仓库2. 配置 Git3. Git工作区、暂存区和版本库4. 添加文件5. 查看 .git 文件6. 修改文件7. 版本回退 Git 是什么 Git是一个免费的、开源的分布式版本控制系统,…...

JavaSE学习笔记 Day20
JavaSE学习笔记 Day20 个人整理非商业用途,欢迎探讨与指正!! 上一篇 文章目录 JavaSE学习笔记 Day20十七、数据结构与算法17.1算法17.1.1冒泡排序17.1.2选择排序17.1.3插入排序17.1.4三个排序的区别 17.2顺序表17.2.1顺序表代码实现17.2.2顺…...

【蓝桥杯选拔赛真题52】python空调模式 第十四届青少年组蓝桥杯python 选拔赛比赛真题解析
目录 python空调模式 一、题目要求 1、编程实现 2、输入输出...
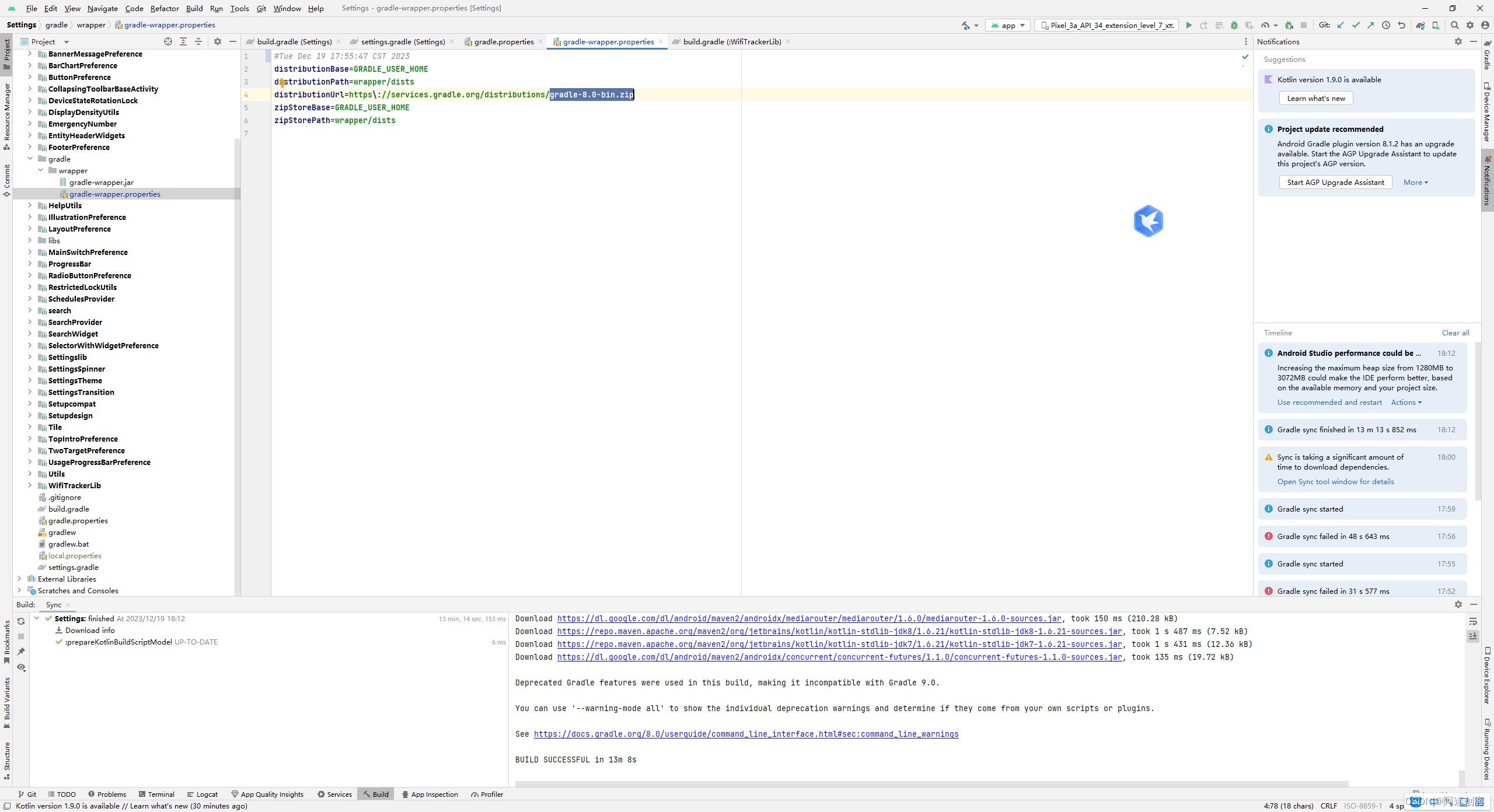
Android Studio: 解决Gradle sync failed 错误
文章目录 1. 前言2. 错误情况3. 解决办法3.1 获取gradle下载地址3.2 获取gradle存放目录3.3 替换并删除临时文件3.4 触发Try Again 4. 执行成功 1. 前言 今天调试项目,发现新装的AS,在下载gradle的过程中,一直显示连接失败,Gradl…...

【手写数据库】从零开始手写数据库内核,行列混合存储模型,学习大纲成型了
目录 专栏内容: 参天引擎内核架构 本专栏一起来聊聊参天引擎内核架构,以及如何实现多机的数据库节点的多读多写,与传统主备,MPP的区别,技术难点的分析,数据元数据同步,多主节点的情况下对故障容灾的支持。 手写数据库toadb 本专栏主要介绍如何从零开发,开发的步骤,以…...
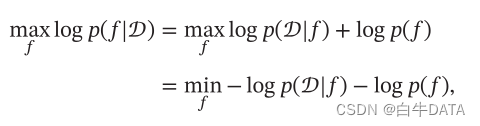
机器学习中的一些经典理论定理
PAC学习理论 当使用机器学习方法来解决某个特定问题时,通常靠经验或者多次试验来选择合适的模型、训练样本数量以及学习算法收敛的速度等。但是经验判断或多次试验往往成本比较高,也不太可靠,因此希望有一套理论能够分析问题难度、计算模型能…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...
