2023-12-20 二叉搜索树的最近公共祖先和二叉搜索树中的插入操作和删除二叉搜索树中的节点
235. 二叉搜索树的最近公共祖先
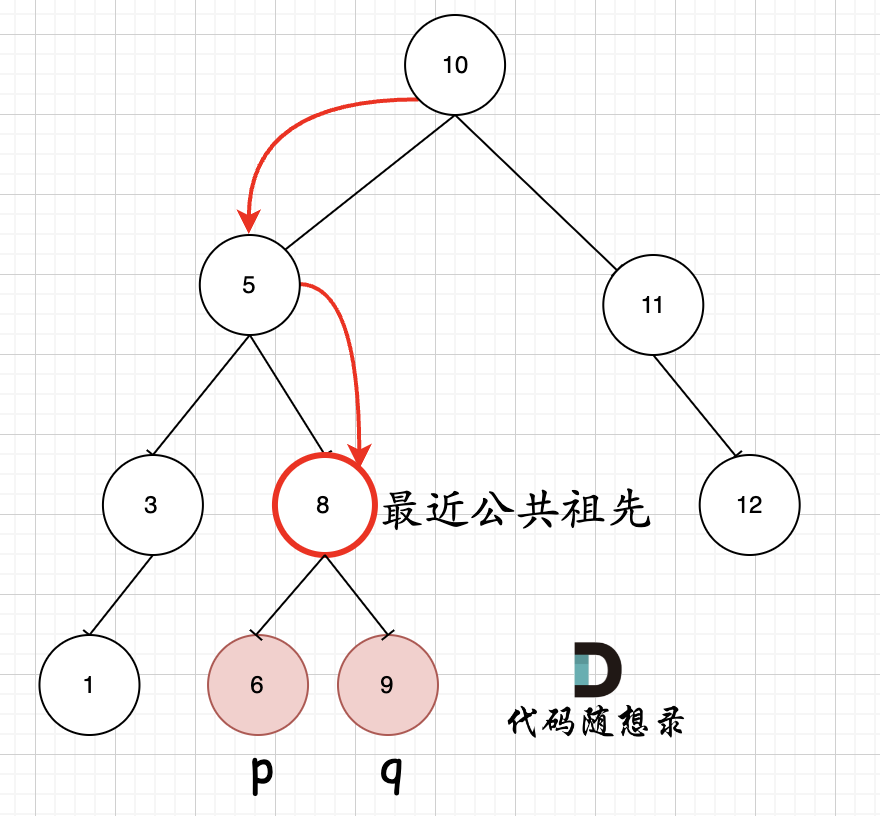
思想:和二叉树的公共最近祖先节点的思路基本一致的!就是不用从下往上遍历处理!可以利用的二叉搜索树的特点从上往下处理了!而且最近公共节点肯定是第一个出现在【q,p】这个区间的内的!
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = Noneclass Solution:def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':return self.lowestCommonAncestor1(root, p, q)def lowestCommonAncestor1(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':# 二叉搜索树,是有序的,不同于二叉树的公共祖先需要从下往上遍历# 而且公共节点一定会出现在【p,q】之前,我们递归遍历,最先出现在这个区间就是公共祖先节点了if root is None:return root# 处理中节点了if root.val > q.val and root.val > p.val: # 处理左节点left = self.lowestCommonAncestor(root.left, p, q)if left is not None:# if not left: 这种用来判断节点不对的!return leftif root.val < q.val and root.val < p.val:right = self.lowestCommonAncestor(root.right, p, q)if right is not None:return rightreturn root
701. 二叉搜索树中的插入操作
思路:只要按照二叉搜索树的规则去遍历,遇到空节点就插入节点就可以了!通过递归函数返回值完成了新加入节点的父子关系赋值操作了,下一层将加入节点返回,本层用root->left或者root->right将其接住
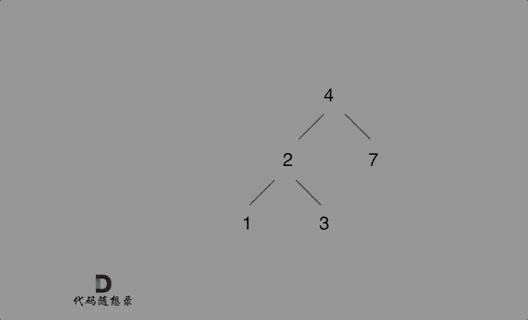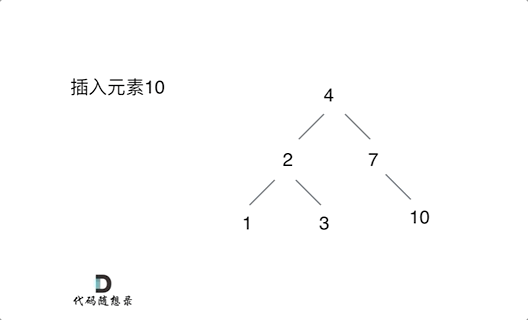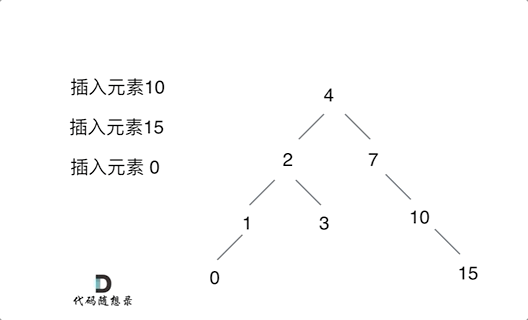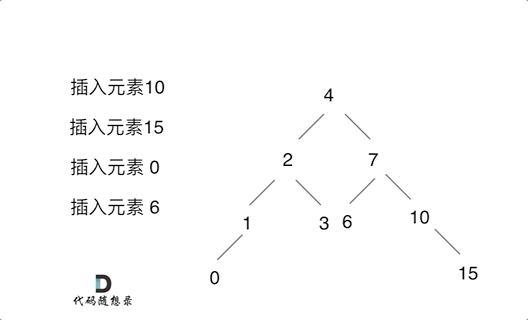
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:if root is None:node = TreeNode(val)# root = nodereturn nodeif root.val > val:root.left = self.insertIntoBST(root.left, val) # 左if root.val < val:root.right = self.insertIntoBST(root.right, val) # 有# 中return root450. 删除二叉搜索树中的节点
思路:对于这种增删的,使用root.left and root.right来接受返回的节点值的!返回值来加入新节点, 这里也可以通过递归返回值删除节点!搜索树不用限定是用前中后序遍历,根据搜索树有序规则遍历就好了!但是还是要有递归三部曲的!!
- 确定单层递归的逻辑
这里就把二叉搜索树中删除节点遇到的情况都搞清楚。
有以下五种情况:
- 第一种情况:没找到删除的节点,遍历到空节点直接返回了
- 找到删除的节点
- 第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
- 第三种情况:删除节点的左孩子为空,右孩子不为空,删除节点,右孩子补位,返回右孩子为根节点
- 第四种情况:删除节点的右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点
- 第五种情况:左右孩子节点都不为空,则将删除节点的左子树头结点(左孩子)放到删除节点的右子树的最左面节点的左孩子上,返回删除节点右孩子为新的根节点。
第五种情况有点难以理解,看下面动画:
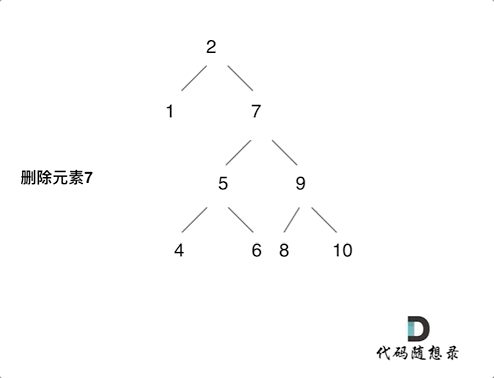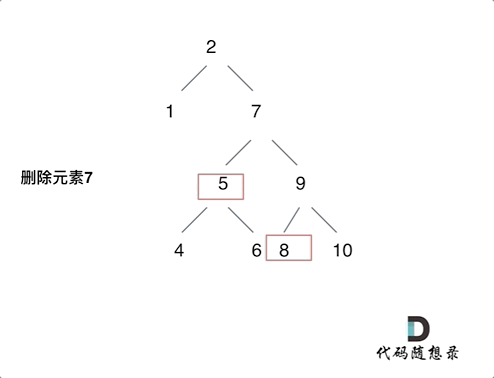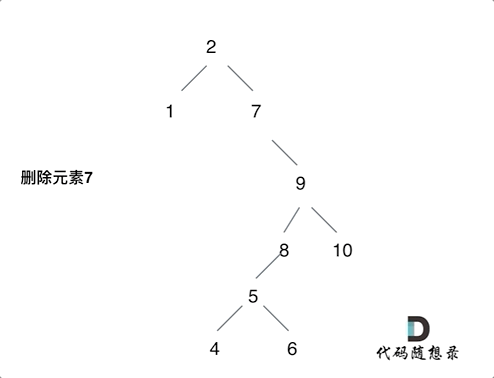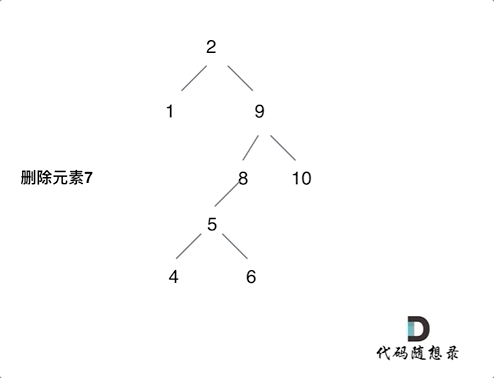
class Solution:def deleteNode(self, root, key):if root is None:return root# 单层逻辑if root.val == key:if root.left is None and root.right is None:return Noneelif root.left is None:return root.rightelif root.right is None:return root.leftelse:cur = root.rightwhile cur.left is not None:cur = cur.leftcur.left = root.leftreturn root.rightif root.val > key: # 左root.left = self.deleteNode(root.left, key)if root.val < key: # 右root.right = self.deleteNode(root.right, key)return root
相关文章:

2023-12-20 二叉搜索树的最近公共祖先和二叉搜索树中的插入操作和删除二叉搜索树中的节点
235. 二叉搜索树的最近公共祖先 思想:和二叉树的公共最近祖先节点的思路基本一致的!就是不用从下往上遍历处理!可以利用的二叉搜索树的特点从上往下处理了!而且最近公共节点肯定是第一个出现在【q,p】这个区间的内的&…...
pytorch文本分类(三)模型框架(DNNtextCNN)
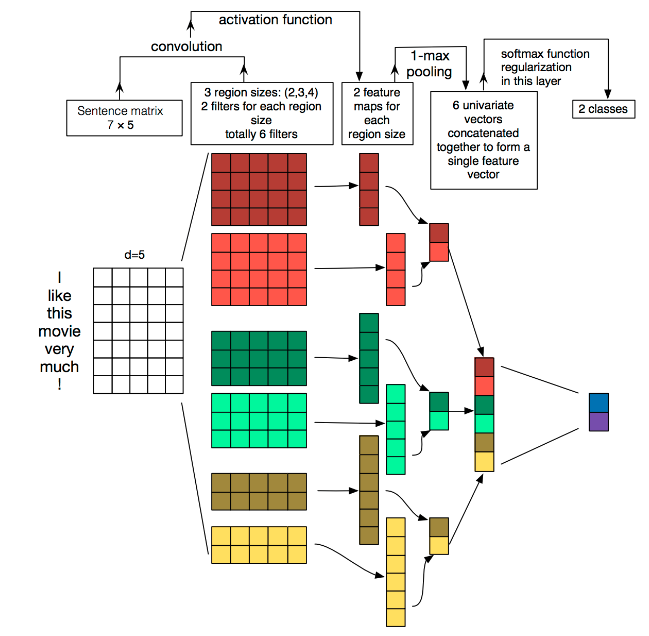
pytorch文本分类(三)模型框架(DNN&textCNN) 原任务链接 目录 pytorch文本分类(三)模型框架(DNN&textCNN)1. 背景知识深度学习 2. DNN2.1 从感知器到神经网络2.2 DNN的基本…...
<长篇文章!!>数据结构与算法的重要知识点与概要总结 ( •̀ ω •́ )✧✧临近考试和查漏补缺的小伙伴看这一篇就都懂啦~
目录 一、数据结构概论二、算法概论三、线性表四、栈五、队列六、串七、多维数组与矩阵八、广义表九、树与二叉树十、图 一、数据结构概论 1、数据元素和数据项 数据由数据元素组成,即数据元素是数据的基本单位,而数据元素又由若干个数据项组成…...

【安全】audispd调研
audispd调研 1 问题背景 在Linux中,当某个进程调用audit_set_pid将自己的pid保存到内核的audit模块后,如果有日志生成,kaudit内核线程就会通过netlink通信机制将审计日志发送给audit_pid,因此,只能有一个进程占用aud…...
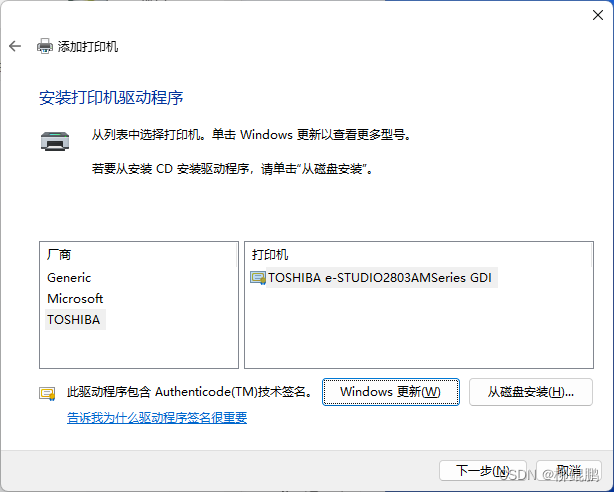
WINDOWS(WIN11)通过IP添加网络打印机
点击添加设备 点击手动添加 使用IP地址或主机名添加打印机 选择TCP/IP设备,输入打印机地址 如果有正确驱动就安装,没有就取消。 通过手动设置添加本地打印机或网络打印机 使用现有的端口 根据打印机IP,选择标准端口。 成功! 到…...

华为数通试题
选择题 华为数通推出的面向企业的云计算平台是? A) FusionSphere B) CloudEngine C) Agile Controller D) eSight 下面哪个不是华为数通的核心交换机系列? A) S12700 B) S5700 C) S9300 D) CloudEngine 华为数通的企业级路由器系列包括哪个?…...
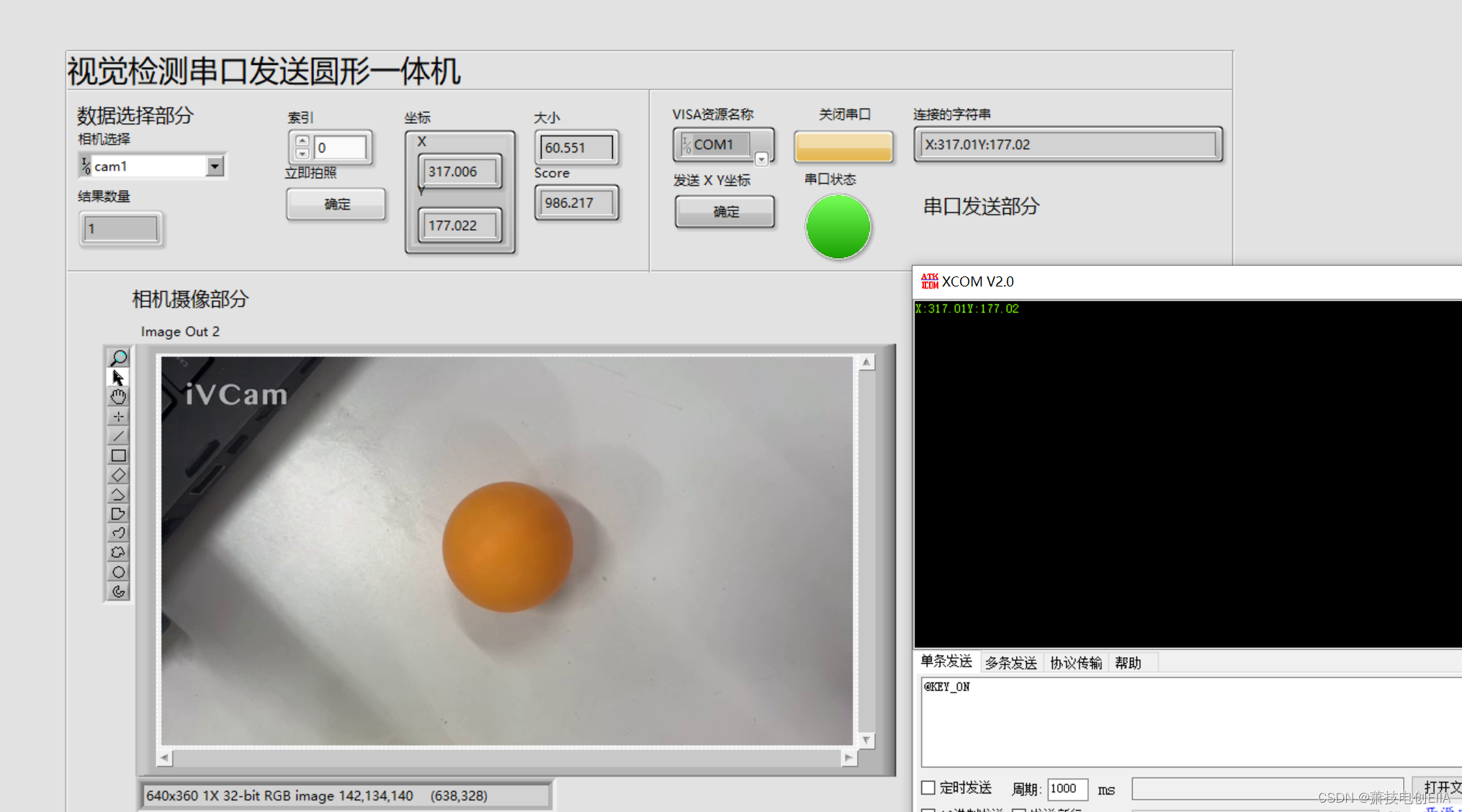
Labview Vision 机器视觉使用,从下载程序安装应用,到实战找硬币并输出值
1.前言 大家好,今天我要和机器人一起配合来打算 做机器视觉 用Labview 和 Vision 联动实现机器的视觉 2.下载软件-软件的安装 我们除了基础款的labview软件 还要安装视觉四件套 1.Labview 编程平台(我是 2023 q3) 2. NI - IMAQdx (驱动软…...

【delphi11】delphi基础探索【三、基础组件和事件】
目录 基础组件 1. TButton(按钮) 2. TLabel(标签) 3. TEdit(编辑框) 4. TMemo(多行编辑框) 5. TComboBox(组合框) 6. TCheckBox(复选框&…...

react hooks浅谈
一.useEffect useEffect是hooks中的生命周期函数 1.只要页面更新就触发回调: useEffect(() > { // 执行逻辑 }) 2.只运行一次(组件挂载和卸载时执行),第二个参数传空数组[]: useEffect(() > { // },[]) 3. 条件…...

stable diffusion webui之lora调用
1.触发词底模lora效果最好(分数不一定要取到1,0.8也行); 2.引用时一定要使用<lora:>,例如<lora:C4D_geometry_bg_v2.5:0.8>; "prompt": "(masterpiece:1.3), (best quality:1.…...

FormData文件上传多文件上传
一、简介 通常情况下,前端在使用post请求提交数据的时候,请求都是采用application/json 或 application/x-www-form-urlencoded编码类型,分别是借助JSON字符串来传递参数或者keyvalue格式字符串(多参数通过&进行连接&#…...
)
八股文打卡day4——计算机网络(4)
TCP和UDP的概念、特点、区别和对应的使用场景? 我的回答: 概念: TCP是传输控制协议,是面向连接、可靠的、基于字节流的传输层通信协议。 UDP是用户数据报协议,是无连接、不可靠的,基于数据报的传输层通信…...
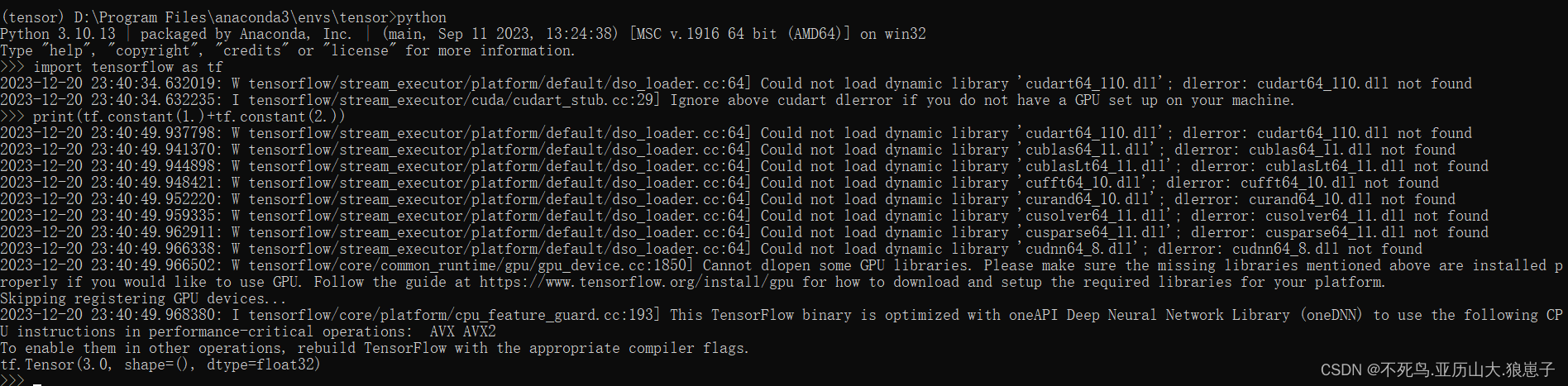
TensorFlow(2):Windows安装TensorFlow
1 安装python环境 这一步请自行安装,这边不做介绍。 2 安装anaconda 下载路径:Index of /,用户自行选择自己的需要的版本。 3 环境配置 3.1 anaconda环境配置 找到设置,点击系统->系统信息->高级系统设置->环境变量…...
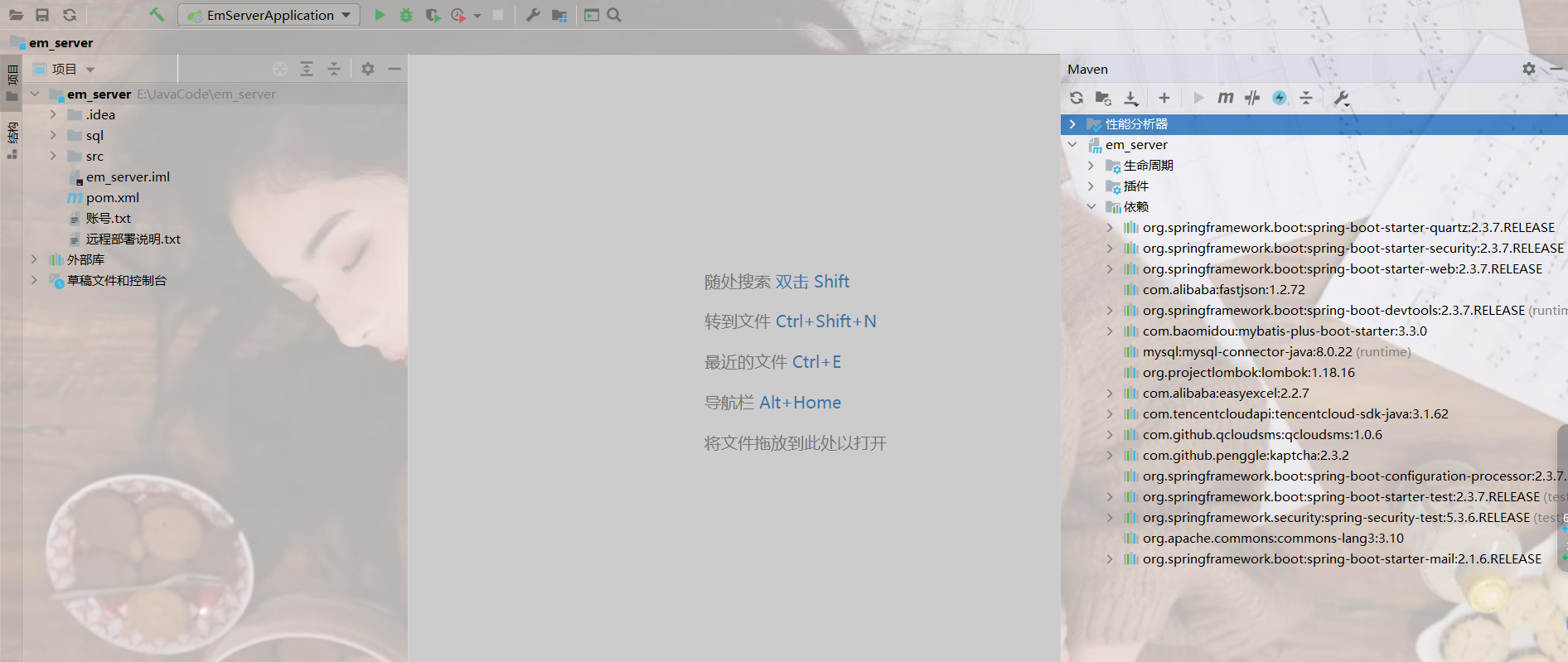
一文解决idea导入源码控制台爆红问题
文章目录 唠嗑部分背景说明idea查看maven配置 言归正传安装mavenidea配置maven 结语及资料获取 唠嗑部分 背景说明 很多新手伙伴们在导入项目源码时,都会遇到大片依赖爆红,项目跑不起来,小白也是把自己电脑重新配置了一番,复现了…...
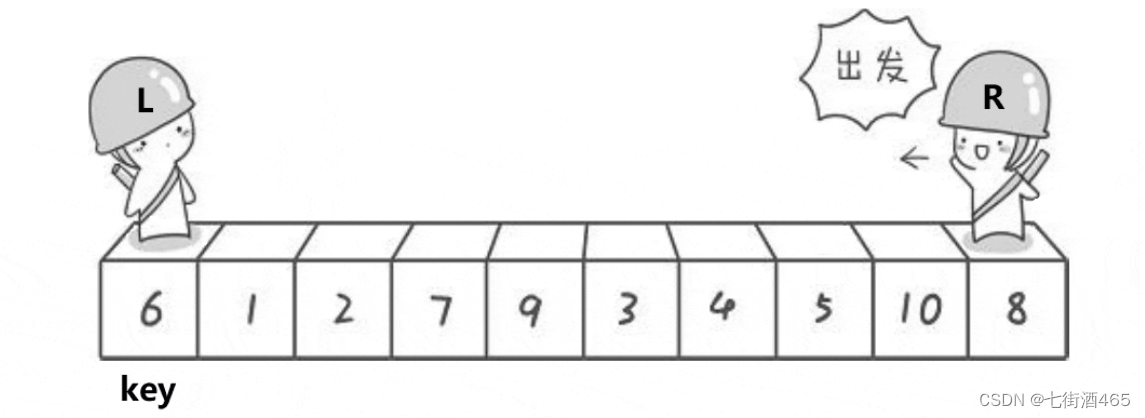
排序算法——快排
快速排序算法最早是由图灵奖获得者Tony Hoare设计出来的,他在形式化方法理论以 及ALGOL.60编程语言的发明中都有卓越的贡献,是20世纪最伟大的计算机科学家之—。 而这快速排序算法只是他众多贡献中的—个小发明而已。 快速排序(Quick Sort)的基本算法思…...
第二节TypeScript 基础语法
1、typescript程序由以下几个部分组成: 模块函数变量语句和表达式注释 2、开始第一个typescript程序 创建一个typescript程序,使之输出“hello typescript”: 代码: var message:string "hello typescript" cons…...
计算)
Go、Python、Java、JavaScript等语言的求余(取模)计算
余数符号规则: Go(%): 余数与被除数符号一致 Java(%): 余数与被除数符号一致 JavaScript(%): 余数与被除数符号一致 Python(%)…...

scrapy快加构造并发送请求
scrapy数据建模与请求 学习目标: 应用 在scrapy项目中进行建模应用 构造Request对象,并发送请求应用 利用meta参数在不同的解析函数中传递数据 1. 数据建模 通常在做项目的过程中,在items.py中进行数据建模 1.1 为什么建模 定义item即提前…...

【C++】谈谈深拷贝与浅拷贝
目录 一、浅拷贝 1.定义 2.示例 3.问题 二、深拷贝 1.定义 2.示例 3.优点 三、考虑场景 浅拷贝的考虑 1.性能要求 2.简单地数据结构 3.资源管理 深拷贝的考虑 1.动态内存分配 2.复杂数据结构 3.资源管理 总结 一、浅拷贝 1.定义 浅拷贝是指对对象进行复制时…...

电商API接口如何驱动业务:代码演示与解析
随着电子商务的飞速发展,电商平台的业务逻辑日益复杂,涉及的模块和功能也越来越多。在这个过程中,电商API接口扮演着至关重要的角色。通过API接口,不同的业务模块可以相互通信,实现数据和服务的共享,提高业…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...
