剑指offer题解合集——Week1day5
剑指offerWeek1
周五:重建二叉树
题目链接:重建二叉树
输入一棵二叉树前序遍历和中序遍历的结果,请重建该二叉树。注意:二叉树中每个节点的值都互不相同;
输入的前序遍历和中序遍历一定合法;
数据范围
树中节点数量范围 [0,100]
。样例
给定:
前序遍历是:[3, 9, 20, 15, 7]
中序遍历是:[9, 3, 15, 20, 7]返回:[3, 9, 20, null, null, 15, 7, null, null, null, null]
返回的二叉树如下所示:3/ \9 20/ \15 7
AC代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:unordered_map<int, int> map;TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {for (int i = 0; i < inorder.size(); i ++ ) map[inorder[i]] = i;return dfs(preorder, inorder, 0, preorder.size() - 1, 0, inorder.size() - 1);}TreeNode* dfs(vector<int>& preorder, vector<int>& inorder, int pl, int pr, int il, int ir){if (pl > pr) return nullptr;auto node = new TreeNode(preorder[pl]);int k = map[node->val];node->left = dfs(preorder, inorder, pl + 1, pl + k - il, il, k - 1);node->right = dfs(preorder, inorder, pl + k - il + 1, pr, k + 1, ir);return node;}
};
思路:
整体思路
要时刻牢记前序遍历、中序遍历的特点
前序:第一个遍历的一定是根节点
中序遍历:在根节点的左边一定是左子树,右边则是右子树那么两个性质结合,可以从前序遍历中找到根节点
然后再从中序遍历中,根据根节点划分左右子树
在左右子树中递归以上步骤,则可以重建二叉树本题还有一个难点:
当知道根节点以后,如何划分左右子树
别说什么:哎呀中序遍历知道根节点,左边的不就是左子树吗
注意,我这里指的是:在前序遍历的数集中划分左右子树
这里是利用左右子树区间长度相等得出区间边界
代码思路
- 利用map构造出中序遍历的值能索引到值对应的下标(为了更好的找到根节点)
- 递归,递归的条件是:前序遍历集存在
- 构造根节点
- 找到根节点的下标值
- 在左子树中递归
- 前序遍历区间:第一个节点是pl,也是根节点,因此左子树从pl + 1开始,左子树的右端点待定
- 中序遍历的区间:左端点为il,右端点为根节点的索引值 - 1
- 在右子树中递归
- 右子树
- 前序遍历区间:左端点待定,右端点显然是pr
- 中序遍历的区间:左端点为根节点的索引值 + 1,右端点ir
- 右子树
- 返回根节点
以上有两个待定的端点,也是难点
这里需要利用性质左右子树区间长度相等得出区间边界
记根节点下标为k
由于中序遍历中,左子树区间为[il, k - 1]
前序遍历[pl + 1, 待定]
记前序遍历区间的右端点为x
则有
x - pl - 1 + 1= k - 1 - il + 1
则可以解出x = k - il + pl
则前序遍历中,右子树的左端点显然为这个x + 1
部分模拟
前序遍历是:[3, 9, 20, 15, 7]
中序遍历是:[9, 3, 15, 20, 7]
- 前序遍历第一个节点为根节点,显然为3
- 从中序遍历中得到3,因此9是左子树,15, 20, 7是右子树
- 左子树已经确定
- 右子树中继续递归即可,例如,右子树的根为20(前序遍历中得出)
相关文章:

剑指offer题解合集——Week1day5
剑指offerWeek1 周五:重建二叉树 题目链接:重建二叉树 输入一棵二叉树前序遍历和中序遍历的结果,请重建该二叉树。注意:二叉树中每个节点的值都互不相同; 输入的前序遍历和中序遍历一定合法; 数据范围 树中节点数量…...
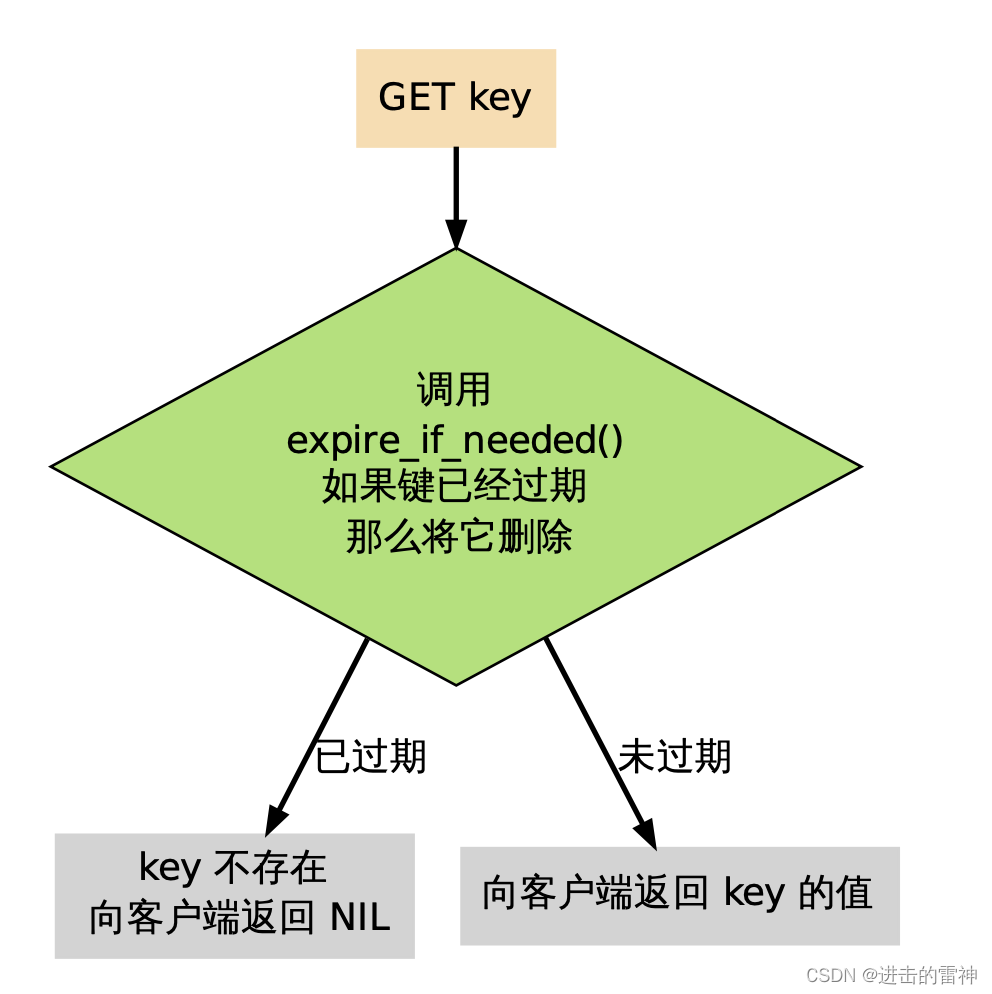
Redis设计与实现之数据库
目录 一、数据库 1、数据库的结构 2、 数据库的切换 3、 数据库键空间 4、键空间的操作 添加新键 删除键 更新键 取值 其他操作 5、 键的过期时间 6、过期时间的保存 7、设置生存时间 8、过期键的判定 9、 过期键的清除 定时删除 惰性删除 定期删除 10、过期…...
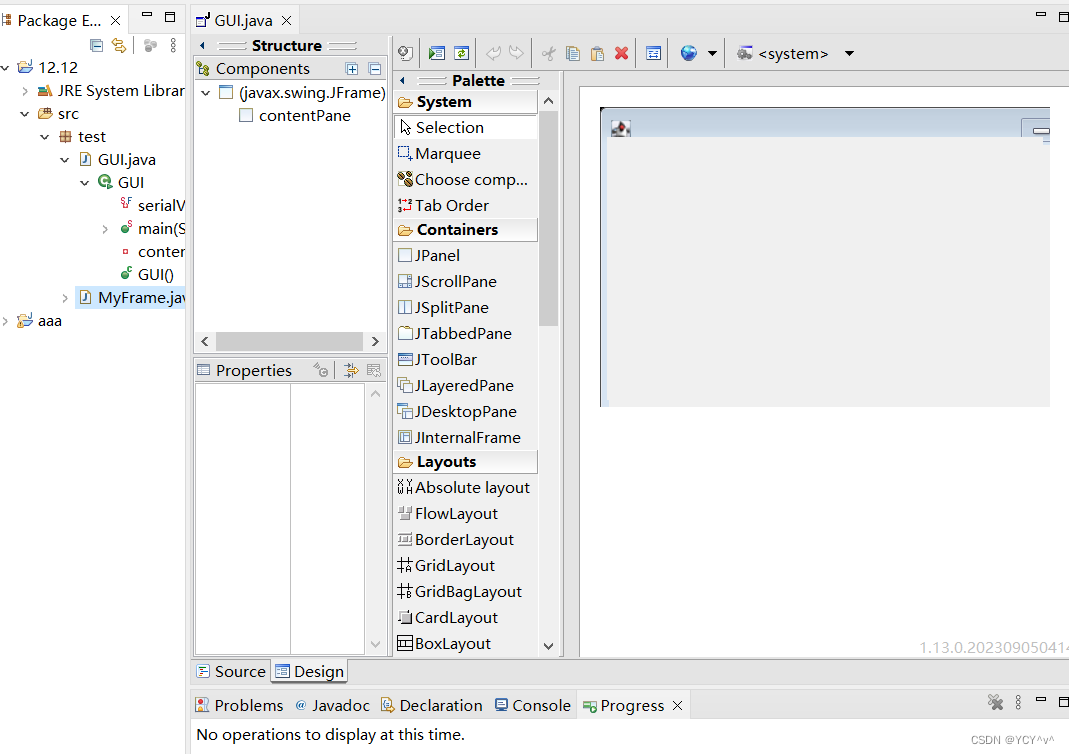
如何在Eclipse中安装WindowBuilder插件,详解过程
第一步:找到自己安装eclipse的版本,在Help-关于eclipse里面,即Version 第二步:去下面这个网站找到对应的 link(Update Site),这一步很重要,不然版本下载错了之后还得删除WindowBuil…...
node.js mongoose schemaTypes
目录 官方文档 简介 SchemaType 示例 配置SchemaType规则 通用规则 特定schemaType规则 String Number Date Map monggose会根据shcemaType将文档值转换成指定的类型 官方文档 Mongoose v8.0.3: SchemaTypes 简介 SchemaTypes是在使用Mongoose时,用于…...
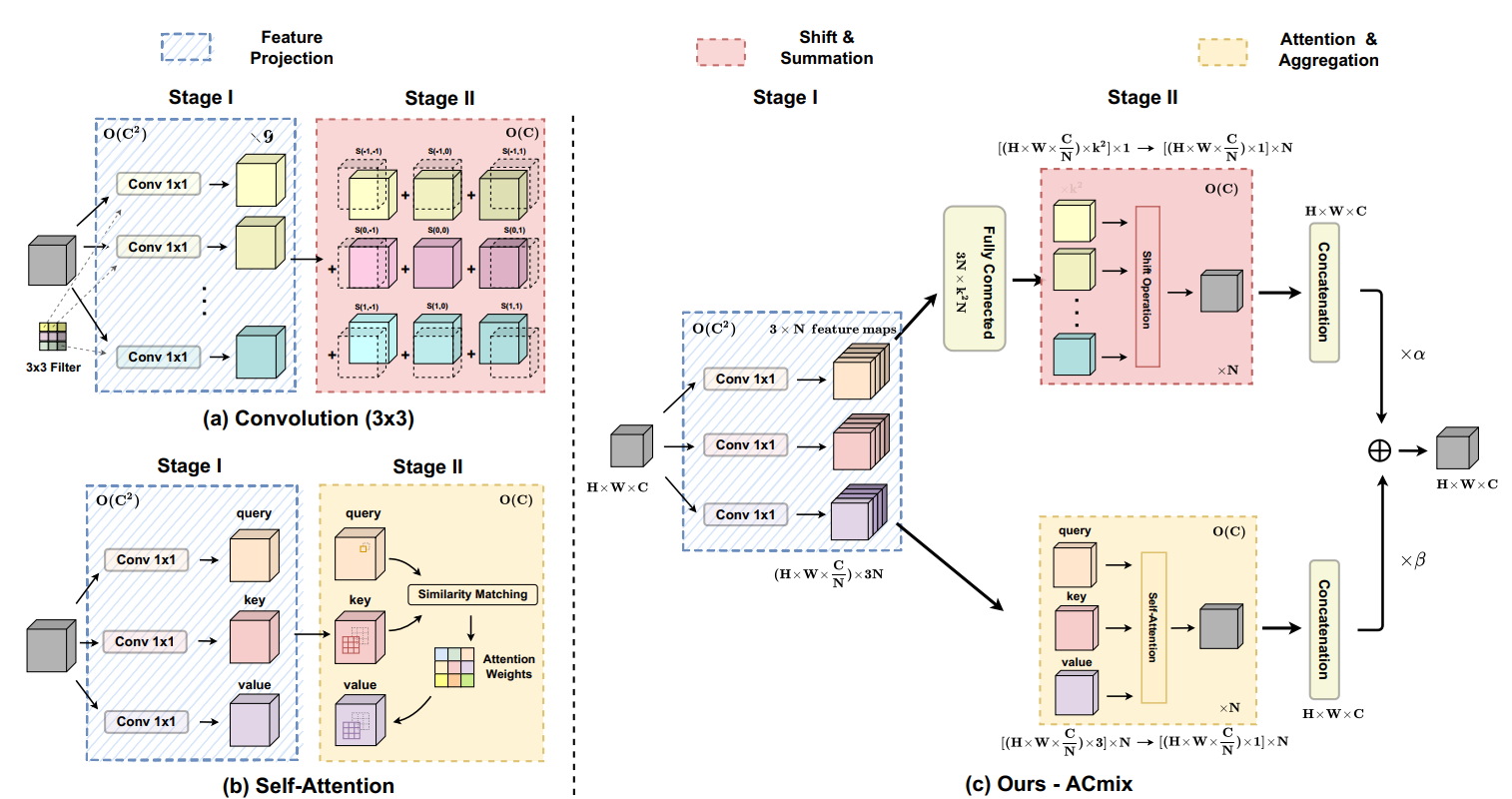
论文解读:On the Integration of Self-Attention and Convolution
自注意力机制与卷积结合:On the Integration of Self-Attention and Convolution(CVPR2022) 引言 1:卷积可以接受比较大的图片的,但自注意力机制如果图片特别大的话,运算规模会特别大,即上图中右边(卷积)会算得比较快…...

【Spring】15 ApplicationContextAware 接口
文章目录 1. 简介2. 作用3. 使用3.1 创建并实现接口3.2 配置 Bean 信息3.3 创建启动类3.4 启动 4. 应用场景总结 Spring 框架提供了许多回调接口,用于在 Bean 的生命周期中执行特定的操作。ApplicationContextAware 接口是其中之一,它允许 Bean 获取对 A…...

Android 版本控制工具--Git
要在Android中使用Git,需要进行以下步骤: 安装Git:首先在你的开发环境中安装Git。在Windows中,你可以从官方网站(https://git-scm.com/downloads)上下载Git的可执行文件并进行安装。在Mac上,你可…...

Wireshark高级网络安全分析
第一章:Wireshark基础及捕获技巧 1.1 Wireshark基础知识回顾 1.2 高级捕获技巧:过滤器和捕获选项 1.3 Wireshark与其他抓包工具的比较 第二章:网络协议分析 2.1 网络协议分析:TCP、UDP、ICMP等 2.2 高级协议分析:HTTP…...
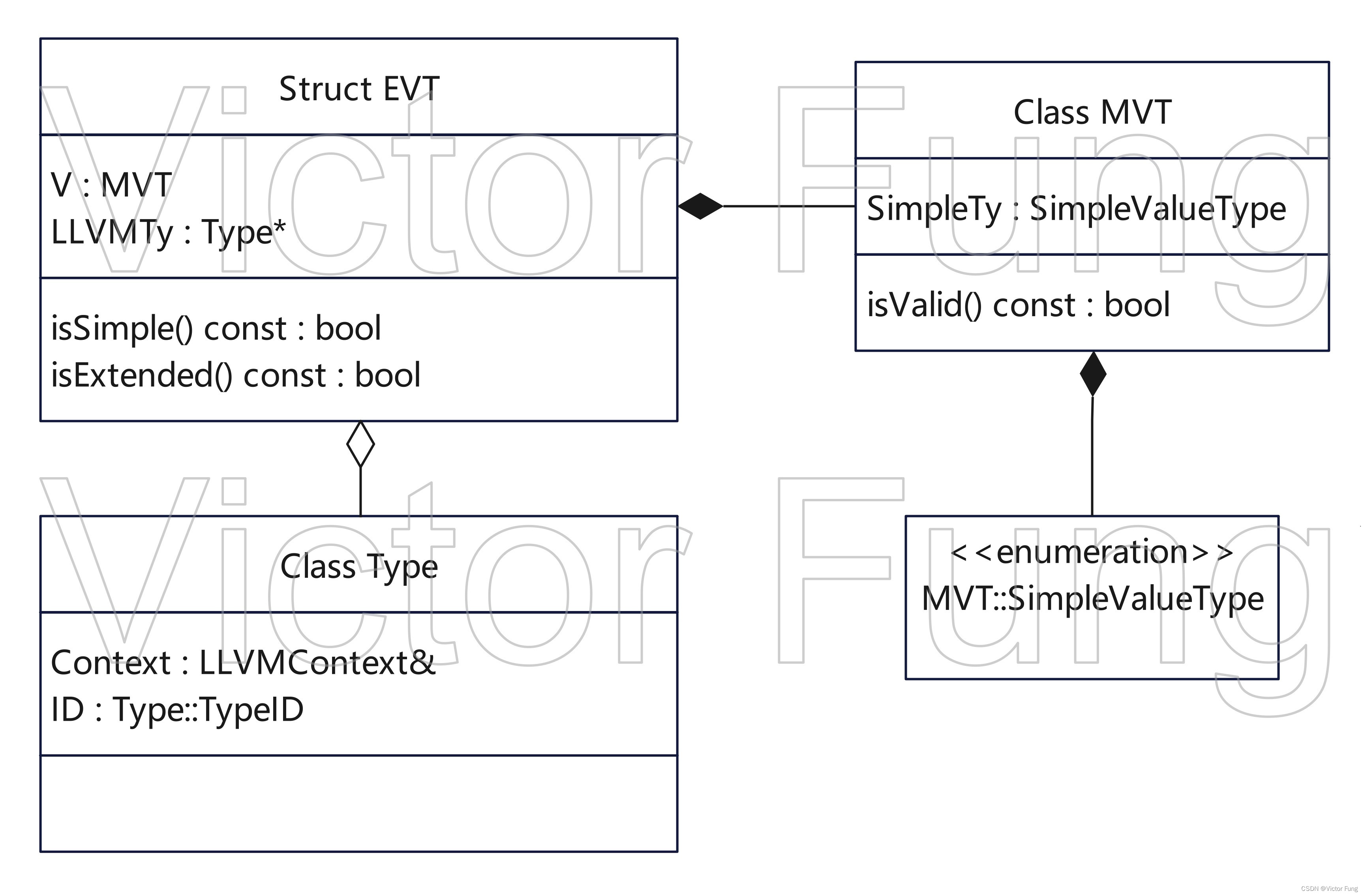
llvm后端之DAG设计
llvm后端之DAG设计 引言1 核心类设计2 类型系统2.1 MVT::SimpleValueType2.2 MVT2.3 EVT 3 节点类型 引言 llvm后端将中端的IR转为有向无环图,即DAG。如下图: 图中黑色箭头为数据依赖;蓝色线和红色线为控制依赖。蓝色表示指令序列化时两个节…...
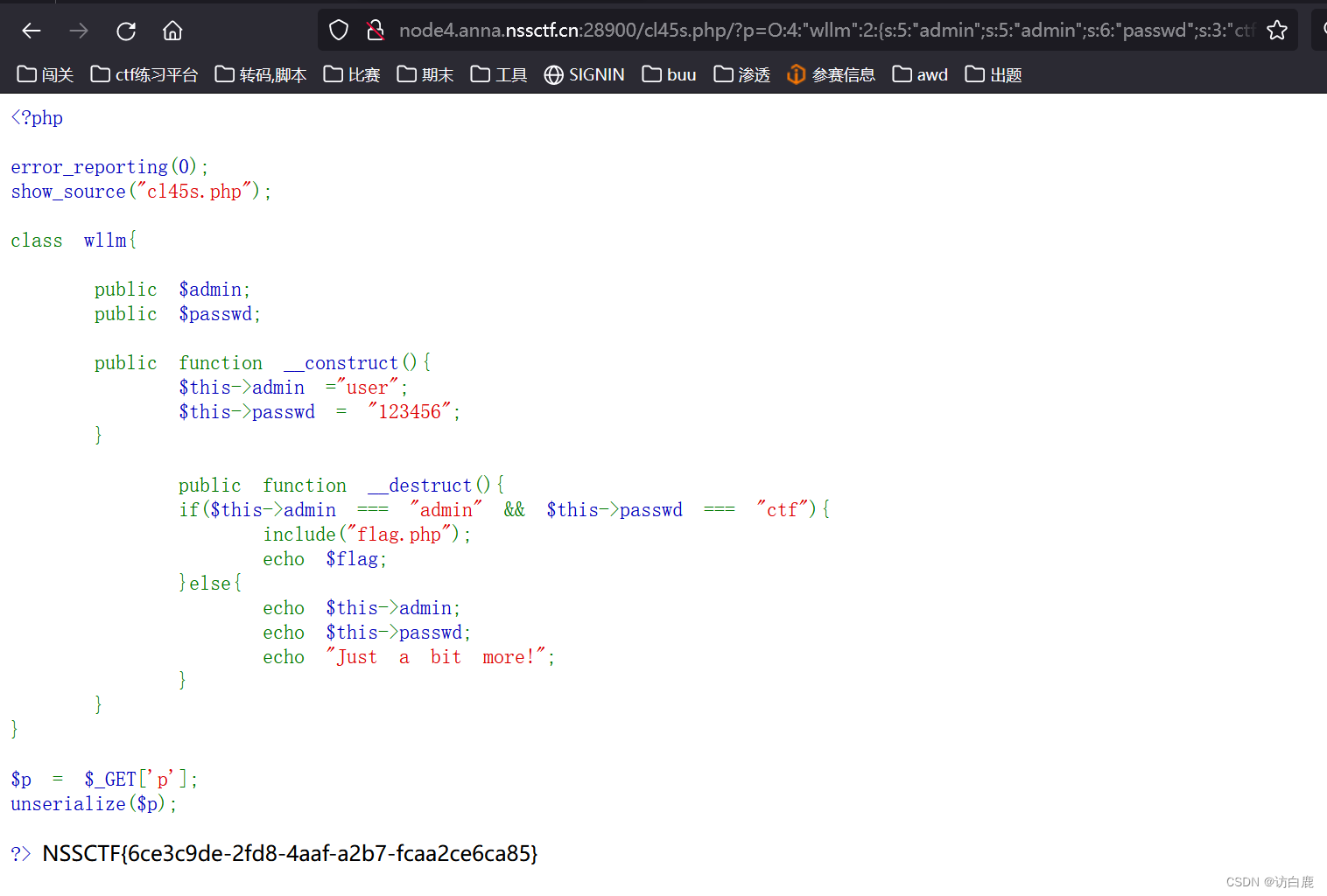
反序列化 [SWPUCTF 2021 新生赛]ez_unserialize
打开题目 查看源代码 得到提示,那我们用御剑扫描一下看看 我们知道有个robots.txt,访问一下得到 那我们便访问一下 cl45s.php看看 得到网站源代码 <?phperror_reporting(0); show_source("cl45s.php");class wllm{public $admin;public …...
centos(linux)安装jenkins
官网:https://pkg.jenkins.io/redhat/ 安装官网进行操作: sudo wget -O /etc/yum.repos.d/jenkins.repo https://pkg.jenkins.io/redhat/jenkins.reposudo rpm --import https://pkg.jenkins.io/redhat/jenkins.io-2023.key若出现如下错误: …...

Wireshark统计和可视化
第一章:Wireshark基础及捕获技巧 1.1 Wireshark基础知识回顾 1.2 高级捕获技巧:过滤器和捕获选项 1.3 Wireshark与其他抓包工具的比较 第二章:网络协议分析 2.1 网络协议分析:TCP、UDP、ICMP等 2.2 高级协议分析:HTTP…...

高通平台开发系列讲解(SIM卡篇)SIM软件架构介绍
文章目录 一、SIM软件架构二、MMG SDI Task三、GSTK Task四、Simlock Task沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇文章将介绍SIM的相关组件。 SIM软件架构: SIM软件架构指的是与SIM卡(Subscriber Identity Module,订阅者身份模块)相关的软件系统设计和…...

音频筑基:瞬态、基音、偏噪信号类型分析
音频筑基:瞬态、基音、偏噪信号类型分析 是什么深入理解从编码角度看,基音信号编码通常会有啥问题?在频域感知编码过程中,瞬态信号会有啥问题?如何解决?瞬态信号场景下,5/10ms帧长编码有啥区别&…...

HarmonyOS ArkTS 中DatePicker先择时间 路由跳转并传值到其它页
效果 代码 代码里有TextTimerController 这一种例用方法较怪,Text ,Button Datepicker 的使用。 import router from ohos.router’则是引入路由模块。 import router from ohos.router Entry Component struct TextnewClock {textTimerController: TextTimerContr…...
Axure RP 8 for Mac/win中文版:打造完美交互式原型设计体验
Axure RP 8,一款引领潮流的交互式原型设计工具,为设计师提供了无限的可能性,让他们能够创造出逼真的原型,从而更好地展示和测试他们的设计。 Axure RP 8拥有丰富的功能和工具,让设计师可以轻松地创建出复杂的交互式原…...

迪文屏开发保姆级教程——页面键盘
迪文屏页面键盘保姆级教程。 本篇文章主要介绍了在DGBUS平台上使用页面键盘的步骤。 迪文屏官方开发指南PDF:(不方便下载的私聊我发给你) https://download.csdn.net/download/qq_21370051/88647174?spm1001.2014.3001.5503https://downloa…...

Unity的UI界面——Text/Image
编辑UI界面时,要先切换到2d界面 (3d项目的话) 1.Text控件 Text控件的相关属性: Character:(字符) Font:字体 Font Style:字体样式 Font Size:字体大小 Line Spac…...

sklearn和tensorflow的理解
人工智能的实现是基于机器学习,机器学习的一个方法是神经网络,以及各种机器学习算法库。 有监督学习:一般数据构成是【特征值目标值】 无监督学习:一般数据构成是【特征值】 Scikit-learn(sklearn)的定位是通用机器学习库&…...

css中BFC
css BFC BFC具有以下特性创建BFC的方式有多种BFC的应用场景和作用 扩展: CSS动画 transition: 过渡动画animation / keyframestransform都有哪些属性 举例 css BFC BFC,即块级格式化上下文(Block Formatting Context)…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...
