大数据HCIE成神之路之数据预处理(3)——数值离散化
数值离散化
- 1.1 无监督连续变量的离散化 – 聚类划分
- 1.1.1 实验任务
- 1.1.1.1 实验背景
- 1.1.1.2 实验目标
- 1.1.1.3 实验数据解析
- 1.1.2 实验思路
- 1.1.3 实验操作步骤
- 1.1.4 结果验证
- 1.2 无监督连续变量的离散化 – 等宽划分
- 1.2.1 实验任务
- 1.2.1.1 实验背景
- 1.2.1.2 实验目标
- 1.2.1.3 实验数据解析
- 1.2.2 实验思路
- 1.2.3 实验操作步骤
- 1.2.4 结果验证
- 1.3 无监督连续变量的离散化 – 等频划分
- 1.3.1 实验任务
- 1.3.1.1 实验背景
- 1.3.1.2 实验目标
- 1.3.1.3 实验数据解析
- 1.3.2 实验思路
- 1.3.3 实验操作步骤
- 1.3.4 结果验证
- 1.4 有监督连续变量的离散化 – 基于卡方检验的方法
- 1.4.1 实验任务
- 1.4.1.1 实验背景
- 1.4.1.2 实验目标
- 1.4.1.3 实验数据解析
- 1.4.2 实验思路
- 1.4.3 实验操作步骤
- 1.4.4 结果验证
1.1 无监督连续变量的离散化 – 聚类划分
聚类划分 是指使用聚类算法将数据分为K类,需要自己设定K值大小。从而把同属一类的数值标记为相同标签。目前常用的聚类划分方法是Kmeans算法。
聚类划分的实现使用Python中sklearn库的KMeans ( ) 函数,其基本格式如下:
KMeans(n_clusters=8, init='k-means++', n_init=10, max_iter=300, tol=0.0001, precompute_distances='auto', verbose=0, random_state=None, copy_x=True, n_jobs=1, algorithm='auto')
关键参数详解:
- n_clusters=8,表示要分成的簇数,默认为8。
- init=‘k-means++’,表示初始化质心,默认采用k-means++,是一种生成初始质心的算法。
- n_init=10,表示选择的质心种子次数,默认为10次。返回质心最好的一次结果,即计算时长最短的一次结果)。
- max_iter=300,表示每次迭代的最大次数,默认为300。
- tol=0.0001,表示容忍的最小误差,当误差小于tol就会退出迭代,默认值为0.0001。
- precompute_distances=auto,这个参数会在空间和时间之间做权衡,如果是True会把整个距离矩阵都放到内存中,auto状态下会默认在数据样本大于featurs*samples 的数量时则False。
- verbose=0,表示是否输出详细信息 。
- random_state=None,表示随机生成器的种子,和初始化中心有关。
- copy_x=True,表示是否对输入数据继续copy 操作,以便不修改用户的输入数据。
- n_jobs=1,表示使用进程的数量,默认为1。
1.1.1 实验任务
1.1.1.1 实验背景
KMeans是最简单的聚类算法之一,但是运用十分广泛。KMeans一般在数据分析前期使用,选取适当的k,将数据分类后,然后分类研究不同聚类下数据的特点。
1.1.1.2 实验目标
掌握对数据进行KMeans聚类划分的操作。
1.1.1.3 实验数据解析
数据使用鸢尾花数据集。
1.1.2 实验思路
-
导入实验数据集。
-
使用KMean( )函数对数据进行聚类划分并可视化展示出来。
1.1.3 实验操作步骤
步骤 1 导入数据集
iris是150*4的数据集,为实验过程更易被理解。特取其中2-4列的数据进行聚类划分实验。
import numpy as np
from sklearn.datasets import load_iris
iris=load_iris()
# 只取数据集中的 3列【petal length (cm)】、4列【petal width (cm)】的数据
X = iris.data[:, 2:4]
X的部分结果如下:
array([[1.4, 0.2],[1.4, 0.2],[1.3, 0.2],[1.5, 0.2],[1.4, 0.2],[1.7, 0.4],[1.4, 0.3],[1.5, 0.2],[1.4, 0.2],
步骤 2 聚类划分
# 导入 KMeans 包
from sklearn.cluster import KMeans
# 构造聚类器实例
estimator = KMeans(n_clusters=3)
# 聚类
estimator.fit(X)
# 获取聚类标签
label_pred = estimator.labels_
补充:
label_pred 的结果如下:
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,0, 0, 0, 0, 0, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2,2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1,1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1,1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])
打印 label_pred==0 的值:
x0 = X[label_pred == 0]
x0
部分结果显示如下:
array([[1.4, 0.2],[1.4, 0.2],[1.3, 0.2],[1.5, 0.2],[1.4, 0.2],[1.7, 0.4],[1.4, 0.3],[1.5, 0.2],[1.4, 0.2],[1.5, 0.1],[1.5, 0.2],[1.6, 0.2],
解释: label_pred 的元素个数与 X 的行数是一样的(因为一个标签,对应一行数据), label_pred 的元素值如果为0,则为True, X[label_pred == 0] 其实就是把为True的对应位置的元素保留了下来,所以就相当于实现了筛选。
步骤 3 可视化展示聚类划分结果
# 导入可视化包
import matplotlib.pyplot as plt
# 可视化 k-means 结果
# 设置测试数据
x0 = X[label_pred == 0]
x1 = X[label_pred == 1]
x2 = X[label_pred == 2]
# 设置绘制的图像为散点图,输入数据 x0,散点的颜色为红色,散点的形状为 o,标签为label0
plt.scatter(x0[:, 0], x0[:, 1], c="red", marker='o',label='label0')
# 设置绘制的图像为散点图,输入数据 x1,散点的颜色为绿色,散点的形状为*,标签为label1
plt.scatter(x1[:, 0], x1[:, 1], c="green", marker='*',label='label1')
# 设置绘制的图像为散点图,输入数据 x2,散点的颜色为蓝色,散点的形状为+,标签为label2
plt.scatter(x2[:, 0], x2[:, 1], c="blue", marker='+',label='label2')
# 设置 x 轴标题为'petal length'
plt.xlabel('petal length')
# 设置 y 轴标题为'petal width'
plt.ylabel('petal width')
# 设置图例显示的位置为左上角
plt.legend(loc=2)
# 显示可视化结果
plt.show()
输出结果如下:

扩展学习:
下面是一些常用的estimator属性和方法:
labels_ :聚类标签。它是一个大小为 n_samples 的一维数组,表示每个样本所属的聚类簇的标签。
label_pred = estimator.labels_
cluster_centers_ :聚类中心。它是一个大小为 (n_clusters, n_features) 的二维数组,表示每个聚类簇的中心点的坐标。
centers = estimator.cluster_centers_
inertia_ :聚类内部的平方和误差 (SSE) 。它是一个标量值,表示所有样本到其所属聚类中心的距离的总和。
sse = estimator.inertia_
n_clusters :聚类的 数量 。它是一个整数,表示聚类器指定的聚类簇的个数。
num_clusters = estimator.n_clusters
fit(X) :对数据进行聚类。X是一个大小为 (n_samples, n_features) 的二维数组,表示输入的特征数据。
estimator.fit(X)
fit_predict(X) :对数据进行聚类,并返回聚类 标签 。
labels = estimator.fit_predict(X)
整理成表格如下:
| 属性/方法 | 描述 |
|---|---|
labels_ | 聚类标签。大小为 n_samples 的一维数组,表示每个样本所属的聚类簇的标签。 |
cluster_centers_ | 聚类中心。大小为 (n_clusters, n_features) 的二维数组,表示每个聚类簇的中心点的坐标。 |
inertia_ | 聚类内部平方和误差(SSE)。标量值,表示所有样本到其所属聚类中心的距离的总和。 |
n_clusters | 聚类的数量。整数,表示聚类器指定的聚类簇的个数。 |
fit(X) | 对数据进行聚类。X 是一个大小为 (n_samples, n_features) 的二维数组,表示输入的特征数据。 |
fit_predict(X) | 对数据进行聚类,并返回聚类标签。 |
这些属性和方法可以帮助你使用KMeans聚类器进行聚类操作,并获取聚类结果、聚类中心以及聚类质量的评估。你可以根据具体的需求选择适当的属性或方法来处理聚类结果。
1.1.4 结果验证
由上述实验结果可知,使用 k-means 方法对鸢尾花部分数据集进行聚类划分之后将数据的分成了三类,几乎没有数据点是异常的。
1.2 无监督连续变量的离散化 – 等宽划分
等宽划分 是指把连续变量按照相同的区间间隔划分几等份。换句话说,就是根据连续变量的 最大值 和 最小值 ,将变量划分为N等份。
等宽划分的实现使用Python中pandas库的cut ( ) 函数,其基本格式如下:
pandas.cut(x,bins,right=True,labels=None,retbins=False,precision=3,include_lowest=False)
关键参数详解:
- x,表示进行划分的
一维数组。 - bins,定义分箱边界的标准,表示将x划分为多少个等间距的区间。
- right=True,是否包含右端点,表示是否包含箱子的最右边的边界。如果right=True,那么箱子[1, 2, 3, 4]表示(1,2], (2,3], (3,4]。
- labels=None,指定返回的箱子的标签,表示是否用标记来代替返回的bins,必须与结果的箱子长度相同。
- retbins=False,表示是否返回箱子。默认为False,False 则返回x中每个值对应的bin的列表,Ture则返回x中每个值对应的bin的列表和对应的bins。
- precision=3,表示存储和显示箱子标签的精度,默认为3,表示返回的数据将包含三位小数。
- include_lowest=False,表示是否包含左端点,表示第一个区间是否应该是左包含的。
1.2.1 实验任务
1.2.1.1 实验背景
可以使用cut( )函数进行等宽划分,按照相同宽度将数据分成几等份。缺点是受到异常值的影响比较大。
1.2.1.2 实验目标
掌握对数据进行等宽划分的操作。
1.2.1.3 实验数据解析
实验使用鸢尾花数据集。
1.2.2 实验思路
- 导入实验数据集。
- 使用cut ( )函数对数据进行等宽划分。
1.2.3 实验操作步骤
步骤 1 数据准备
import pandas as pd
from sklearn.datasets import load_iris
iris=load_iris()
X=iris.data[:,1]
步骤 2 等宽划分
#指定分段的段数为 5
x=pd.cut(X,5)
x
输出结果如下:
[(3.44, 3.92], (2.96, 3.44], (2.96, 3.44], (2.96, 3.44], (3.44, 3.92], ..., (2.96, 3.44], (2.48, 2.96], (2.96, 3.44], (2.96, 3.44], (2.96, 3.44]]
Length: 150
Categories (5, interval[float64]): [(1.998, 2.48] < (2.48, 2.96] < (2.96, 3.44] < (3.44, 3.92] < (3.92, 4.4]]
扩展:加上retbins=True
pd.cut(X, 5, retbins = True)
则多打印一行:
array([1.9976, 2.48 , 2.96 , 3.44 , 3.92 , 4.4 ]))
上面这六个数,其实就是分隔区间的边界值。
1.2.4 结果验证
系统自动将数据划分为(1.998, 2.48]、 (2.48, 2.96] 、(2.96, 3.44] 、(3.44, 3.92] 、(3.92, 4.4]五个等宽区间,并将原本的数据集中的 数据对应的区间显 示出来。
思考:为什么精度是3位小数,但是结果有一些是3位,有一些是两位,有一些是一位?
回答:precision参数可以控制分箱边界的最大小数位数,但实际的小数位数还取决于数据的分布。比如4.400其实也就是4.4,就没必要写4.400了。
1.3 无监督连续变量的离散化 – 等频划分
把连续变量划分几等份,保证每份的数值个数相同。具体来说,假设共有M个数值,划分N份,每份包含(M/N)个数值,使用Python中pandas库的qcut() 函数,其基本格式如下:
qcut(x, q, labels=None, retbins=False, precision=3, duplicates='raise')
关键参数详解:
- x,表示进行划分的
一维数组。 - q,表示划分的组数。
- labels=None,表示是否用标记来代替返回的bins。
- retbins=False,表示返回值,False 代表返回x中每个值对应的bin的列表,Ture代表返回x中每个值对应的bin的列表和对应的bins。
- precision=3,表示精度,默认为3。
- duplicates如果bin值边缘不唯一,就提高错误值或删除非唯一性。
1.3.1 实验任务
1.3.1.1 实验背景
我们可以使用qcut( )函数进行等频划分,将数据分成几等份,每等份数据里面的个数是一样的。
1.3.1.2 实验目标
掌握使用qcut函数实现数据的等频划分。
1.3.1.3 实验数据解析
实验使用鸢尾花数据集。
1.3.2 实验思路
-
导入实验数据集。
-
使用qcut ( )函数对数据进行等频划分。
1.3.3 实验操作步骤
步骤 1 数据准备
iris是150*4的数据集,特取其中一个属性进行等频划分实验。
import pandas as pd
from sklearn.datasets import load_iris
iris=load_iris()
X=iris.data[:,1]
步骤 2 等频划分
#指定分段的段数为 5
x=pd.qcut(X,5)
x
输出结果如下:
[(3.4, 4.4], (2.7, 3.0], (3.1, 3.4], (3.0, 3.1], (3.4, 4.4], ..., (2.7, 3.0], (1.999, 2.7], (2.7, 3.0], (3.1, 3.4], (2.7, 3.0]]
Length: 150
Categories (5, interval[float64]): [(1.999, 2.7] < (2.7, 3.0] < (3.0, 3.1] < (3.1, 3.4] < (3.4, 4.4]]
1.3.4 结果验证
系统自动将数据划分为(1.999, 2.7] 、(2.7, 3.0] 、(3.0, 3.1] 、(3.1, 3.4] 、(3.4, 4.4]五个等频区间。
补充一(precision参数的说明):
例如,如果我们有一个数据范围从0.123456到1.123456,我们想要将其划分为两个箱子,那么:
如果我们设置precision=2,那么我们得到的箱子边界将是(0.12, 0.62]和(0.62, 1.12]。
如果我们设置precision=3,那么我们得到的箱子边界将是(0.123, 0.623]和(0.623, 1.123]。
因此,precision参数影响了分箱标签的精度,这可能会影响我们对数据的理解和解释。但是,它并不会改变实际的分箱过程,也就是说,数据仍然会被均匀地分配到每个箱子中。
补充二(什么是等距分箱?什么是等频分箱):
-
等距分箱:是最为常用的分箱方法之一,从最小值到最大值之间,均分为N等份,如果A,B为最小最大值,则每个区间的长度为W=(B−A)/N,则区间边界值为A+W,A+2W,….A+(N−1)W。这里只考虑边界,每个等份里面的实例数量可能不等。
-
等频分箱:区间的边界值要经过选择,使得每个区间包含大致相等的实例数量。比如说 N=10,每个区间应该包含大约10%的实例。
这两种分箱方法都是无监督的分箱方法,只根据变量值的分布来划分区间,不需要有目标变量(标签)。
1.4 有监督连续变量的离散化 – 基于卡方检验的方法
该方法是一种自底向上的方法,运用卡方检验的策略,自底向上合并数值进行有监督离散化,核心操作是Merge。将数据集里的数值当做单独区间,递归找出可合并的最佳临近区间。判断可合并区间用到卡方统计量来检测两个区间的相关性,对符合所设定阀值的区间进行合并。常用的方法有ChiMerge、Chi2、Chi-Square Measure,下面对Chi2方法详细说明。
基于卡方检验的数值特征离散化的实现使用Python中scipy.stats统计函数库中的chi2 ( ) 函数,其基本使用格式如下:
chi2(X, y)
关键参数详解:
- X,样本数据。
- y,目标数据。
1.4.1 实验任务
1.4.1.1 实验背景
我们可以使用chi2 ( )函数进行卡方检验,这是一种基础的常用假设检验方法。
1.4.1.2 实验目标
掌握使用chi2 ( )函数实现数据集的卡方分箱操作。
1.4.1.3 实验数据解析
实验使用鸢尾花数据集。
1.4.2 实验思路
- 导入实验数据集。
- 使用chi2 ( )函数对数据进行基于卡方检验的有监督连续变量的离散化。
1.4.3 实验操作步骤
步骤 1 导入数据集
import pandas as pd
from sklearn.datasets import load_iris
iris=load_iris()# 对数据集做基于卡方检验的有监督连续变量的离散化。
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
# 选择 K 个最好的特征,返回选择特征后的数据
SelectKBest(chi2, k=2).fit_transform(iris.data, iris.target)
输出的部分结果如下:
# 输出结果
array([[1.4, 0.2],
[1.4, 0.2],
[1.3, 0.2],
[1.5, 0.2],
[1.4, 0.2],
[1.7, 0.4],
1.4.4 结果验证
由上述实验结果可知,原先没有规律的数据经过卡方检验操作后,对每个样本进行了有监督连续变量的离散化,从 Iris 数据集中选择的两个最佳特征是 “花瓣长度 (cm)” 和 “花瓣宽度 (cm)”。这两个特征被认为与目标变量具有较高的相关性,因此被选择作为特征子集。提示,虽然特征选择可能是数据预处理的一部分,但它着重于选择最重要的特征,而不是对数据进行转换或清洗。因此,在上述例子中,我们可以将其归类为特征选择相关的知识。
相关文章:

大数据HCIE成神之路之数据预处理(3)——数值离散化
数值离散化 1.1 无监督连续变量的离散化 – 聚类划分1.1.1 实验任务1.1.1.1 实验背景1.1.1.2 实验目标1.1.1.3 实验数据解析 1.1.2 实验思路1.1.3 实验操作步骤1.1.4 结果验证 1.2 无监督连续变量的离散化 – 等宽划分1.2.1 实验任务1.2.1.1 实验背景1.2.1.2 实验目标1.2.1.3 实…...
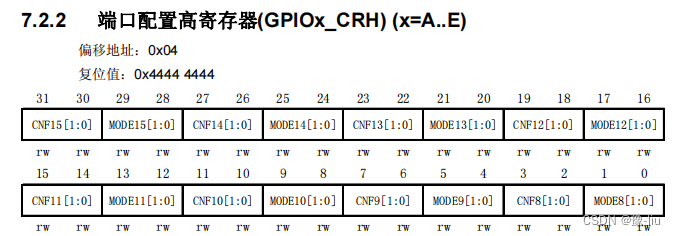
stm32 寄存器、地址、位带操作
存储器区域功能划分 4GB 的地址空间中,ARM 已经粗线条的平均分成了 8 个块,每块 512MB,每个块也都规定了用途,具体分类见表格 6-1。每个块的大小都有 512MB,显然这是非常大的,芯片厂商在每个块的范围内设计…...
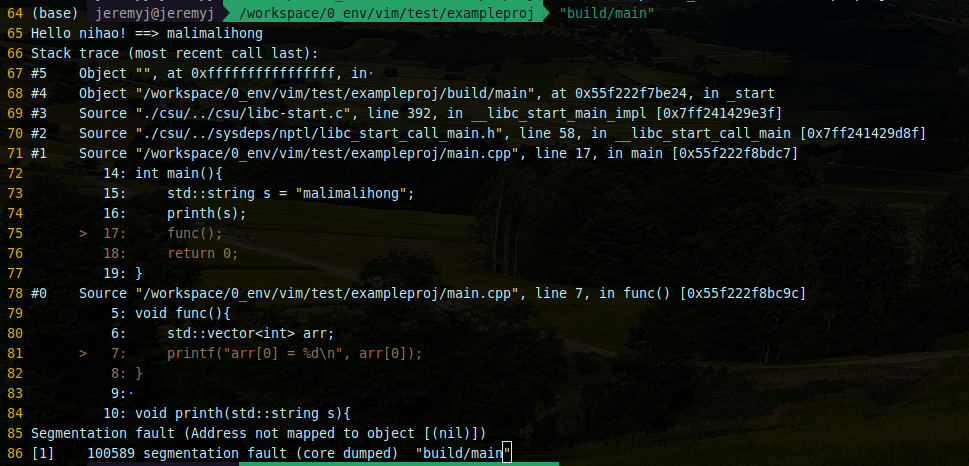
记录 | gdb使用backward-cpp来美化调试log
# 在当前工程目录下 git clone https://github.com/bombela/backward-cpp.git 编辑CMakeList.txt cmake_minimum_required(VERSION 3.15)project(exampleproj LANGUAGES CXX)add_subdirectory(backward-cpp)add_executable(main main.cpp)target_sources(main PUBLIC ${BACKW…...
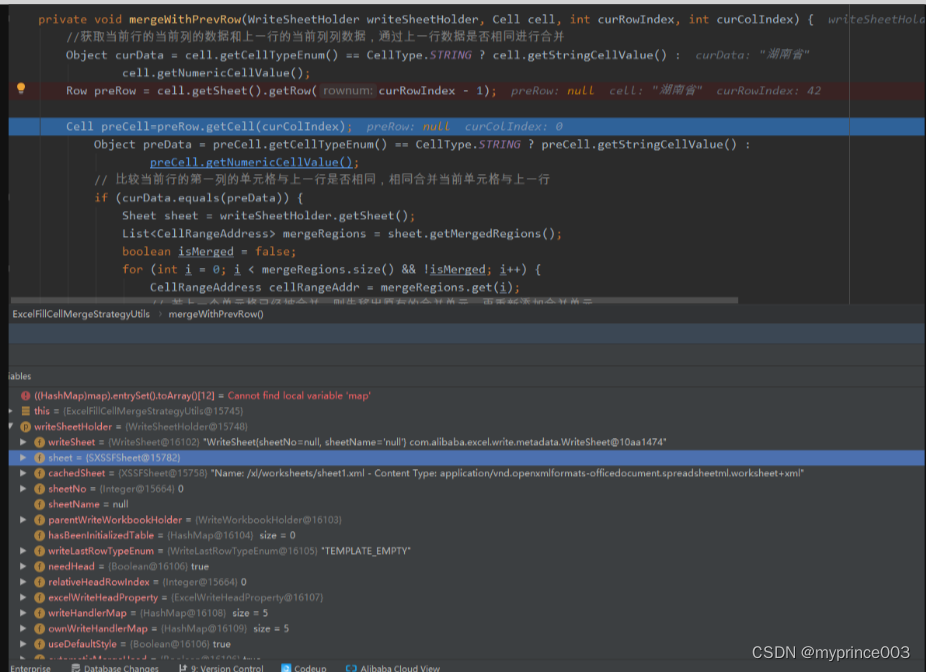
EasyExcel模板导出(行和列自动合并)
1.需求背景: ①需要从第三方获取数据,第三方接口有两个参数,开始时间和结束时间 ②获取回来的数据并没有入库,所以不能通过数据库将数据归类统计,excel合并大概的流程是判断上一行或者左右相邻列是否相同,然后进行合并,所以不能是零散的数据且客户要求每一个自治区和每一个航站…...

EOCR-i3MZ/iFMZ施耐德漏电保护继电器产品简介
EOCR-i3MZ/iFMZ是施耐德EOCR的新一代电子式电动机保护器产品,具有过电流、欠电流、缺相、逆相、堵转、失速、三相不平衡、接地等保护功能。EOCR-i3MZ/iFMZ是通讯型产品,提供Modbus RTU通讯协议,RS485接口。 为方便设备维护人员排查电动机的故…...

golang开发--beego入门
Beego 是一个基于 Go 语言的开源框架,用于构建 Web 应用程序和 API。它采用了一些常见的设计模式,以提高开发效率、代码可维护性和可扩展性。 一,MVC设计模式 Beego 框架采用了经典的 MVC(Model-View-Controller)设计…...

python调取一欧易API并写一个比特币均线交易策略
比特币均线交易策略是一种基于比特币价格的移动均线的交易策略。它通过计算不同时间段的移动均线来确定买入和卖出点。 具体步骤如下: 确定要使用的均线。常用的均线包括5日、10日、20日、50日和200日均线。较短的均线可以更快地反应价格变动,而较长的均…...

使用arthas排查请求超时问题
现象 客户端调用服务时间出现偶尔超时现象 排查 因为服务已开启arthas,使用trace命令监控 $ trace com.lizz slowfun #cost > 1000 -n 10 监控com.lizz类中的slowfun方法,输出用时超过1000ms的记录,记录10条 Press CtrlC to abort. Aff…...

SAP ABAP EXCEL 下载模板并导入
具体参考: ABAP EXCEL 下载摸板 获取数据模板文件路径 FORM fm_get_filepath .DATA: lv_filename TYPE string,lv_path TYPE string,lv_fullpath TYPE string,lv_title TYPE string.co_objid ZMMRP002.CONCATENATE co_objid - sy-datum sy-uzeit INTO l…...

Map集合体系
Map集合的概述 Map集合是一种双列集合,每个元素包含两个数据。 Map集合的每个元素的格式:keyvalue(键值对元素)。 Map集合也被称为“键值对集合”。 Map集合的完整格式:{key1value1 , key2value2 , key3value3 , ...} Map集合的使用场景…...

速度与稳定性的完美结合:深入横测ToDesk、TeamViewer和AnyDesk
文章目录 前言什么是远程办公?远程办公的优势 远程办公软件横测对象远程软件的注册&安装ToDeskTeamViewerAnyDesk 各场景下的实操体验1.办公文件传输及丢包率2.玩游戏操作延迟、稳定3.追剧画质流畅度、稳定4.临时技术支持SOS模式 收费情况与设备连接数总结 前言…...

数据库系统的结构
数据库系统的结构 1 数据抽象1.1 物理层1.2 逻辑层1.3 视图层 2 实例和模式3 数据独立性4 数据模型4.1 基于对象的逻辑模型4.2 基于记录的逻辑模型4.3 基于记录的物理模型 5 数据库语言5.1 数据定义语言 DDL5.2 数据操纵语言 DML 6 事务7 存储管理器8 数据库系统的总体结构 1 数…...

ngrok编译
ngrok编译 安装golang 官方golang安装文档:https://golang.google.cn/doc/install 配置国内源 go env -w GOPROXYhttps://goproxy.cn,direct关掉GO111MODULE go env -w GO111MODULEoff 配置访问github proxy_host$1 # 192.168.126.173 proxy_port$1 # 7890 exp…...

YOLOv5改进 | 卷积篇 | 通过RFAConv重塑空间注意力(深度学习的前沿突破)
一、本文介绍 本文给大家带来的改进机制是RFAConv,全称为Receptive-Field Attention Convolution,是一种全新的空间注意力机制。与传统的空间注意力方法相比,RFAConv能够更有效地处理图像中的细节和复杂模式(适用于所有的检测对象都有一定的…...

056:vue工具 --- CSS在线格式化
第056个 查看专栏目录: VUE ------ element UI 专栏目标 在vue和element UI联合技术栈的操控下,本专栏提供行之有效的源代码示例和信息点介绍,做到灵活运用。 (1)提供vue2的一些基本操作:安装、引用,模板使…...

自定义IDEA代码补全插件
目标: 对于项目中的静态方法(主要是各种工具类里的静态方法),可以在输入方法名时直接提示相关的静态方法,选中后自动补全代码,并导入静态类。 设计: 初步构想,用户选择要导入的文…...
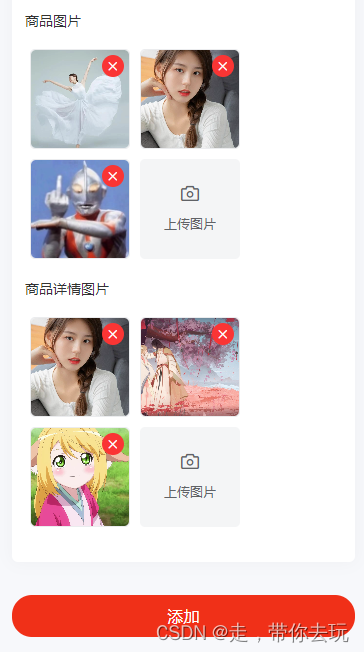
uniapp uview1.0 页面多个upload上传、回显之后处理数据
<view class"img-title w-s-color-3 f-28 row">商品图片</view><u-upload ref"images" :header"header" :file-list"fileListImages" :action"action" name"iFile" icon-name"camera"u…...
生活中的物理2——人类迷惑行为(用笔扎手)
1实验 材料 笔、手 实验 1、先用手轻轻碰一下笔尖(未成年人须家长监护) 2、再用另一只手碰碰笔尾 你发现了什么?? 2发现 你会发现碰笔尖的手明显比碰笔尾的手更痛 你想想为什么 3原理 压强f/s 笔尖的面积明显比笔尾的小 …...
vue3表格导入导出.xlsx
在这次使用时恰好整出来了,希望大家也能学习到,特此分享出来 使用前确保安装以下模块,最好全局配置element-plus ### 展示一下 ### ###导出选项 ### ###导入de数据 ### 安装的模块 npm install js-table2excel // 安装js-table2excel n…...
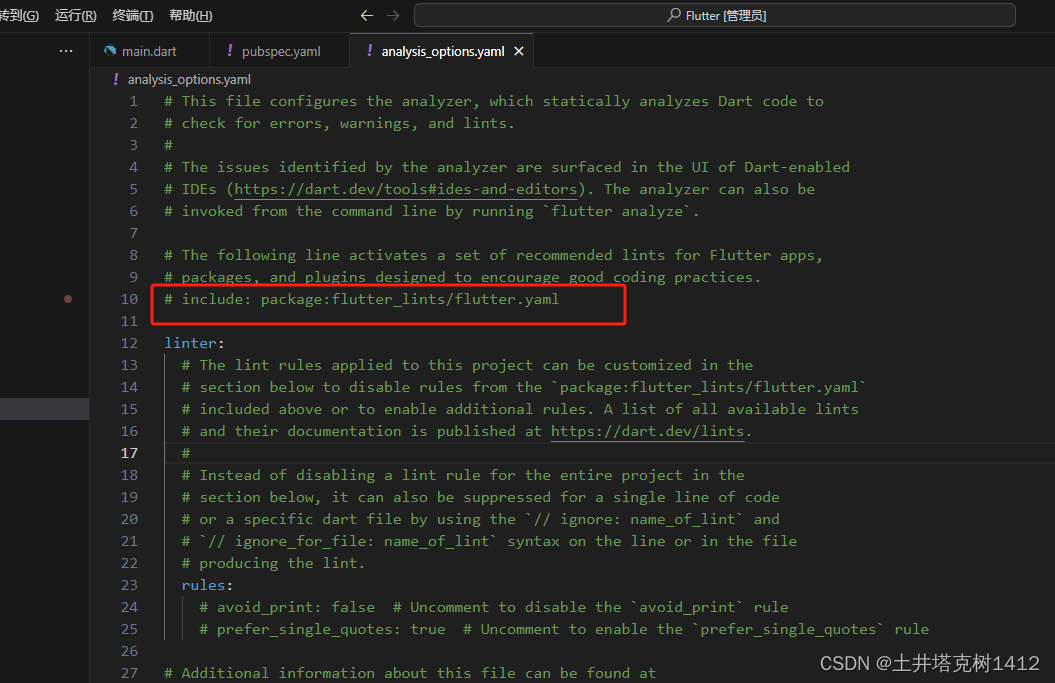
vscode dart语言出现蓝色波浪线
pubspec.yaml 注释掉:flutter_lints: ^2.0.0 analysis_options.yaml 注释掉:include: package:flutter_lints/flutter.yaml...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...
