智能优化算法应用:基于非洲秃鹫算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于非洲秃鹫算法3D无线传感器网络(WSN)覆盖优化 - 附代码
文章目录
- 智能优化算法应用:基于非洲秃鹫算法3D无线传感器网络(WSN)覆盖优化 - 附代码
- 1.无线传感网络节点模型
- 2.覆盖数学模型及分析
- 3.非洲秃鹫算法
- 4.实验参数设定
- 5.算法结果
- 6.参考文献
- 7.MATLAB代码
摘要:本文主要介绍如何用非洲秃鹫算法进行3D无线传感器网(WSN)覆盖优化。
1.无线传感网络节点模型
本文主要基于0/1模型,进行寻优。在二维平面上传感器节点的感知范围是一个以节点为圆心,半径为 R n R_n Rn的圆形区域,该圆形区域通常被称为该节点的“感知圆盘”, R n R_n Rn称为传感器节点的感知半径,感知半径与节点内置传感器件的物理特性有关,假设节点 n n n的位置坐标为 ( x n , y n , z n ) (x_n,y_n,z_n) (xn,yn,zn)在0-1感知模型中,对于平面上任意一点 p ( x p , y p , z p ) p(x_p,y_p,z_p) p(xp,yp,zp),则节点 n n n监测到区域内点 p p p的事件发生概率为:
P r ( n , p ) = { 1 , d ( n , p ) ≤ R n 0 , e s l e (1) P_r(n,p)=\begin{cases}1, \,d(n,p)\leq R_n\\ 0,\, esle \end{cases}\tag{1} Pr(n,p)={1,d(n,p)≤Rn0,esle(1)
其中 d ( n , p ) = ( x n − x p ) 2 + ( y n − y p ) 2 + ( z n − z p ) 2 d(n,p)=\sqrt{(x_n-x_p)^2+(y_n-y_p)^2 + (z_n-z_p)^2} d(n,p)=(xn−xp)2+(yn−yp)2+(zn−zp)2为点和之间的欧式距离。
2.覆盖数学模型及分析
现假定目标监测区域为二维平面,在区域 A r e a Area Area上投放同型结构传感器节点的数目为N,每个节点的位置坐标值假设已被初始化赋值,且节点的感知半径r。传感器节点集则表示为:
N o d e { x 1 , . . . , x N } (2) Node\{x_1,...,x_N\} \tag{2} Node{x1,...,xN}(2)
其中 n o d e i = { x i , y i , z i , r } node_i=\{x_i,y_i,z_i,r\} nodei={xi,yi,zi,r},表示以节点 ( x i , y i , z i ) (x_i,y_i,z_i) (xi,yi,zi)为圆心,r为监测半径的球,假定监测区域 A r e a Area Area被数字化离散为 m ∗ n ∗ l m*n*l m∗n∗l个空间点,空间点的坐标为 ( x , y , z ) (x,y,z) (x,y,z),目标点与传感器节点间的距离为:
d ( n o d e i , p ) = ( x i − x ) 2 + ( y i − y ) 2 + ( z i − z ) 2 (3) d(node_i,p)=\sqrt{(x_i-x)^2+(y_i-y)^2 + (z_i-z)^2}\tag{3} d(nodei,p)=(xi−x)2+(yi−y)2+(zi−z)2(3)
目标区域内点被传感器节点所覆盖的事件定义为 c i c_i ci。则该事件发生的概率 P c i P{c_i} Pci即为点 ( x , y , z ) (x,y,z) (x,y,z)被传感器节点 n o d e i node_i nodei所覆盖的概率:
P c o v ( x , y , z , n o d e i ) = { 1 , i f d ( n o d e i , p ) ≤ r 0 , e s l e (4) P_{cov}(x,y,z,node_i)=\begin{cases}1, if\,d(node_i,p)\leq r\\ 0,\, esle \end{cases}\tag{4} Pcov(x,y,z,nodei)={1,ifd(nodei,p)≤r0,esle(4)
我们将所有的传感器节点在目标监测环境中的区域覆盖率 C o v e r R a t i o CoverRatio CoverRatio定义为传感器节点集的覆盖面积与监测区域的面积之比,如公式所示:
C o v e r R a t i o = ∑ P c o v m ∗ n ∗ l (5) CoverRatio = \frac{\sum P_{cov}}{m*n*l}\tag{5} CoverRatio=m∗n∗l∑Pcov(5)
那我们的最终目标就是找到一组节点使得覆盖率最大。
3.非洲秃鹫算法
非洲秃鹫算法原理请参考:https://blog.csdn.net/u011835903/article/details/122213857
非洲秃鹫算法是寻找最小值。于是适应度函数定义为未覆盖率最小,即覆盖率最大。如下:
f u n = a r g m i n ( 1 − C o v e r R a t i o ) = a r g m i n ( 1 − ∑ P c o v m ∗ n ∗ l ) (6) fun = argmin(1 - CoverRatio) = argmin(1-\frac{\sum P_{cov}}{m*n*l}) \tag{6} fun=argmin(1−CoverRatio)=argmin(1−m∗n∗l∑Pcov)(6)
4.实验参数设定
无线传感器覆盖参数设定如下:
%% 设定WNS覆盖参数,
%% 默认输入参数都是整数,如果想定义小数,请自行乘以系数变为整数再做转换。
%% 比如范围1*1,R=0.03可以转换为100*100,R=3;
%区域范围为AreaX*AreaY*AreaZ
AreaX = 100;
AreaY = 100;
AreaZ = 100;
N = 20 ;%覆盖节点数
R = 15;%通信半径非洲秃鹫算法参数如下:
%% 设定非洲秃鹫优化参数
pop=30; % 种群数量
Max_iteration=30; %设定最大迭代次数
lb = ones(1,3*N);
ub = [AreaX.*ones(1,N),AreaY.*ones(1,N),AreaZ.*ones(1,N)];
dim = 3*N;%维度为3N,N个坐标点
5.算法结果


从结果来看,覆盖率在优化过程中不断上升。表明非洲秃鹫算法对覆盖优化起到了优化的作用。
6.参考文献
[1] 史朝亚. 基于PSO算法无线传感器网络覆盖优化的研究[D]. 南京理工大学.
7.MATLAB代码
相关文章:

智能优化算法应用:基于非洲秃鹫算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于非洲秃鹫算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于非洲秃鹫算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.非洲秃鹫算法4.实验参数设定5.算法结果6.…...
持续集成交付CICD:Jenkins使用GitLab共享库实现前端项目镜像构建
目录 一、实验 1. GitLab修改项目文件与Harbor环境确认 2.Jenkins使用GitLab共享库实现前端项目镜像构建 3.优化CI流水线封装Harbor账户密码 4.Jenkins再次使用GitLab共享库实现前端项目镜像构建 一、实验 1. GitLab修改项目文件与Harbor环境确认 (1…...

SQL server 数据库 SQL语句高级用法
1、表的高级查询 use student select * from stuinfo1 -- 使用 in 的子查询 select * from stuinfo where stu_age in ( select stu_age from stuinfo where cla_id 12345 ) select * from stuinfo where stu_age in ( 19 , 20 , 21 , 25 , 23 , 1…...

wavlink 路由器 多处前台RCE漏洞复现
0x01 产品简介 WAVLINK是中国睿因科技(WAVLINK)公司开发的一款路由器。 0x02 漏洞概述 WAVLINK路由器mesh.cgi、nightled.cgi、live-api.cgi等接口处存在命令执行漏洞,攻击者可通过该漏洞获取服务器权限。包含型号WN530HG4、WN531G3、WN572HG3、WN535G3、WN575A4等。 0x…...

互联网中的商品超卖问题及其解决方案:Java中Redis结合UUID的应用
前言 在设计商品下单和库存扣减,你一定遇到过这样的问题,库存扣减为0了,可是消费者还能下单,并将订单信息保存到了数据库里,针对商品超卖问题,作此篇以解决。 随着互联网商业的飞速发展,商品超…...
mysql:查看线程缓存中的线程数量
使用命令show global status like Threads_cached;可以查看线程缓存中的线程数量。 例如,查询线程缓存中的线程数量如下: 然后启动应用程序,使用连接,查询如下: 由查询结果可以看到,线程缓存中的线程数量…...
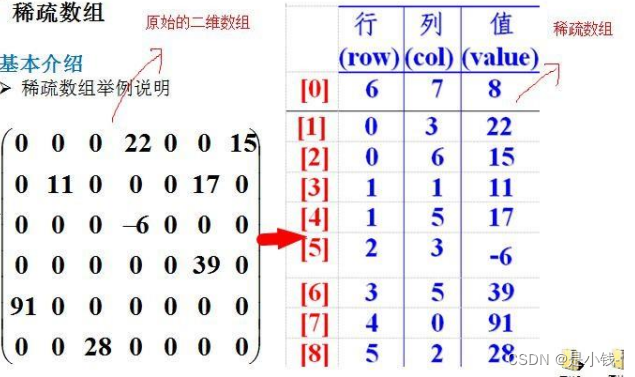
线性表,也是Java中数组的知识点!
线性表定义: 由n (n≥0)个数据特性相同的元素构成的有限序列称为线性表,(n0)的时候被称为空表。 线性表的顺序表示 线性表的顺序存储又被称为顺序表 优点 无需为表示表中元素之间的逻辑关系而增加额外的存储空间可以随意读取任意位置的元素 缺点 插入…...

java使用面向对象实现图书管理系统
꒰˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱ ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客 本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN …...

2023 英特尔On技术创新大会直播 |我感受到的“芯”魅力
文章目录 每日一句正能量前言AI时代,云与PC结合为用户带来更好体验全新处理器,首次引入针对人工智能加速的NPU大模型时代,软硬结合带来更好训练成果后记 每日一句正能量 成长是一条必走的路路上我们伤痛在所难免。 前言 在2023年的英特尔On技…...
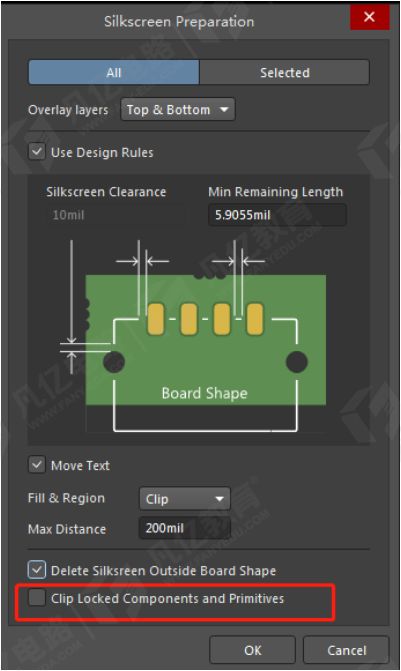
Atium Designer 23 全新功能-丝印制备,解决DFM问题
进行PCB设计时需要养成良好的设计习惯,才能保证后期的生产效果。例如整板上需要保证丝印跟阻焊的间距规则避免产生丝印重叠造成的PCB制造设计(DFM)问题。丝印重叠阻焊的影响有如下: 1)PCB板后期打样,一般是…...
Nginx快速入门:安装目录结构详解及核心配置解读(二)
0. 引言 上节我们讲解了nginx的应用场景和安装,本节继续针对nginx的各个目录文件进行讲解,让大家更加深入的认识nginx。并通过一个实操案例,带大家来实际认知nginx的核心配置 1. nginx安装目录结构 首先nginx的默认安装目录为:…...

测试TensorFlow/PyTorch的GPU版本是否启用
文章目录 1. Pytorch测试代码2. TensorFlow测试代码 后续遇到好的会不断更新。。。 1. Pytorch测试代码 import torch def gpu_is_available():print(\nGPU details:)print(f gpu_is_available : , torch.cuda.is_available())print(f cuda_device_count : , t…...
字符串逆序输出
逆序输出就是本来abc输出的,然后我想让他输出成cba,那么我们还是要用到for循环,只不过原先是从零开始往上加,这回呢,是从上面往下减 我们观察上面这个图片,我们想要输出olleh,那么我们就要从4开…...

期货平仓日历(期货平仓日期汇总)
什么是期货平仓日历? 期货是一种高风险高收益的投资品种。而期货交易不同于股票等其他投资品种的交易,期货交易需要在一定时间内才能买卖。而期货平仓日历就是指期货交易中规定的所有合约的平仓日期汇总。 常见期货平仓日期和时间? 不同的…...
计算机网络-进阶
目录 易混淆物理层数据链路层网络层nat如何实现私有ip通信IP数据报 格式解析tcp 连接tcp流量控制滑动窗口拥塞控制 报文捕获 wireshark路由模拟器 enspcdn代理服务器 VS cdn VS web cache 计算机有了物理地址,为什么还要有ip地址?单播 多播 广播 传输层会…...
LED恒流驱动芯片SM2188EN:满足LED灯具出口欧盟所需的ERP能效认证标准和要求
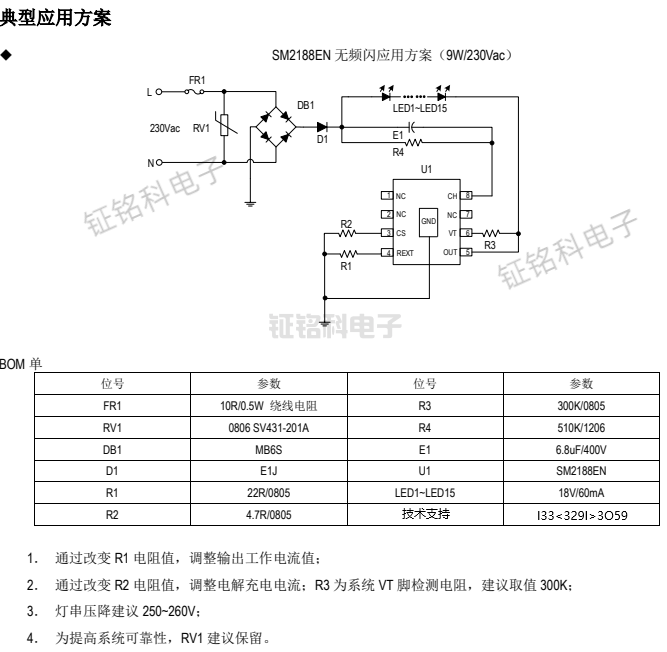
LED灯具是一种节能环保的照明产品,因其高效节能、长寿命等优点而备受消费者青睐,成为照明市场的主流产品。作为LED灯具出口欧盟市场的必备条件,ERP能效认证标准和要求对LED灯具的能效性能提出了严格的要求。 首先,ERP能效认证标准…...

RocketMQ系统性学习-RocketMQ原理分析之消费者的接收消息流程
🌈🌈🌈🌈🌈🌈🌈🌈 【11来了】文章导读地址:点击查看文章导读! 🍁🍁🍁🍁🍁🍁dz…...

butterfly蝴蝶分类
一、分类原因 由于植物分类所使用的数据集存在一定问题,修改起来比较麻烦,本次采用kaggle的ButterflyMothsImageClassification数据集,对100这种蝴蝶进行分类。 二、100中蝴蝶类别 ‘ADONIS’,‘AFRICAN GIANT SWALLOWTAIL’,‘AMERICAN S…...

计算机基础:网络基础
目录 一.网线制作 1.制作所需要工具 网线制作标准 编辑 2.水晶头使用 3.网线钳使用 4.视频教学 二.集线器、交换机介绍 1.OSI七层模型 2.TCP/IP四层参考模型 3.集线器、交换机。路由器介绍 集线器 交换机 路由器 区别 三.路由器的配置 1.路由器设置 说明书 设…...

[原创][R语言]股票分析实战[3]:周级别涨幅趋势的相关性
[简介] 常用网名: 猪头三 出生日期: 1981.XX.XX QQ联系: 643439947 个人网站: 80x86汇编小站 https://www.x86asm.org 编程生涯: 2001年~至今[共22年] 职业生涯: 20年 开发语言: C/C、80x86ASM、PHP、Perl、Objective-C、Object Pascal、C#、Python 开发工具: Visual Studio、D…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...
