二叉树题目:输出二叉树
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 前言
- 解法一
- 思路和算法
- 代码
- 复杂度分析
- 解法二
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:输出二叉树
出处:655. 输出二叉树
难度
6 级
题目描述
要求
给定二叉树的根结点 root \texttt{root} root,创建 m × n \texttt{m} \times \texttt{n} m×n 的字符串矩阵 res \texttt{res} res 表示二叉树的格式化输出。格式化输出矩阵应根据以下规则创建:
- 树的高度是 height \texttt{height} height,行数 m \texttt{m} m 应等于 height + 1 \texttt{height} + \texttt{1} height+1。
- 列数 n \texttt{n} n 应等于 2 height + 1 − 1 \texttt{2}^{\texttt{height} + \texttt{1}} - \texttt{1} 2height+1−1。
- 根结点放置在第一行的正中间(更正式而言,位于 res[0][(n - 1) / 2] \texttt{res[0][(n - 1) / 2]} res[0][(n - 1) / 2])。
- 对于每个放置在矩阵中 res[r][c] \texttt{res[r][c]} res[r][c] 位置的结点,将其左子结点放置在 res[r + 1][c − 2 height − r − 1 ] \texttt{res[r} + \texttt{1][c} - \texttt{2}^{\texttt{height} - \texttt{r} - \texttt{1}}\texttt{]} res[r+1][c−2height−r−1],右子结点放置在 res[r + 1][c + 2 height − r − 1 ] \texttt{res[r} + \texttt{1][c} + \texttt{2}^{\texttt{height} - \texttt{r} - \texttt{1}}\texttt{]} res[r+1][c+2height−r−1]。
- 重复该过程,直到所有结点都放置到矩阵中。
- 所有空单元格应包含空字符串 "" \texttt{""} ""。
返回创建的矩阵 res \texttt{res} res。
示例
示例 1:
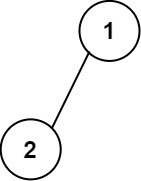
输入: root = [1,2] \texttt{root = [1,2]} root = [1,2]
输出:
[["", "1", ""], \texttt{[["", "1", ""],} [["", "1", ""],
["2", "", ""]] \texttt{ ["2", "", ""]]} ["2", "", ""]]
示例 2:
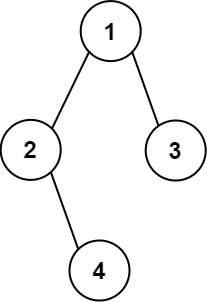
输入: root = [1,2,3,null,4] \texttt{root = [1,2,3,null,4]} root = [1,2,3,null,4]
输出:
[["", "", "", "1", "", "", ""], \texttt{[["", "", "", "1", "", "", ""],} [["", "", "", "1", "", "", ""],
["", "2", "", "", "", "3", ""], \texttt{ ["", "2", "", "", "", "3", ""],} ["", "2", "", "", "", "3", ""],
["", "", "4", "", "", "", ""]] \texttt{ ["", "", "4", "", "", "", ""]]} ["", "", "4", "", "", "", ""]]
数据范围
- 树中结点数目在范围 [1, 2 10 ] \texttt{[1, 2}^\texttt{10}\texttt{]} [1, 210] 内
- -99 ≤ Node.val ≤ 99 \texttt{-99} \le \texttt{Node.val} \le \texttt{99} -99≤Node.val≤99
- 树的高度在范围 [1, 10] \texttt{[1, 10]} [1, 10] 内
前言
这道题要求将给定的二叉树格式化输出,使用矩阵表示格式化输出的结果。由于矩阵的行数和列数由二叉树的高度决定,因此需要首先计算二叉树的高度,根据二叉树的高度计算矩阵的行数和列数,创建矩阵之后遍历二叉树并将每个结点值填入矩阵中的对应位置。
计算二叉树的高度可以使用「二叉树的最大深度」的做法,使用深度优先搜索或者广度优先搜索得到二叉树的高度。这道题中定义的二叉树的高度为从根结点到最远叶结点的路径上的边数,因此边界情况为只有一个结点的二叉树的高度是 0 0 0。
得到二叉树的高度 height \textit{height} height 之后,即可得到矩阵的行数 m = height + 1 m = \textit{height} + 1 m=height+1,列数 n = 2 m − 1 n = 2^m - 1 n=2m−1。创建矩阵之后,首先将根结点值填入矩阵的第 0 0 0 行第 n − 1 2 \dfrac{n - 1}{2} 2n−1 列,然后遍历二叉树的其余结点并填入矩阵中的对应位置。
当一个结点的位置确定之后,可以根据该结点在矩阵中的行列下标以及二叉树的高度决定其子结点的位置。如果一个结点位于第 row \textit{row} row 行第 column \textit{column} column 列,则其左子结点位于第 row + 1 \textit{row} + 1 row+1 行第 column − 2 height − row − 1 \textit{column} - 2^{\textit{height} - \textit{row} - 1} column−2height−row−1 列,其右子结点位于第 row + 1 \textit{row} + 1 row+1 行第 column + 2 height − row − 1 \textit{column} + 2^{\textit{height} - \textit{row} - 1} column+2height−row−1 列。
输出二叉树可以使用深度优先搜索或者广度优先搜索实现。
解法一
思路和算法
使用深度优先搜索输出二叉树时,首先将根结点值填入矩阵的第 0 0 0 行第 n − 1 2 \dfrac{n - 1}{2} 2n−1 列,然后计算出非空子结点在矩阵中的位置,继续遍历非空子树并将其余的结点值填入矩阵,直到所有结点遍历完毕,此时所有结点值都填入矩阵中的对应位置。
整个过程是一个递归的过程,递归的终止条件是当前结点为叶结点,此时将当前结点值填入矩阵中的对应位置,然后直接返回。对于其余情况,在将当前结点值填入矩阵中的对应位置之后,对非空子结点执行递归。
代码
class Solution {List<List<String>> res = new ArrayList<List<String>>();int height;public List<List<String>> printTree(TreeNode root) {height = getHeight(root);int m = height + 1;int n = (1 << m) - 1;for (int i = 0; i < m; i++) {List<String> row = new ArrayList<String>();for (int j = 0; j < n; j++) {row.add("");}res.add(row);}dfs(root, 0, (n - 1) / 2);return res;}public int getHeight(TreeNode root) {TreeNode left = root.left, right = root.right;if (left == null && right == null) {return 0;}int leftHeight = left != null ? getHeight(left) : -1;int rightHeight = right != null ? getHeight(right) : -1;return Math.max(leftHeight, rightHeight) + 1;}public void dfs(TreeNode node, int row, int column) {res.get(row).set(column, String.valueOf(node.val));TreeNode left = node.left, right = node.right;if (left != null) {dfs(left, row + 1, column - (1 << (height - row - 1)));}if (right != null) {dfs(right, row + 1, column + (1 << (height - row - 1)));}}
}
复杂度分析
-
时间复杂度: O ( h × 2 h ) O(h \times 2^h) O(h×2h),其中 h h h 是二叉树的高度。矩阵的行数 m m m 和列数 n n n 满足 m = h + 1 m = h + 1 m=h+1, n = 2 h + 1 − 1 n = 2^{h + 1} - 1 n=2h+1−1,输出二叉树的时间复杂度是 O ( m n ) = O ( h × 2 h ) O(mn) = O(h \times 2^h) O(mn)=O(h×2h)。
-
空间复杂度: O ( h ) O(h) O(h),其中 h h h 是二叉树的高度。空间复杂度主要是递归调用的栈空间,取决于二叉树的高度。注意返回值不计入空间复杂度。
解法二
思路和算法
使用广度优先搜索输出二叉树时,使用两个队列分别存储待访问的结点和结点在矩阵中的位置,两个队列分别为结点队列和位置队列。初始时,将根结点入结点队列,将第 0 0 0 行第 n − 1 2 \dfrac{n - 1}{2} 2n−1 列入位置队列。
每次将一个结点从结点队列出队,并将一个位置从位置队列出队,出队的位置即为出队的结点在矩阵中的位置。将当前结点值填入矩阵中的对应位置,然后计算出非空子结点在矩阵中的位置,将非空子结点和对应位置分别入两个队列。重复该过程直到所有结点遍历完毕,此时所有结点值都填入矩阵中的对应位置。
代码
class Solution {public List<List<String>> printTree(TreeNode root) {int height = getHeight(root);int m = height + 1;int n = (1 << m) - 1;List<List<String>> res = new ArrayList<List<String>>();for (int i = 0; i < m; i++) {List<String> row = new ArrayList<String>();for (int j = 0; j < n; j++) {row.add("");}res.add(row);}Queue<TreeNode> nodeQueue = new ArrayDeque<TreeNode>();Queue<int[]> locationQueue = new ArrayDeque<int[]>();nodeQueue.offer(root);locationQueue.offer(new int[]{0, (n - 1) / 2});while (!nodeQueue.isEmpty()) {TreeNode node = nodeQueue.poll();int[] location = locationQueue.poll();int row = location[0], column = location[1];res.get(row).set(column, String.valueOf(node.val));TreeNode left = node.left, right = node.right;if (left != null) {nodeQueue.offer(left);locationQueue.offer(new int[]{row + 1, column - (1 << (height - row - 1))});}if (right != null) {nodeQueue.offer(right);locationQueue.offer(new int[]{row + 1, column + (1 << (height - row - 1))});}}return res;}public int getHeight(TreeNode root) {int depth = -1;Queue<TreeNode> queue = new ArrayDeque<TreeNode>();queue.offer(root);while (!queue.isEmpty()) {depth++;int size = queue.size();for (int i = 0; i < size; i++) {TreeNode node = queue.poll();if (node.left != null) {queue.offer(node.left);}if (node.right != null) {queue.offer(node.right);}}}return depth;}
}
复杂度分析
-
时间复杂度: O ( h × 2 h ) O(h \times 2^h) O(h×2h),其中 h h h 是二叉树的高度。矩阵的行数 m m m 和列数 n n n 满足 m = h + 1 m = h + 1 m=h+1, n = 2 h + 1 − 1 n = 2^{h + 1} - 1 n=2h+1−1,输出二叉树的时间复杂度是 O ( m n ) = O ( h × 2 h ) O(mn) = O(h \times 2^h) O(mn)=O(h×2h)。
-
空间复杂度: O ( 2 h ) O(2^h) O(2h),其中 h h h 是二叉树的高度。空间复杂度主要是队列空间,队列内元素个数不超过二叉树的结点数,高度为 h h h 的二叉树中最多有 2 h + 1 − 1 2^{h + 1} - 1 2h+1−1 个结点。注意返回值不计入空间复杂度。
相关文章:

二叉树题目:输出二叉树
文章目录 题目标题和出处难度题目描述要求示例数据范围 前言解法一思路和算法代码复杂度分析 解法二思路和算法代码复杂度分析 题目 标题和出处 标题:输出二叉树 出处:655. 输出二叉树 难度 6 级 题目描述 要求 给定二叉树的根结点 root \textt…...

apache poi_5.2.5 实现对表格单元格的自定义变量名进行图片替换
apache poi_5.2.5 实现对表格单元格的自定义变量名进行图片替换 实现思路 1.首先定位到自定义变量名 2.然后先清除自定义变量名,可利用setText(null,0)来清除 3.在自定义变量名的位置添加图片,使用下面的代码 4.对于图片布局有要求的,利用C…...
Kafka--Kafka日志索引详解以及生产常见问题分析与总结
一、Kafka的Log日志梳理 这一部分数据主要包含当前Broker节点的消息数据(在Kafka中称为Log日志)。这是一部分无状态的数据,也就是说每个Kafka的Broker节点都是以相同的逻辑运行。这种无状态的服务设计让Kafka集群能够比较容易的进行水平扩展。比如你需要用一个新…...

Vue3-23-组件-依赖注入的使用详解
什么是依赖注入 个人的理解 : 依赖注入,是在 一颗 组件树中,由 【前代组件】 给 【后代组件】 提供 属性值的 一种方式 ;这种方式 突破了 【父子组件】之间通过 props 的方式传值的限制,只要是 【前代组件】提供的 依…...

css 美化滚动条
当div内容溢出容器定义的高度时,滚动条显示,并美化默认的滚动条样式 div 容器 <divclass"content">内容 </div>css 样式 /* 问话区域 滚动条 */ .content {overflow: auto;height: 662px;padding: 25px;scrollbar-width: thin; /* 设置滚动条宽度 */bo…...

Tomcat介绍及使用:构建强大的Java Web应用服务器
引言: 在现代软件开发中,Web应用已经成为了不可或缺的一部分。而为了构建高效、稳定的Web应用服务器,选择合适的工具和技术至关重要。Tomcat作为一款开源的Java Web应用服务器,凭借其丰富的功能和灵活的配置,成为了开发…...
怎么定义一套完成标准的JAVA枚举类型
一、背景 在java代码中,接口返回有各种各样的状态,比如400 401 200 500 403等常见的http状态码,也有我们自定义的很多业务状态码。如果系统比较复杂,制定一套完整的标准的状态码是非常有必要的,这样比较方面BUG排查。…...
Apache Seatunnel本地源码构建编译运行调试
Apache Seatunnel本地源码构建编译运行调试 文章目录 1. 环境准备1.1 Java环境1.2 Maven1.3 IDEA1.4 Docker环境1.5 Mysql8.0.281.6 其它环境准备 2. 源码包下载3. idea项目配置3.1 项目导入3.2 maven配置3.3 项目JDK配置3.4 项目启动参数配置3.4.1 seatunnel项目启动参数配置3…...
构建高效持久层:深度解析 MyBatis-Plus(02)
目录 引言1. 逻辑删除1.1 概述1.2 逻辑删除的优势1.3.为什么使用逻辑删除1.4 综合案例 2. 乐观锁和悲观锁2.1.什么是乐观锁和悲观锁2.2.乐观锁和悲观锁的区别2.3.综合案例 3. 分页插件总结 引言 在现代软件开发中,数据库操作是不可或缺的一环。为了提高系统的性能、…...
Gitlab仓库推送到Gitee仓库的一种思路
文章目录 Gitlab仓库推送到Gitee仓库的一种思路1、创建Gitee的ssh公钥(默认已有Gitlab的ssh公钥)2、添加Gitlab远程仓库地址3、添加Gitee远程仓库地址4、拉取Gitlab远程仓库指定分支到本地仓库指定分支(以test分支为例)5、推送本地…...
快速能访问服务器的文件
1、背景 访问ubuntu上的文件 2、方法 python3 -m http.server 8081 --directory /home/ NAS 共享访问协议 — NFS、SMB、FTP、WebDAV 各有何优势?http://1 Ubuntu 搭建文件服务器(Nginx)...
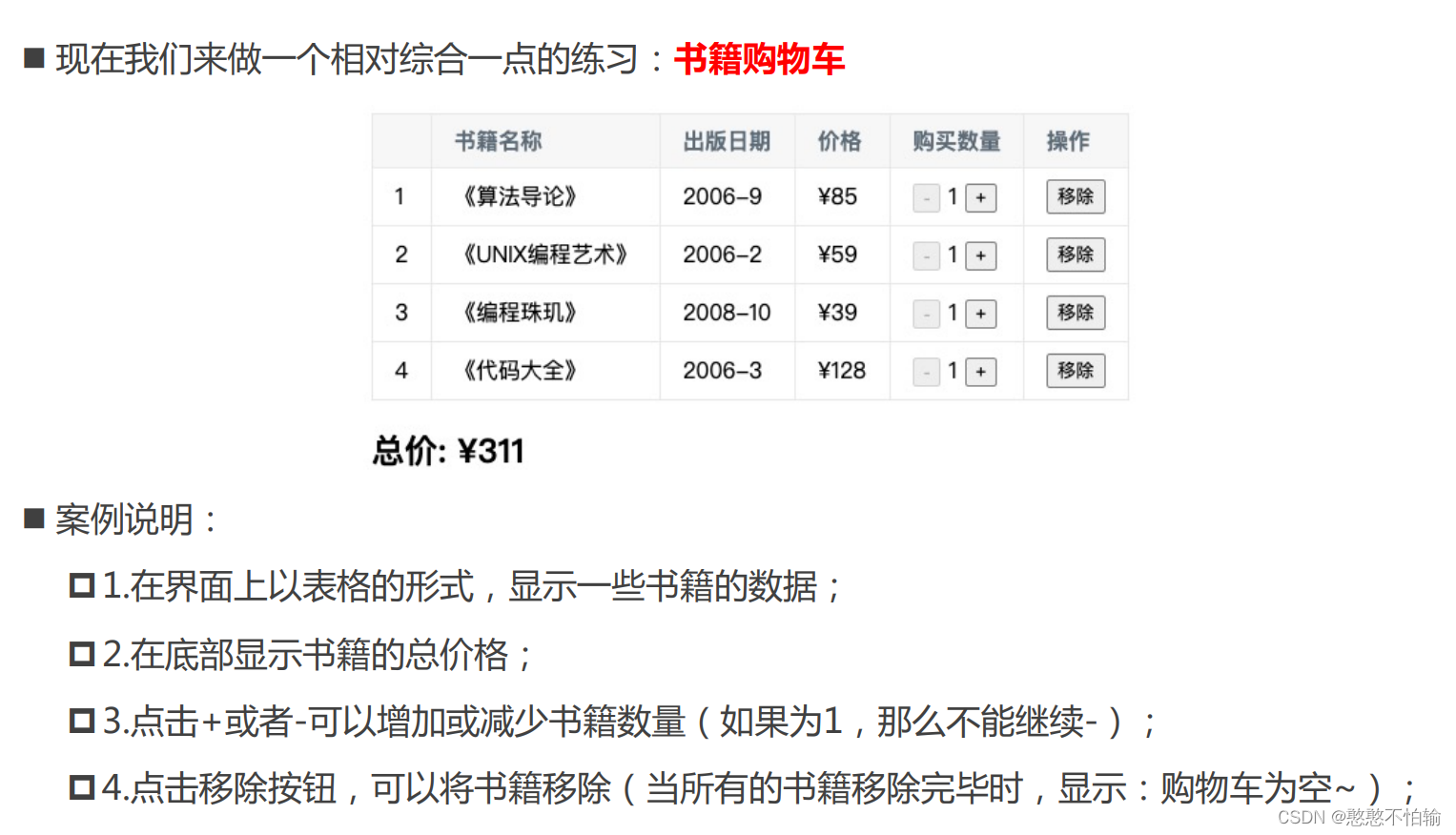
Diary26-Vue综合案例1-书籍购物车
Vue综合案例1-书籍购物车 案例要求: 代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewpor…...
【EasyExcel实践】万能导出,一个接口导出多张表以及任意字段(可指定字段顺序)-简化升级版
文章目录 前言正文一、项目简介二、核心代码2.1 pom.xml 依赖配置2.2 ExcelHeadMapFactory2.3 ExcelDataLinkedHashMap2.4 自定义注解 ExcelExportBean2.5 自定义注解 ExcelColumnTitle2.6 建造器接口 Builder2.7 表格工具类 ExcelUtils2.8 GsonUtil2.9 模版类 ExportDynamicCo…...
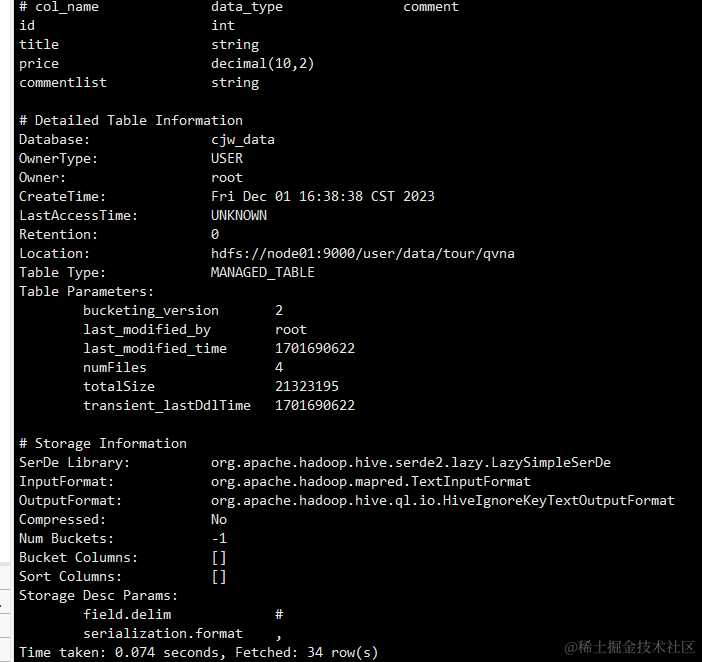
解决 Hive 外部表分隔符问题的实用指南
简介: 在使用 Hive 外部表时,分隔符设置不当可能导致数据导入和查询过程中的问题。本文将详细介绍如何解决在 Hive 外部表中正确设置分隔符的步骤。 问题描述: 在使用Hive外部表时,可能会遇到分隔符问题。这主要是因为Hive在读…...

一文学会 Apache Zeppelin
Zeppelin资料 Zeppelin项目信息 Zeppelin官网 http://zeppelin.apache.org/Zeppelin源码地址 https://github.com/apache/zeppelinZeppelin JIRA: https://issues.apache.org/jira/projects/ZEPPELIN/summaryZeppelin文档 Flink on Zeppelin 文档集中地 https://www.yuque.co…...
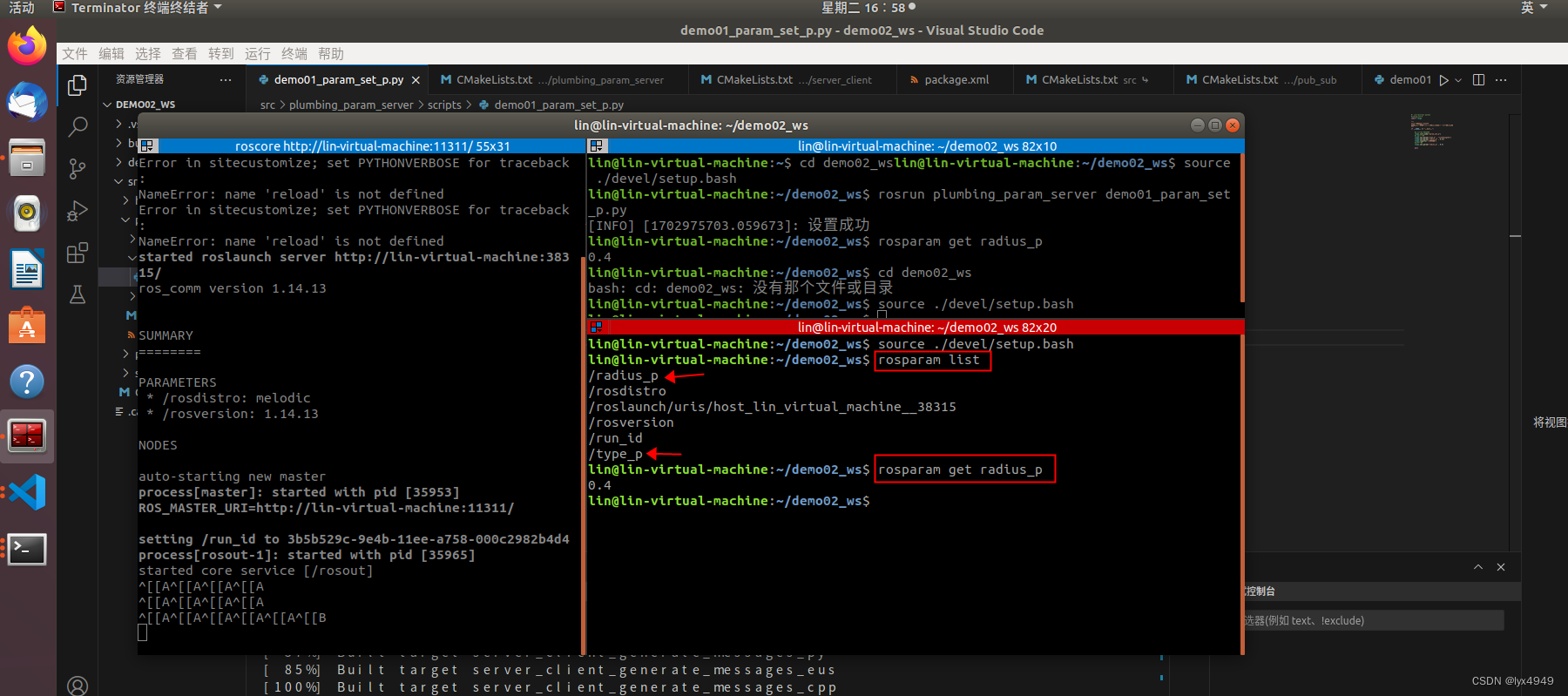
ROS学习笔记(七)---参数服务器
ROS学习笔记文章目录 01. ROS学习笔记(一)—Linux安装VScode 02. ROS学习笔记(二)—使用 VScode 开发 ROS 的Python程序(简例) 03. ROS学习笔记(三)—好用的终端Terminator 04. ROS学习笔记(四)—使用 VScode 启动launch文件运行多个节点 05. ROS学习笔…...

【RTOS学习】源码分析(信号量和互斥量 事件组 任务通知)
🐱作者:一只大喵咪1201 🐱专栏:《RTOS学习》 🔥格言:你只管努力,剩下的交给时间! 目录 🍓信号量和互斥量🍅创建🍅Take🍅Give &#x…...
 代码+解析)
1316:【例4.6】数的计数(Noip2001) 代码+解析
1316:【例4.6】数的计数(Noip2001) 【题目描述】 我们要求找出具有下列性质数的个数(包括输入的自然数n )。先输入一个自然数n(n≤1000),然后对此自然数按照如下方法进行处理:不作任何处理;在它的左边加上一…...

征集倒计时 | 2023年卓越影响力榜单-第四届中国产业创新奖报名即将截止
第四届「ISIG中国产业智能大会」将于2024年3月16日在上海举办。2024 ISIG 以“与科技共赢,与产业共进”为主题,共设立RPA超自动化、 低代码、AIGC大模型、流程挖掘四大主题峰会。届时,大会组委会将颁发2023年度卓越影响力榜单—第四届中国产业…...

vue的语法模板与数据绑定的说明
vue的两大模板语法: 1.插值语法 2.指定语法 插值语法:{{}} 功能:用于解析标签体的内容 写法:{{xxx}},xxx是js表达式,且可以直接读取到data中的所有属性 指定语法: 功能:用于解析标签(包括:标签属性、标…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
