当前位置： 首页 > news >正文

德人合科技 | 防止公司电脑文件数据资料外泄，自动智能透明加密保护系统

news 2026/2/10 0:12:40

【透明加密软件】——防止公司电脑文件数据资料防止外泄，自动智能透明加密保护内部核心文件、文档、图纸、源代码、音视频等资料！

PC端访问地址：

www.drhchina.com

🌟 核心功能：

透明加密：采用高级加密算法，对您的文件进行实时、透明的加密，确保数据安全。
权限控制：根据用户角色和需求，设定不同的访问权限，防止数据泄露。
审计追踪：详细记录用户的操作行为，便于事后审计和追踪。
跨平台支持：支持Windows、macOS、Linux等主流操作系统，满足您的多样化需求。

💡 产品优势：

高效稳定：采用先进的加密技术，确保加密过程高效、稳定，不占用系统资源。
易于使用：简洁直观的操作界面，让您轻松上手，无需额外培训。
兼容性强：兼容各类应用软件，不影响您的日常工作流程。
优质服务：提供7*24小时技术支持，为您解决任何疑问和问题。

移动端访问地址：

https://aisite.wejianzhan.com/site/wjz012xr/971c4604-0613-4200-bbcb-1e72f43c19ef

📜 适用场景：

企业办公：保护企业内部机密文件，防止泄露和窃取。
金融行业：保障客户信息和交易数据的安全。
政府部门：确保政务数据的安全和保密。
科研机构：保护知识产权和研究成果的安全。

相关文章：

德人合科技 | 防止公司电脑文件数据资料外泄，自动智能透明加密保护系统

【透明加密软件】——防止公司电脑文件数据资料防止外泄，自动智能透明加密保护内部核心文件、文档、图纸、源代码、音视频等资料！ PC端访问地址： www.drhchina.com 🌟 核心功能： 透明加密：采用高级加密算…...

编程日记 2023/12/21 21:38:32

常见加解密算法分析（含使用场景）

加密算法主要分为三类：对称加密算法、非对称加密算法和散列算法。下面将分别介绍这些类别中的常见算法及其特点和使用场景。 对称加密算法 1. AES (Advanced Encryption Standard) 简介： AES是一种广泛使用的对称加密标准，可以使用128、19…...

编程日记 2023/12/21 21:37:31

Oracle基本的SQL语句

1.最基本的增删改查 1.1.新增 insert 1.1.1.单表新增 INSERT INTO table_count_output (data_date,table_name,table_count ) VALUES (2023-03-15,FMCUSLVL,351 );COMMIT; 1.1.2.关联新增 INSERT INTO table_count_output (data_date,table_name,table_count )SELECTdata_…...

编程日记 2023/12/21 21:36:30

golang项目目录推荐

序言 逛GitHub的时候发现有个4.5k对goalng项目结构的推荐的项目，这里就简单的推荐下 文件目录 /cmd 项目主要的应用程序。 对于每个应用程序来说这个目录的名字应该和项目可执行文件的名字相匹（例如，/cmd/myapp）。不要在这个…...

编程日记 2023/12/21 21:35:30

Maven scope属性解读和使用注意事项

目录 compile runtime test system provided import dependencyManagement标签介绍 maven的scope有哪些&#xff1a; maven的scope一共包括&#xff1a;compile、runtime、test、system、provided、import。 compile <dependency><groupId>org.apache.htt…...

编程日记 2023/12/21 21:33:28

Vue3使用 xx UI解决布局高度自适应

解决方案 在相应的Sider部分添加&#xff1a;height: ‘91.8vh’&#xff0c;即可。示例&#xff1a; <Layout><Sider hide-trigger :style"{background: #fff, height: 91.8vh}"> }知识补充 vw、vh、vmin、vmax是一种视窗单位&#xff0c;也是相对单…...

编程日记 2023/12/21 21:27:23

九牧：科技卫浴，长期主义

“没有做错什么&#xff0c;但却输给了时代”&#xff0c;这是人们给当年手机巨头诺基亚的注解。 谁也没有想到&#xff0c;曾在手机行业称雄的诺基亚&#xff0c;最终败给了时代。当年&#xff0c;在2G向3G、4G跨越的时候&#xff0c;苹果、微软的iOS和安卓系统将手机从简单的…...

编程日记 2023/12/21 21:26:22

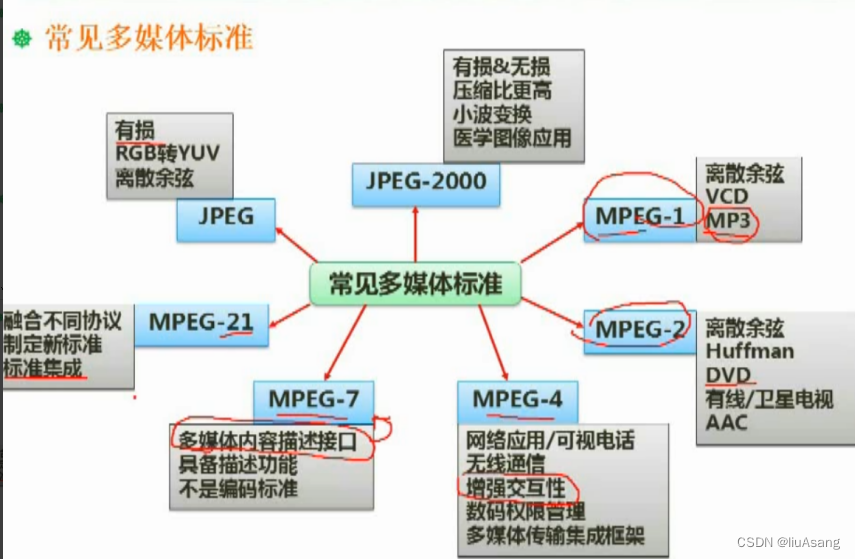
中级软件设计师-note-2

一个逆向思维的例子是 “当遇到一个问题时&#xff0c;通常人们会想办法解决这个问题。但逆向思维是指反过来考虑&#xff0c;即想办法制造更多的问题。 举个例子&#xff0c;假设有一个团队正在开发一款新的智能手机。传统的思维方式可能是专注于如何增加手机的功能&#xf…...

编程日记 2023/12/21 21:25:21

解锁商业宝藏：迅软科技答疑保护商业秘密的重要性

商业秘密指不为公众所知悉、具有商业价值并经权利人采取相应保密措施的技术信息、经营信息等商业信息&#xff0c;一旦泄露可能会给公司带来极大的经济损失和竞争压力&#xff0c;保护商业秘密既能维护企业自身合法权益&#xff0c;也能保障市场经济长期健康发展需求。 保护商…...

编程日记 2023/12/21 21:24:20

【GIT】撤销命令

git add 撤销 add 错误文件&#xff0c;撤销掉add列表的文件使用&#xff1a; git reset [文件名] 撤销单个文件 git reset . 撤销全部 git commit 撤销 commit 之后&#xff0c;但是还没有push 可以用撤回刚刚的commit 记录 git reset HEAD~ git log -v 查看提交记录...

编程日记 2023/12/21 21:22:19

开发知识点-09Rust

Rust Rust 语言通常用于编写系统级软件、网络服务器和高性能应用程序&#xff0c;它具有以下特点&#xff1a;1. 高性能和内存安全&#xff1a;Rust 在保证高性能的同时&#xff0c;利用其所有权模型和借用检查器等特性确保内存安全&#xff0c;避免了 C/C 等语言的内存错误和崩…...

编程日记 2023/12/21 21:21:18

Android开发中，百度语音集成之一

我们在开发中&#xff0c;用到实时语音的时候&#xff0c;会有讯飞、百度、阿里&#xff0c;今天主要讲解的是百度语音之语音合成&#xff1a; public class YuYinUtil { private static final Logger logger LogManager.getLogger(YuYinUtil.class); public static final St…...

编程日记 2023/12/21 21:20:17

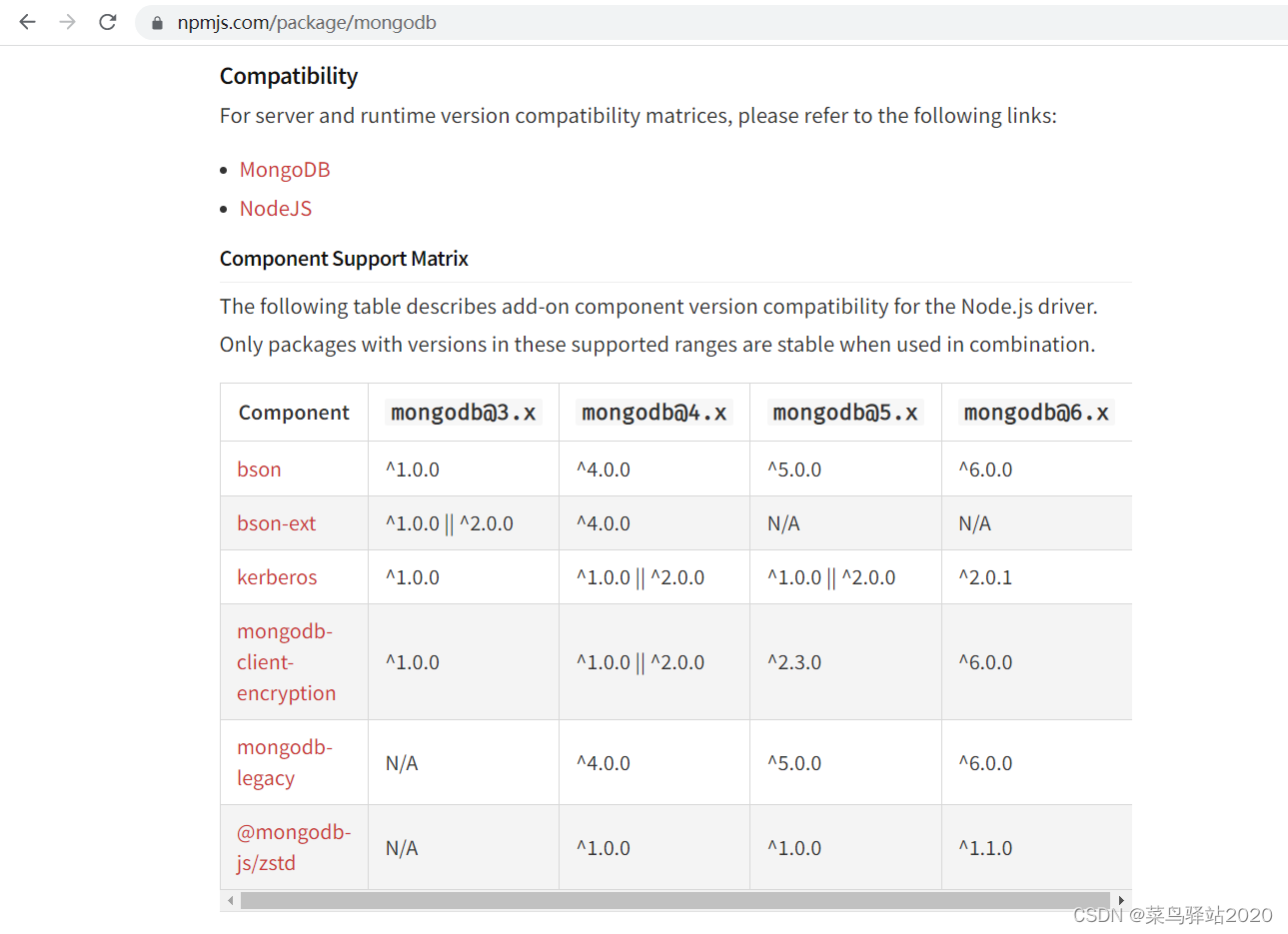
nodejs连接mongodb报错SyntaxError: Unexpected token .

nodejs连接mongodb报错SyntaxError: Unexpected token 如下图 经过排查&#xff0c;原因是npm默认安装的mongodb插件是最新版6.3.0 &#xff0c;而mongodb数据库版本是4.0.0 &#xff0c;两者版本不同导致nodejs报错。 解决方法是npm卸载新版本的mongodb插件&#xff0c;再安…...

编程日记 2023/12/21 21:16:13

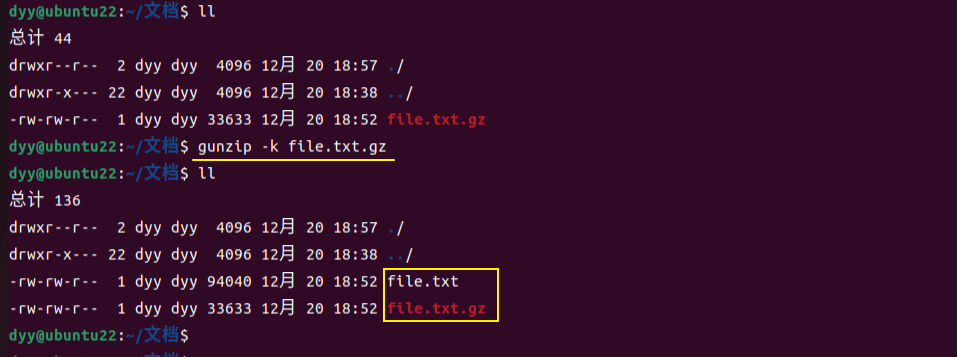
Ubuntu 常用命令之 gunzip 命令用法介绍

&#x1f4d1;Linux/Ubuntu 常用命令归类整理 gunzip是一个在Ubuntu系统下用于解压缩文件的命令。它主要用于解压.gz格式的文件。这个命令是gzip命令的反向操作&#xff0c;gzip用于压缩文件&#xff0c;而gunzip则用于解压缩文件。 gunzip命令的参数有 -c 或 --stdout 或 -…...

编程日记 2023/12/21 21:15:12

sun.misc.BASE64Encoder 进行maven打包时报错

报错如下&#xff1a; 报错代码&#xff0c;是因为引用了sun.misc.BASE64Decoder等类不属于JDK标准库范畴&#xff0c;但在JDK中包含了该类&#xff0c;可以直接使用。在jdk1.9中就不存在了。 import sun.misc.BASE64Decoder; import sun.misc.BASE64Encoder;BASE64Encoder enc…...

编程日记 2023/12/21 21:14:11

[DNS网络] 网页无法打开、显示不全、加载卡顿缓慢 | 解决方案

[网络故障] 网页无法打开、显示不全、加载卡顿缓慢 | 解决方案 问题描述 最近&#xff0c;我在使用CSDN插件浏览 MOOC 网站时&#xff0c;遇到了一些网络故障。具体表现为&#xff1a; MOOC 中国大学慕课网&#xff1a;www.icourse163.org点击CSDN插件首页的 MOOC&#xff08…...

编程日记 2023/12/21 21:13:10

CSS设计器的使用

目录 css的概念 css的优势 css的基本语法 html中引入css样式 CSS基本选择器 选择器的使用 初级选择器&#xff1a; 标签选择器 类选择器 id选择器 高级选择器(结构选择器&#xff09; ①后代选择器(E F) ②子选择器(E>F) ③相邻兄弟选择器(EF) ④通用兄弟选择器(…...

编程日记 2023/12/21 21:11:08

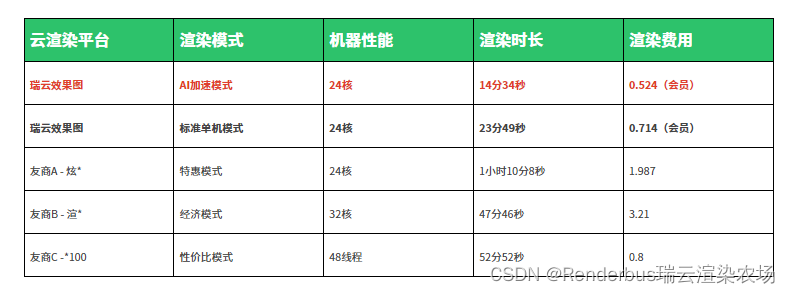
3d渲染太慢怎么办？2024效果图云渲染AI加速来袭

在不断变革的数码技术世界中&#xff0c;三维渲染技术在影视制作、游戏开发以及建筑设计等多个领域得到了广泛运用。然而&#xff0c;高清质量的三维项目的离线渲染时间长久一直是困扰 CG 工作者的一大难题。通常来讲&#xff0c;渲染一帧画面可能需要几分钟到几小时&#xff0…...

编程日记 2023/12/21 21:10:07

指针函数函数指针回调函数相关知识

指针函数&#xff1a; 本质上是一个函数&#xff0c;返回值是一个指针类型&#xff1b;不能返回局部变量的地址&#xff0c;因为其所存储在栈区&#xff0c;在函数调用结束时&#xff0c;被OS回收了&#xff1b;可以返回的情况&#xff1a;全局变量的地址、static修饰的局部变…...

编程日记 2023/12/21 21:09:06

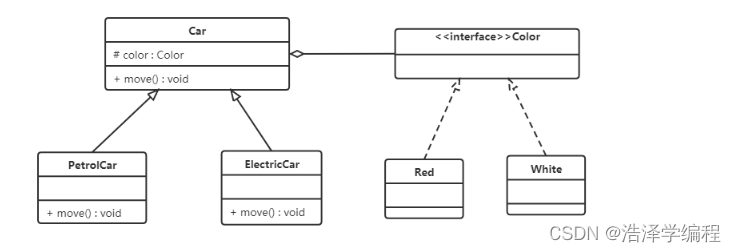
软件设计模式：六大设计原则

文章目录 前言一、开闭原则二、里氏替换原则三、依赖倒转原则四、接口隔离五、迪米特法则六、合成复用原则总结 前言 在软件开发中&#xff0c;为了提高软件系统的可维护性和可复用性&#xff0c;增加软件的可扩展性和灵活性&#xff0c;程序员要尽量根据6条原则来开发程序&am…...

编程日记 2023/12/21 21:07:04

wordpress后台更新后 前端没变化的解决方法

使用siteground主机的wordpress网站&#xff0c;会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后&#xff0c;网站没有变化的情况。 不熟悉siteground主机的新手&#xff0c;遇到这个问题&#xff0c;就很抓狂&#xff0c;明明是哪都没操作错误&#x…...

编程新知 2026/2/9 2:42:46

Vim 调用外部命令学习笔记

Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

编程新知 2025/11/16 8:24:16

vscode里如何用git

打开vs终端执行如下&#xff1a; 1 初始化 Git 仓库&#xff08;如果尚未初始化&#xff09; git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

编程新知 2025/8/24 20:45:38

C++初阶-list的底层

目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

编程新知 2026/2/8 20:42:41

React第五十七节 Router中RouterProvider使用详解及注意事项

前言 在 React Router v6.4 中&#xff0c;RouterProvider 是一个核心组件&#xff0c;用于提供基于数据路由&#xff08;data routers&#xff09;的新型路由方案。 它替代了传统的 <BrowserRouter>&#xff0c;支持更强大的数据加载和操作功能&#xff08;如 loader 和…...

编程新知 2026/2/9 6:48:42

（二）TensorRT-LLM | 模型导出（v0.20.0rc3）

0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述&#xff0c;后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作&#xff0c;其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

编程新知 2026/1/24 6:44:11

镜像里切换为普通用户

如果你登录远程虚拟机默认就是 root 用户&#xff0c;但你不希望用 root 权限运行 ns-3&#xff08;这是对的&#xff0c;ns3 工具会拒绝 root&#xff09;&#xff0c;你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案&#xff1a;创建非 roo…...

编程新知 2025/9/11 11:00:29

【配置 YOLOX 用于按目录分类的图片数据集】

现在的图标点选越来越多&#xff0c;如何一步解决&#xff0c;采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集&#xff08;每个目录代表一个类别&#xff0c;目录下是该类别的所有图片&#xff09;&#xff0c;你需要进行以下配置步骤&#x…...

编程新知 2026/1/30 4:52:56

Maven 概述、安装、配置、仓库、私服详解

目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

编程新知 2026/2/8 1:58:01

Aspose.PDF 限制绕过方案：Java 字节码技术实战分享（仅供学习）

Aspose.PDF 限制绕过方案&#xff1a;Java 字节码技术实战分享&#xff08;仅供学习&#xff09; 一、Aspose.PDF 简介二、说明&#xff08;⚠️仅供学习与研究使用&#xff09;三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

编程新知 2026/2/6 22:13:44