补题与周总结:leetcode第 376 场周赛
文章目录
- 复盘与一周总结
- 2967. 使数组成为等数数组的最小代价(中位数贪心 回文数判断)
- 2968. 执行操作使频率分数最大(中位数贪心 前缀和 滑窗)

复盘与一周总结
wa穿了第3题,赛时其实想到了思路:中位数贪心,从中位数开始,用左右指针找到第一个回文数,与该回文数的代价就是答案。但是没有考虑到左右指针同时找到回文数的情况,wa了一发之后开始改。用一个vector保存代价,只要数组长度大于2就返回其中的较小值。但是没有注意到自己的算法是左右指针同时找,可能出现同一个指针找到两次回文数的情况,此时就不是左右指针分别找到一次回文数。后面改成:数组长度大于5就返回最小值才ac,赛后重写用第一次的思路写了一遍,很快就ac了
现在想想,自己能很快想到正解,但是算法实现的却不是正解,而且赛时还没发现,甚至以为是思路错了,还往平均数那块想了会。只能说,自己在算法实现这块考虑得不仔细吧,下次别着急,想慢点
至于说第4题,赛时完全没有想到中位数贪心,想到哪了呢?我在考虑数组中数的出现次数,出现次数更多的数,最后的代价是否会小于出现次数更小的数。甚至想到:若一个数出现次数超过一半,那么把所有数变为这个数,此时的频率是否最大?接着就对着这个贪心结论证啊证,最后不了了之。但题目的关键点是:操作次数有限,那么就要考虑如何操作能尽可能少的使用操作次数,这样就能想到中位数了
周末这几场打下来,发现自己最大的问题就是:题意的理解。一是读假题,连题目在说什么都没搞清楚,甚至是自以为搞清楚,然后自欺欺人地想算法去了,如abc的E题,小白赛的E题。二是没有抓住题意的重点,只要是稍有难度的题,都需要抓住关键点不断地分析,如这次的第4题,小白赛的F题
问题反而是出现在阅读理解上
2967. 使数组成为等数数组的最小代价(中位数贪心 回文数判断)
2967. 使数组成为等数数组的最小代价 - 力扣(LeetCode)

根据中位数贪心,将数组排序后,从中位数开始,分别向左和向右找到第一个回文数并计算代价,数组两个代价中较小的即可
class Solution {
public:bool f(string s){int l = 0, r = s.size() - 1;while (l < r){if (s[l] != s[r]) return false;l ++ , r -- ;}return true;}long long minimumCost(vector<int>& nums) {sort(nums.begin(), nums.end());int mid;if (nums.size() & 1) mid = nums[nums.size() / 2];else mid = (nums[nums.size() / 2] + nums[nums.size() / 2 - 1]) / 2;long long ans1 = 4e18, ans2 = 4e18;int l = mid, r = mid;while (l >= 0){if (f(to_string(l))){long long t = 0;for (int i = 0; i < nums.size(); ++ i) t += abs(nums[i] - l);ans1 = t;break;}l -- ;}while (r < 2e9){if (f(to_string(r))){long long t = 0;for (int i = 0; i < nums.size(); ++ i) t += abs(nums[i] - r);ans2 = t;break;}r ++ ;}return min(ans1, ans2);}
};
2968. 执行操作使频率分数最大(中位数贪心 前缀和 滑窗)
2968. 执行操作使频率分数最大 - 力扣(LeetCode)

要使将数组中的某些数变成同一个数的代价最小,依然是中位数贪心
同时这个序列必须是原序列的一段连续区间。比如原数组为1,2,3,4,将1,2,3变为2的代价一定比1,2,4变为2的代价小
题目要返回代价小于等于k的情况下,最长的连续区间,对于连续区间问题,自然想到滑动窗口
那么接下来要考虑的是窗口滑动时的代价变化,除了 O ( n ) O(n) O(n)暴力求代价,还能使用前缀和进行预处理, O ( 1 ) O(1) O(1)地求代价
class Solution {
public:int maxFrequencyScore(vector<int>& nums, long long k) {sort(nums.begin(), nums.end());int n = nums.size();vector<long long> a(n + 1), s(n + 1);for (int i = 0; i < n; ++ i) a[i + 1] = nums[i], s[i + 1] = s[i] + a[i + 1];auto f = [&](int l, int mid, int r) -> long long{long long left = (mid - l) * a[mid] - (s[mid - 1] - s[l - 1]);long long right = (s[r] - s[mid - 1]) - (r - mid + 1) * a[mid];return left + right;};int l = 1, r = 1;int ans = 0;while (r <= n){while (f(l, (l + r) / 2, r) > k) l ++ ;ans = max(ans, r - l + 1);r ++ ;}return ans;}
};
相关文章:

补题与周总结:leetcode第 376 场周赛
文章目录 复盘与一周总结2967. 使数组成为等数数组的最小代价(中位数贪心 回文数判断)2968. 执行操作使频率分数最大(中位数贪心 前缀和 滑窗) 复盘与一周总结 wa穿了第3题,赛时其实想到了思路:中位数贪心…...

js指纹库,可跟踪用户唯一性
fingerprintjs官网 资料: Browserleaks - Check your browser for privacy leaks...

Shell三剑客:awk(内部变量)
一、$0 :完整的输入记录 [rootlocalhost ~]# awk -F: {print $0} passwd.txt root:x:0:0:root:/root:/bin/bash bin:x:1:1:bin:/bin:/sbin/nologin daemon:x:2:2:daemon:/sbin:/sbin/nologin adm:x:3:4:adm:/var/adm:/sbin/nologin lp:x:4:7:lp:/var/spool/lpd:/s…...

JVM中的虚拟机栈的动态链接部分存放到底是什么
在Java虚拟机(JVM)中,每个线程在执行一个方法时都会创建一个栈帧(Stack Frame),栈帧中包含了方法的运行时数据。栈帧通常包括局部变量表、操作数栈、动态链接、方法返回地址等部分。 动态链接 动态链接&a…...
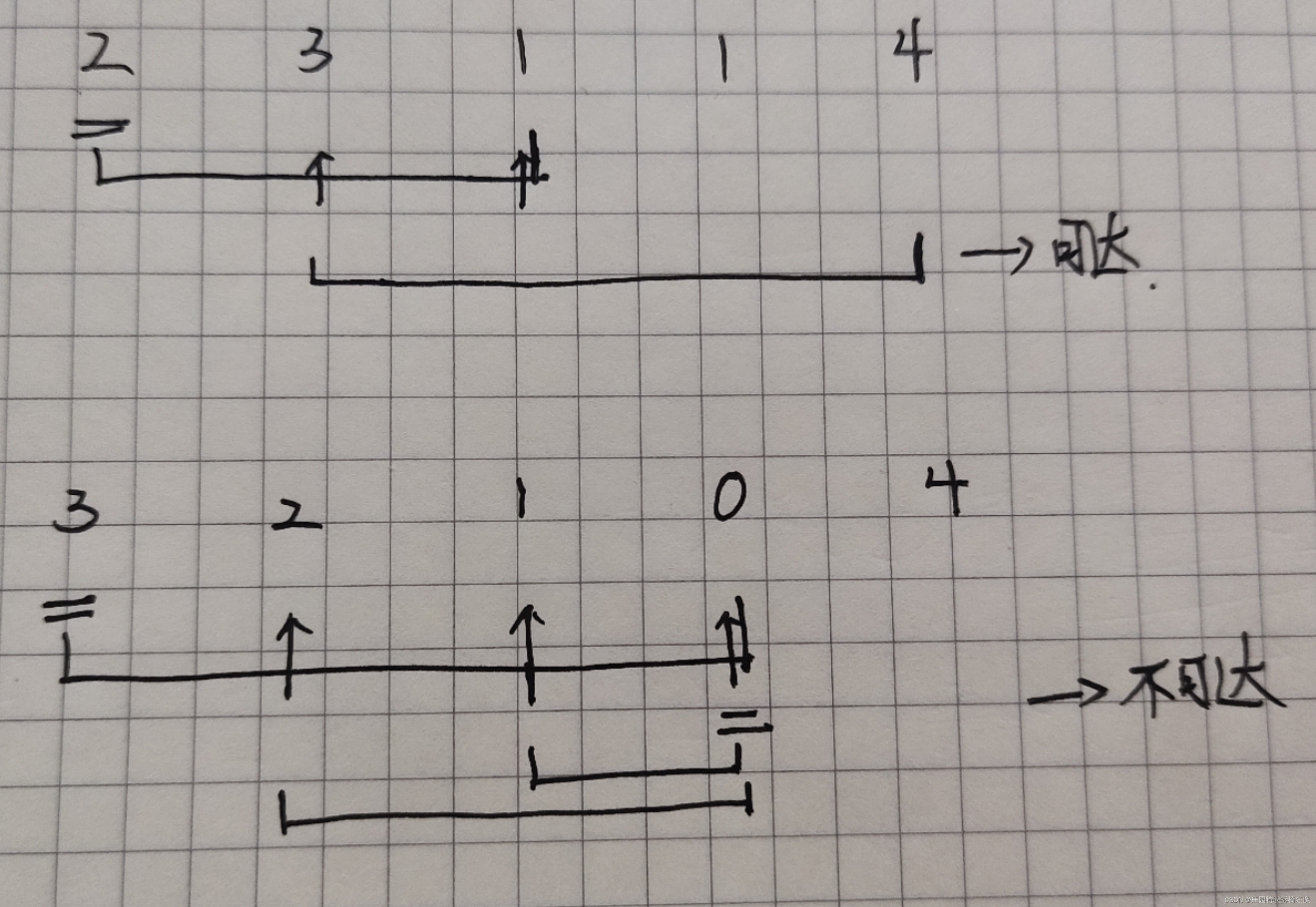
Leetcode 55 跳跃游戏
题意理解: 非负整数数组 nums, 最初位于数组的 第一个下标 。 数组中的每个元素代表你在该位置可以跳跃的最大长度。 需要跳到nums最后一个元素即为成功。 目标:是否能够跳到最后一个元素。 解题思路: 使用贪心算法来解题,需要理解…...

构建陪诊预约系统:技术实战指南
在医疗科技的飞速发展中,陪诊预约系统的应用为患者和陪诊人员提供了更为便捷和贴心的服务。本文将带领您通过技术实现,构建一个简单而实用的陪诊预约系统,以提升医疗服务的效率和用户体验。 技术栈选择 在开始之前,我们需要选择…...

windows和linux将文件删除至回收站【C++】【Go】语言实现
目录 C Windows平台 Linux平台 开平台,代码合并 Go 实现步骤 Go语言实现示例 go单独的windows版本实现 代码解释 C 在C中,将文件移动到回收站的实现在Linux和Windows平台上是不同的。首先,我会为你提供在Windows平台上实现的代码示例…...

10 Vue3中v-html指令的用法
概述 v-html主要是用来渲染富文本内容,比如评论信息,新闻信息,文章信息等。 v-html是一个特别不安全的指令,因为它会将文本以HTML的显示进行渲染,一旦文本里面包含一些恶意的js代码,可能会导致整个网页发…...
华为数通方向HCIP-DataCom H12-831题库(多选题:181-200)
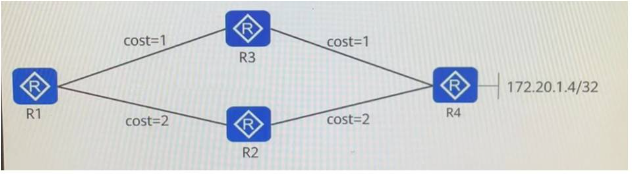
第181题 如图所示,R1、R2、R3、R4都部署为SPF区域0,链路的cost值如图中标识。R1、R2R3、R4的Loopback0通告入OSPF。R1、R2、R3与R4使用Loopback0作为连接接口,建立BGP对等体关系,其中R4为RR设备,R1、R2、R3是R4的客户端。当R4的直连地址172.20,1,4/32通告入BGP后,以下关R…...
DC-磁盘管理
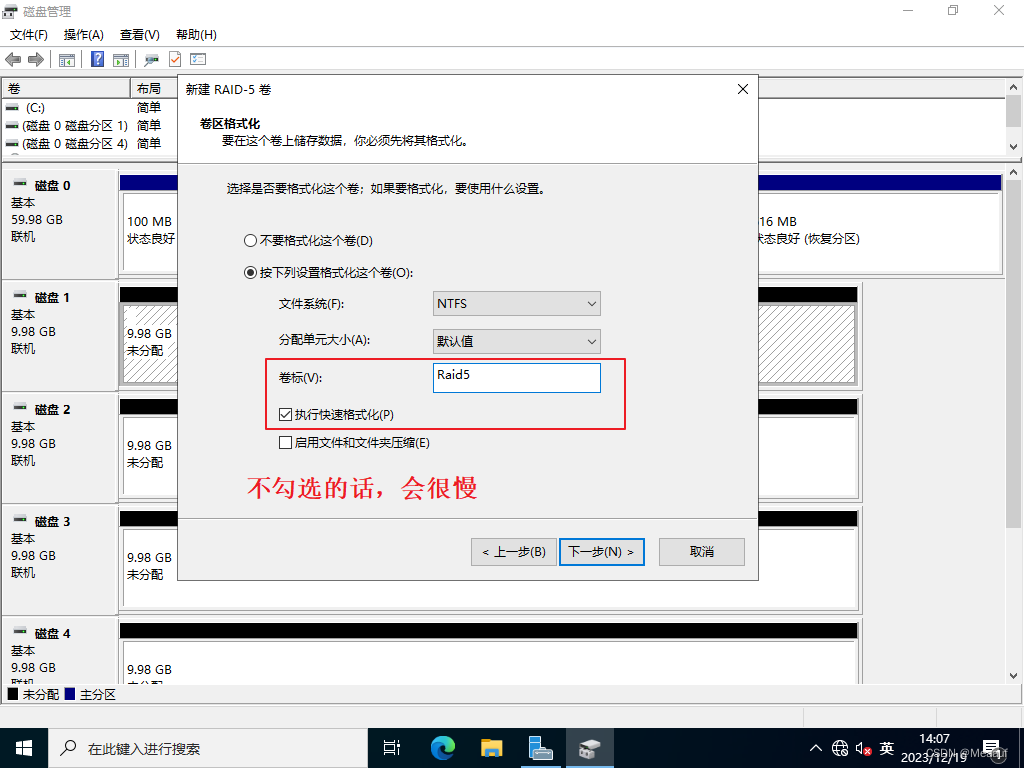
2023年全国网络系统管理赛项真题 模块B-Windows解析 题目 在DC2上安装及配置软RAID 5。在安装好的DC2虚拟机中添加三块10G虚拟磁盘。组成RAID 5,磁盘分区命名为卷标H盘:Raid5。手动测试破坏一块磁盘,做RAID磁盘修复,确认RAID 5配置完毕。配置步骤 关闭虚拟机,添加3块10G磁…...

使用Docker运行镜像文件与设置端口
1,创建镜像文件前准备 # 使用基础镜像FROM alpine:latest# 设置工作目录WORKDIR /app# 复制应用程序文件到镜像中COPY . .# 暴露容器的端口 不会自动将容器的端口映射到宿主机上 docker run -d -p <宿主机端口>:7080 <镜像名称>EXPOSE 7080# 定义容器启…...

Centos 8.5 Oracle12c安装
由于多次安装踩坑,所以本次写了一份12c安装的完整版。可以直接使用。 一、安装数据库基本信息 名称 值 主机名 database 操作系统 CentOS Linux release 8.5.2111 Oracle用户名/密码 oracle Oracle 版本 12c Enterprise Edition Release 12.2.0.1.0 oracle…...
Apache Tomcat httpoxy 安全漏洞 CVE-2016-5388 已亲自复现
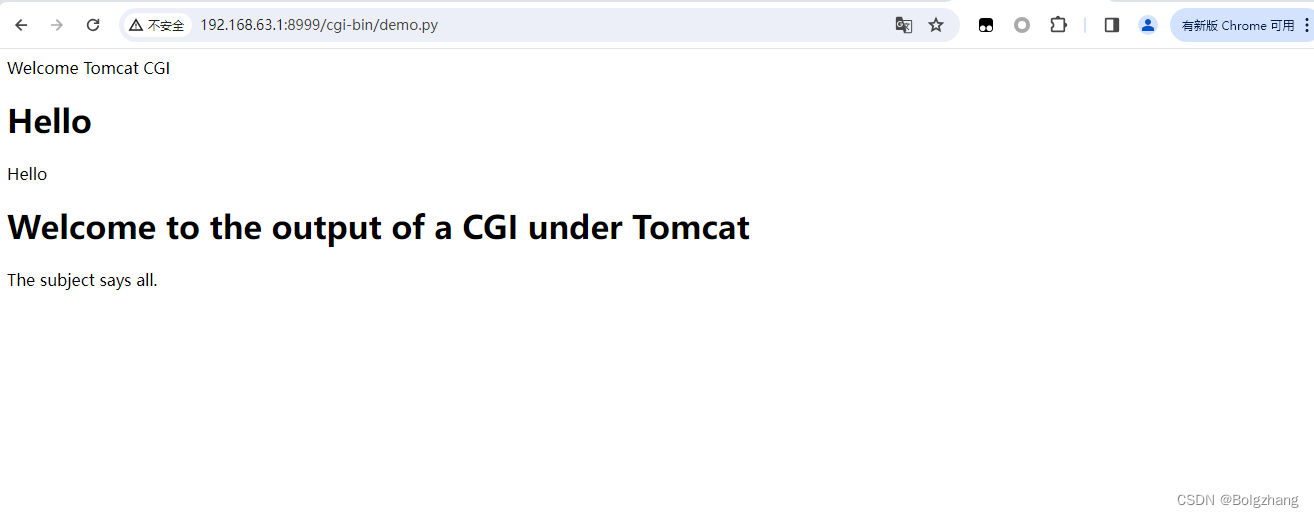
Apache Tomcat httpoxy 安全漏洞 CVE-2016-5388 已亲自复现 漏洞名称漏洞描述影响版本 漏洞复现环境搭建漏洞利用 修复建议总结 漏洞名称 漏洞描述 在Apache Tomcat中发现了一个被归类为关键的漏洞,该漏洞在8.5.4(Application Server Soft ware)以下。受影响的是组…...

ChatGLM3-6B 的调用参数说明,chat 与stream_chat 接口函数的参数说明
ChatGLM3-6B 是一个语言大模型,最近在评估这个模型,但发现它的文档有限,只能从demo代码中猜测调用的参数的含义,准确度是有限的;于是,通过查看源代码来研究,目前整理笔记如下: Chat…...
Vuex的学习-2
Vuex的核心概念 StateMutationAction 1.State State提供唯一的公共数据源,所有共享的数据都统一放在Store的State中进行存储。 const store new Vuex.Store({state : { count: 0 } }) 这是渲染的页面 组件访问数据的第一种方式 组件访问数据的第二种方式 // 1…...
智慧安防视频监控EasyCVR如何通过回调接口向第三方平台推送RTSP视频通道离线通知
安防视频监控系统EasyCVR能在局域网、公网、专网等复杂的网络环境中部署,可支持4G、5G、WiFi、有线等方式进行视频的接入与传输、处理和分发。平台能将接入的视频流进行汇聚、转码、多格式输出和分发,具体包括:RTMP、RTSP、HTTP-FLV、WebSock…...

Scrum项目管理流程及免费敏捷工具
项目启动: 团队明确项目愿景、目标和范围,确定项目范围和优先级,并建立团队以及开展初步计划。 制定产品待办事项清单(Product Backlog): 定义项目所需功能、任务和需求列表,并按优先级排序…...

大型医院PACS系统源码,影像存储与传输系统源码,支持多种图像处理及三维重建功能
PACS系统是医院影像科室中应用的一种系统,主要用于获取、传输、存档和处理医学影像。它通过各种接口,如模拟、DICOM和网络,以数字化的方式将各种医学影像,如核磁共振、CT扫描、超声波等保存起来,并在需要时能够快速调取…...
HDFS NFS Gateway(环境配置,超级详细!!)
HDFS NFS Gateway简介: HDFS NFS Gateway是Hadoop Distributed File System(HDFS)中的一个组件,它允许客户端通过NFS(Network File System,网络文件系统)与HDFS进行交互。具体来说,HDFS NFS…...

nginx 离线安装 https反向代理
这里写自定义目录标题 安装步骤1.安装nginx所需依赖1.1 安装gcc和gcc-c1.1.1下载依赖包1.1.2 上传依赖包1.1.3安装依赖 1.2 安装pcre1.2.1 下载pcre1.2.2 上传解压安装包1.2.3 编译安装 1.3 下载安装zlib1.3.1 下载zlib1.3.2 上传解压安装包1.3.3 编译安装 1.4 下载安装openssl…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
