【每日一题】得到山形数组的最少删除次数
文章目录
- Tag
- 题目来源
- 解题思路
- 方法一:最长递增子序列
- 写在最后
Tag
【最长递增子序列】【数组】【2023-12-22】
题目来源
1671. 得到山形数组的最少删除次数

解题思路
方法一:最长递增子序列
前后缀分解
根据前后缀思想,以 nums[i] 为山顶的山形数组可以看成 nums[i] 左侧以其作为结尾的最长递增子序列,我们记左侧的最长递增子序列的长度为 pre[i],拼接上 nums[i] 右侧以其作为结尾的最长递减子序列,我们记右侧的最长递减子序列的长度为 suf[i],此时以 nums[i] 为山顶的山形数组长度为:
p r e [ i ] + s u f [ i ] − 1 pre[i] + suf[i] - 1 pre[i]+suf[i]−1
我们枚举所有的 nums[i],计算所有的最长山顶数组长度 maxLen,最后需要删除的数组元素长度为 n - maxLen 即为最后需要返回的答案。
最长递增子序列
如何计算 pre 和 suf ?
pre 和 suf 的计算过程类似。先来看一下 pre 的计算。维护数组 pre,pre[i] 表示以 nums[i] 作为结尾的最长递增子序列的长度;维护辅助数组 g,表示以当前元素 nums[i] 结尾的最长递增子序列数组。
遍历数组 nums,当前遍历的元素为 nums[i] 记为 x,在数组 g 中使用二分查找找到第一个大于 x 的元素,对应的位置为 it - g.begin() + 1:
- 更新
pre[i] = it - g.begin() + 1; - 如果 x 不在 g 中,则将 x 加入 g;否则将 x 更新到 g 中相应的位置。
在 suf 的计算过程中,我们从后往前遍历数组 nums,就是找最长的递增子序列,于是计算过程和 pre 的计算类似。
remark1:因为山峰不可能在数组首和尾两个位置出现,那么在遍历所有山峰的范围
[0, n-1]时,需要先做判断pre[i] >= 2 && suf[i] >= 2。
remark2:可以先计算
suf,然后一起计算pre和更新答案的,留给读者自己实现。
算法
class Solution {
public:int minimumMountainRemovals(vector<int>& nums) {int n = nums.size();vector<int> pre(n), g;for (int i = 0; i < n; ++i) {int x = nums[i];auto it = lower_bound(g.begin(), g.end(), x);pre[i] = it - g.begin() + 1;if (it == g.end()) {g.push_back(x);}else {*it = x;}}vector<int> suf(n);g.clear();for (int i = n - 1; i >= 0; --i) {int x = nums[i];auto it = lower_bound(g.begin(), g.end(), x);suf[i] = it - g.begin() + 1;if (it == g.end()) {g.push_back(x);}else {*it = x;}}int mx = 0;for (int i = 1; i < n - 1; ++i) {mx = max(mx, pre[i] + suf[i] - 1);}return n - mx;}
};
复杂度分析
时间复杂度: O ( n l o g n ) O(nlogn) O(nlogn),更新 pre 和 suf 的时间复杂度都为 O(nlogn),更新答案的时间复杂度为 O ( n ) O(n) O(n)。
空间复杂度: O ( n ) O(n) O(n),额外占用的空间为数组 pre、suf 和 g。空间复杂度: O ( n ) O(n) O(n),额外占用的空间为数组 pre、suf 和 g。
写在最后
如果您发现文章有任何错误或者对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度的方法,欢迎评论区交流。
最后,感谢您的阅读,如果有所收获的话可以给我点一个 👍 哦。
相关文章:

【每日一题】得到山形数组的最少删除次数
文章目录 Tag题目来源解题思路方法一:最长递增子序列 写在最后 Tag 【最长递增子序列】【数组】【2023-12-22】 题目来源 1671. 得到山形数组的最少删除次数 解题思路 方法一:最长递增子序列 前后缀分解 根据前后缀思想,以 nums[i] 为山…...

2023年,为什么汽车依然有很多小毛病?
汽车出现小毛病是一个复杂的问题,其原因涉及到汽车本身的设计、制造质量、维护保养以及使用环境等多个方面。只有汽车制造商、车主和社会各界共同努力,才能够减少汽车的小毛病,提高汽车的可靠性和安全性。 比如,汽车的维护和保养…...

yocto系列讲解[实战篇]93 - 添加Qtwebengine和Browser实例
By: fulinux E-mail: fulinux@sina.com Blog: https://blog.csdn.net/fulinus 喜欢的盆友欢迎点赞和订阅! 你的喜欢就是我写作的动力! 目录 概述集成meta-qt5移植过程中的问题问题1:virtual/libgl set to mesa, not mesa-gl问题2:dmabuf-server-buffer tries to use undecl…...
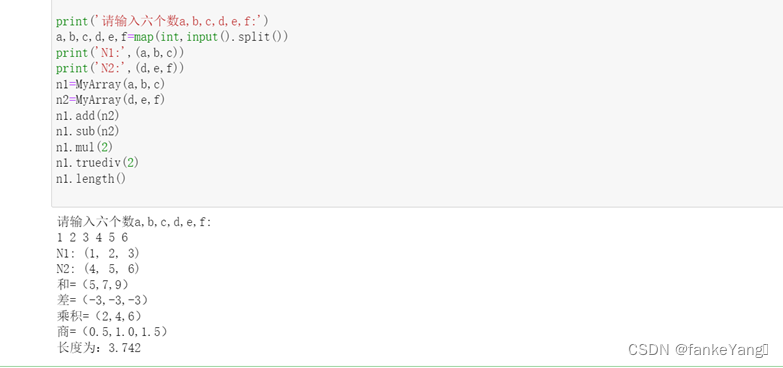
Python实验报告十一、自定义类模拟三维向量及其运算
一、实验目的: 1、了解如何定义一个类。 2、了解如何定义类的私有数据成员和成员方法。 3、了解如何使用自定义类实例化对象。 二、实验内容: 定义一个三维向量类,并定义相应的特殊方法实现两个该类对象之间的加、减运算(要…...
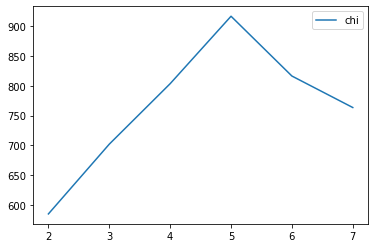
机器学习 | 聚类Clustering 算法
物以类聚人以群分。 什么是聚类呢? 1、核心思想和原理 聚类的目的 同簇高相似度 不同簇高相异度 同类尽量相聚 不同类尽量分离 聚类和分类的区别 分类 classification 监督学习 训练获得分类器 预测未知数据 聚类 clustering 无监督学习,不关心类别标签 …...
IntelliJ IDEA 2023.3 新功能介绍
IntelliJ IDEA 2023.3 在众多领域进行了全面的改进,引入了许多令人期待的功能和增强体验。以下是该版本的一些关键亮点: IntelliJ IDEA mac版下载 macappbox.com/a/intellij-idea-for-mac.html 1. AI Assistant 的全面推出 IntelliJ IDEA 2023.3 中&am…...
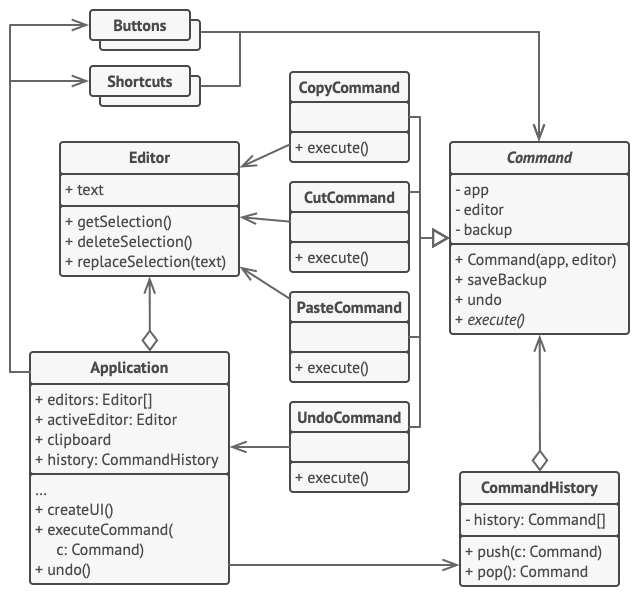
2. 行为模式 - 命令模式
亦称: 动作、事务、Action、Transaction、Command 意图 命令模式是一种行为设计模式, 它可将请求转换为一个包含与请求相关的所有信息的独立对象。 该转换让你能根据不同的请求将方法参数化、 延迟请求执行或将其放入队列中, 且能实现可撤销…...
Java智慧工地源码 SAAS智慧工地源码 智慧工地管理可视化平台源码 带移动APP
一、系统主要功能介绍 系统功能介绍: 【项目人员管理】 1. 项目管理:项目名称、施工单位名称、项目地址、项目地址、总造价、总面积、施工准可证、开工日期、计划竣工日期、项目状态等。 2. 人员信息管理:支持身份证及人脸信息采集&#…...

php学习02-php标记风格
<?php echo "这是xml格式风格" ?><script language"php">echo 脚本风格标记 </script><% echo "这是asp格式风格" %>推荐使用xml格式风格 如果要使用简短风格和ASP风格,需要在php.ini中对其进行配置&#…...

13.1 jar文件
13.1 jar文件 java归档(JAR)文件,将应用程序打包后仅提供的单独文件,可包含类文件,也可包含图片、声音等其他类型文件。 JAR文件使用了大家熟悉的Zip压缩格式,pack200为通常的zip压缩算法,对类…...

论文阅读:Long-Term Visual Simultaneous Localization and Mapping
论文摘要指出,为了在长期变化的环境中准确进行定位,提出了一种新型的长期视觉SLAM(同步定位与地图构建)系统,该系统具备地图预测和动态物体移除功能。系统首先设计了一个高效的视觉点云匹配算法,将2D像素信…...
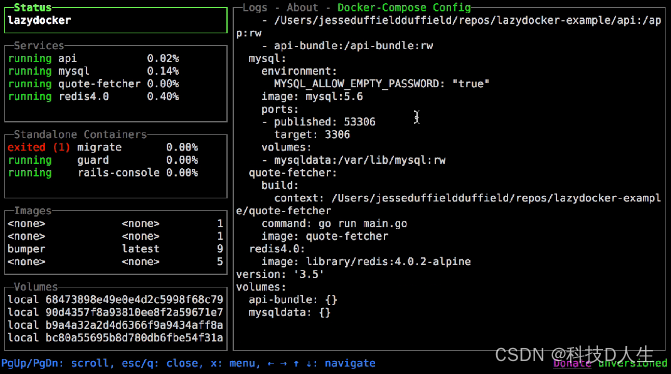
Docker 学习总结(80)—— 轻松驾驭容器,玩转 LazyDocker
前言 LazyDocker 是一个用户友好的命令行工具,简化了 Docker 的管理。它能够通过单一命令执行常见的 Docker 任务,如启动、停止、重启和移除容器。LazyDocker 还能轻松查看日志、清理未使用的容器和镜像,并自定义指标。 简绍 LazyDocker 是一个用户友好的 CLI 工具,可以轻…...
- MediaCodecList)
Android 13 - Media框架(24)- MediaCodecList
这一节我们要了解 MediaCodecList 中的信息是如何加载的,以及这些信息是如何使用到的。 // static sp<IMediaCodecList> MediaCodecList::getLocalInstance() {Mutex::Autolock autoLock(sInitMutex);if (sCodecList nullptr) {MediaCodecList *codecList n…...

【稳定检索|投稿优惠】2024年交通运输与能源动力国际学术会议(IACTEP 2024)
2024年交通运输与能源动力国际学术会议(IACTEP 2024) 2024 International Academic Conference on Transportation and Energy Power(IACTEP) 一、【会议简介】 2024年交通运输与能源动力国际学术会议(IACTEP 2024)将在美丽的三亚盛大启幕。本次会议将聚焦交通运输与能源动力等…...
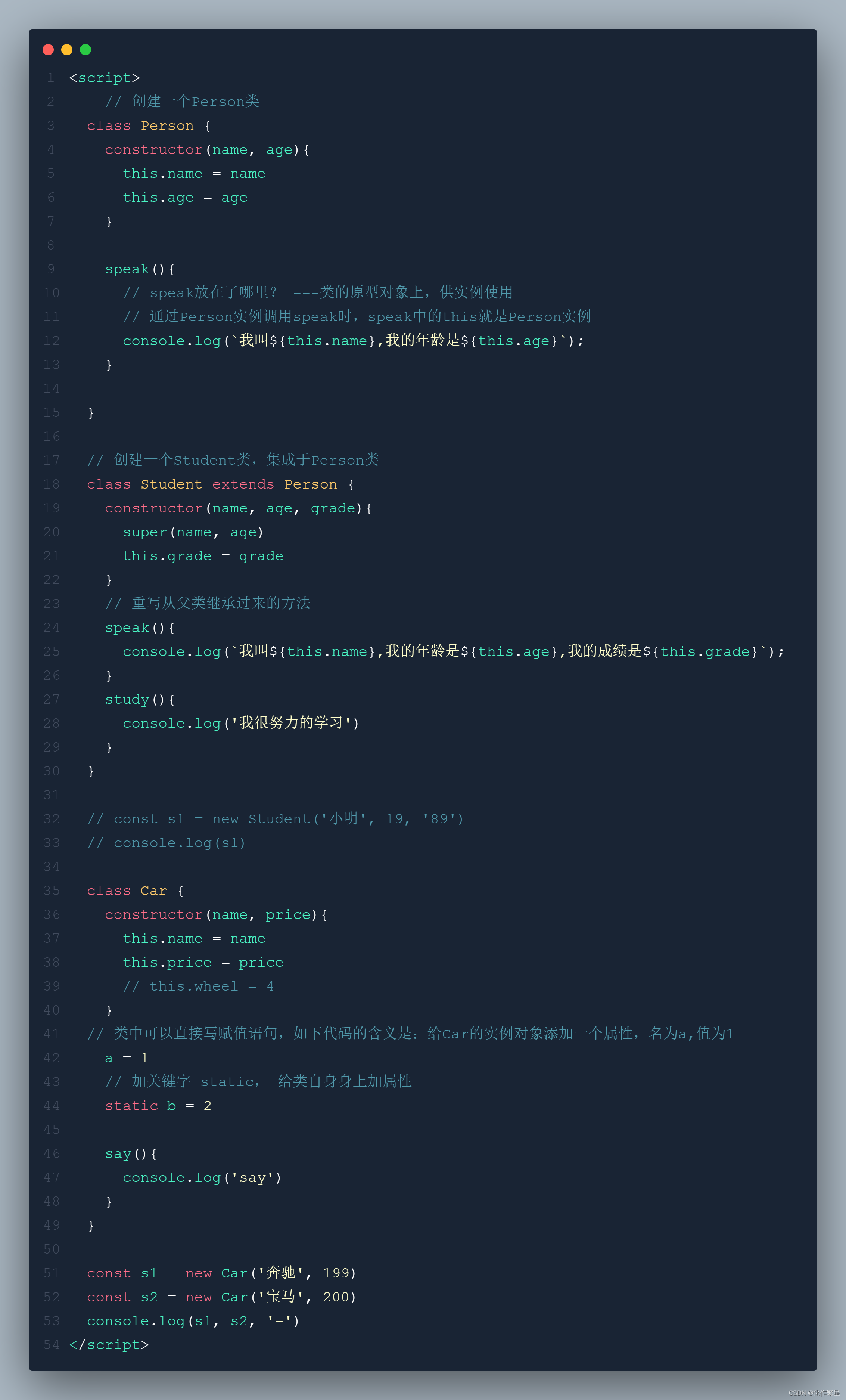
React学习计划-React16--React基础(三)收集表单数据、高阶函数柯里化、类的复习
1. 收集表单数据 包含表单的组件分类 受控组件——页面中所有输入类的DOM,随着输入,把值存维护在状态里,需要用的时候去状态里取值(推荐,避免了过渡使用ref)非受控组件——页面中所有输入类的DOM,现用现取…...

研究生课程 |《数值分析》复习
搭配往年真题册食用最佳。...

55 回溯算法解黄金矿工问题
问题描述:你要开发一座金矿,地质学家已经探明了这座金矿中的资源分布,并用大小为m*n的网格grid进行了标注,每个单元格中的整数就表示这一单元格中的黄金数量;如果单元格是空的,那么就是0,为了使…...
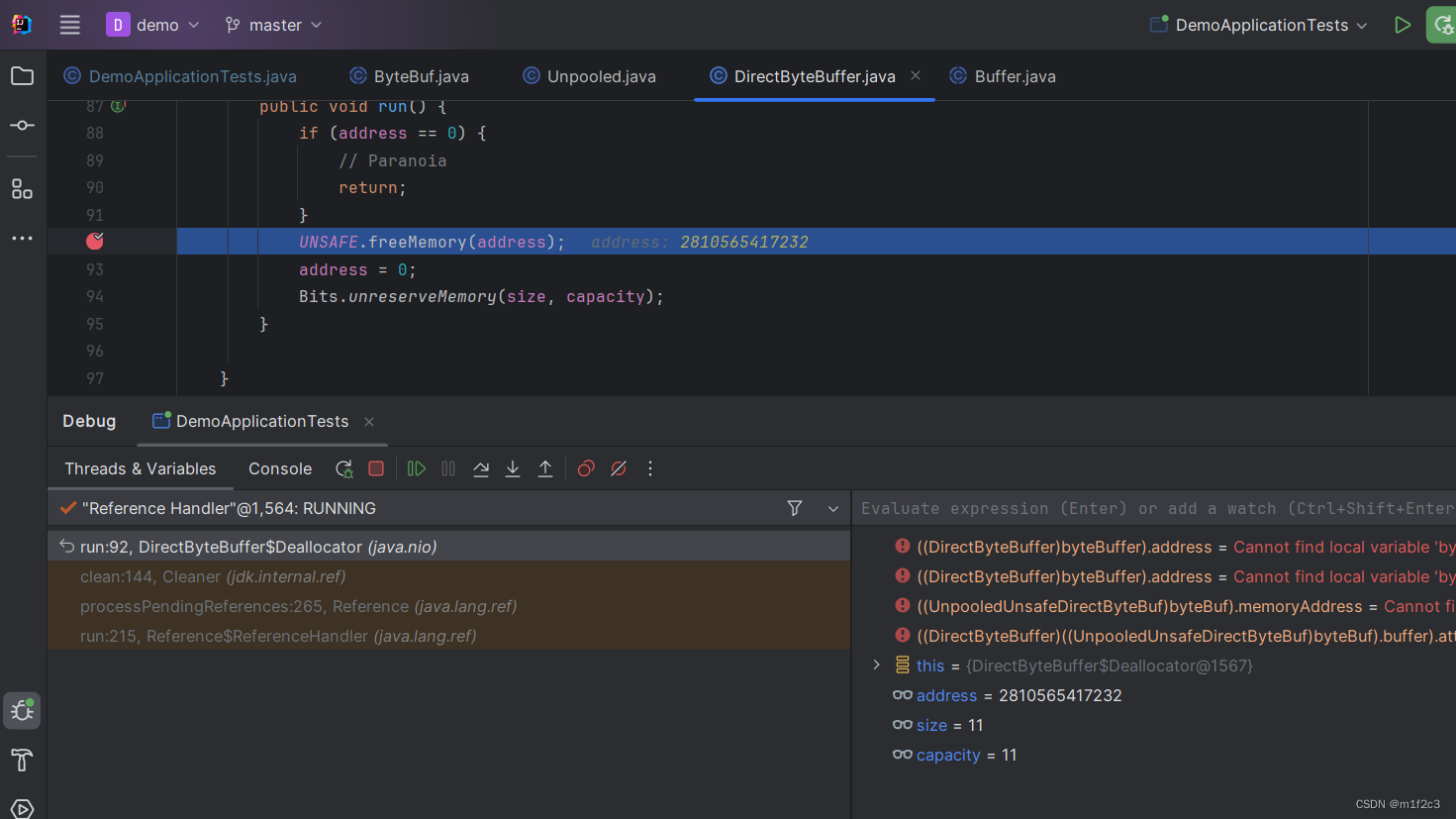
[笔记]ByteBuffer垃圾回收
参考:https://blog.csdn.net/lom9357bye/article/details/133702169 public static void main(String[] args) throws Throwable {List<Object> list new ArrayList<>();Thread thread new Thread(() -> {ByteBuffer byteBuffer ByteBuffer.alloc…...

c++ opencv中unsigned char *、Mat、Qimage互相转换
unsigned char * 转Mat unsinged char * data img.data; Mat mat (h,w,cv_8UC3,data,0);void * 转Qimage uchar * bit (uchar*)pRknnInputData; QImage image QImage(bit, 2048,1536, QImage::Format_RGB888);qimage转Mat QImage image QImage (MODEL_INPUT_WIDTH_SIZE,MODE…...
法线贴图实现衣服上皱褶特效
在线工具推荐: 3D数字孪生场景编辑器 - GLTF/GLB材质纹理编辑器 - 3D模型在线转换 - Three.js AI自动纹理开发包 - YOLO 虚幻合成数据生成器 - 三维模型预览图生成器 - 3D模型语义搜索引擎 法线贴图在3D建模中扮演着重要的角色,它通过模拟表面的微…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...

如何通过git命令查看项目连接的仓库地址?
要通过 Git 命令查看项目连接的仓库地址,您可以使用以下几种方法: 1. 查看所有远程仓库地址 使用 git remote -v 命令,它会显示项目中配置的所有远程仓库及其对应的 URL: git remote -v输出示例: origin https://…...

MLP实战二:MLP 实现图像数字多分类
任务 实战(二):MLP 实现图像多分类 基于 mnist 数据集,建立 mlp 模型,实现 0-9 数字的十分类 task: 1、实现 mnist 数据载入,可视化图形数字; 2、完成数据预处理:图像数据维度转换与…...
