【算法设计与分析】——动态规划算法
🎃个人专栏:
🐬 算法设计与分析:算法设计与分析_IT闫的博客-CSDN博客
🐳Java基础:Java基础_IT闫的博客-CSDN博客
🐋c语言:c语言_IT闫的博客-CSDN博客
🐟MySQL:数据结构_IT闫的博客-CSDN博客
🐠数据结构:数据结构_IT闫的博客-CSDN博客
💎C++:C++_IT闫的博客-CSDN博客
🥽C51单片机:C51单片机(STC89C516)_IT闫的博客-CSDN博客
💻基于HTML5的网页设计及应用:基于HTML5的网页设计及应用_IT闫的博客-CSDN博客
🥏python:python_IT闫的博客-CSDN博客
🐠离散数学:离散数学_IT闫的博客-CSDN博客
欢迎收看,希望对大家有用!
目录
🎯内容概括:
🎯目的:
🎯基本步骤:
🎯环境:
🎯内容:
💻one:
🎃问题:
🎃解题思路:
🎃代码分析:
🎃总代码:
🎃 运行截图:
💻two:
🎃问题:
🎃解题思路:
🎃代码分析:
🎃总代码:
🎃运行截图:
💻three:
🎃问题:
🎃解题思路:
🎃代码分析:
🎃总代码:
🎯 做题方法总结:
🎯内容概括:
1)矩阵连乘问题:已知矩阵A1A2A3A4A5 ,使用向量P<P0=3,P1=2,P2=5,P3=10,P4=2,P5=3>存储行列,求出相乘次数最少的加括号位置。
2)0-1背包问题:有5个物品,其重量分别为{2,2,6,5,4},价值分别为{6,3,5,4,6}。背包容量为10,物品不可分割,求装入背包的物品和获得的最大价值。
3)最长公共子序列问题:求X={A,B,C,B,D,A,B}和Y={B,D,C,A,B,A}的最长公共子序列。
🎯目的:
1)了解动态规划算法思想;
2)掌握算法的基本要素及解题步骤;
3)能够对实际问题,能够按照动态规划解题步骤,分析问题;
4)能够正确的编码、实现动态规划算法;
5)能够正确分析算法的时间复杂度和空间复杂度。
🎯基本步骤:
1)审阅题目,明确题目的已知条件和求解的目标;
2)问题建模;
3)算法设计;
4)编码实现(语言不限);
5)测试数据;
6)程序运行结果;
7)分析实验结果是否符合预期,如果不符合,分析可能的原因;
8)算法分析。
🎯环境:
VC6.0 / Eclipse / Pycharm。
🎯内容:
💻one:
🎃问题:
1)矩阵连乘问题:已知矩阵A1A2A3A4A5 ,使用向量P<P0=3,P1=2,P2=5,P3=10,P4=2,P5=3>存储行列,求出相乘次数最少的加括号位置。
🎃解题思路:
- 创建两个二维数组m和s,其中m[i][j]表示从矩阵Ai到Aj的连乘所需的最少次数,s[i][j]表示从矩阵Ai到Aj的连乘的最优加括号位置。
- 初始化m[i][i]为0,表示单个矩阵相乘的次数为0。
- 对于长度l=2到n的子链长度,依次计算m[i][j]和s[i][j]
- 遍历每个可能的分割点k,计算m[i][j]的值。
- m[i][j]的值等于m[i][k] + m[k+1][j] + Pi-1 * Pk * Pj。
- 更新m[i][j]时,同时更新s[i][j]为k,表示在Ai到Aj之间最优的加括号位置是在矩阵Ak与Ak+1之间。
4.最终,m[1][n]存储的即为从A1到An连乘的最小次数。
🎃代码分析:
matrix1方法:
public static void matrix1(int[] p) {int n = p.length - 1;int[][] x = new int[n][n];int[][] y = new int[n][n];for (int l = 2; l <= n; l++) {for (int i = 0; i < n - l + 1; i++) {int j = i + l - 1;x[i][j] = Integer.MAX_VALUE;for (int k = i; k < j; k++) {int q = x[i][k] + x[k + 1][j] + p[i] * p[k + 1] * p[j + 1];if (q < x[i][j]) {x[i][j] = q;y[i][j] = k;}}}}System.out.println("相乘次数最少的加括号的位置为:");print(y, 0, n - 1);System.out.println();System.out.println("最少相乘次数:" + x[0][n - 1]);
}这个方法使用动态规划来解决矩阵链乘问题。它通过填充二维数组
x和y来计算最少相乘次数和最优加括号位置。
public static void print(int[][] s, int i, int j) {if (i == j) {System.out.print("A" + (i + 1));} else {System.out.print("(");print(s, i, s[i][j]);print(s, s[i][j] + 1, j);System.out.print(")");}
}这个方法用于打印最优加括号位置。根据数组
s中存储的最优加括号位置信息,递归地打印出最优的加括号位置。
main方法:
public static void main(String[] args) {int[] m = { 3, 2, 5, 10, 2, 3 };matrix1(m);
}这是程序的入口,在这里创建了一个整型数组
m,表示矩阵的维度。然后调用matrix1方法来解决矩阵连乘问题。
🎃总代码:
package test20210110;public class Test01 {public static void matrix1(int[] p) {int n = p.length - 1;int[][] x = new int[n][n];int[][] y = new int[n][n];for (int l = 2; l <= n; l++) {for (int i = 0; i < n - l + 1; i++) {int j = i + l - 1;x[i][j] = Integer.MAX_VALUE;for (int k = i; k < j; k++) {int q = x[i][k] + x[k + 1][j] + p[i] * p[k + 1] * p[j + 1];if (q < x[i][j]) {x[i][j] = q;y[i][j] = k;}}}}System.out.println("相乘次数最少的加括号的位置为:");print(y, 0, n - 1);System.out.println();System.out.println("最少相乘次数:" + x[0][n - 1]);}public static void print(int[][] s, int i, int j) {if (i == j) {System.out.print("A" +(i+1));} else {System.out.print("(");print(s, i, s[i][j]);print(s, s[i][j] + 1, j);System.out.print(")");}}public static void main(String[] args) {int[] m = { 3, 2, 5, 10, 2, 3 };matrix1(m);}
}🎃 运行截图:
💻two:
🎃问题:
2)0-1背包问题:有5个物品,其重量分别为{2,2,6,5,4},价值分别为{6,3,5,4,6}。背包容量为10,物品不可分割,求装入背包的物品和获得的最大价值。
🎃解题思路:
首先,定义一个二维数组
dp,其中dp[i][j]表示在前i个物品中,背包容量为j时能够获得的最大价值。然后,初始化边界条件。当没有物品可选或者背包容量为0时,最大价值都为0。因此,可以将
dp[0][j]和dp[i][0](其中0 ≤ i ≤ 5,0 ≤ j ≤ 10)都设置为0。接下来,通过两层循环遍历物品和背包容量。外层循环表示当前所选物品的数量,从1到5;内层循环表示背包容量,从1到10。
在每次迭代中,分为两种情况进行考虑:
- 若当前物品重量大于当前背包容量,则无法选择该物品,因此
dp[i][j]的值与dp[i-1][j]相等。- 若当前物品重量小于等于当前背包容量,则需要进行选择。可以比较将该物品放入背包后的总价值与不放入该物品的总价值,选择其中较大的一个。即
dp[i][j]的值为max(dp[i-1][j], dp[i-1][j-w[i]]+v[i]),其中w[i]表示第i个物品的重量,v[i]表示第i个物品的价值。完成所有的循环后,
dp[5][10]中存储的即为装入背包的物品能够获得的最大价值。
🎃代码分析:
首先,定义了一个
Value类,并在main方法中编写了解决0-1背包问题的代码。
int[] weight = { 2, 2, 6, 5, 4 };
int[] value = { 6, 3, 5, 4, 6 };
int a = 10;int[][] dp = new int[weight.length + 1][a + 1];
以上代码定义了物品的重量数组
weight、价值数组value和背包容量a。同时,创建了一个二维数组dp,大小为(weight.length + 1) × (a + 1),用于存储状态转移的结果。
for (int i = 1; i <= weight.length; i++) {for (int j = 1; j <= a; j++) {if (j >= weight[i - 1]) {dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + value[i - 1]);} else {dp[i][j] = dp[i - 1][j];}}
}以上代码通过两层循环遍历物品和背包容量,实现了动态规划的过程。在每次迭代中,根据当前物品重量和背包容量的大小关系,选择将该物品放入背包还是不放入背包,并更新
dp数组中相应位置的值。具体而言,如果当前物品的重量小于等于背包容量,则需要考虑将该物品放入背包后是否能够获得更大的总价值。通过比较不放入该物品和放入该物品两种情况下的总价值,选择其中较大的一个,并更新
dp[i][j]的值。如果当前物品的重量大于背包容量,则无法放入该物品,直接将
dp[i][j]的值设为上一个状态dp[i-1][j]的值。
System.out.print("装入的物品是第");
int i = weight.length;
int j = a;
while (i > 0 && j > 0) {if (dp[i][j] != dp[i - 1][j]) {System.out.print(i + "个,");j -= weight[i - 1];}i--;
}System.out.println("\n最大价值为:" + dp[weight.length][a]);
以上代码用于输出装入背包的物品和获得的最大价值。通过回溯的方式,从
dp数组中找到装入背包的物品。具体来说,从右下角开始遍历dp数组,如果当前位置的值不等于上一个状态的值,说明选择了第i个物品放入背包,输出i并更新背包容量j。然后,向左上方移动,继续遍历。最后,输出最大价值,即
dp[weight.length][a]的值。
🎃总代码:
package one;public class Value {public static void main(String[] args) {int[] weight = { 2, 2, 6, 5, 4 };int[] value = { 6, 3, 5, 4, 6 };int a = 10;int[][] dp = new int[weight.length + 1][a + 1];for (int i = 1; i <= weight.length; i++) {for (int j = 1; j <=a; j++) {if (j >= weight[i - 1]) {dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + value[i - 1]);} else {dp[i][j] = dp[i - 1][j];}}}System.out.print("装入的物品是第");int i = weight.length;int j = a;while (i > 0 && j > 0) {if (dp[i][j] != dp[i - 1][j]) {System.out.print(i + "个,");j -= weight[i - 1];}i--;}System.out.println("\n最大价值为:" + dp[weight.length][a]);}
}🎃运行截图:
💻three:
🎃问题:
最长公共子序列问题:求X={A,B,C,B,D,A,B}和Y={B,D,C,A,B,A}的最长公共子序列。
🎃解题思路:
最长公共子序列(Longest Common Subsequence,LCS)问题是经典的动态规划问题之一。给定两个序列 X 和 Y,找出它们的最长公共子序列的长度。
对于序列 X={A,B,C,B,D,A,B} 和 Y={B,D,C,A,B,A},可以采用动态规划的方法来解决最长公共子序列问题。下面是解题的思路和步骤:
定义状态: 创建一个二维数组
dp,其中dp[i][j]表示序列X的前i个元素与序列Y的前j个元素的最长公共子序列的长度。状态转移方程: 根据动态规划的性质,我们可以使用以下状态转移方程来计算
dp[i][j]:
- 如果
X[i-1] == Y[j-1],即序列X的第i-1个元素和序列Y的第j-1个元素相等,那么dp[i][j] = dp[i-1][j-1] + 1,表示当前这对匹配的字符可以贡献到最长公共子序列的长度中。- 如果
X[i-1] != Y[j-1],即序列X的第i-1个元素和序列Y的第j-1个元素不相等,那么dp[i][j] = max(dp[i-1][j], dp[i][j-1]),表示当前位置的最长公共子序列长度取决于去掉X的最后一个元素时和去掉Y的最后一个元素时哪个更长。初始化边界条件: 对于
dp数组的第一行和第一列,因为其中一个序列为空时,最长公共子序列的长度必定为 0,所以将其初始化为 0。填充表格: 根据状态转移方程,从
dp[0][0]开始,逐行或逐列填充dp数组,直到填满整个表格。回溯求解: 最后根据填充好的
dp数组,可以进行回溯来找到具体的最长公共子序列。通过以上步骤,就可以求解出序列 X 和 Y 的最长公共子序列的长度。希望这个解题思路能够帮助你理解如何使用动态规划来解决最长公共子序列问题。
🎃代码分析:
main 方法:
public static void main(String[] args) {// TODO Auto-generated method stubString X = "ABCBDAB";String Y = "BDCABA";int[][] C = LCSLength(X, Y);System.out.println("最长公共子序列长度为:" + C[X.length()][Y.length()]);System.out.print("最长公共子序列为:");printLCS(C, X, Y, X.length(), Y.length());}
- 在主方法中定义了两个字符串 X 和 Y,分别为 "ABCBDAB" 和 "BDCABA"。
- 创建一个二维数组 C,并调用 LCSLength 方法计算最长公共子序列的长度,并将结果存储在数组 C 中。
- 打印最长公共子序列的长度。
- 调用 printLCS 方法,传入数组 C、字符串 X、字符串 Y 以及字符串 X 和 Y 的长度,打印最长公共子序列。
LCSLength 方法:
public static int[][] LCSLength(String X, String Y) {int m = X.length();int n = Y.length();int[][] C = new int[m + 1][n + 1];for (int i = 0; i <= m; i++) {C[i][0] = 0;}for (int j = 0; j <= n; j++) {C[0][j] = 0;}for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {if (X.charAt(i - 1) == Y.charAt(j - 1)) {C[i][j] = C[i - 1][j - 1] + 1;} else {C[i][j] = Math.max(C[i - 1][j], C[i][j - 1]);}}}return C;}
- 此方法用于计算给定两个字符串 X 和 Y 的最长公共子序列的长度。
- 首先获取字符串 X 和 Y 的长度并创建一个大小为 (m+1) x (n+1) 的二维数组 C,其中 m 和 n 分别是字符串 X 和 Y 的长度。
- 初始化数组 C 的第一行和第一列为 0。
- 使用两个嵌套的 for 循环遍历字符串 X 和 Y 的所有组合。
- 如果 X.charAt(i-1) 等于 Y.charAt(j-1),则说明当前字符属于最长公共子序列,此时将 C[i][j] 设置为 C[i-1][j-1] + 1。
- 否则,根据动态规划的规则选择 C[i-1][j] 和 C[i][j-1] 中的较大值赋给 C[i][j]。
- 最后返回填充好的数组 C。
printLCS 方法:
public static void printLCS(int[][] C, String X, String Y, int i, int j) {if (i == 0 || j == 0) {return;}if (X.charAt(i - 1) == Y.charAt(j - 1)) {printLCS(C, X, Y, i - 1, j - 1);System.out.print(X.charAt(i - 1));} else if (C[i - 1][j] >= C[i][j - 1]) {printLCS(C, X, Y, i - 1, j);} else {printLCS(C, X, Y, i, j - 1);}}
- 此方法用于回溯求解最长公共子序列,并将其打印出来。
- 如果 i 或 j 为 0,则表示已经回溯到了边界,直接返回。
- 如果 X.charAt(i-1) 等于 Y.charAt(j-1),则说明当前字符属于最长公共子序列,递归调用 printLCS 方法继续向前找,并打印当前字符。
- 否则,根据动态规划的规则,如果 C[i-1][j] 大于等于 C[i][j-1],则递归调用 printLCS 方法向上找;否则,递归调用 printLCS 方法向左找。
🎃总代码:
package one;public class Sameple {public static void main(String[] args) {// TODO Auto-generated method stubString X = "ABCBDAB";String Y = "BDCABA";int[][] C = LCSLength(X, Y);System.out.println("最长公共子序列长度为:" + C[X.length()][Y.length()]);System.out.print("最长公共子序列为:");printLCS(C, X, Y, X.length(), Y.length());}public static int[][] LCSLength(String X, String Y) {int m = X.length();int n = Y.length();int[][] C = new int[m + 1][n + 1];for (int i = 0; i <= m; i++) {C[i][0] = 0;}for (int j = 0; j <= n; j++) {C[0][j] = 0;}for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {if (X.charAt(i - 1) == Y.charAt(j - 1)) {C[i][j] = C[i - 1][j - 1] + 1;} else {C[i][j] = Math.max(C[i - 1][j], C[i][j - 1]);}}}return C;}public static void printLCS(int[][] C, String X, String Y, int i, int j) {if (i == 0 || j == 0) {return;}if (X.charAt(i - 1) == Y.charAt(j - 1)) {printLCS(C, X, Y, i - 1, j - 1);System.out.print(X.charAt(i - 1));} else if (C[i - 1][j] >= C[i][j - 1]) {printLCS(C, X, Y, i - 1, j);} else {printLCS(C, X, Y, i, j - 1);}}
}
🎃运行截图:
🎯 做题方法总结:
动态规划(Dynamic Programming)是一种通过将问题划分为子问题并为子问题找到最优解来解决复杂问题的算法思想。它通常用于解决具有重叠子问题和最优子结构性质的问题。
以下是使用动态规划解决问题的一般步骤:
定义子问题: 确定问题可以被划分为若干个子问题。这些子问题通常与原问题相似,但规模较小。
建立状态转移方程: 定义问题的状态以及状态之间的关系。通过求解子问题,可以推导出原问题的解。
确定初始条件: 确定最小子问题的解,作为递归或迭代的起点。
填充表格或数组: 使用循环结构计算并填充数组或表格,以解决子问题。通常从最小子问题开始,逐步计算到原问题。
返回结果: 根据问题的要求,从填充的表格或数组中得出最终的结果。
下面是一个更具体的动态规划法解题的示例:
问题定义: 定义问题的具体要求。例如,求解最长公共子序列、最优路径、最大值等。
状态定义: 定义问题的状态。确定需要记录的信息,以及如何表示状态。
状态转移方程: 建立状态之间的关系。根据问题的性质和要求,确定状态之间的转移方式。
初始条件: 确定最小子问题的解,作为递归或迭代的起点。
计算顺序: 根据状态转移方程,确定计算子问题的顺序。通常从最小子问题开始,逐步计算到原问题。
填充表格或数组: 使用循环结构计算并填充数组或表格,以解决子问题。根据计算顺序,依次填充表格中的每个元素。
返回结果: 根据问题的要求,从填充的表格或数组中得出最终的结果。
需要注意的是,动态规划法适用于具有重叠子问题和最优子结构性质的问题。在实际应用中,可以根据具体问题的特点灵活运用动态规划思想,设计合适的状态和状态转移方程,以提高问题的求解效率。
相关文章:

【算法设计与分析】——动态规划算法
🎃个人专栏: 🐬 算法设计与分析:算法设计与分析_IT闫的博客-CSDN博客 🐳Java基础:Java基础_IT闫的博客-CSDN博客 🐋c语言:c语言_IT闫的博客-CSDN博客 🐟MySQL:…...
WPF组合控件TreeView+DataGrid之DataGrid封装
(关注博主后,在“粉丝专栏”,可免费阅读此文) wpf的功能非常强大,很多控件都是原生的,但是要使用TreeViewDataGrid的组合,就需要我们自己去封装实现。 我们需要的效果如图所示&#x…...

PIL/Pillow
Abstract PIL(Python Imaging Library)是一个用于图像处理的 Python 库。它提供了广泛的功能,包括图像加载、保存、调整大小、裁剪、旋转、滤镜应用等。 由于 PIL 的开发停止在 2009 年,因此推荐使用其后续的维护版本 Pillow。Pillow 是一个兼容 PIL 接…...

ARM 汇编入门
ARM 汇编入门 引言 ARM 汇编语言是 ARM 架构的汇编语言,用于直接控制 ARM 处理器。虽然现代软件开发更多地依赖于高级语言和编译器,但理解 ARM 汇编仍然对于深入了解系统、优化代码和进行低级调试非常重要。本文将为您提供一个简单的 ARM 汇编入门指南…...

SQL进阶:多表查询
在SQL基础部分,我们在讲解的过程中只用到了单表查询。但实际上,常见的业务场景单表查询不能满足,或者拆分查询性能过慢。这个时候我们就需要用到连接查询。即查询多表按一定规则合并后的数据。 注意,合并后的数据也是表ÿ…...
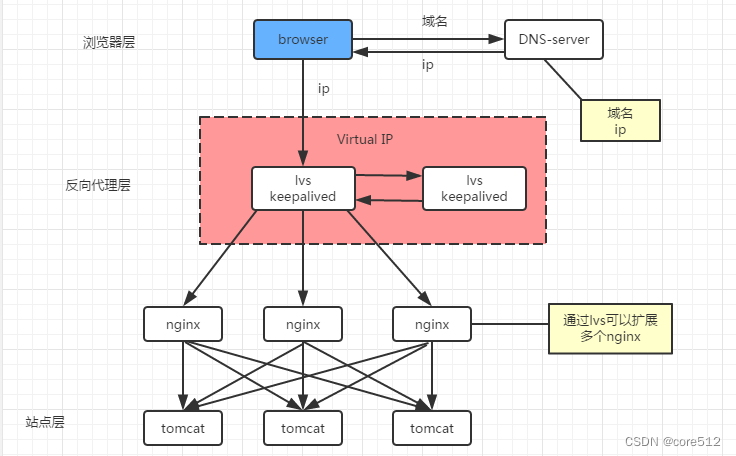
多层负载均衡实现
1、单节点负载均衡 1)站点层与浏览器层之间加入了一个反向代理层,利用高性能的nginx来做反向代理 2)nginx将http请求分发给后端多个web-server 优点: 1)DNS-server不需要动 2)负载均衡:通过ngi…...
Redis取最近10条记录
有时候我们有这样的需求,就是取最近10条数据展示,这些数据不需要存数据库,只用于暂时最近的10条,就没必要在用到Mysql类似的数据库,只需要用redis即可,这样既方便也快! 具体取最近10条的方法&a…...

Mybatis之增删改查
目录 一、引言 二、Mybatis——增 举例:添加用户 三、Mybatis——删 举例:删除用户 四、Mybatis——改 举例:修改用户 五、Mybatis——查 六、注意 END: 一、引言 书接上回,我们在了解完mybatis之后,肯…...

Go 代码检查工具 golangci-lint
一、介绍 golangci-lint 是一个代码检查工具的集合,聚集了多种 Go 代码检查工具,如 golint、go vet 等。 优点: 运行速度快可以集成到 vscode、goland 等开发工具中包含了非常多种代码检查器可以集成到 CI 中这是包含的代码检查器列表&…...

SwiftUI 趣谈之:绝不可能(Never)的 View!
概览 SwiftUI 的出现极大的解放了秃头码农们的生产力。SwiftUI 中众多原生和自定义视图对于我们创建精彩撩人的 App 功不可没! 不过,倘若小伙伴们略微留意过 SwiftUI 框架头文件里的源代码,就会发现里面嵌有一些奇怪 Never 类型,…...

etcd是什么
目录 1.关于etcd2.应用场景 本文主要介绍etcd 概念和基本应用场景。 1.关于etcd etcd是一个开源的、分布式的键值存储系统,用于共享配置和服务发现。它是由CoreOS团队开发的,主要用于实现分布式系统的配置管理和服务发现。 etcd的主要特性包括&#x…...

应用全局的UI状态存储AppStorage
目录 1、概述 2、StorageProp 2.1、观察变化和行为表现 3、StorageLink 3.1、观察变化和行为表现 4、从应用逻辑使用AppStorage和LocalStorage 5、从UI内部使用AppStorage和LocalStorage 6、不建议借助StorageLink的双向同步机制实现事件通知 6.1、推荐的事件通知方式…...

MySQL数据库 触发器
目录 触发器概述 语法 案例 触发器概述 触发器是与表有关的数据库对象,指在insert/update/delete之前(BEFORE)或之后(AFTER),触发并执行触发器中定义的soL语句集合。触发器的这种特性可以协助应用在数据库端确保数据的完整性,日志记录&am…...

C语言学习之给定任意的字符串,清除字符串中的空格
实例要求:给定任意的字符串,清除字符串中的空格,并将其输出;实例分析:1、指针函数实现,需要注意指针函数的返回值是一个指针类型;2、字符类型的数组实现,循环遍历并赋给新的数组&…...

由实验数据进行函数拟合的python实现
0.引言 已知公式求参的过程,对工程而言,一般是一个线性拟合或者非线性拟合的过程。我们现在来以代码片段为例,来描述如何求参。一般这个过程会涉及超定方程的计算。这个过程,原本需要使用matlab,现在python照样可以做…...

<JavaEE> 基于 UDP 的 Socket 通信模型
目录 一、认识相关API 1)DatagramSocket 2)DatagramPacket 3)InetSocketAddress 二、UDP数据报套接字通信模型概述 三、回显客户端-服务器通信 1)服务器代码 2)客户端代码 一、认识相关API 1)Data…...

Golang 链表的基础知识
文章目录 链表链表基础知识部分链表的存储方式链表的定义链表的操作性能分析 链表 更多有关于go链表的内容可以见这篇文章链表的创建和读取 链表基础知识部分 什么是链表,链表是一种通过指针串联在一起的线性结构,每一个节点由两部分组成,…...

webpack 常见面试题
1、什么是webpack(必会) webpack是一个打包模块化javascript的工具,在webpack里一切文件皆模块,通过loader转换文件,通过plugin注入钩子,最后输出由多个模块组合成的文件,webpack专注构建模块化…...

three.js实战模拟VR全景视图
文章中使用到的案例图片都来源于:Humus - Textures 里面有很多免费的资源,可以直接下载,每个资源里面都提供6个不同方位的图片,我们通过threejs稍微处理一下,就能实现以下3D效果的场景了。 <template><div …...

聊聊Spring Boot配置文件:优先级顺序、bootstrap.yml与application.yml区别详解
Spring Boot 配置文件 优先级顺序 在Spring Boot中,配置文件的优先级顺序是:bootstrap.yml > application.yml > application-{profile}.yml,其中 {profile} 表示不同的环境配置,如 dev、test、prod 等。当存在相同名称的…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...


