回溯算法 典型习题
vector<vector<int>> res;
vector<int> path;void dfs() {if (递归终止条件){res.push_back(path);return;}// 递归方向for (xxx) {path.push_back(val);dfs();path.pop_back();}
}1.涉及枚举
2.不确定 for 循环的次数
总结
枚举各种可能的情况。
0.直接枚举子集
1.约束条件是子集中数字的和 39
2.约束条件是子集的大小 77 46 47
3.约束条件是1 2两者的结合 2161
4.约束条件是集合数 + sum 93 698
5.去重:同层删去相同的递归起点
6.约束条件是 子集中数的大小关系 491
7.前一个情况可能是后一个情况的约束 51
77
第一层可以选 1 2 3 4
第二层可以选 234 134 ...
需要 path 存储选择的路径。需要 index 作为元素下标。
class Solution {
public:// 储存当前路径vector<int> path;vector<vector<int>> res;vector<vector<int>> combine(int n, int k) {dfs(1, n, k);return res;}void dfs(int index, int n, int k) {// 比如 k = 2, n = 4, index = 4// 不足以构成数组,要提前结束if (path.size() + (n - index + 1) < k) return;// 如果路径的长度是 k,那么把这个路径加入到结果数组if (path.size() == k) {res.push_back(path);return;}// 否则的话,从 index 开始回溯for (int i = index; i <= n; ++i) {path.push_back(i);dfs(i + 1, n, k);path.pop_back();}}
};39
target = 7
2 2 3/ 2 3 2
3 4
递归树:
s1 2 3 6 7
s2 2367 2367 ...
s3 2367 ...
这一次选了2,下一次从>=2开始选
class Solution {
public:vector<vector<int>> res;vector<int> path;vector<vector<int>> combinationSum(vector<int>& candidates, int target) {//先排序sort(candidates.begin(), candidates.end());// 从index = 0的位置开始选,一开始 sum = 0dfs(0, 0, candidates, target);return res;}void dfs(int index, int sum, vector<int>& candidates, int target) {if (sum >= target) {if (sum == target) {res.push_back(path);}return;}// 这次选了 index 下次从 index 开始选for (int i = index; i <= candidates.size() - 1; ++i) {if (sum + candidates[i] > target) return;path.push_back(candidates[i]);// 更新 sumdfs(i, sum + candidates[i], candidates, target);path.pop_back();}}
};40 同层去重
和39的区别是不能重复
# 模板
class Solution {
public:vector<vector<int>> res;vector<int> path;vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {sort(candidates.begin(), candidates.end());dfs(0, 0, candidates, target);return res;}void dfs(int index, int sum, vector<int>& candidates, int target) {if (sum >= target) {if (sum == target) {res.push_back(path);}return;}// 循环 + 递归for () {}}
};class Solution {
public:vector<vector<int>> res;vector<int> path;vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {sort(candidates.begin(), candidates.end());dfs(0, 0, candidates, target);return res;}void dfs(int index, int sum, vector<int>& candidates, int target) {if (sum >= target) {if (sum == target) {res.push_back(path);}return;}// 同层去重// 递归起点都是2,那么后面可以不必递归了unordered_set<int> occ;for (int i = index; i <= candidates.size() - 1; ++i) {if (occ.find(candidates[i]) != occ.end()) {continue;}occ.insert(candidates[i]);path.push_back(candidates[i]);dfs(i + 1, sum + candidates[i], candidates, target);path.pop_back();}}
};216 固定数据集
class Solution {
public:vector<vector<int>> res;vector<int> path;vector<vector<int>> combinationSum3(int k, int n) {dfs(1, 0, k, n);return res;}void dfs(int index, int sum, int k, int n) {if (sum >= n) {// 选 k 个数 和为 nif (sum == n && path.size() == k) {res.push_back(path);}}for (int i = index; i <= 9; ++i) {if (sum + i > n) {return;}path.push_back(i);dfs(i + 1, sum + i, k, n);path.pop_back();}}
};93 复原ip地址
遍历字符串长度
根据不同的长度截取子串
class Solution {
public:vector<string> res;vector<string> segMent;vector<string> restoreIpAddresses(string s) {segMent.resize(4);dfs(0, 0, segMent, s);return res;}bool check(string s) {// 要么是 0 要不是 0 开头的// 字符串转数字return (s[0] != '0' || s == "0") && stoi(s) < 256;}string toString(vector<string> &segMent) {string res;for (int i = 0; i < 3; ++i) {res += segMent[i];res += '.';}res += segMent[3];return res;}// void dfs(int index, int segId, vector<string> &segMent, string s){if (index == s.size() || segId == 4) {if (index == s.size() && segId == 4) {res.push_back(toString(segMent));}return;}for (int i = 1; i <= 3; ++i) {if (index +i > s.size()) return;string sub;// 从 index 开始截取长度为 isub = s.substr(index, i);if (check(sub)) {segMent[segId] = sub;dfs(index + i, segId + 1, segMent, s);}}}
};78 子集
123
path 初始为空
1 2 3
23 3 /
3/ /
某 index 数取完就从 index + 1 开始取
class Solution {
public:vector<vector<int>> res;vector<int> path;vector<vector<int>> subsets(vector<int>& nums) {dfs(0, nums);return res;}void dfs(int index, vector<int>& nums) {res.push_back(path);for (int i = index; i <= nums.size() - 1; ++i) {path.push_back(nums[i]);dfs(i + 1, nums);path.pop_back();}}
};491 非递增子序列
class Solution {
public:vector<vector<int>> res;vector<int> path;vector<vector<int>> findSubsequences(vector<int>& nums) {dfs(0, nums);return res;}unordered_set<int> appear;void dfs(int index, vector<int>& nums) {if (path.size() >= 2) {res.push_back(path);}// 同层去重 [4, 6, 6, 7]unordered_set<int> occ;for (int i = index; i <= nums.size() - 1; ++i) {// 确保当前的递归起点没被遍历过if (occ.find(nums[i]) != occ.end()) continue;occ.insert(nums[i]);// 确保序列一直保持递增if (path.size() > 0 && nums[i] < path.back()) continue;path.push_back(nums[i]);dfs(i + 1, nums);path.pop_back();}}
};46 全排列
每一次都是从头到尾遍历
class Solution {
public:vector<int> path;vector<int> used; // 将 vector<bool> 改为 vector<int>vector<vector<int>> res;vector<vector<int>> permute(vector<int>& nums) {used.resize(nums.size(), 0); // 初始化 used 向量dfs(nums);return res;}void dfs(vector<int>& nums) {if (path.size() == nums.size()) {res.push_back(path);return;}for (int i = 0; i < nums.size(); ++i) {// 如果数字没被用过则改为被用过,且更新pathif (!used[i]) {used[i] = 1; // 将 false 改为 1,表示已使用path.push_back(nums[i]);dfs(nums);path.pop_back();used[i] = 0; // 将 true 改为 0,表示未使用}}}
};
47 不重复全排列
和 46 不同的一点是,
[1,1,2] 会出现 [2,1,1] 两次,那么加一个hash去重
class Solution {
public:vector<vector<int>> res;vector<int> used;vector<int> path;vector<vector<int>> permuteUnique(vector<int>& nums) {used.resize(nums.size(), 0);dfs(nums);return res;}void dfs(vector<int>& nums) {if (path.size() == nums.size()) {res.push_back(path);return;}// 同层去重,去除递归起点相同的同层元素unordered_set<int> occ;for (int i = 0; i < nums.size() ; ++i) {if (!used[i] && (occ.find(nums[i]) == occ.end())) {used[i] = 1; // 将 false 改为 1,表示已使用path.push_back(nums[i]);dfs(nums);path.pop_back();used[i] = 0; // 将 true 改为 0,表示未使用}}}
};698 k 个等和子集
class Solution {
public:vector<int> subs;int ave;bool canPartitionKSubsets(vector<int>& nums, int k) {int sum = 0;// 桶subs.resize(k,0);// 求和sum = accumulate(nums.begin(), nums.end(), 0);// 是否能被 k 整除if (sum % k != 0) {return false;}ave = sum / k;// 先装大的//sort(nums.begin(), nums.end(), greater());sort(nums.begin(), nums.end(), greater());// 从 0 号位置开始return dfs(0, nums, k);}bool dfs(int index, vector<int>& nums, int k) {// 如果已经遍历完了所有数字// 查看每个子集大小if (index == nums.size()) {for (auto sub : subs) {if (sub != ave) {return false;}}return true;}// 对于同一个元素不要尝试和相同的子集unordered_set<int> occ;// 核心逻辑// 分 k 个桶,依次遍历,更新每个桶中元素的值,再 dfs// dfs 时依次选取不同的数字// 如果当前的桶再装入一个数字超过 ave// 去重for (int i = 0; i < k; ++i) {if (subs[i] + nums[index] > ave || occ.find(subs[i]) != occ.end()) continue;occ.insert(subs[i]);subs[i] += nums[index];if (dfs(index + 1, nums, k)) return true;subs[i] -= nums[index];}return false;}
};51 皇后
class Solution {
public:vector<vector<string>> solveNQueens(int n) {vector<bool> col(n, false);vector<bool> diag1(20, false);vector<bool> diag2(20, false);vector<int> queens(n, 0);dfs(0, col, diag1, diag2, queens, n);return res; // 返回结果集}private:vector<vector<string>> res; // 存储结果集// 深度优先搜索函数void dfs(int index, vector<bool>& col, vector<bool>& diag1, vector<bool>& diag2, vector<int>& queens, int n) {if (index == n) {res.push_back(generate(queens, n));return;}for (int i = 0; i < n; ++i) {if (col[i] || diag1[index + i] || diag2[index - i + 9]) continue;queens[index] = i;// 当前行第 i 列放置皇后col[i] = diag1[index + i] = diag2[index - i + 9] = true;dfs(index + 1, col, diag1, diag2, queens, n);col[i] = diag1[index + i] = diag2[index - i + 9] = false;}}// 生成棋盘vector<string> generate(vector<int>& queens, int n) {vector<string> board;for (int i = 0; i < n; ++i) {string row(n, '.');row[queens[i]] = 'Q';board.push_back(row);}return board; // 返回生成的棋盘}
};
汇编
链接
静态
相关文章:

回溯算法 典型习题
vector<vector<int>> res; vector<int> path;void dfs() {if (递归终止条件){res.push_back(path);return;}// 递归方向for (xxx) {path.push_back(val);dfs();path.pop_back();} } 1.涉及枚举 2.不确定 for 循环的次数 总结 枚举各种可能的情况。 0.直接…...

14. 从零用Rust编写正反向代理, HTTP文件服务器的实现过程及参数
wmproxy wmproxy是由Rust编写,已实现http/https代理,socks5代理, 反向代理,静态文件服务器,内网穿透,配置热更新等, 后续将实现websocket代理等,同时会将实现过程分享出来ÿ…...

【随笔】MD5加密字符串、文件apache、springframework实现
文章目录 一、引入依赖二、工具代码三、测试代码四、输出结果 一、引入依赖 commons-codec <dependency><groupId>commons-codec</groupId><artifactId>commons-codec</artifactId><version>1.13</version> </dependency>二…...
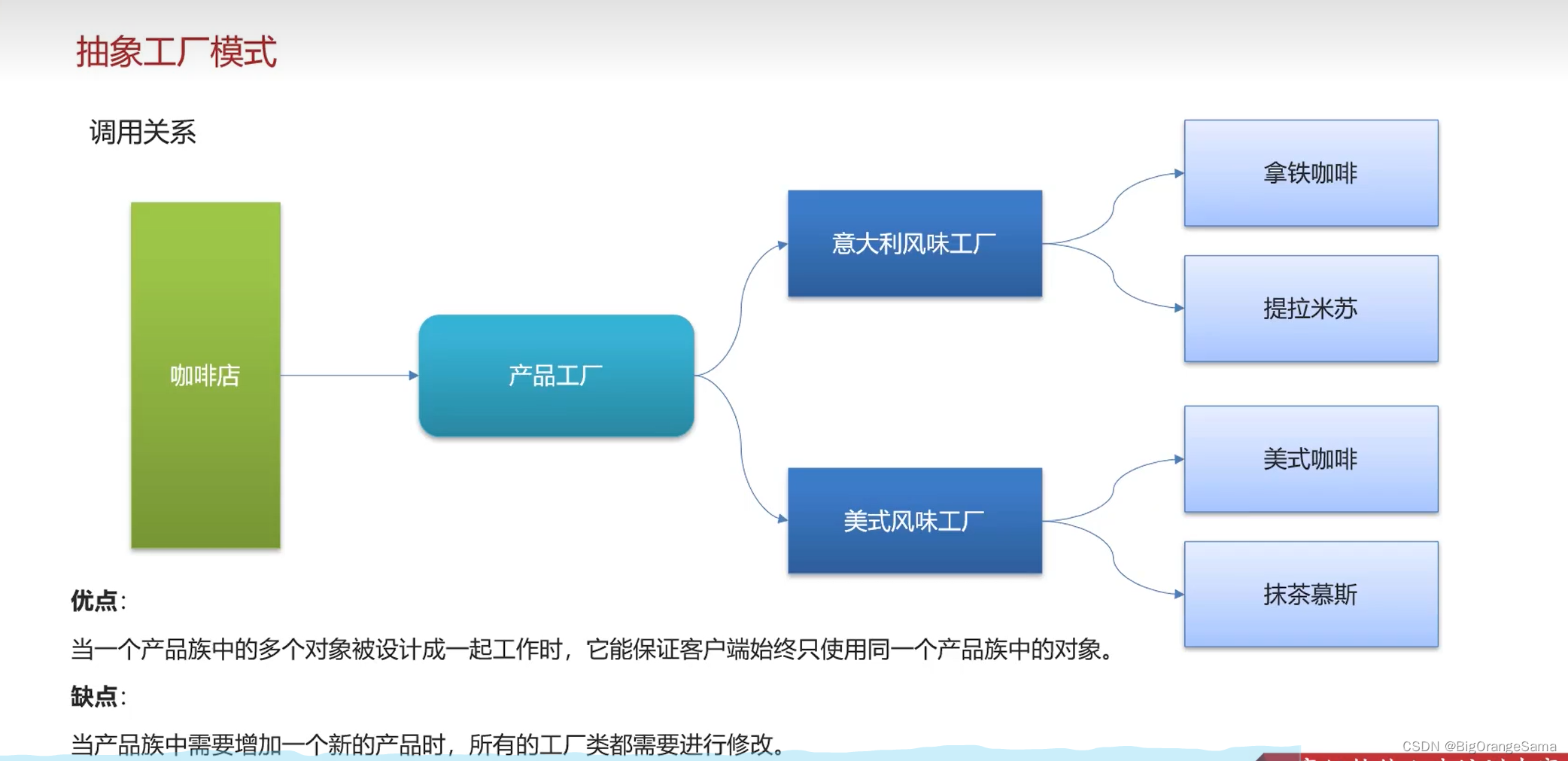
java八股 设计模式
企业场景篇-03-设计模式-工厂设计模式-工厂方法模式_哔哩哔哩_bilibili 1.简单工厂模式 新加咖啡类的时候需要在唯一的那个工厂类里加代码,这样就耦合了 2.工厂模式 相对于简单模式的一个工厂生产所有咖啡,这里只定义了一个抽象咖啡工厂,然…...

Docker安装(CentOS)+简单使用
Docker安装(CentOS) 一键卸载旧的 sudo yum remove docker* 一行代码(自动安装) 使用官方安装脚本 curl -fsSL https://get.docker.com | bash -s docker --mirror Aliyun 启动 docker并查看状态 运行镜像 hello-world docker run hello-world 简单使用 使用 docker run …...
)
Mybatis配置-环境配置(environments)
MyBatis支持配置多个环境,这有助于将您的SQL映射应用于多个数据库,无论出于何种原因。例如,您可能希望为开发、测试和生产环境使用不同的配置。或者,您可能有多个共享相同模式的生产数据库,并且想要在两者上使用相同的…...

Android模拟器的安装和adb连接
一、前置说明 APP 自动化可以使用真机进行测试,也可以使用模拟器来模拟安卓设备。我们可以根据个人喜好安装模拟器,个人推荐安装两款模拟器:网易 MuMu 模拟器、夜神模拟器。 MuMu模拟器可以支持 Android 12 版本,优点是…...

引领创新潮流,武汉灰京文化开创游戏行业新推广标杆
作为市场引领者,武汉灰京文化通过多渠道、多维度的市场推广手段,不仅助力游戏产品广泛传播,更为整个游戏行业树立了新的推广标杆。公司的成功经验为其他游戏发行商提供了有力的借鉴,推动了行业向更创新、更多元的方向发展。 引领…...

HTML5文档
目录 HTML5文档结构1.HTML5页面结构2.HTML5新增结构元素 HTML5新增页面元素1.hgroup标记2.figure标记与figcaption标记3.mark标记与time标记4.details标记与summary标记5.progress标记与meter标记6.input标记与datalist标记 HTML5文档结构 HTML5文档结构同样是由头部和主体两部…...

springboot实现发送邮件开箱即用
springboot实现发送邮件开箱即用 环境依赖包yml配置Service层Controller层测试 环境 jdk17 springboot版本3.2.1 依赖包 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-mail</artifactId><ver…...
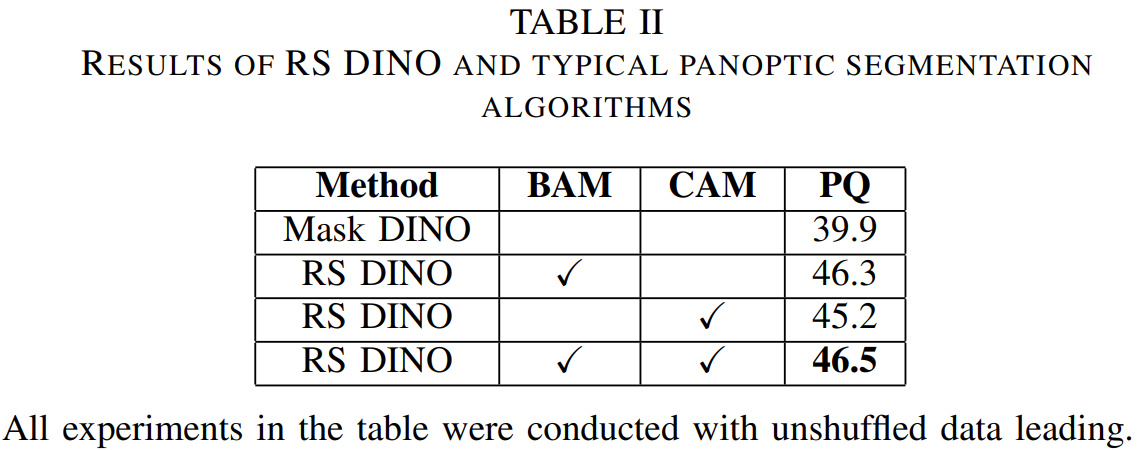
论文阅读——RS DINO
RS DINO: A Novel Panoptic Segmentation Algorithm for High Resolution Remote Sensing Images 基于MASKDINO模型,加了两个模块: BAM:Batch Attention Module 遥感图像切分的时候把一个建筑物整体比如飞机场切分到不同图片中,…...

【即插即用篇】YOLOv8改进实战 | 引入 Involution(内卷),用于视觉识别的新一代神经网络!涨点神器!
YOLOv8专栏导航:点击此处跳转 前言 YOLOv8 是由 YOLOv5 的发布者 Ultralytics 发布的最新版本的 YOLO。它可用于对象检测、分割、分类任务以及大型数据集的学习,并且可以在包括 CPU 和 GPU 在内的各种硬件上执行。 YOLOv8是一种尖端的、最先进的 (SOTA) 模型,它建立在以前成…...
在Excel中,如何简单快速地删除重复项,这里提供详细步骤
当你在Microsoft Excel中使用电子表格时,意外地复制了行,或者如果你正在制作其他几个电子表格的合成电子表格,你将遇到需要删除的重复行。这可能是一项非常无脑、重复、耗时的任务,但有几个技巧可以让它变得更简单。 删除重复项 …...

【Kafka-Eagle】EFAK告警配置与实践
Kafka-Eagle是一个开源的Kafka集群监控与告警系统,可以帮助用户实现对Kafka集群的实时监控、性能指标收集以及异常告警等功能。下面是关于Kafka-Eagle的告警配置和实践的一般步骤: 安装和配置Kafka-Eagle: 下载最新版本的Kafka-Eagle安装包&a…...
机器学习 | 概率图模型
见微知著,睹始知终。 见到细微的苗头就能预知事物的发展方向,能透过微小的现象看到事物的本质,推断结论或者结果。 概率模型为机器学习打开了一扇新的大门,将学习的任务转变为计算变量的概率分布。 实际情况中,各个变量…...

25、新加坡南洋理工、新加坡国立大学提出FBCNet:完美融合FBCSP的CNN,EEG解码SOTA水准![抱歉老师,我太想进步了!]
前言: 阴阳差错,因工作需要,需要查阅有关如何将FBCSP融入CNN中的文献,查阅全网,发现只此一篇文章,心中大喜,心想作者哪家单位,读之,原来是自己大导(新加坡工…...

单调栈分类、封装和总结
作者推荐 map|动态规划|单调栈|LeetCode975:奇偶跳 通过枚举最小(最大)值不重复、不遗漏枚举所有子数组 C算法:美丽塔O(n)解法单调栈左右寻找第一个小于maxHeight[i]的left,right,[left,right]直接的高度都是maxHeight[i] 可以…...

【Amazon 实验①】使用 Amazon CloudFront加速Web内容分发
文章目录 实验架构图1. 准备实验环境2. 创建CloudFront分配、配置动、静态资源分发2.1 创建CloudFront分配,添加S3作为静态资源源站2.2 为CloudFront分配添加动态源站 在本实验——使用CloudFront进行全站加速中,将了解与学习Amazon CloudFront服务&…...

<math.h> 头文件:C语言数学库函数
文章目录 概述基本算术运算sqrt()fabs()pow() 三角函数sin()cos() 对数函数log()log10() 指数函数exp() 其他函数ceil()floor() 结语 概述 math.h 是C语言标准库中的头文件,提供了许多与数学运算相关的函数。在本文中,我们将深入讨论一些 math.h 中常用…...

1.CentOS7网络配置
CentOS7网络配置 查看网络配置信息 ip addr 或者 ifconfig 修改网卡配置信息 vim /etc/sysconfig/network-scripts/ifcfg-ens192 设备类型:TYPEEthernet地址分配模式:BOOTPROTOstatic网卡名称:NAMEens192是否启动:ONBOOTye…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...
