java8实战 lambda表达式、函数式接口、方法引用双冒号(中)
前言
书接上文,上一篇博客讲到了lambda表达式的应用场景,本篇接着将java8实战第三章的总结。建议读者先看第一篇博客
其他函数式接口例子
上一篇有讲到Java API也有其他的函数式接口,书里也举了2个例子,一个是java.util.function.Consumer<T>, 定义了accpet抽象方法,接受泛型T对象,没有返回,一个是java.util.function.Function<T,R>,定义了apply方法,接受一个泛型T对象,返回泛型R对象
用consumer模拟forEach方法
@FunctionalInterface
public interface Consumer<T>{void accept(T t);
}
public static <T> void forEach(List<T> list, Consumer<T> c){\for(T i: list) {c.accept(i);}
}
forEach(Arrays.asList(1,2,3,4,5),(Integer i)->System.out.println(i));用Function来模拟map方法
@FunctionalInterface
public interface Function<T, R>{R apply(T t);
}
public static <T, R> List<R> map(List<T> list, Function<T, R> f){\List<R> result = new ArrayList<>();for(T s:list){result.add(f.apply(s));}return result;
}
List<Integer> l=map( Arrays.asList("lambdas","in","action"), (String s)->s.length());常用的函数式接口
因为很多泛型函数式接口,如Predicate<T>,Consumer<T>, 其中T只能绑定要引用类型(如Byte,Integer,Object),不能绑定到原始类型(如int,double,byte,char),所以最后一栏有原始类型特化,对比一下例子:
也就是说IntPredicate是当T=int原始类型的特殊情况。
public interface IntPredicate{boolean test(int t);
}IntPredicate evenNumbers = (int i) -> i % 2 == 0;evenNumbers.test(1000);Predicate<Integer> oddNumbers = (Integer i) -> i % 2 == 1;oddNumbers.test(1000);
lambda及函数式接口例子

异常捕获的处理
由于任何函数式接口都不允许抛出受检异常,所以需要在lambda表达式抛出异常,如:
Function<BufferedReader, String> f = (BufferedReader b) -> {try{return b.readline();}catch(IOException e) {throw new RuntimeException(e);}}使用局部变量
lambda可以没有限制地捕获实例变量和静态变量,但是局部变量必须显式声明为final或者事实上是final,如,下面代码无法编译,因为portNumber变量被赋值两次:
int portNumber = 1337;
Runnable r = () -> System.out.println(portnumber);
portNumber = 31337;这一限制其实背后是因为实例变量是存储在堆上,而局部变量是保持在栈上,如果lambda可以直接访问局部变量,而且lambda是在一个线程中使用的,则使用lambda的线程,可能会在分配该变量的线程将这个变量收回以后,去访问该变量。
方法引用
inventory.sort(Apple a1, Apple a2) -> a1.getWeight().compareTo(a2.getWeight());//使用方法引用
inventory.sort(comparing(Apple::getWeight));实际上方法引用是lambda的一种快捷写法,基本思想就是,如果一个lambda代表只是“直接调用这个方法”,那么最好还是用名称去调用它,而不是去描述如何调用它。
直观一点,可以认为:
Apple::getWeight 等于 (Apple a) -> a.getWeight()书本也举了一些例子

总结:方法引用就是lambda只调用特定方法时候一种快捷写法,上述的例子中lambda主体只有调用一个函数。
如何构建方法引用
方法引用有三类
1.指向静态方法的方法引用(如Integer的parseInt方法,写作Integer::parseInt)
2.指向任意类型实例方法的方法引用(如string的length方法,写作String::length)
3.指向现有对象的实例方法的方法引用(假设有一个局部变量expensiveTransaction用于存放Transanction类型的对象,它支持实例方法getValue, 那么你就可以写expensiveTransaction::getValue)
书中还有图来表达这三类: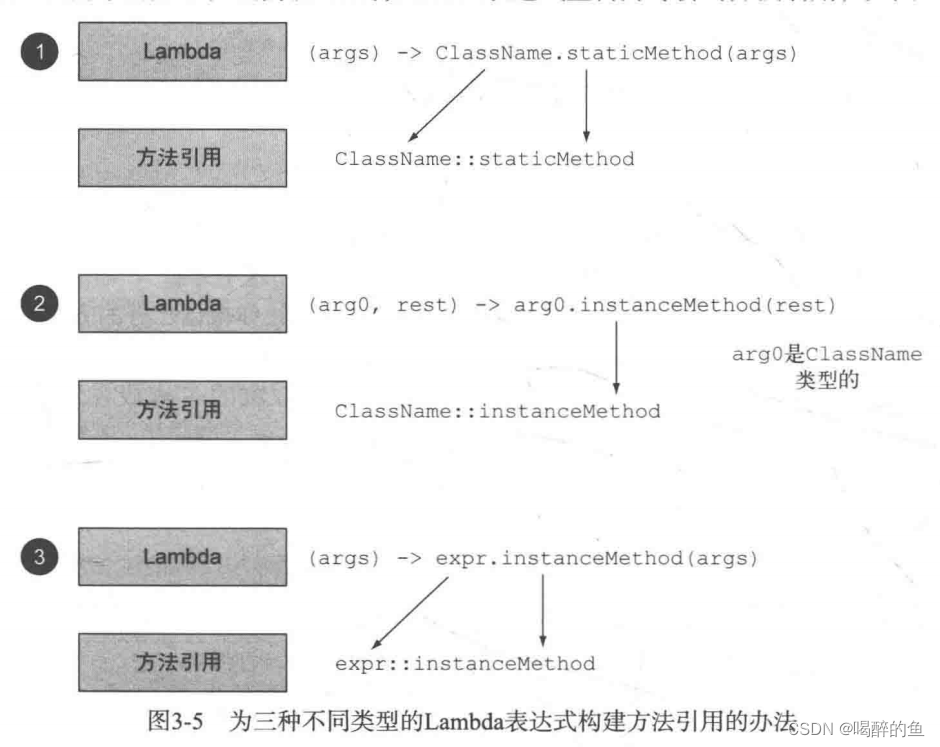
构造函数引用
对于一个现有构造函数,可以利用它的名称和关键字new来创建它的一个应用:ClassName::new,它的功能与指向静态方法的引用类似。假设一个构造函数没有参数,适合Supplier的签名()->Apple
Supplier<Apple> c1 = Apple::new; //指向默认Apple()的构造函数
Apple a1 = c1.get(); //产生一个新的apple等价于Supplier<Apple> c1 = () -> new Apple();
Apple a1 = c1.get(); //产生一个新的apple
如果构造函数是Apple(Integer weight), 那么它就适合Function接口的签名
Function<Integer, Apple> c2 = Apple::new; //指向Apple(Integer weight)的构造函数
Apple a2 = c2.apply(110); //输入重量产生一个新的apple等价于Function<Integer Apple> c2 = (weight) -> new Apple(weight);
Apple a2 = c2.get(); //产生一个新的apple
以此类推,如果有两个参数,就可以用BiFunction接口,那么如果多个参数,那么就需要自己构造了,可以参考第一篇的构造一个接口。
最后有个有趣的应用,将上面知识点串在一起,比如说给定一个水果名称和重量,创建一个水果的实例,我个人想到最简单粗暴的方式,写if/else语句,判断水果名称,然后就是new不同的水果,当然也可以结合上面知识点,将new这个起始动作(还没new)放在map中,实际要用时候再apply.
static Map<String, Function<Integer, Fruit>> map = new HashMap<>();
static {map.put("apple", Apple::new);map.put("orange", Orange::new);
//etc...
}public static Fruit giveMeFruit(String fruit, Integer weight) {return map.get(fruit.toLowerCase()).apply(weight);
}第三章还有最后的实战部分,放到最后一篇讲。
参考文献:
《java8 实战》
相关文章:

java8实战 lambda表达式、函数式接口、方法引用双冒号(中)
前言 书接上文,上一篇博客讲到了lambda表达式的应用场景,本篇接着将java8实战第三章的总结。建议读者先看第一篇博客 其他函数式接口例子 上一篇有讲到Java API也有其他的函数式接口,书里也举了2个例子,一个是java.util.functi…...

FPGA高端项目:UltraScale GTH + SDI 视频编解码,SDI无缓存回环输出,提供2套工程源码和技术支持
目录 1、前言免责声明 2、相关方案推荐我这里已有的 GT 高速接口解决方案我目前已有的SDI编解码方案 3、详细设计方案设计框图3G-SDI摄像头LMH0384均衡EQUltraScale GTH 的SDI模式应用UltraScale GTH 基本结构参考时钟的选择和分配UltraScale GTH 发送和接收处理流程UltraScale…...

为什么react call api in cDidMount
为什么react call api in cDM 首先,放到constructor或者cWillMount不是语法错误 参考1 参考2 根据上2个参考,总结为: 1、官网就是这么建议的: 2、17版本后的react 由于fiber的出现导致 cWM 会调用多次! cWM 方法已…...

openGauss学习笔记-171 openGauss 数据库运维-备份与恢复-导入数据-深层复制
文章目录 openGauss学习笔记-171 openGauss 数据库运维-备份与恢复-导入数据-深层复制171.1 使用CREATE TABLE执行深层复制171.1.1 操作步骤 171.2 使用CREATE TABLE LIKE执行深层复制171.2.1 操作步骤 171.3 通过创建临时表并截断原始表来执行深层复制171.3.1 操作步骤 openGa…...

[kubernetes]控制平面ETCD
什么是ETCD CoreOS基于Raft开发的分布式key-value存储,可用于服务发现、共享配置以及一致性保障(如数据库选主、分布式锁等)etcd像是专门为集群环境的服务发现和注册而设计,它提供了数据TTL失效、数据改变监视、多值、目录监听、…...

序列化类的高级用法
1.3.3 模型类序列化器 如果我们想要使用序列化器对应的是Django的模型类,DRF为我们提供了ModelSerializer模型类序列化器来帮助我们快速创建一个Serializer类。 ModelSerializer与常规的Serializer相同,但提供了: 基于模型类自动生成一系列…...
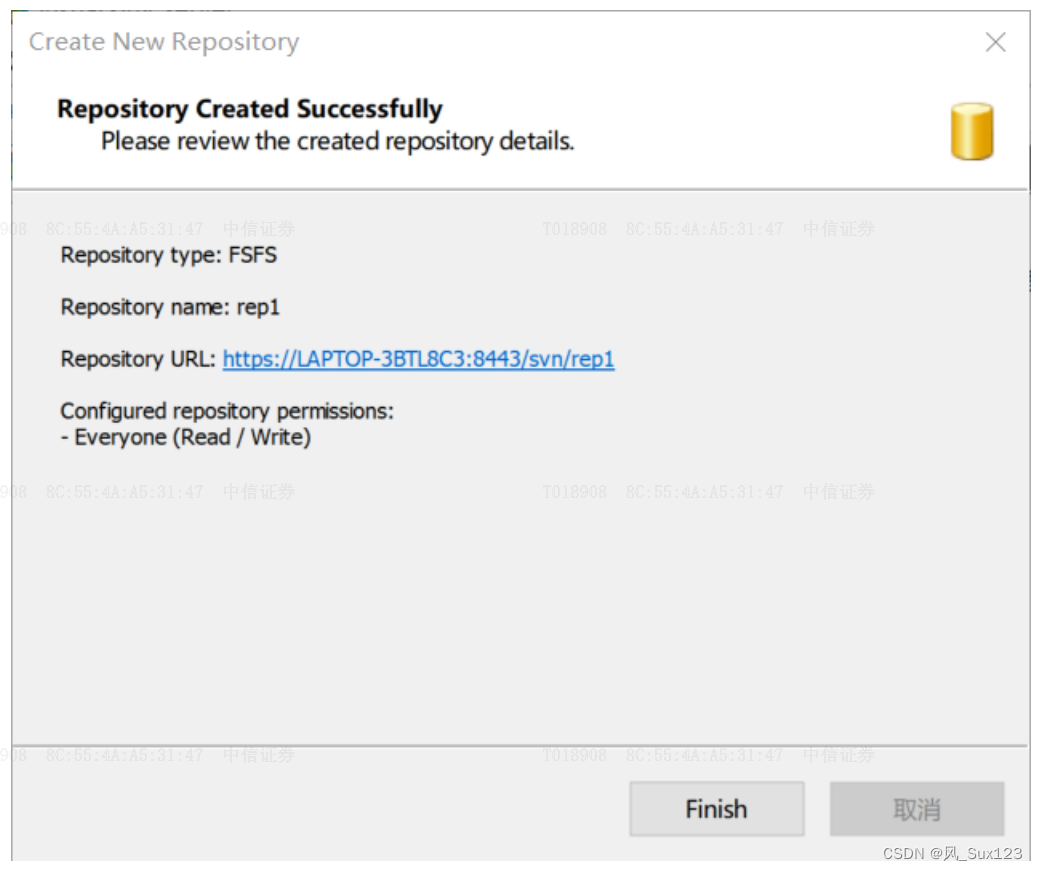
4.svn版本管理工具使用
1. 什么是SVN 版本控制 它可以记录每一次文件和目录的修改情况,这样就可以借此将数据恢复到以前的版本,并可以查看数据的更改细节! Subversion(简称SVN)是一个自由开源的版本控制系统。在Subversion管理下,文件和目录可以超越时空 SVN的优势 统一的版本号 Subversi…...

ZKP Algorithms for Efficient Cryptographic Operations 1 (MSM Pippenger)
MIT IAP 2023 Modern Zero Knowledge Cryptography课程笔记 Lecture 6: Algorithms for Efficient Cryptographic Operations (Jason Morton) Multi-scalar Multiplication(MSM) Naive: nP (((P P) P) P)… (2(2P))…Binary expand $n e_0e_1\alphae_2\alpha2\dots\e_{\…...
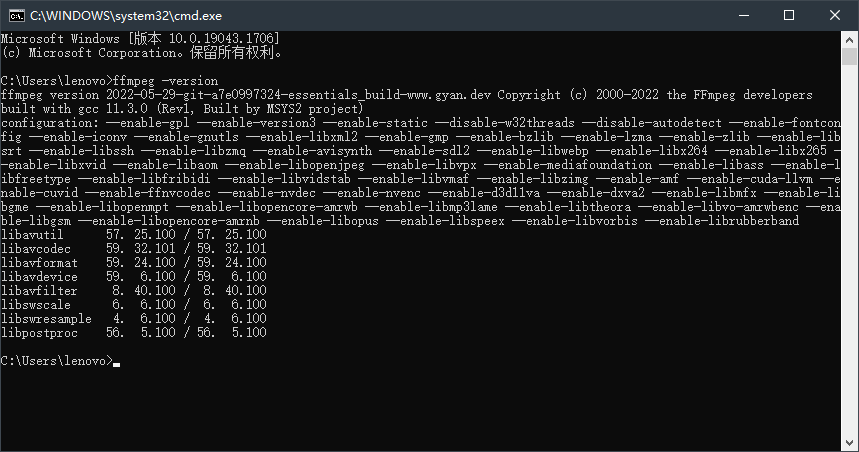
Windows系统安装 ffmpeg
下载及解压 ffmpeg官方下载地址:https://ffmpeg.org/download.html 下载好后将其解压至你想保存的位置中。 环境变量设置 打开Windows设置,在搜索框输入:系统高级设置。 新建环境变量,并输入bin目录具体位置。 安装检查 按住 w…...
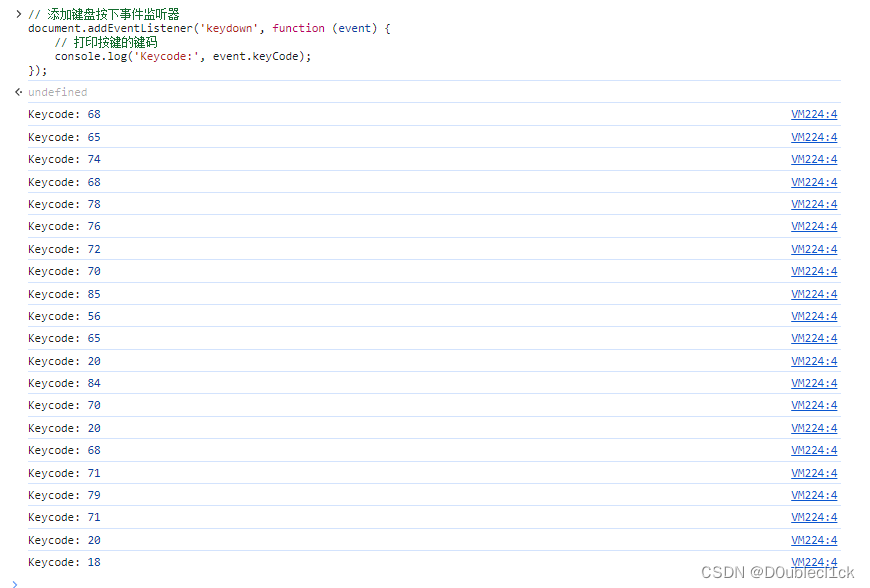
油猴脚本教程案例【键盘监听】-编写 ChatGPT 快捷键优化
文章目录 1. 元数据namenamespaceversiondescriptionauthormatchgranticon 2. 编写函数.1 函数功能2.1.1. input - 聚焦发言框2.1.2. stop - 取消回答2.1.3. newFunction - 开启新窗口2.1.4. scroll - 回到底部 3. 监听键盘事件3.1 监听X - 开启新对话3.2 监听Z - 取消回答3.3 …...

数据结构 | 查漏补缺
目录 数据的基本单位 冒泡排序 DFS和BFS中文 Prim 比较 中序线索二叉树 顺序栈 链栈 时间复杂度 循环队列 求第K个结点的值 数据的基本单位 数据元素 循环队列sq中,用数组elem[0‥25]存放数据元素,设当前sq->front为20,sq-&g…...

回溯算法练习题
78. 子集 中等 1.9K 相关企业 给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。 解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。 示例 1: 输入:nums [1,2,3] 输出&#x…...

代码随想录算法训练营 | day60 单调栈 84.柱状图中最大的矩形
刷题 84.柱状图中最大的矩形 题目链接 | 文章讲解 | 视频讲解 题目:给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。 求在该柱状图中,能够勾勒出来的矩形的最大面积。 1 < heights.len…...
vscode中vue项目报错
当在vscode中写代码时,报错报错报错......... 已经头大,还没写就报错, 这是因为eslint对语法的要求太过严格导致的编译时,出现各种语法格式错误 我们打开vue.config.js,加上这句代码,就OK啦 lintOnSave:…...
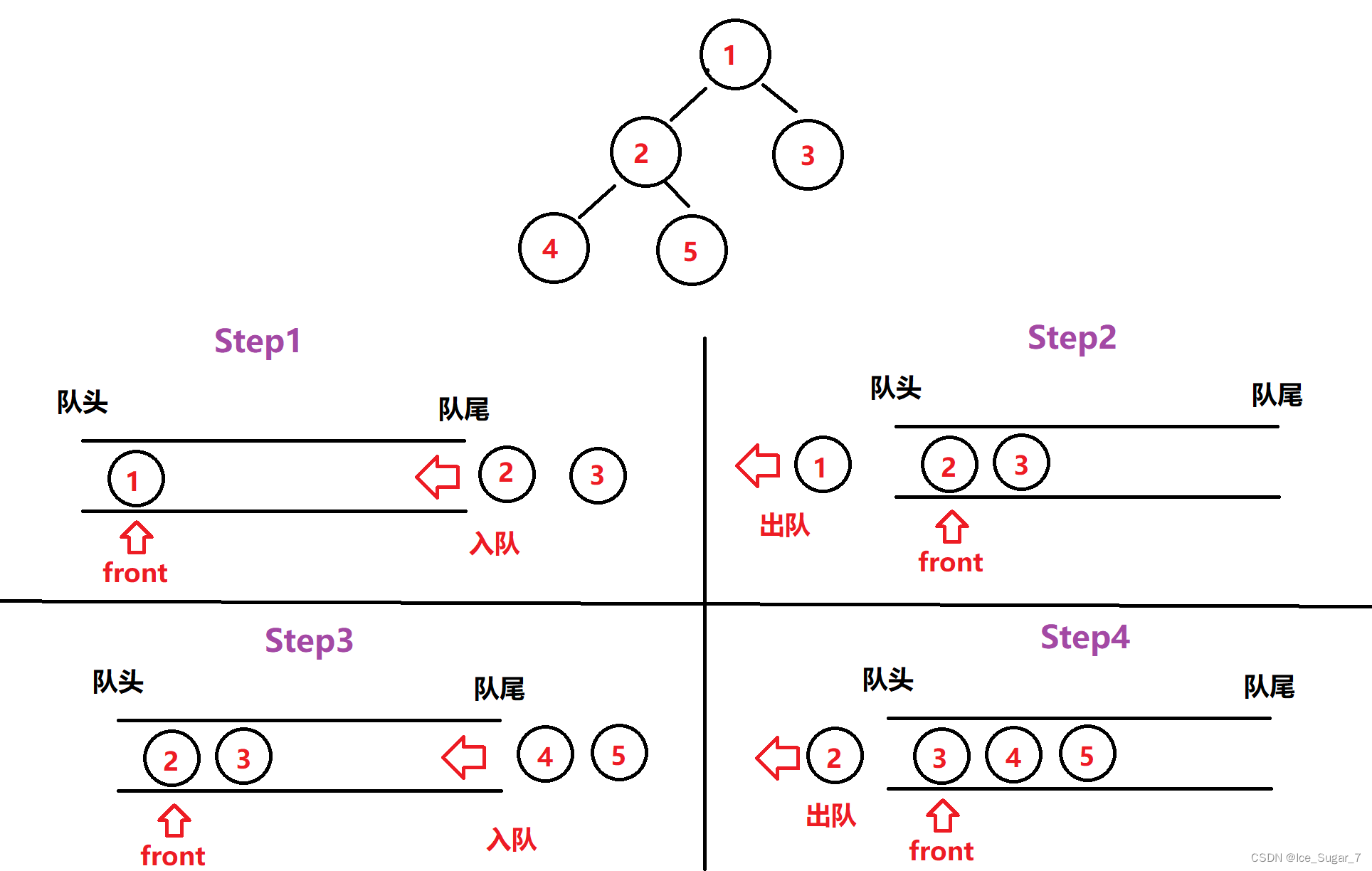
「数据结构」二叉树2
🎇个人主页:Ice_Sugar_7 🎇所属专栏:初阶数据结构 🎇欢迎点赞收藏加关注哦! 文章目录 🍉前言🍉链式结构🍉遍历二叉树🍌前序遍历🍌中序遍历&#x…...

数据处理系列课程 01:谈谈数据处理在数据分析中的重要性
一、数据分析 可能很多朋友第一次听到这个名词,那么我们先来谈一谈什么是数据分析。 数据分析是指用适当的统计分析方法对收集来的大量数据进行分析,将它们加以汇总和理解,以求最大化地开发数据的功能,发挥数据的作用。数据分析是…...

C++卡码网题目55--右旋字符串
卡码网题目链接 字符串的右旋转操作是把字符串尾部的若干个字符转移到字符串的前面。给定一个字符串 s 和一个正整数 k,请编写一个函数,将字符串中的后面 k 个字符移到字符串的前面,实现字符串的右旋转操作。 例如,对于输入字符…...
)
八股文打卡day8——计算机网络(8)
面试题:什么是强缓存和协商缓存? 我的回答: 强缓存:浏览器不需要发送请求到服务器,直接从浏览器缓存中获取数据。浏览器不需要和服务器进行交互就可以获取数据,这样极大提高了页面访问速度。 协商缓存&am…...

亚马逊推出 Graviton4:具有 536.7 GBps 内存带宽的 96 核 ARM CPU
如今,许多云服务提供商都设计自己的芯片,但亚马逊网络服务 (AWS) 开始领先于竞争对手,目前其子公司 Annapurna Labs 开发的处理器可以与 AMD 和英特尔的处理器竞争。本周,AWS 推出了 Graviton4 SoC,这是一款基于 ARM 的…...

跨域问题的解决
1.什么是跨域? 浏览器从一个域名的网页去请求另外一个域名的资源时,域名、端口或者协议不同都是跨域 2.跨域的解决方案 设置CORS响应头∶后端可以在HTTP响应头中添加相关的CORS标头,允许特定的源(域名、协议、端口)访问资源。S…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

