2016年第五届数学建模国际赛小美赛B题直达地铁线路解题全过程文档及程序
2016年第五届数学建模国际赛小美赛
B题 直达地铁线路
原题再现:
在目前的大都市地铁网络中,在两个相距遥远的车站之间运送乘客通常需要很长时间。我们可以建议在两个长途车站之间设置直达班车,以节省长途乘客的时间。
第一部分:请制定一个数学框架来优化终点站的选择,并评估建议的预期结果。
第二部分。如果你调整列车间隔或修建直达专线,探索你在经济和社会效益方面可能取得的任何优势。
第三部分给你所在城市的市长写一封两页的信,总结你的分析。把你的火车时刻表写在信的第二页。
整体求解过程概述(摘要)
本文对影响地铁两站间直达站设置的各个因素进行了模型研究。然后,我们可以确定是否建立一个直接的地铁站之间的两个遥远的车站。如果有必要,我们会对其进行优化。接下来,以北京为例。通过确定路线,给出了在社会经济等多种因素影响下的最佳发车时间。
模型一。首先,采用控制变量法,分析了地铁乘客的个人情况、时间和周围环境对客流的影响。然后利用logit模型对拟合结果进行验证。得出结论:处于工人阶级中间的年轻人经常出现的地区,如工业区、行政区、交通枢纽等,客流最大。通过对北京地铁线路距离的获取,利用数据平均法研究了距离对位置的影响,得出当两站点间直线距离大于15km时,应考虑建立直达地铁。
模型二。基于模型1的结论,采用Floyd算法计算客流和两地距离对地铁位置的影响。发现它们之间的关系成为正态分布和最高点两个站点,其中需要建立地铁直达的站点最好。并以北京市为例,利用该结论得出了首都国际机场3号航站楼地铁站到回龙观地铁站的直达线路。
模型三。通过遗传分析,利用MATLAB对模型二确定的北京线位置进行优化。最后,我们知道当地铁站位于隆泽和回龙观之间时,这个站点是最好的选择。
模型四。通过查阅相关文献,分析了首都国际机场3号航站楼地铁站至回龙观地铁站直达线路的社会效益、经济效益和旅客时间效益。将主成分分析与实证分析相结合,得出不同时段地铁发车间隔时间不同的结论。地铁的运行时间是6:00-23:45。在6:00-10:00和16:00-20:00,每10分钟一班,其余时间15分钟一班。
综上所述,当两站点之间的直线距离大于15km时,尤其是交通枢纽、工业区和行政区,且高峰时段最需要短间隔时间时,应考虑建立直达地铁。
模型假设:
1、不考虑地铁停车系统的需要。
2、假设两个长途车站之间的直达地铁对其他地铁系统没有影响。
3、假设地铁网络的一致性对地铁模型没有影响。
4、假定场地交通功能对本文构建的地铁模型无影响。
5、假设项目成本、效益、技术可行性等因素对第一部分模型无影响6、假设地铁始终准时,不会因外部因素造成延误。
问题重述:
为什么需要在两个相距较远的车站之间更换线路
在目前大城市的地铁网络中,在两个相距较远的车站之间运送乘客通常需要很长的时间。我们可以建议在两个长途车站之间设置直达班车,以节省长途旅客的时间。
我们需要解决的问题
1。如何建立一个数学框架来优化终端站的选择?如何评价最佳建议的预期效果?
2、如何调整列车间隔或建设直达专用线,发挥其经济效益和社会效益?
3、偿付能力如何处理?
写一封两页的信给市长,总结我们的分析,简要描述我们的设计特点和优势。
模型的建立与求解整体论文缩略图


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分程序代码:(代码和文档not free)
function m_main()
clear
clc
Max_gen = 100;
pop_size = 100;
chromsome = 10;
pc = 0.9;
pm = 0.25;
gen = 0;
init = 40*rand(pop_size, chromsome)-20;
pop = init;
fit = obj_fitness(pop);
[max_fit, index_max] = max(fit);
maxfit = max_fit;
[min_fit, index_min] = min(fit);
best_indiv = pop(index_max, :);
while gen<Max_gen
gen = gen+1;
bt(gen) = max_fit;
if maxfit<max_fit;
maxfit = max_fit;
pop(index_min, :) = pop(index_max, :);
best_indiv = pop(index_max, :);
end
best_indiv_tmp(gen) = pop(index_max);
newpop = ga(pop, pc, pm, chromsome, fit);
fit = obj_fitness(newpop);
[max_fit, index_max] = max(fit);
[min_fit, index_min] = min(fit);
pop = newpop;
trace(1, gen) = max_fit;
trace(2, gen) = sum(fit)./length(fit);
end
[f_max gen_ct] = max(bt)
maxfit
best_indiv
hold on
plot(trace(1, :), '.g:');
plot( trace(2, :), '.r-');
title('The experimental results in figure')
xlabel('The number of iterations/generation'), ylabel('The optimal structural');plot(gen_ct-1, 0:0.1:f_max+1, 'c-');
text(gen_ct, f_max+1, 'The maximum')
hold off
function [fitness] = obj_fitness(pop)
[r c] = size(pop);
x = pop;
fitness = zeros(r, 1);
for i = 1:r
for j = 1:c
fitness(i,1) = fitness(i, 1)+sin(sqrt(abs(40*x(i))))+1-abs(x(i))/20.0;
end
end
end
function newpop = ga(pop, pc, pm, chromsome, fit)
pop_size = size(pop, 1);
ps = fit/sum(fit);
pscum = cumsum(ps);%size(pscum)
r = rand(1, pop_size);
qw = pscum*ones(1, pop_size);
selected = sum(pscum*ones(1, pop_size)<ones(pop_size, 1)*r)+1;
newpop = pop(selected, :);
if pop_size/2 ~= 0
pop_size = pop_size-1;
end
for i = 1:2:pop_size-1
while pc>rand
c_pt = round(8*rand+1);
pop_tp1 = newpop(i, :);pop_tp2 = newpop(i+1, :);
newpop(i+1, 1:c_pt) = pop_tp1(1, 1:c_pt);
newpop(i, c_pt+1:chromsome) = pop_tp2(1, c_pt+1:chromsome);
end
end
for i = 1:pop_size
if pm>rand
m_pt = 1+round(9*rand);
newpop(i, m_pt) = 40*rand-20;
end
end
end
end
f_max =
19.7139
gen_ct =
32
maxfit =
19.7139
best_indiv =
0.0804 -9.8254 -1.1084 19.7403 -8.1866 -13.6728 -17.6449 3.7018
-15.0008 8.797
function Z=drawGaussian(u,v,x,y)
% u,vector,expactation;v,covariance matrix
%x=150:0.5:190;
%y=35:110;
[X,Y]=meshgrid(x,y);
DX=v(1,1);
dx=sqrt(DX);
DY=v(2,2);
dy=sqrt(DY);
COV=v(1,2);
r=COV/(dx*dy);
part1=1/(2*pi*dx*dy*sqrt(1-r^2));
p1=-1/(2*(1-r^2));
px=(X-u(1)).^2./DX;
py=(Y-u(2)).^2./DY;
pxy=2*r.*(X-u(1)).*(Y-u(2))./(dx*dy);
Z=part1*exp(p1*(px-pxy+py));
mesh(x,y,Z);
全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
相关文章:

2016年第五届数学建模国际赛小美赛B题直达地铁线路解题全过程文档及程序
2016年第五届数学建模国际赛小美赛 B题 直达地铁线路 原题再现: 在目前的大都市地铁网络中,在两个相距遥远的车站之间运送乘客通常需要很长时间。我们可以建议在两个长途车站之间设置直达班车,以节省长途乘客的时间。 第一部分…...

三秦通ETC续航改造
前些天开车时ETC每隔2分钟滴滴响一下,重插卡提示电池电压低 2.8V。看来应该是电池不行了。去银行更换ETC应该是需要费用的。还有一种办法是注销掉,然后去别的银行办一个。不过我想自己更换电池试一下。 首先拆下ETC,我使用的办法是开水烫。烧…...
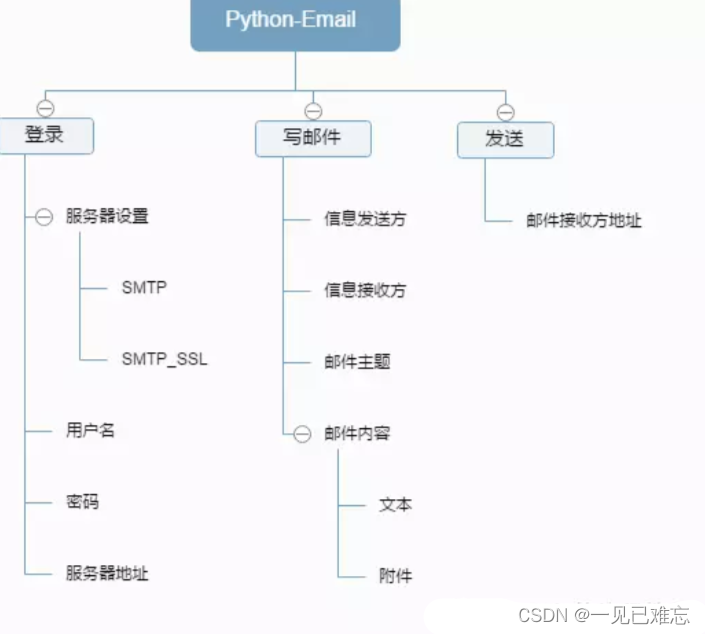
使用Python实现发送Email电子邮件【第19篇—python发邮件】
文章目录 👽使用Python实现发送Email电子邮件🎶实现原理🏃Python实现发送Email电子邮件-基础版👫实现源码🙆源码解析 💇Python实现发送Email电子邮件-完善版👫实现源码🙆源码解析&am…...

Docker基本命令和Docker怎么自己制作镜像
基本命令 启动新的容器(指定容器名称和端口映射【主机端口:容器端口】) docker run --name 容器名 -p 8080:80 镜像名 启动新的容器(交互式) docker run -it centos7-with-jdk /bin/bash 特权方式启动容器 docker run -d --…...
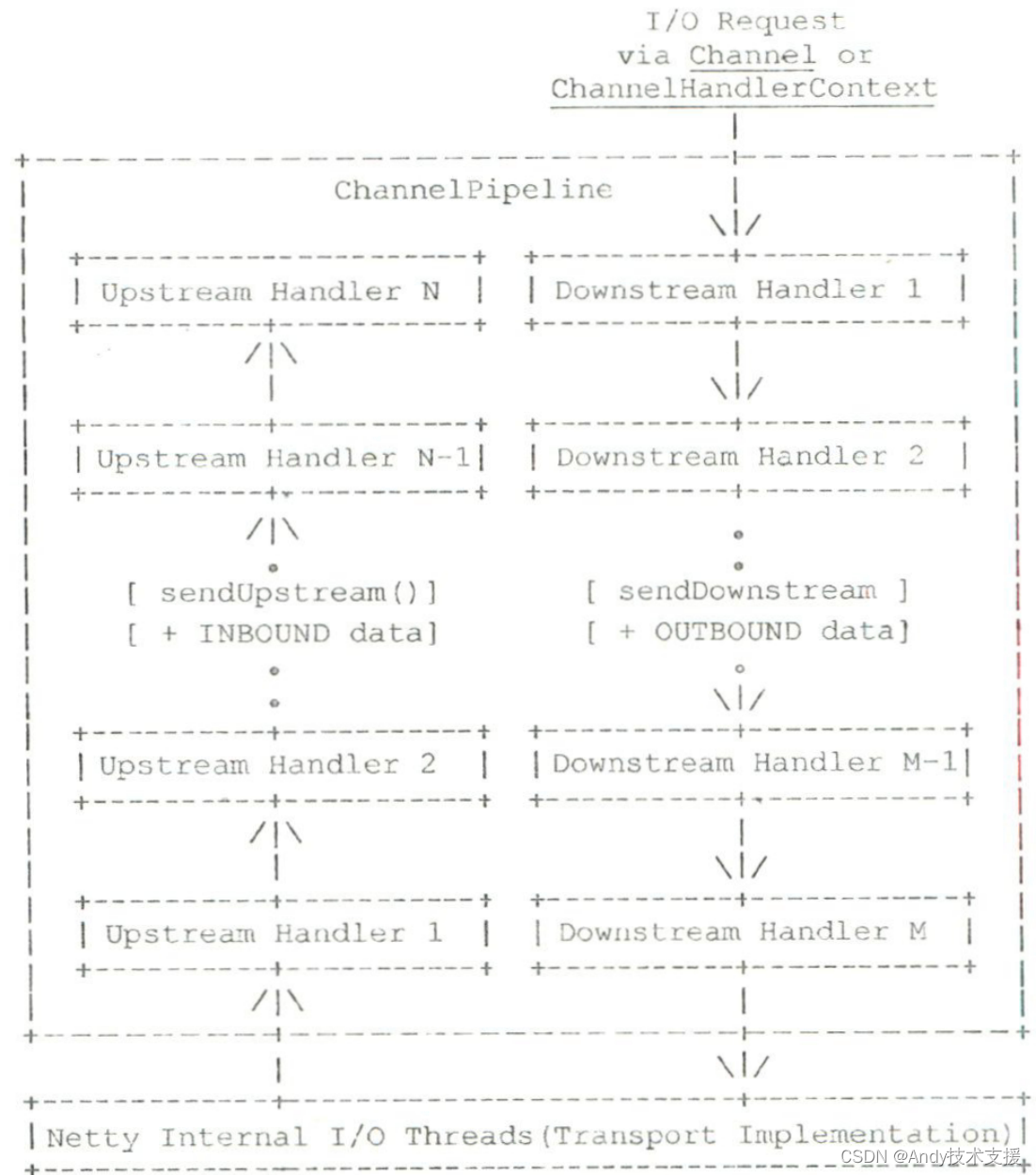
Netty-2-数据编解码
解析编解码支持的原理 以编码为例,要将对象序列化成字节流,你可以使用MessageToByteEncoder或MessageToMessageEncoder类。 这两个类都继承自ChannelOutboundHandlerAdapter适配器类,用于进行数据的转换。 其中,对于MessageToMe…...
伽马校正:FPGA
参考资料: Tone Mapping 与 Gamma Correction - 知乎 (zhihu.com) Book_VIP: 《基于MATLAB与FPGA的图像处理教程》此书是业内第一本基于MATLAB与FPGA的图像处理教程,第一本真正结合理论及算法加速方案,在Matlab验证,以及在FPGA上…...

【SpringCloud笔记】(8)服务网关之GateWay
GateWay 概述简介 官网地址: 上一代网关Zuul 1.x:https://github.com/Netflix/zuul/wiki(有兴趣可以了解一下) gateway:https://cloud.spring.io/spring-cloud-static/spring-cloud-gateway/2.2.1.RELEASE/reference/…...

Compose常用布局
Compose布局基础知识 上一节对Compose做了简单的介绍,本章节主要介绍Compose中常用的布局,其中包括三个基础布局(Colmun、Row、Box);以及其他常用布局(ConstraintLayout 、BoxWithConstraints、HorizontalP…...
使用keytool查看Android APK签名
文章目录 一、找到JDK位置二、使用方法2.1 打开windows命令行工具2.2 查看签名 三、如何给APK做系统签名呢? 一、找到JDK位置 安卓AS之后,可选择继续安装JDK,如本文使用amazon版本默认位置:C:\Users\66176.jdks\corretto-1.8.0_342可通过自…...

数据库学习日常案例20231221-oracle libray cache lock分析
1 问题概述: 阻塞的源头为两个ddl操作导致大量的libray cache lock 其中1133为gis sde的create table as语句。 其中697为alter index语句。...

【数据结构】最短路径算法实现(Dijkstra(迪克斯特拉),FloydWarshall(弗洛伊德) )
文章目录 前言一、Dijkstra(迪克斯特拉)1.方法:2.代码实现 二、FloydWarshall(弗洛伊德)1.方法2.代码实现 完整源码 前言 最短路径问题:从在带权有向图G中的某一顶点出发,找出一条通往另一顶点…...

算法模板之队列图文详解
🌈个人主页:聆风吟 🔥系列专栏:算法模板、数据结构 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 📋前言一. ⛳️模拟队列1.1 🔔用数组模拟实现队列1.1.1 👻队列的定…...
[node]Node.js 中REPL简单介绍
[node]Node.js 中REPL简单介绍 什么是REPL为什么使用REPL如何使用REPL 命令REPL模式node的全局内容展示node全局所有模块查看全局模块具体内容其它命令 实践 什么是REPL Node.js REPL(Read Eval Print Loop:交互式解释器) 表示电脑的环境,类似 Windows 系统的终端或…...
AtomHub 开源容器镜像中心开放公测,国内服务稳定下载
由开放原子开源基金会主导,华为、浪潮、DaoCloud、谐云、青云、飓风引擎以及 OpenSDV 开源联盟、openEuler 社区、OpenCloudOS 社区等成员单位共同发起建设的 AtomHub 可信镜像中心正式开放公测。AtomHub 秉承共建、共治、共享的理念,旨在为开源组织和开…...
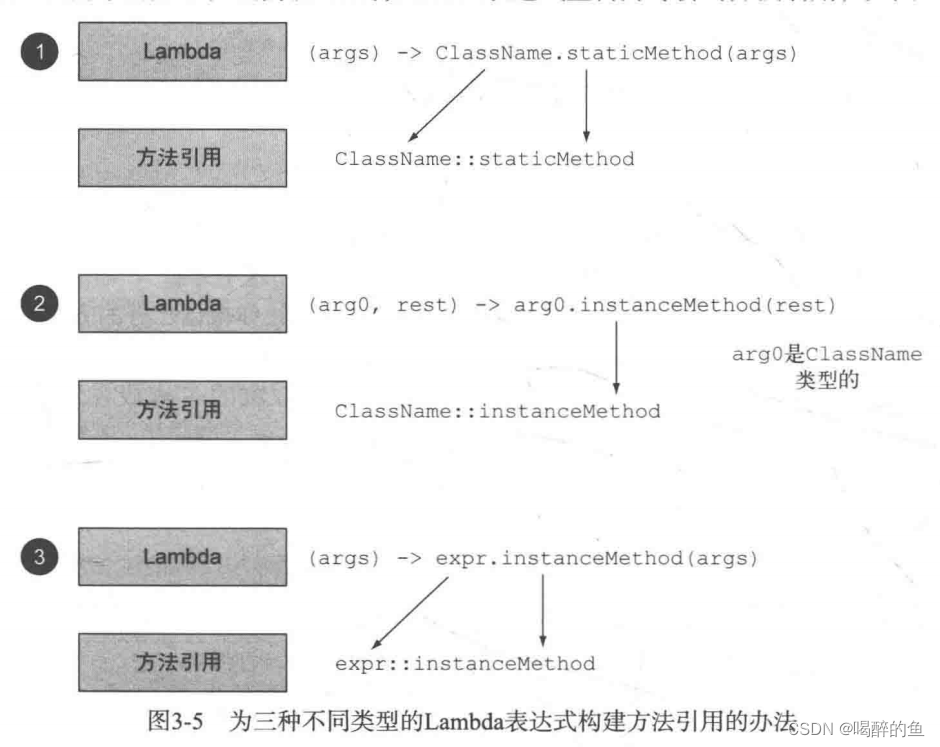
java8实战 lambda表达式、函数式接口、方法引用双冒号(中)
前言 书接上文,上一篇博客讲到了lambda表达式的应用场景,本篇接着将java8实战第三章的总结。建议读者先看第一篇博客 其他函数式接口例子 上一篇有讲到Java API也有其他的函数式接口,书里也举了2个例子,一个是java.util.functi…...

FPGA高端项目:UltraScale GTH + SDI 视频编解码,SDI无缓存回环输出,提供2套工程源码和技术支持
目录 1、前言免责声明 2、相关方案推荐我这里已有的 GT 高速接口解决方案我目前已有的SDI编解码方案 3、详细设计方案设计框图3G-SDI摄像头LMH0384均衡EQUltraScale GTH 的SDI模式应用UltraScale GTH 基本结构参考时钟的选择和分配UltraScale GTH 发送和接收处理流程UltraScale…...

为什么react call api in cDidMount
为什么react call api in cDM 首先,放到constructor或者cWillMount不是语法错误 参考1 参考2 根据上2个参考,总结为: 1、官网就是这么建议的: 2、17版本后的react 由于fiber的出现导致 cWM 会调用多次! cWM 方法已…...

openGauss学习笔记-171 openGauss 数据库运维-备份与恢复-导入数据-深层复制
文章目录 openGauss学习笔记-171 openGauss 数据库运维-备份与恢复-导入数据-深层复制171.1 使用CREATE TABLE执行深层复制171.1.1 操作步骤 171.2 使用CREATE TABLE LIKE执行深层复制171.2.1 操作步骤 171.3 通过创建临时表并截断原始表来执行深层复制171.3.1 操作步骤 openGa…...

[kubernetes]控制平面ETCD
什么是ETCD CoreOS基于Raft开发的分布式key-value存储,可用于服务发现、共享配置以及一致性保障(如数据库选主、分布式锁等)etcd像是专门为集群环境的服务发现和注册而设计,它提供了数据TTL失效、数据改变监视、多值、目录监听、…...

序列化类的高级用法
1.3.3 模型类序列化器 如果我们想要使用序列化器对应的是Django的模型类,DRF为我们提供了ModelSerializer模型类序列化器来帮助我们快速创建一个Serializer类。 ModelSerializer与常规的Serializer相同,但提供了: 基于模型类自动生成一系列…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

STM32 低功耗设计全攻略:PWR 模块原理 + 睡眠 / 停止 / 待机模式实战(串口 + 红外 + RTC 应用全解析)
文章目录 PWRPWR(电源控制模块)核心功能 电源框图上电复位和掉电复位可编程电压监测器低功耗模式模式选择睡眠模式停止模式待机模式 修改主频一、准备工作二、修改主频的核心步骤:宏定义配置三、程序流程:时钟配置函数解析四、注意…...
