【数据结构】最短路径算法实现(Dijkstra(迪克斯特拉),FloydWarshall(弗洛伊德) )
文章目录
- 前言
- 一、Dijkstra(迪克斯特拉)
- 1.方法:
- 2.代码实现
- 二、FloydWarshall(弗洛伊德)
- 1.方法
- 2.代码实现
- 完整源码
前言
最短路径问题:从在带权有向图G中的某一顶点出发,找出一条通往另一顶点的最短路径,最短也就是沿路径各边的权值总和达到最小。
单源最短路径问题:给定一个图G = ( V , E ) G=(V,E)G=(V,E),求源结点s ∈ V s∈Vs∈V到图
中每个结点v ∈ V v∈Vv∈V的最短路径
一、Dijkstra(迪克斯特拉)
1.方法:
针对一个带权有向图G,将所有结点分为两组S和Q,S是已经确定最短路径的结点集合,在初始时
为空(初始时就可以将源节点s放入,毕竟源节点到自己的代价是0),Q 为其余未确定最短路径
的结点集合,每次从Q 中找出一个起点到该结点代价最小的结点u ,将u 从Q 中移出,并放入S
中,对u 的每一个相邻结点v 进行松弛操作。松弛即对每一个相邻结点v ,判断源节点s到结点u
的代价与u 到v 的代价之和是否比原来s 到v 的代价更小,若代价比原来小则要将s 到v 的代价更新
为s 到u 与u 到v 的代价之和,否则维持原样。如此一直循环直至集合Q 为空,即所有节点都已经
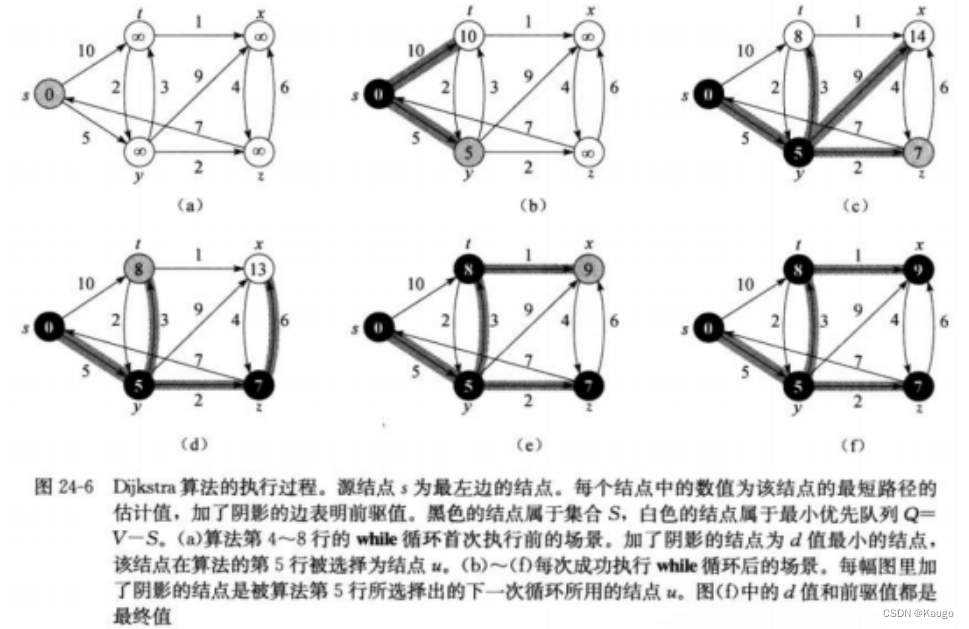
查找过一遍并确定了最短路径, Dijkstra算法每次都是选择V-S中最小的路径节点来进行更新,并加入S中,所以该算法使用的是贪心策略。
核心就是从当前选入的顶点当中去找其直接相连的最小的边,然后用这个最小边相连的另一个顶点为起点,找与其直接相连边中最小的边(eg:与s直接相连的为t,y。最小的边为5,即y顶点,其为s到y的最短距离,然后以y为起点,与y直接相连的有t,x,z。最小的边为2即z点,y到z最短为2,所以s到z最短为7,以此类推,直到所有点都被当过起点后结束)
2.代码实现
void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath){//dist存的src到其他点的最短路径// vector<int> pPath 记录srci-其他顶点最短路径父顶点数组size_t srci = GetVertexIndex(src);size_t n = _vertexs.size();dist.resize(n, MAX_W);pPath.resize(n, -1);dist[srci] = 0;//自己到自己距离为0pPath[srci] = srci;// 已经确定最短路径的顶点集合vector<bool> S(n, false);for (size_t j = 0; j < n; ++j){int u = srci;//u为当前最短路径顶点W min = MAX_W;//min为起始点到u的距离for (size_t i = 0; i < n; ++i){if (S[i] == false && dist[i] < min){u = i;min = dist[i];}}//找到与当前起始点直接相连的最短路径的顶点后//将其位置置为true表明已经选入S[u] = true;// 松弛算法:更新一遍u连接的所有边,看是否能更新出更短连接路径for (size_t v = 0; v < n; ++v){// 如果srci->u + u->k 比 srci->k更短 则进行更新if (S[v] == false && _matrix[u][v] != MAX_W&& dist[u] + _matrix[u][v] < dist[v]){dist[v] = dist[u] + _matrix[u][v];pPath[v] = u;}}}}//打印路径
void PrintShortPath(const V& src, const vector<W>& dist, const vector<int>& pPath) {size_t srci = GetVertexIndex(src);size_t n = _vertexs.size();for (size_t i = 0; i < n; i++) {if (i != srci) {vector<int>path;//path为src到其他顶点路径size_t parenti = i;while (parenti != srci) {path.push_back(parenti);parenti = pPath[parenti];}path.push_back(srci);//需要反转一下,因为我们从s->x->v//是从v的父亲为x再推出x的父亲为s才结束的reverse(path.begin(), path.end());for (auto index : path) {cout << _vertexs[index] << "->";}cout << "权值和:" << dist[i] << endl;}}}
Dijkstra算法存在的问题是不支持图中带负权路径,如果带有负权路径,则可能会找不到一些路
径的最短路径。
二、FloydWarshall(弗洛伊德)
多源最短路径:Floyd-Warshall算法是解决任意两点间的最短路径的一种算法。
1.方法
Floyd算法考虑的是一条最短路径的中间节点,即简单路径p={v1,v2,…,vn}上除v1和vn的任意节
点。
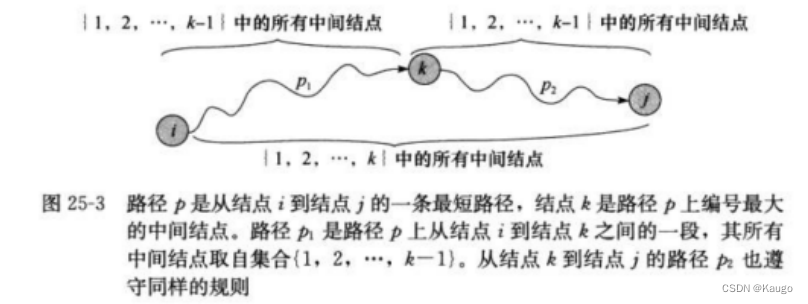
设k是p的一个中间节点,那么从i到j的最短路径p就被分成i到k和k到j的两段最短路径p1,p2。p1
是从i到k且中间节点属于{1,2,…,k-1}取得的一条最短路径。p2是从k到j且中间节点属于{1,
2,…,k-1}取得的一条最短路径。
核心将中间经过的k当成所经过s->…->j中间经过的所有中间顶点集合中的一个,把中间的所有顶点看成k。

2.代码实现
void FloydWarshall(vector<vector<W>>& vvDist, vector<vector<int>>& vvpPath){size_t n = _vertexs.size();vvDist.resize(n);vvpPath.resize(n);// 初始化权值和路径矩阵for (size_t i = 0; i < n; ++i){vvDist[i].resize(n, MAX_W);vvpPath[i].resize(n, -1);}//vvpPath[i][j]表示i->j,j的父亲为i// 直接相连的边更新一下//把目前已知直接相连的边放入vvDist中,并更新vvpPath[i][j]for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){if (_matrix[i][j] != MAX_W){vvDist[i][j] = _matrix[i][j];vvpPath[i][j] = i;}if (i == j){vvDist[i][j] = W();}}}// 最短路径的更新i-> {其他顶点} ->j//这里要进行k次的原因是因为我们所有结点都有可能//成为src与dst的中间结点,所以要考虑所有情况for (size_t k = 0; k < n; ++k){for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){// k 作为的中间点尝试去更新i->j的路径if (vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W&& vvDist[i][k] + vvDist[k][j] < vvDist[i][j]){vvDist[i][j] = vvDist[i][k] + vvDist[k][j];vvpPath[i][j] = vvpPath[k][j];//因为这里k实际上是中间顶点集合// 找跟j相连的上一个邻接顶点// 如果k->j 直接相连,上一个点就k,vvpPath[k][j]存就是k// 如果k->j 没有直接相连,k->...->x->j,vvpPath[k][j]存就是x}}}// 打印权值和路径矩阵观察数据for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){if (vvDist[i][j] == MAX_W){//cout << "*" << " ";printf("%3c", '*');}else{//cout << vvDist[i][j] << " ";printf("%3d", vvDist[i][j]);}}cout << endl;}cout << endl;for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){//cout << vvParentPath[i][j] << " ";printf("%3d", vvpPath[i][j]);}cout << endl;}cout << "=================================" << endl;}}};
完整源码
如果对Graph这些代码不太熟悉的小伙伴可以参考我之前写的【数据结构】图的创建(邻接矩阵,邻接表)以及深度广度遍历(BFS,DFS)
namespace matrix {//V为顶点类型,W为边权值类型,MAX_W为权值最大值也就是无效值//Direction用来判断是不是有向图,false为无向图template<class V,class W,W MAX_W=INT_MAX,bool Direction=false>class Graph {public:Graph() = default;Graph(const V* a, size_t n) {_vertexs.reserve(n);for (size_t i = 0; i < n; i++) {_vertexs.push_back(a[i]);_indexMap[a[i]] = i;//将顶点存入_vertexs,下标映射存进map}_matrix.resize(n);for (size_t i = 0; i < _matrix.size(); i++) {_matrix[i].resize(n, MAX_W);//邻接矩阵默认初始值为无效值}}size_t GetVertexIndex(const V& v) {//获得对应顶点在数组中的下标auto it = _indexMap.find(v);if (it != _indexMap.end()) {return it->second;//有这个顶点返回其下标}else {throw("顶点不存在");return -1;}}void _AddEdge(size_t srci, size_t dsti, const W& w) {//存入权值_matrix[srci][dsti] = w;if (Direction == false) {_matrix[dsti][srci] = w;//无向图要两个方向都存}}void AddEdge(const V& src, const V& dst, const W& w) {//添加边与顶点的关系。从src到dst方向的关系size_t srci = GetVertexIndex(src);size_t dsti = GetVertexIndex(dst);//先获取其对应的下标_AddEdge(srci, dsti, w);}void Print() {for (size_t i = 0; i < _vertexs.size(); i++) {cout << "[" << i << "]" << "->" << _vertexs[i] << endl;}//打印顶点集cout << endl;//打印邻接矩阵for (size_t i = 0; i < _matrix.size(); i++) {cout << i << " ";for (size_t j = 0; j < _matrix[i].size(); j++) {if (_matrix[i][j] == MAX_W) {printf("%4c", '*');}else {printf("%4d", _matrix[i][j]);}}cout << endl;}}void BFS(const V& src) {size_t srci = GetVertexIndex(src);queue<int>q;q.push(srci);vector<bool>visited(_vertexs.size(), false);visited[srci] = true;//标记这个顶点被访问过了int levelSize = 1;while (!q.empty()) {//levelSize为当前层的大小for (size_t i = 0; i < levelSize; i++) {int front = q.front();q.pop();cout << front << ":" << _vertexs[front]<<" ";for (size_t i = 0; i < _vertexs.size(); i++) {if (_matrix[front][i] != MAX_W && visited[i] == false) {q.push(i);visited[i] = true;//标记这个顶点被访问过了}}}levelSize = q.size();//更新当前层的数量cout << endl;}cout << endl;}void _DFS(size_t srci, vector<bool>& visited) {cout << srci << ":" << _vertexs[srci] << endl;visited[srci] = true;//标记这个顶点被访问过了for (size_t i = 0; i < _vertexs.size(); i++) {if (_matrix[srci][i] != MAX_W && visited[i] == false) {_DFS(i, visited);}}}void DFS(const V& src) {size_t srci = GetVertexIndex(src);vector<bool>visited(_vertexs.size(), false);_DFS(srci, visited);}typedef Graph<V, W, MAX_W, false> Self;//建立边的类,保存边的两个顶点下标和权值struct Edge {size_t _srci;size_t _dsti;W _w;Edge(size_t srci,size_t dsti,W w):_srci(srci),_dsti(dsti),_w(w){}bool operator>(const Edge& e)const {return _w > e._w;//小根堆判断}};W Kruskal(Self& minTree){//minTree为最小生成树,刚开始什么都没有size_t n = _vertexs.size();//初始化最小生成树minTree._vertexs = _vertexs;minTree._indexMap = _indexMap;minTree._matrix.resize(n);for (size_t i = 0; i < n; ++i){minTree._matrix[i].resize(n, MAX_W);}//我们每次选边从全部边中选出最小的(保证不构成回路的情况)//所以我们可以考虑用小根堆来存入边,这样每次方便找最小的priority_queue<Edge, vector<Edge>, greater<Edge>> minque;for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){if (i < j && _matrix[i][j] != MAX_W){//将所有有效值边放进堆中minque.push(Edge(i, j, _matrix[i][j]));}}}int size = 0;W totalW = W();UnionFindSet ufs(n); // 选出n-1条边while (!minque.empty()){//取出最小边Edge min = minque.top();minque.pop();if (!ufs.InSet(min._srci, min._dsti))//判断是否成环{//cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] <<":"<<min._w << endl;//不成环就将当前边放入最小生成树当中minTree._AddEdge(min._srci, min._dsti, min._w);//并把这两个顶点放入同一个并查集集合当中ufs.Union(min._srci, min._dsti);++size;totalW += min._w;//权值总和增加}else{//cout << "构成环:";//cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;}}if (size == n - 1)//边数选够说明最小生成树//创建成功{return totalW;}else{return W();}}W Prim(Self& minTree, const W& src){size_t srci = GetVertexIndex(src);size_t n = _vertexs.size();minTree._vertexs = _vertexs;minTree._indexMap = _indexMap;minTree._matrix.resize(n);for (size_t i = 0; i < n; ++i){minTree._matrix[i].resize(n, MAX_W);}vector<bool> X(n, false);vector<bool> Y(n, true);X[srci] = true;Y[srci] = false;// 从X->Y集合中连接的边里面选出最小的边priority_queue<Edge, vector<Edge>, greater<Edge>> minq;// 先把srci连接的边添加到小根堆中for (size_t i = 0; i < n; ++i){if (_matrix[srci][i] != MAX_W){minq.push(Edge(srci, i, _matrix[srci][i]));}}cout << "Prim开始选边" << endl;size_t size = 0;//选出边的数量W totalW = W();//权值之和while (!minq.empty()){Edge min = minq.top();minq.pop();// 最小边的目标点也在X集合,则构成环if (X[min._dsti]){//cout << "构成环:";//cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;}else{//从Y中选出顶点minTree._AddEdge(min._srci, min._dsti, min._w);//加入最小生成树//cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;X[min._dsti] = true;Y[min._dsti] = false;++size;totalW += min._w;if (size == n - 1)break;//把新加入顶点相关的边都放入小根堆中for (size_t i = 0; i < n; ++i){if (_matrix[min._dsti][i] != MAX_W && Y[i]){minq.push(Edge(min._dsti, i, _matrix[min._dsti][i]));}}}}if (size == n - 1){return totalW;}else{return W();}}void PrintShortPath(const V& src, const vector<W>& dist, const vector<int>& pPath) {size_t srci = GetVertexIndex(src);size_t n = _vertexs.size();for (size_t i = 0; i < n; i++) {if (i != srci) {vector<int>path;//path为src到其他顶点路径size_t parenti = i;while (parenti != srci) {path.push_back(parenti);parenti = pPath[parenti];}path.push_back(srci);//需要反转一下,因为我们从s->x->v//是从v的父亲为x再推出x的父亲为s才结束的reverse(path.begin(), path.end());for (auto index : path) {cout << _vertexs[index] << "->";}cout << "权值和:" << dist[i] << endl;}}}void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath){//dist存的src到其他点的最短路径// vector<int> pPath 记录srci-其他顶点最短路径父顶点数组size_t srci = GetVertexIndex(src);size_t n = _vertexs.size();dist.resize(n, MAX_W);pPath.resize(n, -1);dist[srci] = 0;//自己到自己距离为0pPath[srci] = srci;// 已经确定最短路径的顶点集合vector<bool> S(n, false);for (size_t j = 0; j < n; ++j){int u = srci;//u为当前最短路径顶点W min = MAX_W;//min为起始点到u的距离for (size_t i = 0; i < n; ++i){if (S[i] == false && dist[i] < min){u = i;min = dist[i];}}//找到与当前起始点直接相连的最短路径的顶点后//将其位置置为true表明已经选入S[u] = true;// 松弛算法:更新一遍u连接的所有边,看是否能更新出更短连接路径for (size_t v = 0; v < n; ++v){// 如果srci->u + u->k 比 srci->k更短 则进行更新if (S[v] == false && _matrix[u][v] != MAX_W&& dist[u] + _matrix[u][v] < dist[v]){dist[v] = dist[u] + _matrix[u][v];pPath[v] = u;}}}}void FloydWarshall(vector<vector<W>>& vvDist, vector<vector<int>>& vvpPath){size_t n = _vertexs.size();vvDist.resize(n);vvpPath.resize(n);// 初始化权值和路径矩阵for (size_t i = 0; i < n; ++i){vvDist[i].resize(n, MAX_W);vvpPath[i].resize(n, -1);}//vvpPath[i][j]表示i->j,j的父亲为i// 直接相连的边更新一下//把目前已知直接相连的边放入vvDist中,并更新vvpPath[i][j]for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){if (_matrix[i][j] != MAX_W){vvDist[i][j] = _matrix[i][j];vvpPath[i][j] = i;}if (i == j){vvDist[i][j] = W();}}}// 最短路径的更新i-> {其他顶点} ->j//这里要进行k次的原因是因为我们所有结点都有可能//成为src与dst的中间结点,所以要考虑所有情况for (size_t k = 0; k < n; ++k){for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){// k 作为的中间点尝试去更新i->j的路径if (vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W&& vvDist[i][k] + vvDist[k][j] < vvDist[i][j]){vvDist[i][j] = vvDist[i][k] + vvDist[k][j];vvpPath[i][j] = vvpPath[k][j];//因为这里k实际上是中间顶点集合// 找跟j相连的上一个邻接顶点// 如果k->j 直接相连,上一个点就k,vvpPath[k][j]存就是k// 如果k->j 没有直接相连,k->...->x->j,vvpPath[k][j]存就是x}}}// 打印权值和路径矩阵观察数据for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){if (vvDist[i][j] == MAX_W){//cout << "*" << " ";printf("%3c", '*');}else{//cout << vvDist[i][j] << " ";printf("%3d", vvDist[i][j]);}}cout << endl;}cout << endl;for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){//cout << vvParentPath[i][j] << " ";printf("%3d", vvpPath[i][j]);}cout << endl;}cout << "=================================" << endl;}}private:vector<V>_vertexs;//顶点集合map<V, int>_indexMap;//存顶点与数组下标的映射关系vector<vector<W>>_matrix;//邻接矩阵};}
相关文章:

【数据结构】最短路径算法实现(Dijkstra(迪克斯特拉),FloydWarshall(弗洛伊德) )
文章目录 前言一、Dijkstra(迪克斯特拉)1.方法:2.代码实现 二、FloydWarshall(弗洛伊德)1.方法2.代码实现 完整源码 前言 最短路径问题:从在带权有向图G中的某一顶点出发,找出一条通往另一顶点…...

算法模板之队列图文详解
🌈个人主页:聆风吟 🔥系列专栏:算法模板、数据结构 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 📋前言一. ⛳️模拟队列1.1 🔔用数组模拟实现队列1.1.1 👻队列的定…...
[node]Node.js 中REPL简单介绍
[node]Node.js 中REPL简单介绍 什么是REPL为什么使用REPL如何使用REPL 命令REPL模式node的全局内容展示node全局所有模块查看全局模块具体内容其它命令 实践 什么是REPL Node.js REPL(Read Eval Print Loop:交互式解释器) 表示电脑的环境,类似 Windows 系统的终端或…...
AtomHub 开源容器镜像中心开放公测,国内服务稳定下载
由开放原子开源基金会主导,华为、浪潮、DaoCloud、谐云、青云、飓风引擎以及 OpenSDV 开源联盟、openEuler 社区、OpenCloudOS 社区等成员单位共同发起建设的 AtomHub 可信镜像中心正式开放公测。AtomHub 秉承共建、共治、共享的理念,旨在为开源组织和开…...
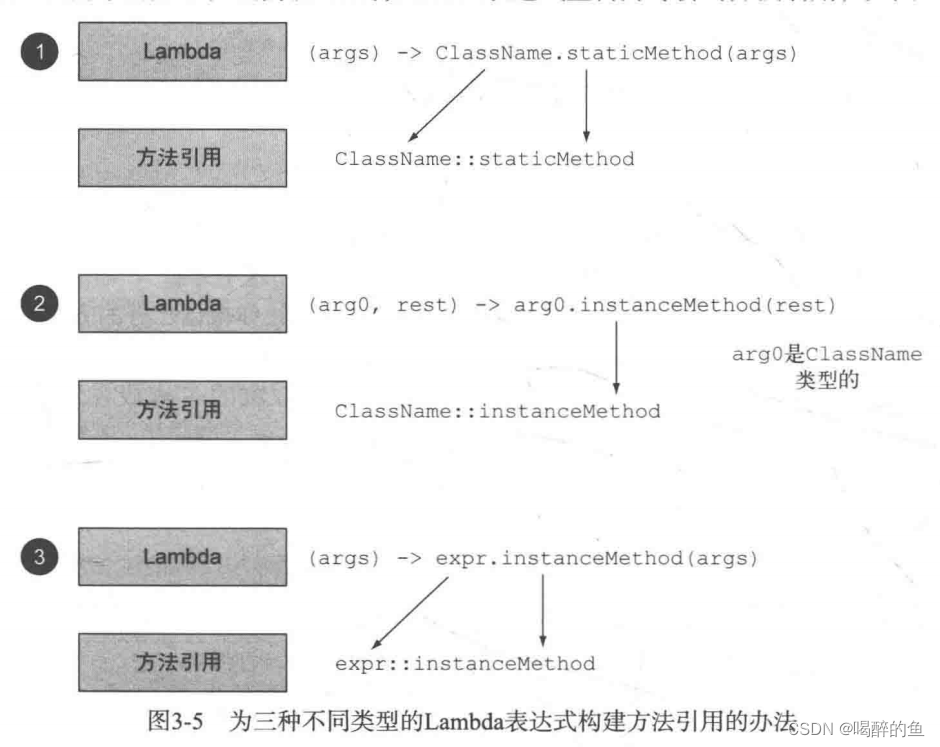
java8实战 lambda表达式、函数式接口、方法引用双冒号(中)
前言 书接上文,上一篇博客讲到了lambda表达式的应用场景,本篇接着将java8实战第三章的总结。建议读者先看第一篇博客 其他函数式接口例子 上一篇有讲到Java API也有其他的函数式接口,书里也举了2个例子,一个是java.util.functi…...

FPGA高端项目:UltraScale GTH + SDI 视频编解码,SDI无缓存回环输出,提供2套工程源码和技术支持
目录 1、前言免责声明 2、相关方案推荐我这里已有的 GT 高速接口解决方案我目前已有的SDI编解码方案 3、详细设计方案设计框图3G-SDI摄像头LMH0384均衡EQUltraScale GTH 的SDI模式应用UltraScale GTH 基本结构参考时钟的选择和分配UltraScale GTH 发送和接收处理流程UltraScale…...

为什么react call api in cDidMount
为什么react call api in cDM 首先,放到constructor或者cWillMount不是语法错误 参考1 参考2 根据上2个参考,总结为: 1、官网就是这么建议的: 2、17版本后的react 由于fiber的出现导致 cWM 会调用多次! cWM 方法已…...

openGauss学习笔记-171 openGauss 数据库运维-备份与恢复-导入数据-深层复制
文章目录 openGauss学习笔记-171 openGauss 数据库运维-备份与恢复-导入数据-深层复制171.1 使用CREATE TABLE执行深层复制171.1.1 操作步骤 171.2 使用CREATE TABLE LIKE执行深层复制171.2.1 操作步骤 171.3 通过创建临时表并截断原始表来执行深层复制171.3.1 操作步骤 openGa…...

[kubernetes]控制平面ETCD
什么是ETCD CoreOS基于Raft开发的分布式key-value存储,可用于服务发现、共享配置以及一致性保障(如数据库选主、分布式锁等)etcd像是专门为集群环境的服务发现和注册而设计,它提供了数据TTL失效、数据改变监视、多值、目录监听、…...

序列化类的高级用法
1.3.3 模型类序列化器 如果我们想要使用序列化器对应的是Django的模型类,DRF为我们提供了ModelSerializer模型类序列化器来帮助我们快速创建一个Serializer类。 ModelSerializer与常规的Serializer相同,但提供了: 基于模型类自动生成一系列…...
4.svn版本管理工具使用
1. 什么是SVN 版本控制 它可以记录每一次文件和目录的修改情况,这样就可以借此将数据恢复到以前的版本,并可以查看数据的更改细节! Subversion(简称SVN)是一个自由开源的版本控制系统。在Subversion管理下,文件和目录可以超越时空 SVN的优势 统一的版本号 Subversi…...

ZKP Algorithms for Efficient Cryptographic Operations 1 (MSM Pippenger)
MIT IAP 2023 Modern Zero Knowledge Cryptography课程笔记 Lecture 6: Algorithms for Efficient Cryptographic Operations (Jason Morton) Multi-scalar Multiplication(MSM) Naive: nP (((P P) P) P)… (2(2P))…Binary expand $n e_0e_1\alphae_2\alpha2\dots\e_{\…...
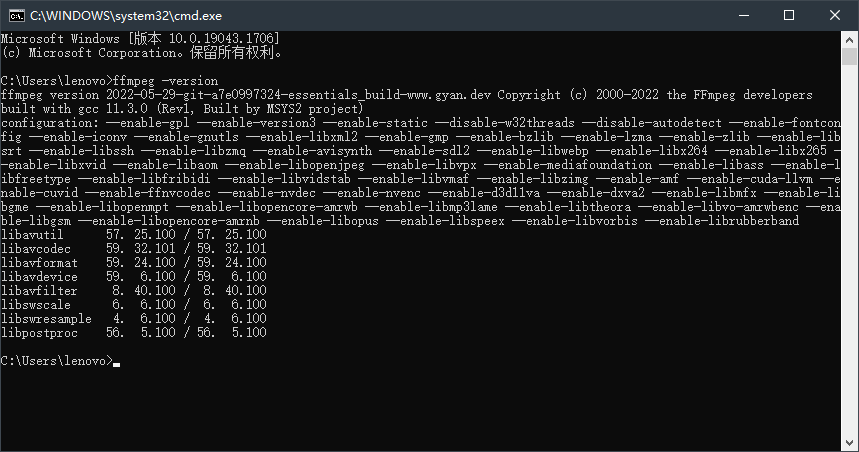
Windows系统安装 ffmpeg
下载及解压 ffmpeg官方下载地址:https://ffmpeg.org/download.html 下载好后将其解压至你想保存的位置中。 环境变量设置 打开Windows设置,在搜索框输入:系统高级设置。 新建环境变量,并输入bin目录具体位置。 安装检查 按住 w…...
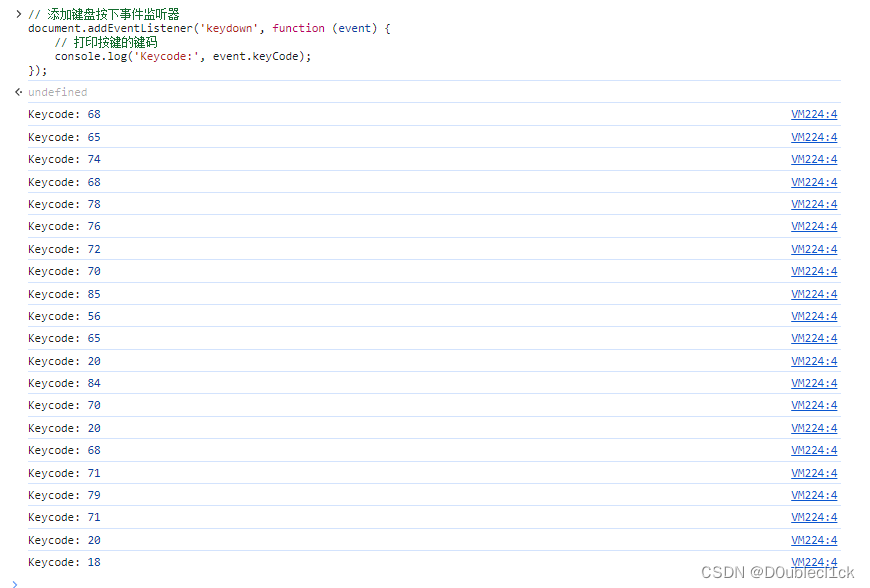
油猴脚本教程案例【键盘监听】-编写 ChatGPT 快捷键优化
文章目录 1. 元数据namenamespaceversiondescriptionauthormatchgranticon 2. 编写函数.1 函数功能2.1.1. input - 聚焦发言框2.1.2. stop - 取消回答2.1.3. newFunction - 开启新窗口2.1.4. scroll - 回到底部 3. 监听键盘事件3.1 监听X - 开启新对话3.2 监听Z - 取消回答3.3 …...

数据结构 | 查漏补缺
目录 数据的基本单位 冒泡排序 DFS和BFS中文 Prim 比较 中序线索二叉树 顺序栈 链栈 时间复杂度 循环队列 求第K个结点的值 数据的基本单位 数据元素 循环队列sq中,用数组elem[0‥25]存放数据元素,设当前sq->front为20,sq-&g…...

回溯算法练习题
78. 子集 中等 1.9K 相关企业 给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。 解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。 示例 1: 输入:nums [1,2,3] 输出&#x…...

代码随想录算法训练营 | day60 单调栈 84.柱状图中最大的矩形
刷题 84.柱状图中最大的矩形 题目链接 | 文章讲解 | 视频讲解 题目:给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。 求在该柱状图中,能够勾勒出来的矩形的最大面积。 1 < heights.len…...
vscode中vue项目报错
当在vscode中写代码时,报错报错报错......... 已经头大,还没写就报错, 这是因为eslint对语法的要求太过严格导致的编译时,出现各种语法格式错误 我们打开vue.config.js,加上这句代码,就OK啦 lintOnSave:…...
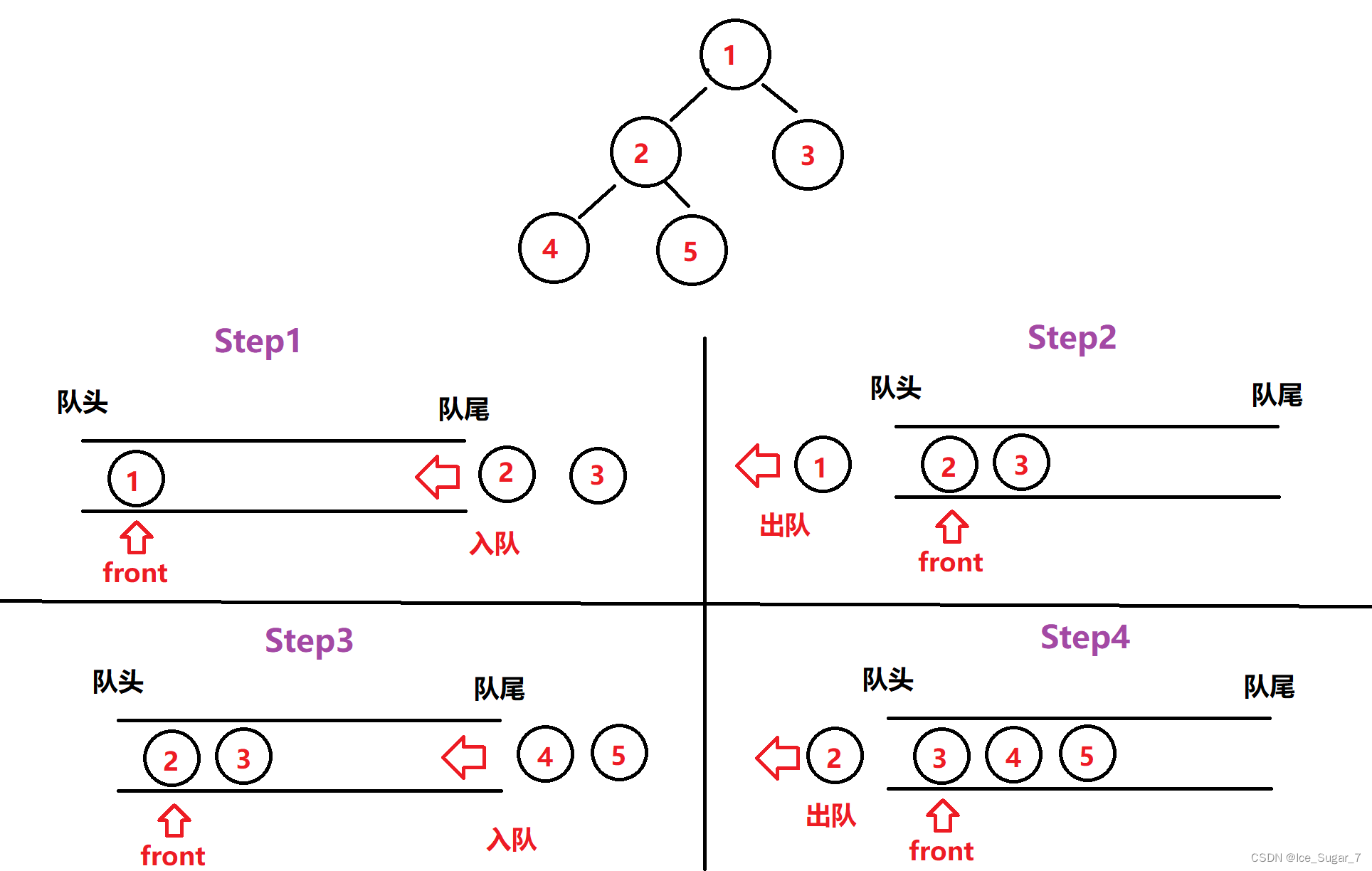
「数据结构」二叉树2
🎇个人主页:Ice_Sugar_7 🎇所属专栏:初阶数据结构 🎇欢迎点赞收藏加关注哦! 文章目录 🍉前言🍉链式结构🍉遍历二叉树🍌前序遍历🍌中序遍历&#x…...

数据处理系列课程 01:谈谈数据处理在数据分析中的重要性
一、数据分析 可能很多朋友第一次听到这个名词,那么我们先来谈一谈什么是数据分析。 数据分析是指用适当的统计分析方法对收集来的大量数据进行分析,将它们加以汇总和理解,以求最大化地开发数据的功能,发挥数据的作用。数据分析是…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...
