OD 完美走位
题目描述:
在第一人称射击游戏中,玩家通过键盘的A、S、D、W四个按键控制游戏人物分别向左、向后、向右、向前进行移动,从而完成走位。假设玩家每按动一次键盘,游戏人物会向某个方向移动一步,如果玩家在操作一定次数的键盘并且各个方向的步数相同时,此时游戏人物必定会回到原点,则称此次走位为完美走位。
现给定玩家的走位(例如:ASDA),请通过更换其中一段连续走位的方式使得原走位能够变成一个完美走位。其中待更换的连续走位可以是相同长度的任何走位。
请返回待更换的连续走位的最小可能长度。
若果原走位本身是一个完美走位,则返回0。
输入描述:
输入为由键盘字母表示的走位s,例如:ASDA
输出描述:
输出为待更换的连续走位的最小可能长度
补充说明:
1、走位长度1 <= s.length <= 10^5
2、s.length 是 4 的倍数
3、s 中只含有 'A', 'S', 'D', 'W' 四种字符
收起
示例1
输入:
ASDW
输出:
0
说明:
已经是完美走位了
示例2
输入:
AASW
输出:
1
说明:
需要把一个A更换成D,这样可以得到“ADSW”或者“DASW”
示例3
输入:
AAAA
输出:
3
说明:
可以替换后 3 个 'A',得到ASDW。
public class 完美走位 {static int minT = 1000000;static String walk;static int w, s, a, d, avg;public static void main(String[] args) {
// walk = "AAAA";Scanner scanner = new Scanner(System.in);walk = scanner.nextLine().toUpperCase();avg = walk.length() / 4;w = Math.max(walk.replaceAll("[^W]", "").length() - avg, 0);s = Math.max(walk.replaceAll("[^S]", "").length() - avg, 0);a = Math.max(walk.replaceAll("[^A]", "").length() - avg, 0);d = Math.max(walk.replaceAll("[^D]", "").length() - avg, 0);solveP();}static void solveP() {if (w == s && s == a && a == d) { // 完美情况System.out.println(0);return;}System.out.println(containstr(0, w + s + a + d - 1, minT));}static int containstr(int head, int tail, int minT) {if (tail > walk.length()) {return minT; // 越界即结束}if (countOccurrences(walk.substring(head, tail), 'W') >= w&& countOccurrences(walk.substring(head, tail), 'S') >= s&& countOccurrences(walk.substring(head, tail), 'A') >= a&& countOccurrences(walk.substring(head, tail), 'D') >= d) { // 我们只需要考虑多余的wasd数量即可minT = Math.min(minT, tail - head); // 更新minTreturn containstr(head + 1, tail, minT); // 右边框右滑} else {return containstr(head, tail + 1, minT); // 左边框右滑}}static int countOccurrences(String str, char ch) {int length = str.replaceAll("[^" + ch + "]", "").length();return length;}}相关文章:

OD 完美走位
题目描述: 在第一人称射击游戏中,玩家通过键盘的A、S、D、W四个按键控制游戏人物分别向左、向后、向右、向前进行移动,从而完成走位。假设玩家每按动一次键盘,游戏人物会向某个方向移动一步,如果玩家在操作一定次数的键…...

SpringSecurity6 | 失败后的跳转
✅作者简介:大家好,我是Leo,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉 🍎个人主页:Leo的博客 💞当前专栏: Java从入门到精通 ✨特色专栏: MySQL学习 🥭本文内容: SpringSecurity6 | 失败后的跳转 📚个人知识库: Leo知识库,欢迎大家访问 学习…...
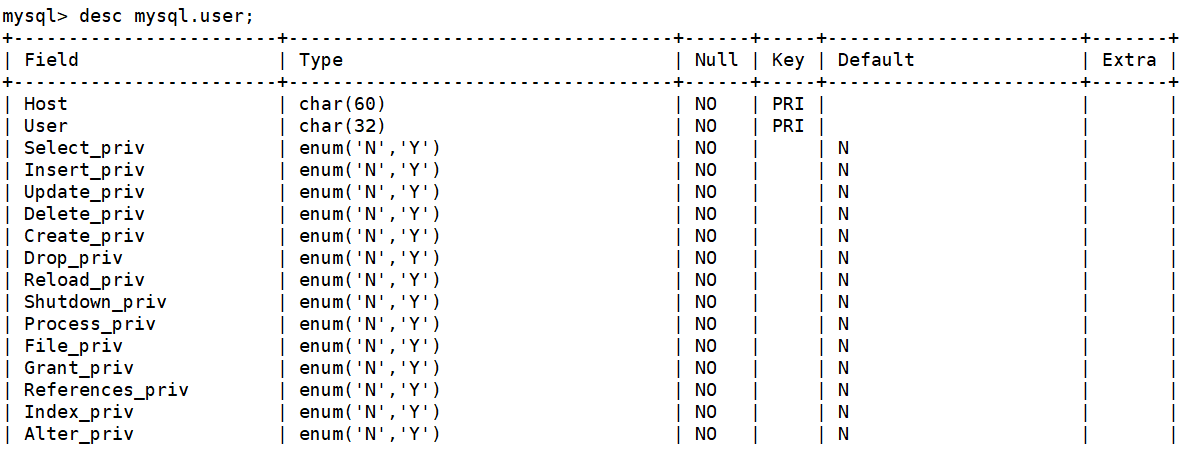
MySQL数据库增删改查
常用的数据类型: int:整数类型,无符号的范围【0,2^32-1】,有符号【-2^31,2^31-1】 float:单精度浮点,4字节64位 double:双精度浮点,8字节64位 char:固定长…...
Altium Designer(AD24)新工程复用设计文件图文教程及视频演示
🏡《专栏目录》 目录 1,概述2,复用方法一视频演示2.1,创建工程2.2,复用设计文件 3,复用方法二视频演示4,总结 欢迎点击浏览更多高清视频演示 1,概述 本文简述使用AD软件复用设计文件…...

Python遥感影像深度学习指南(1)-使用卷积神经网络(CNN、U-Net)和 FastAI进行简单云层检测
【遥感影像深度学习】系列的第一章,Python遥感影像深度学习的入门课程,介绍如何使用卷积神经网络(CNN)从卫星图像中分割云层 1、数据集 在本项目中,我们将使用 Kaggle 提供的 38-Cloud Segmentation in Satellite Images数据集。 该数据集由裁剪成 384x384 (适用…...
)
Hive-DML详解(超详细)
文章目录 前言HiveQL的数据操作语言(DML)1. 插入数据1.1 直接插入固定值1.2 插入查询结果 2. 更新数据3. 删除数据3.1 删除整个分区 4. 查询数据4.1 基本查询4.2 条件筛选4.3 聚合函数 总结 前言 本文将介绍HiveQL的数据操作语言(DML&#x…...

PHP实现可示化代码
PHP是一种服务器端脚本语言,它主要用于开发Web应用程序。虽然PHP本身不提供可视化代码的功能,但你可以使用一些第三方库和工具来实现可视化代码。 以下是一些常用的PHP可视化代码的工具和库: 1. Graphviz:Graphviz是一个开源的可…...

useState语法讲解
useState语法讲解 语法定义 const [state, dispatch] useState(initData)state:定义的数据源,可视作一个函数组件内部的变量,但只在首次渲染被创造。dispatch:改变state的函数,推动函数渲染的渲染函数。dispatch有两…...
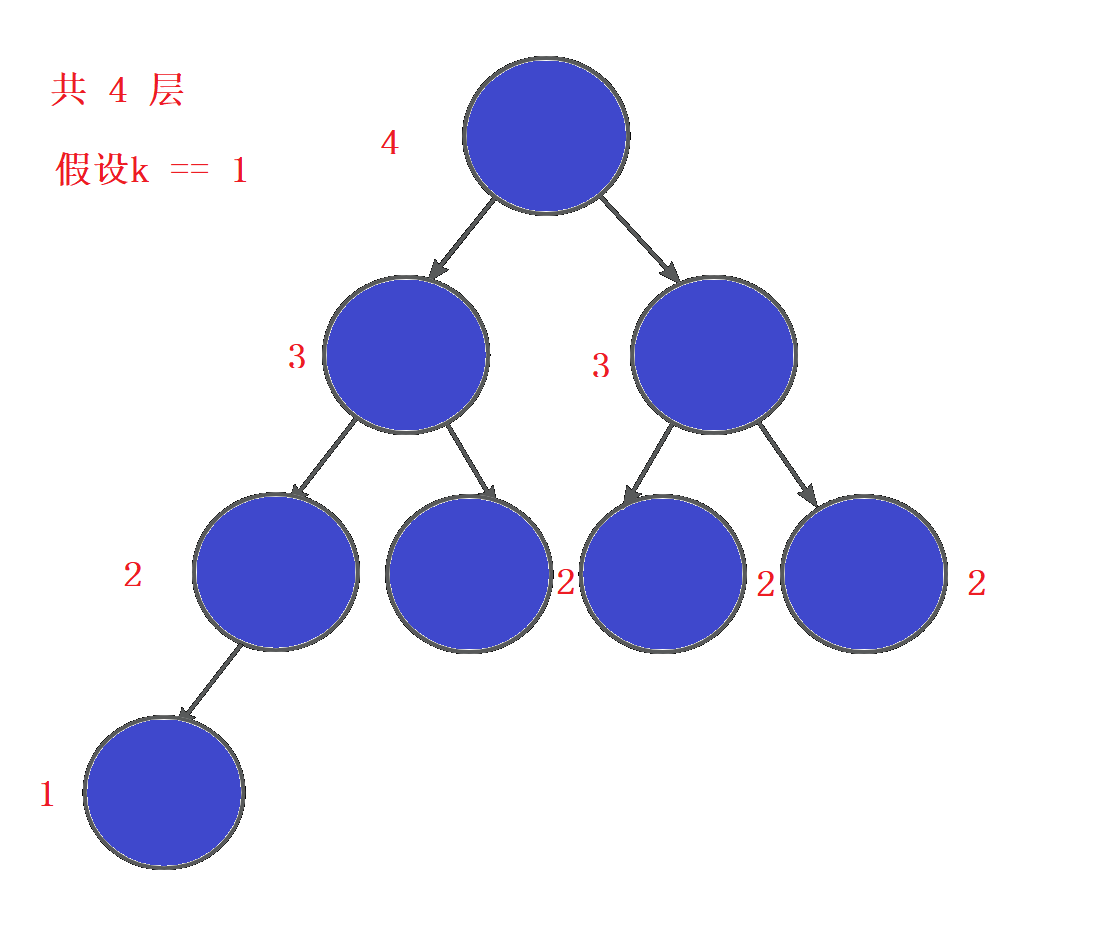
堆与二叉树(下)
接着上次的,这里主要介绍的是堆排序,二叉树的遍历,以及之前讲题时答应过的简单二叉树问题求解 堆排序 给一组数据,升序(降序)排列 思路 思考:如果排列升序,我们应该建什么堆&#x…...

讲诉JVM
jvm是Java代码运行的环境,他将java程序翻译成为机器可以可以识别的机器码,可以跨平台运行如linuc或者windos 简单说一下我对jvm运行的理解, 首先我们运行程序的时候,类加载器会将类按需加载到元空间/方法区里面 …...

8、SpringCloud高频面试题-版本1
1、SpringCloud组件有哪些 SpringCloud 是一系列框架的有序集合。它利用 SpringBoot 的开发便利性巧妙地简化了分布式系统基础设施的开发,如服务发现注册、配置中心、消息总线、负载均衡、断路器、数据监控等,都可以用 SpringBoot 的开发风格做到一键启…...
PHP案例代码:PHP如何提供下载功能?
对Web开发人员来说,“下载”功能是一个非常常见的需求。在网站中提供文件下载,通常用于提供用户手册、软件升级、音乐、视频等各种资源文件。本教程将向您介绍如何实现一个PHP下载功能,同时告诉浏览器文件名称、文件大小、文件类型,并统计下载次数。 首先,我们需要了解一些…...
The Cherno C++笔记 03
目录 Part 07 How the C Linker Works 1.链接 2.编译链接过程中出现的错误 2.1 缺少入口函数 注意:如何区分编译错误还是链接错误 注意:入口点可以自己设置 2.2 找不到自定义函数 2.2.1缺少声明 2.2.2自定义函数与引用函数不一致 2.3 在头文件中放入定义 …...

蓝牙物联网与嵌入式开发如何结合?
蓝牙物联网与嵌入式开发可以紧密结合,以实现更高效、更智能的物联网应用。以下是一些结合的方式: 嵌入式开发为蓝牙设备提供硬件基础设施和控制逻辑:嵌入式系统可以利用微处理器和各种外设组成的系统,为蓝牙设备提供硬件基础设施和…...
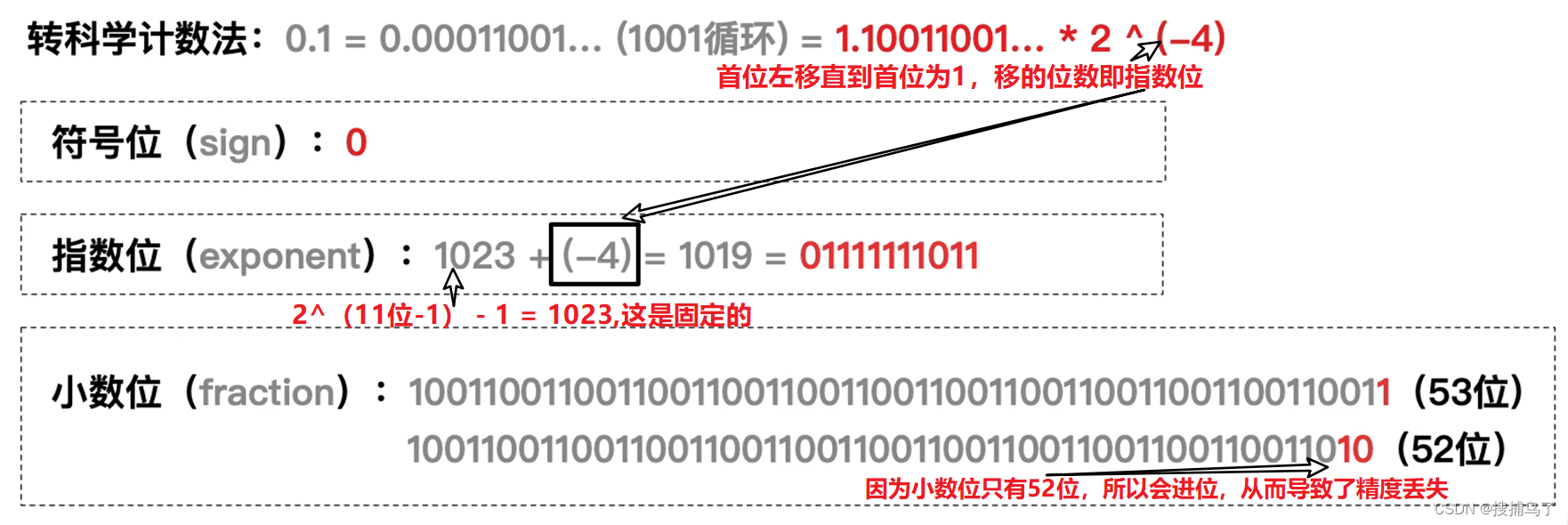
前端面试——JavaScript面经(持续更新)
一、数据类型 1. JavaScript用哪些数据类型、它们有什么区别? JavaScript共有八种数据类型,分别包括5种基本数据类型和3种非基本数据类型。 基本数据类型:Undefined、Null、Boolean、Number、String。非基本数据类型:Object、S…...
微前端——无界wujie
B站课程视频 课程视频 课程课件笔记: 1.微前端 2.无界 现有的微前端框架:iframe、qiankun、Micro-app(京东)、EMP(百度)、无届 前置 初始化 新建一个文件夹 1.通过npm i typescript -g安装ts 2.然后可…...

连锁便利店管理系统有什么用
连锁便利店管理系统对于连锁便利店的运营和管理非常有用。以下是一些常见的用途: 1. 库存管理:连锁便利店通常需要管理多个门店的库存,管理系统可以帮助实时掌握各个门店的库存情况,包括商品数量、进货记录、库存调拨等。这样可以…...
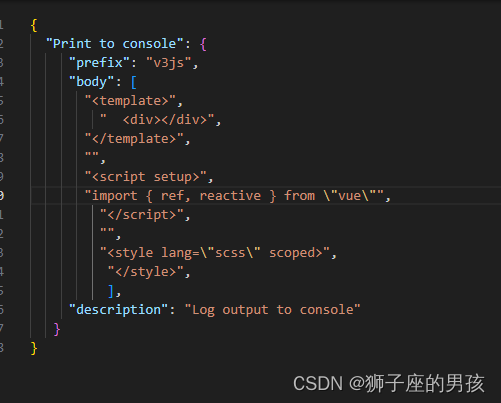
Vue 的两种实现:VSCode 中配置 vue 模板快捷方式的过程
1、创建配置文件: 其一、打开 VSCode ,CtrlShiftP, 打开搜索框: 其二、输入:user, 并点击进去 Snippets:Configure User Snippets 其三、输入 vue3js 并回车: 其四、打开项目,发现配置文件 vue3js.code-sn…...

electron 切换至esm
前言 好消息,经过不知道多少年的讨论。 electron28.0.0开始(23.08.31),默认支持esm了。 see https://github.com/electron/electron/issues/21457 使用方法 升级至electron^28.0.0简单地在package.json中添加"type":…...

【新版】软考 - 系统架构设计师(总结笔记)
个人总结学习笔记,仅供参考!!!! →点击 笔者主页,欢迎关注哦(互相学习,共同成长) 笔记目录 📢【系统架构设计系列】系统架构设计专业技能 计算机组成与结构操作系统信…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...
