D3839|完全背包
完全背包:
首先01背包的滚动数组中的解法是内嵌的循环是从大到小遍历,为了保证每个物品仅被添加一次。
for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}而完全背包的物品是可以添加多次的,所以要从小到大去遍历,即:
// 先遍历物品,再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}同时找到规律,如果存在后序遍历(比如01背包的滚动数组)的话,两个for循环的顺序就不可以变,但如果都是正序的话,两个for循环的顺序就可以进行改变。
518.零钱兑换||
题解复盘:
1)dp数组的含义:dp[j]:凑成总金额j的货币组合数为dp[j]
2)数组的递推公式:dp[j] += dp[j - coins[i]];
3)初始化:
dp[0] = 1 ;
下标非0的dp[j]初始化为0,dp[0]=1还说明了一种情况:如果正好选了coins[i]后,也就是j-coins[i] == 0的情况表示这个硬币刚好能选,此时dp[0]为1表示只选coins[i]存在这样的一种选法。
4)确定遍历顺序:
所以纯完全背包是能凑成总和就行,不用管怎么凑的。
本题是求凑出来的方案个数,且每个方案个数是为组合数。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品
5)举例推导dp数组

大概的数字变化情况,coins[1]的dp[2] = coins[0]那排的dp[2] + coins[1]的dp[0],不选coins[1]的方法数加上选coins[1]的方法数.
class Solution {public int change(int amount, int[] coins) {int[] dp = new int[amount+1];dp[0] = 1;for(int i = 0;i<coins.length;i++){for(int j=coins[i];j<amount+1;j++ ){if(j-coins[i]<0){dp[j] = dp[j];}else{dp[j] = dp[j]+dp[j-coins[i]];}}}return dp[amount];}
}377.组合总和IV
这道题相较于上一道感觉是由求组合数变为了求排列数。
class Solution {public int combinationSum4(int[] nums, int target) {int[] dp = new int[target+1];Arrays.sort(nums);if(nums[0]<target){dp[0] = 1;}else{dp[0] = 0;}for(int i = nums[0];i<target+1;i++){for(int j = 0;j<nums.length;j++){if(i-nums[j]>=0){dp[i] = dp[i]+dp[i-nums[j]];}else{dp[i] = dp[i];}}}return dp[target];}
}70. 爬楼梯(进阶版)
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬至多m (1 <= m < n)个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数
初始思路:
之前的爬楼梯每次爬1,2个台阶,dp(3) = dp(1)+dp(2)
由此推断每次爬1 <= m,dp(m+1) = dp(m)+dp(m-1)+...+dp(1)
分析动态规划五部曲:
(1)dp数组的含义:dp[j] 爬j阶台阶的方法数。
(2)dp的递推公式:
dp[n] = dp[n-m]+dp[n-m+1]+...+dp[n-1];
(3) 初始化:
dp[1] = 1;
dp[2] = 2;
dp[3] = dp[2]+dp[1]+1;
dp[4] = dp[3]+dp[2]+dp[1]+1;
dp[0] = 1;
dp[1] = dp[1]+dp[0];
dp[2] = dp[2]+dp[1]+dp[0];
(4)循环方式,先背包容量再物品,这样每一个容量都可以遍历一次所需要的物品
(5)举例:
import java.util.Arrays;
import java.util.Scanner;public class Main {public static int climbStairs(int n, int m) {int[] dp = new int[n + 1];Arrays.fill(dp, 0);dp[0] = 1;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {if (i - j >= 0) {dp[i] += dp[i - j];}}}return dp[n];}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();System.out.println(climbStairs(n, m));}
}可以理解题解,但是卡码网会超时不知道为什么。
322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
初始思路&&题解复盘:
感觉是在完全背包的基础上变为了最少的硬币个数。之前是由小数开始遍历,如果要是最少的硬币个数感觉从大数开始遍历比较好?
动态规划五部曲:
1.dp数组的定义
dp[j]组成j元所需要的最少硬币数
2.递归数组
dp[j] = Math.min(dp[j],dp[j-coins[i]]+1)
3.初始化(这里没想到)
dp[0] = 0;
dp[i] = MAX_VALUE;
4.遍历顺序
考虑到组合问题,所以先循环物品,再循环背包
只有dp[j-coins[i]]不是初始最大值时,该位才有选择的必要
//只有dp[j-coins[i]]不是初始最大值时,该位才有选择的必要if (dp[j - coins[i]] != max) {//选择硬币数目最小的情况dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);}5.推导
所以这道题目非常关键的地方一个是注意初始化,一个是只有满足条件时,该位的数值才发生更新。
279.完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
初始思路:
由题意可知,这道题需要我们自己构建coins数组,如果这个数小于16,那么我们的数组就只需要装1,4,9,剩下的步骤同上一题一样,注意处理一些较少数目的特殊情况。
class Solution {public int numSquares(int amount) {if(amount<4){return amount;}int n = 0;for(int i = 0;i<amount;i++){if(i*i>amount){n=i-1;break;}}int[] coins = new int[n];for(int i = 0;i<coins.length;i++){coins[i] = (i+1)*(i+1);}int[] dp = new int[amount+1];dp[0] = 0;for(int i = 1;i<amount+1;i++){dp[i] = Integer.MAX_VALUE;}for(int i = 0;i<coins.length;i++){for(int j = coins[i];j<amount+1;j++){dp[j] = Math.min(dp[j],dp[j-coins[i]]+1);}}//System.out.println(Arrays.toString(dp));return dp[amount];}
}题解复盘:
class Solution {// 版本一,先遍历物品, 再遍历背包public int numSquares(int n) {int max = Integer.MAX_VALUE;int[] dp = new int[n + 1];//初始化for (int j = 0; j <= n; j++) {dp[j] = max;}//如果不想要寫for-loop填充數組的話,也可以用JAVA內建的Arrays.fill()函數。//Arrays.fill(dp, Integer.MAX_VALUE);//当和为0时,组合的个数为0dp[0] = 0;// 遍历物品for (int i = 1; i * i <= n; i++) {// 遍历背包for (int j = i * i; j <= n; j++) {//if (dp[j - i * i] != max) {dp[j] = Math.min(dp[j], dp[j - i * i] + 1);//}//不需要這個if statement,因爲在完全平方數這一題不會有"湊不成"的狀況發生( 一定可以用"1"來組成任何一個n),故comment掉這個if statement。}}return dp[n];}
}一个完美的递推公式:dp[j] = Math.min(dp[j], dp[j - i * i] + 1)
相关文章:

D3839|完全背包
完全背包: 首先01背包的滚动数组中的解法是内嵌的循环是从大到小遍历,为了保证每个物品仅被添加一次。 for(int i 0; i < weight.size(); i) { // 遍历物品for(int j bagWeight; j > weight[i]; j--) { // 遍历背包容量dp[j] max(dp[j], dp[j…...
Java之Synchronized与锁升级
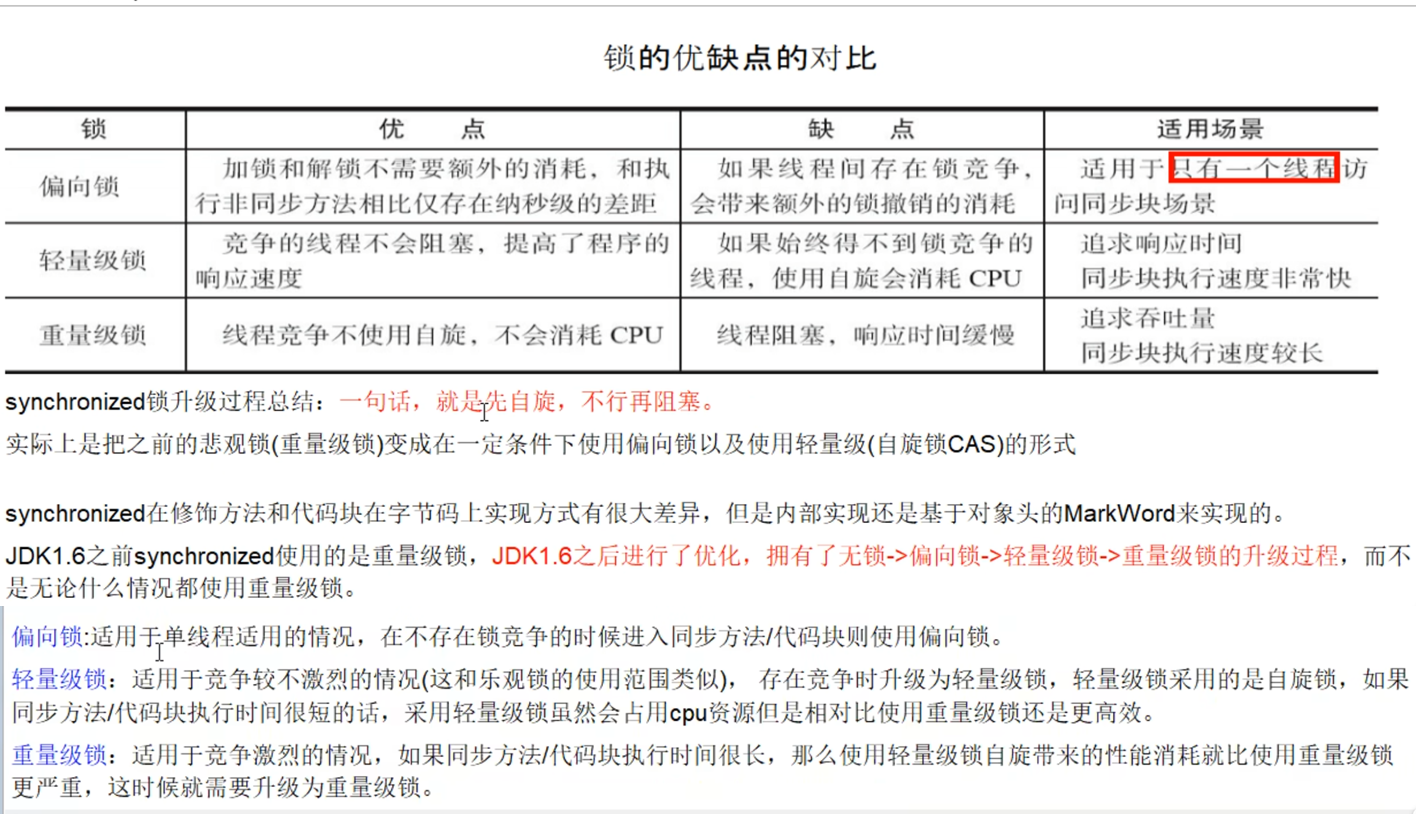
Synchronized与锁升级 一、概述 在多线程并发编程中 synchronized 一直是元老级角色,很多人都会称呼它为重量级锁。但是,随着 Java SE 1.6 对 synchronized 进行了各种优化之后,有些情况下它就并不那么重了。 本文详细介绍 Java SE 1.6 中为…...

kitex出现:open conf/test/conf.yaml: no such file or directory
open conf/test/conf.yaml: no such file or directory https://github.com/cloudwego/cwgo/issues/120 https://github.com/cloudwego/cwgo/issues/29 在使用Kitex生成的代码中,单元测试时回报错,如标题所示。出现该错的原因是,biz/servic…...

sql server多表查询
查询目标 现在有学生表和学生选课信息表,stu和stuSelect,stu中包含学生用户名、名字,stuSelect表中包含学生用户名,所选课程名 学生表: nameusername李明Li Ming李华Li Hua 学生选课表: usernameCourse…...
如何利用PPT绘图并导出清晰图片
在写论文的过程中,免不了需要绘图,但是visio等软件绘图没有在ppt上绘图比较熟练,尤其流程图结构图. 但是ppt导出的图片也不够清晰,默认分辨率是96dpi,而杂志投稿一般要求至300dpi。解决办法如下: 1.打开注…...

1.倒排索引 2.逻辑斯提回归算法
1.倒排索引 https://help.aliyun.com/zh/open-search/retrieval-engine-edition/introduction-to-inverted-indexes 倒排索引(Inverted Index)是一种数据结构,用于快速查找包含某个特定词或词语的文档。它主要用于全文搜索引擎等应用&#…...
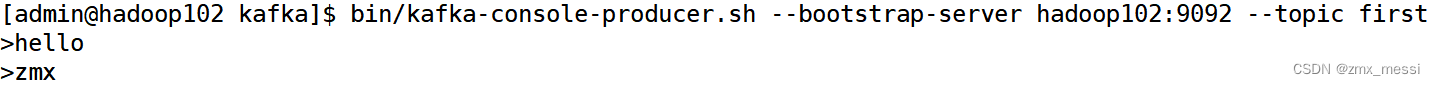
Kafka消费者组
消费者总体工作流程 Consumer Group(CG):消费者组,由多个consumer组成。形成一个消费者组的条件,是所有消费者的groupid相同。 • 消费者组内每个消费者负责消费不同分区的数据,一个分区只能由一个组内消费…...

四. 基于环视Camera的BEV感知算法-BEVDepth
目录 前言0. 简述1. 算法动机&开创性思路2. 主体结构3. 损失函数4. 性能对比总结下载链接参考 前言 自动驾驶之心推出的《国内首个BVE感知全栈系列学习教程》,链接。记录下个人学习笔记,仅供自己参考 本次课程我们来学习下课程第四章——基于环视Cam…...
——使用docker compose安装mysql)
CentOS系统环境搭建(二十五)——使用docker compose安装mysql
centos系统环境搭建专栏🔗点击跳转 文章目录 使用docker compose安装mysqlMySQL81.新建文件夹2.创建docker-compose.yaml3.创建my.cnf4.mysql容器的启动和关闭 MySQL5.71.新建文件夹2.创建docker-compose.yaml3.创建my.cnf4.mysql容器的启动和关闭 使用docker comp…...
协作机器人(Collaborative-Robot)安全碰撞的速度与接触力
协作机器人(Collaborative-Robot)的安全碰撞速度和接触力是一个非常重要的安全指标。在设计和使用协作机器人时,必须确保其与人类或其他物体的碰撞不会对人员造成伤害。 对于协作机器人的安全碰撞速度,一般会设定一个上限值&…...

第11章 GUI Page400~402 步骤二 画直线
运行效果: 源代码: /**************************************************************** Name: wxMyPainterApp.h* Purpose: Defines Application Class* Author: yanzhenxi (3065598272qq.com)* Created: 2023-12-21* Copyright: yanzhen…...

华为gre隧道全部跑静态路由
最终实现: 1、pc1能用nat上网ping能pc3 2、pc1能通过gre访问pc2 3、全部用静态路由做,没有用ospf,如果要用ospf,那么两边除了路由器上跑ospf,核心交换机也得用ospf r2配置: acl number 3000 rule 5 deny…...

【c++】入门1
c关键字 命名空间 在C/C中,变量、函数和后面要学到的类都是大量存在的,这些变量、函数和类的名称将都存在于全局作用域中,可能会导致很多冲突。使用命名空间的目的是对标识符的名称进行本地化,以避免命名冲突或名字污染ÿ…...
Python之Django项目的功能配置
1.创建Django项目 进入项目管理目录,比如:D盘 执行命令:diango-admin startproject demo1 创建项目 如果提示diango命令不存在,搜索diango-admin程序的位置,然后加入到环境变量path中。 进入项目,cd demo…...
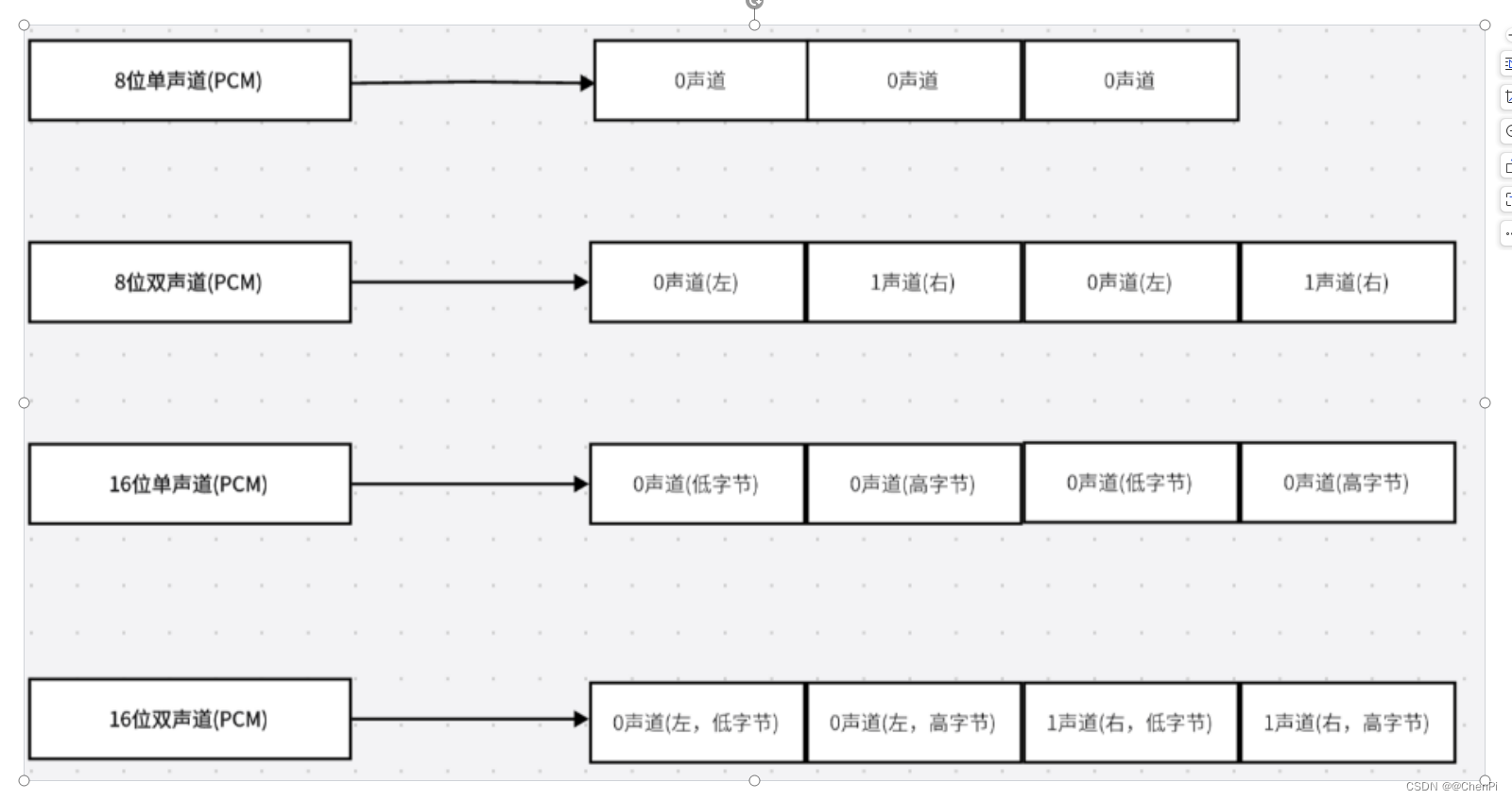
P4 音频知识点——PCM音频原始数据
目录 前言 01 PCM音频原始数据 1.1 频率 1.2 振幅: 1.3 比特率 1.4 采样 1.5 量化 1.6 编码 02. PCM数据有以下重要的参数: 采样率: 采集深度 通道数 PCM比特率 PCM文件大小计算: …...

解决Electron中WebView加载部分HTTPS页面白屏的方法
Electron是一个开源的桌面应用程序框架,它允许使用Web技术构建跨平台的桌面应用。在Electron应用中,WebView 是一个常用的组件,用于嵌套加载Web内容。然而,有时候在加载使用 HTTPS 协议的页面时,可能会因为证书问题导致…...

【Java中创建对象的方式有哪些?】
✅Java中创建对象的方式有哪些? ✅使用New关键字✅使用反射机制✅使用clone方法✅使用反序列化✅使用方法句柄✅ 使用Unsafe分配内存 ✅使用New关键字 这是我们最常见的也是最简单的创建对象的方式,通过这种方式我们还可以调用任意的构造函数 (无参的和有…...
)
npm使用详解(好吧好吧是粗解)
目录 npm是什么? npm有什么用? npm安装 在 Windows 上 在 macOS 上 在 Linux 上(使用 apt 包管理器为例) 验证 npm 安装成功: npm使用 1. 初始化项目: 2. 安装和管理依赖: 3. 查看和…...
uniapp自定义头部导航怎么实现?
一、在pages.json文件里边写上自定义属性 "navigationStyle": "custom" 二、在对应的index页面写上以下: <view :style"{ height: headheight px, backgroundColor: #24B7FF, zIndex: 99, position: fixed, top: 0px, width: 100% …...
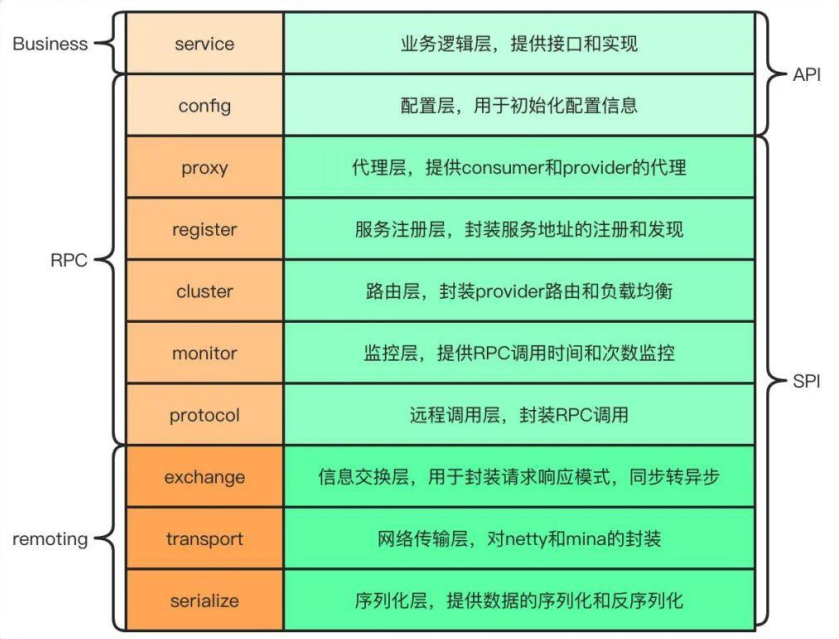
什么是 Dubbo?它有哪些核心功能?
文章目录 什么是 Dubbo?它有哪些核心功能? 什么是 Dubbo?它有哪些核心功能? Dubbo 是一款高性能、轻量级的开源 RPC 框架。由 10 层模式构成,整个分层依赖由上至下。 通过这张图我们也可以将 Dubbo 理解为三层模式&…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...

基于谷歌ADK的 智能产品推荐系统(2): 模块功能详解
在我的上一篇博客:基于谷歌ADK的 智能产品推荐系统(1): 功能简介-CSDN博客 中我们介绍了个性化购物 Agent 项目,该项目展示了一个强大的框架,旨在模拟和实现在线购物环境中的智能导购。它不仅仅是一个简单的聊天机器人,更是一个集…...
