代码随想录算法训练营第十三天 | 239. 滑动窗口最大值、347.前 K 个高频元素
239. 滑动窗口最大值
题目链接:239. 滑动窗口最大值
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
文章讲解/视频讲解:https://programmercarl.com/0239.%E6%BB%91%E5%8A%A8%E7%AA%97%E5%8F%A3%E6%9C%80%E5%A4%A7%E5%80%BC.html
思路
设置一个大小为k的队列queue。
在滑动窗口处于初始位置时,将初始的k个元素推入队列中:
如果队列为空或者当前元素小于队列的队尾元素,直接将nums[i]推入队列尾部;
如果当前元素大于队列的队尾元素,则循环判断,只要队列的队尾元素小于当前元素,就将当前队尾排出,直到循环判断结束,将nums[i]推入队列尾部。
此时队列的队首就是当前窗口的最大值。
滑动窗口开始移动时,开始对整数数组nums的后续元素进行遍历:
此时滑动窗口的范围为[i, i + k - 1],如果nums[i - 1]等于队首元素,则将队首排出,说明此时队首已经不在滑动窗口中了;
对于当前值nums[i],如果队列为空或nums[i]小于队列的队尾元素,直接将nums[i]推入队列尾部,如果此时队列大小大于k,将队首排出;
如果nums[i]大于队列的队尾元素,则开始循环判断,只要队列的队尾元素小于nums[i],就将当前队尾排出,直到循环判断结束,将nums[i]推入队列尾部。
同样的,每次遍历,当前队列的队首就是当前窗口的最大值。
上述方法在构建队列时,可以保证队列中的元素是单调非增的,因此队首就是当前窗口的最大值。同时,因为需要对队列的队尾做排出操作,用deque双向队列来作为队列的容器。
注:如果用vector作为容器,会超时。因为排出队首元素是o(n)复杂度的。
C++实现
class Solution {
public:vector<int> maxSlidingWindow(vector<int>& nums, int k) {vector<int> results;deque<int> dQ;for(int i = 0;i<k;i++){if(dQ.empty() || nums[i] <= dQ.back()){dQ.push_back(nums[i]);}else{while(!dQ.empty() && dQ.back() < nums[i]) dQ.pop_back();dQ.push_back(nums[i]);}}results.push_back(dQ.front());for(int i = k;i<nums.size();i++){if(nums[i - k] == dQ.front()) dQ.pop_front();if(dQ.empty() || nums[i] <= dQ.back()){dQ.push_back(nums[i]);if(dQ.size() > k) dQ.pop_front();}else{while(!dQ.empty() && dQ.back() < nums[i]) dQ.pop_back();dQ.push_back(nums[i]);}results.push_back(dQ.front());}return results;}
};
347.前 K 个高频元素
题目链接:347.前 K 个高频元素
给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
文章讲解/视频讲解:https://programmercarl.com/0347.%E5%89%8DK%E4%B8%AA%E9%AB%98%E9%A2%91%E5%85%83%E7%B4%A0.html
思路
用小顶堆来实现。
定义一种node结构,属性分别为值和频率。
首先遍历数组,统计每个元素的出现频率,将代表每个元素的node存入数组frequents。
定义一个存储node类型的小顶堆,堆的判断标准是node之间的频率,频率越低越靠前。
遍历数组frequents,将元素不断地push进这个小顶堆中,如果小顶堆的大小大于k,则将小顶堆的堆顶排出。
最终小顶堆中的所有元素,构成了前K个高频元素。
C++实现
struct node{int value;int frequence;
};class Solution {
public:vector<int> topKFrequent(vector<int>& nums, int k) {auto cmp = [](node a, node b){return a.frequence > b.frequence;};priority_queue<node, vector<node>, decltype(cmp)> Q(cmp);vector<node> frequents;unordered_map<int, int> hashMap;for(int i = 0;i<nums.size();i++){hashMap[nums[i]] += 1;}for(auto p : hashMap){frequents.push_back({p.first, p.second});}for(int i = 0;i<frequents.size();i++){Q.push(frequents[i]);if(Q.size() > k) Q.pop();}vector<int> results;while(!Q.empty()){results.push_back(Q.top().value);Q.pop();}return results;}
};
相关文章:

代码随想录算法训练营第十三天 | 239. 滑动窗口最大值、347.前 K 个高频元素
239. 滑动窗口最大值 题目链接:239. 滑动窗口最大值 给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回 滑动窗口中的最大值 。 文章讲解…...

推荐五个免费的网络安全工具
导读: 在一个完美的世界里,信息安全从业人员有无限的安全预算去做排除故障和修复安全漏洞的工作。但是,正如你将要学到的那样,你不需要无限的预算取得到高质量的产品。这里有SearchSecurity.com网站专家Michael Cobb推荐的五个免费…...
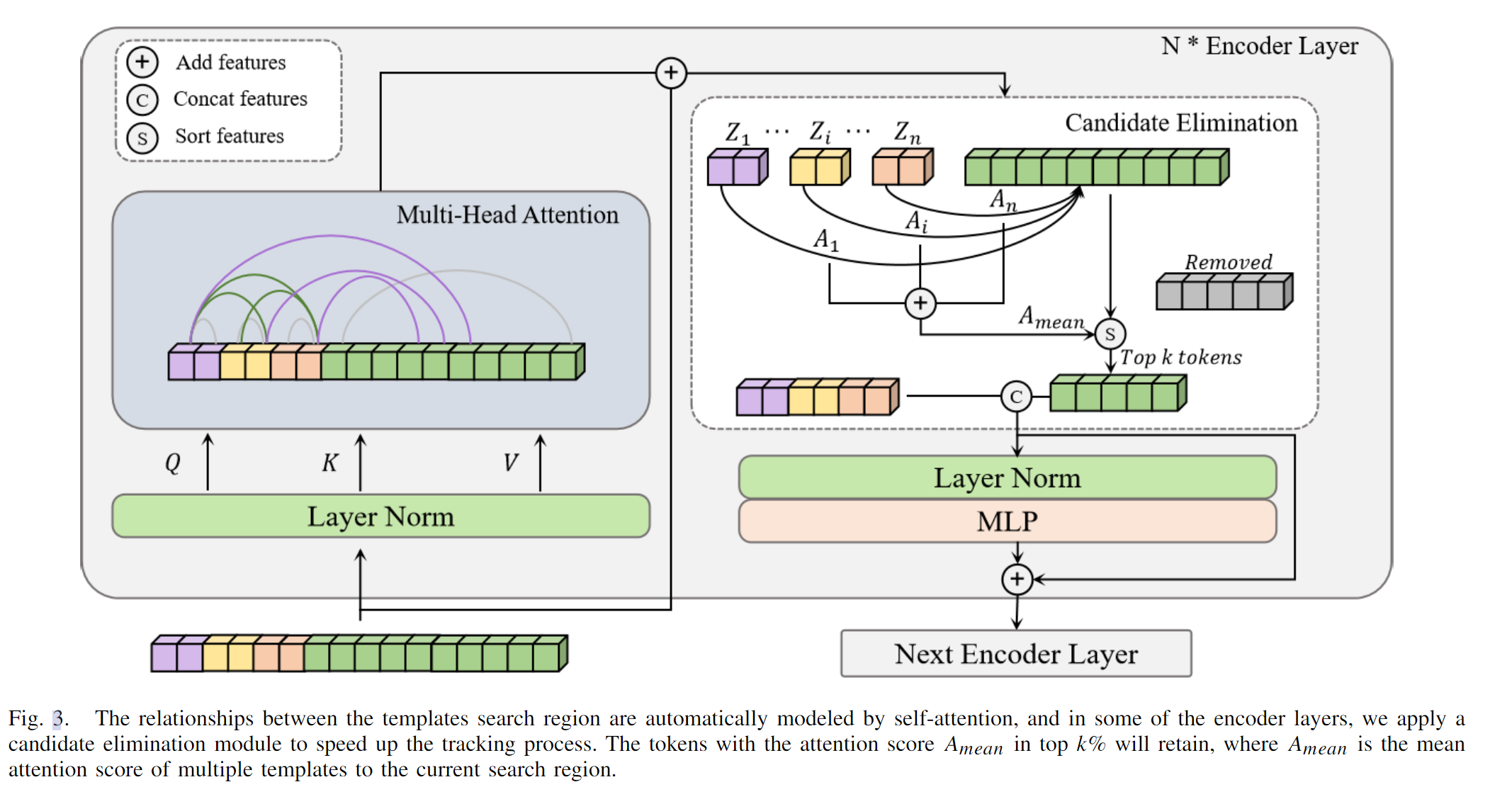
Cross-Drone Transformer Network for Robust Single Object Tracking论文阅读笔记
Cross-Drone Transformer Network for Robust Single Object Tracking论文阅读笔记 Abstract 无人机在各种应用中得到了广泛使用,例如航拍和军事安全,这得益于它们与固定摄像机相比的高机动性和广阔视野。多无人机追踪系统可以通过从不同视角收集互补的…...
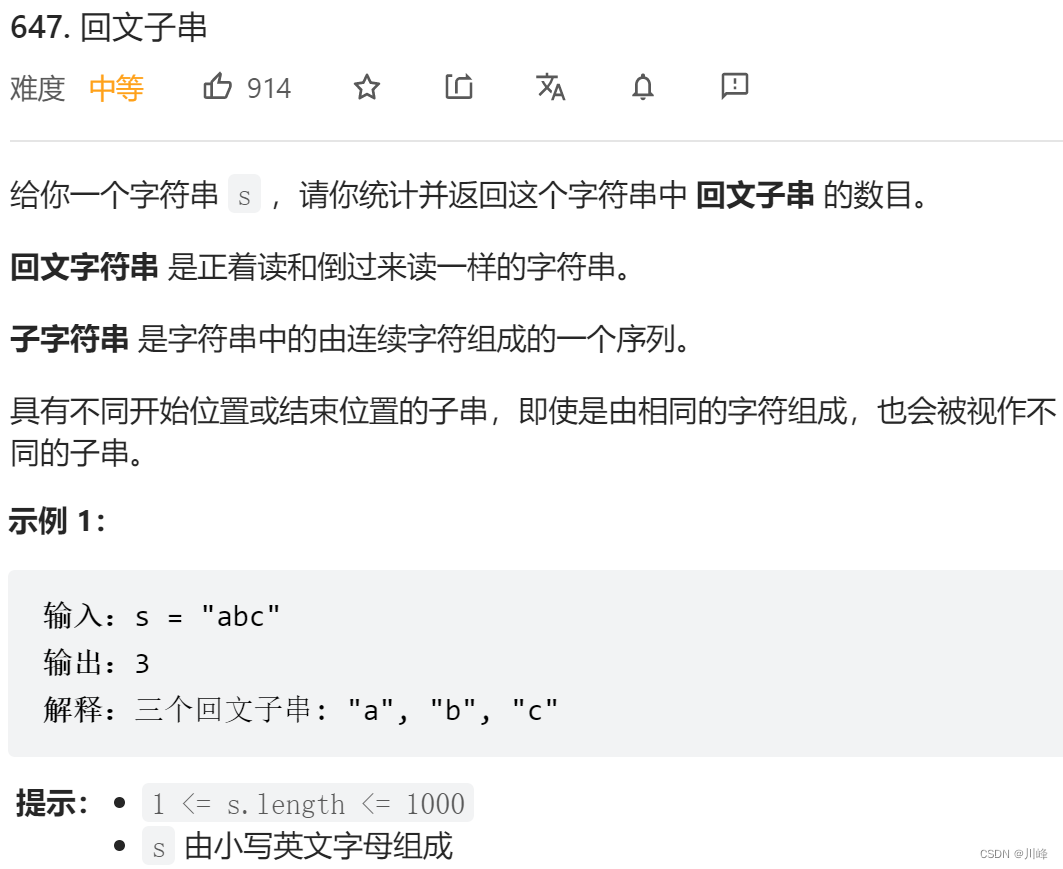
【LeetCode刷题笔记】动态规划(二)
647. 回文子串 解题思路: 1. 暴力穷举 , i 遍历 [0, N) , j 遍历 [i+1, N] ,判断每一个子串 s[i, j) 是否是回文串,判断是否是回文串可以采用 对撞指针 的方法。如果是回文串就计数 +1...

(十七)Flask之大型项目目录结构示例【二扣蓝图】
大型项目目录结构: 问题引入: 在上篇文章讲蓝图的时候我给了一个demo项目,其中templates和static都各自只有一个,这就意味着所有app的模板和静态文件都放在了一起,如果项目比较大的话,这就非常乱…...

蓝牙技术在物联网中的应用
随着蓝牙技术的不断演进和发展,蓝牙已经从单一的传统蓝牙技术发展成集传统蓝牙。高速蓝牙和低耗能蓝牙于一体的综合技术,不同的应用标准更是超过40个越来越广的技术领域和越来越多的应用场景,使得目前的蓝牙技术成为包含传感器技术、识别技术…...
宝塔面板Linux服务器CentOS 7数据库mysql5.6升级至5.7版本教程
近段时间很多会员问系统更新较慢,也打算上几个好的系统,但几个系统系统只支持MYSQL5.7版本,服务器一直使用较低的MYSQL5.6版本,为了测试几个最新的系统打算让5.6和5.7并存使用,参考了多个文档感觉这种并存问题会很多。…...

掌握常用Docker命令,轻松管理容器化应用
Docker是一个开源的应用容器引擎,它可以让开发者将应用程序及其依赖打包到一个轻量级、可移植的容器中,然后发布到任何流行的Linux机器或Windows机器上,也可以实现虚拟化。容器是完全使用沙箱机制,相互之间不会有任何接口。下面介…...
(c++,multiset做法))
【数据结构1-2】P5076 普通二叉树(简化版)(c++,multiset做法)
文章目录 一、题目【深基16.例7】普通二叉树(简化版)题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1基本思路: 一、题目 【深基16.例7】普通二叉树(简化版) 题目描述 您需要写一种数据结构,来维…...

Linux系统安装及管理
目录 一、Linux应用程序基础 1.1应用程序与系统命令的关系 1.2典型应用程序的目录结构 1.3常见的软件包装类型 二、RPM软件包管理 1.RPM是什么? 2.RPM命令的格式 2,1查看已安装的软件包格式 2.2查看未安装的软件包 3.RPM安装包从哪里来? 4.挂…...
MySQL学生向笔记以及使用过程问题记录(内含8.0.34安装教程
MySQL 只会写代码 基本码农 要学好数据库,操作系统,数据结构与算法 不错的程序员 离散数学、数字电路、体系结构、编译原理。实战经验, 高级程序员 去IOE:去掉IBM的小型机、Oracle数据库、EMC存储设备,代之以自己在开源…...

obs video-io.c
video_frame_init 讲解 /* messy code alarm video_frame_init 函数用于初始化视频帧。它接受一个指向 struct video_frame 结构体的指针 frame, 视频格式 format,以及宽度 width 和高度 height。该函数根据视频格式的不同,计算出每个视频帧…...

简述 tcp 和 udp的区别?
简述 tcp 和 udp的区别? TCP(Transmission Control Protocol)和UDP(User Datagram Protocol)是两种不同的传输层协议,用于在计算机网络中进行数据传输。以下是它们的主要区别: 区别࿱…...

信息收集 - 谷歌hack
搜索引擎 FOFA网络空间测绘:https://fofa.info/ FOFA(FOcus on Assets)是一个网络空间搜索引擎,可以帮助用户快速定位和收集特定目标的信息。 ZoomEye:https://www.zoomeye.org ZoomEye 是一个网络空间搜索引擎,可以用于发现和收集特定目标的网络设备、Web应用程序、开放…...
应用实战项目二(实现旋变软解码))
英飞凌TC3xx之一起认识DSADC系列(七)应用实战项目二(实现旋变软解码)
英飞凌TC3xx之一起认识DSADC系列(七) 1 项目要求2 项目实现2.1 内部时钟配置2.2 输入信号配置2.3 调制器配置2.4 滤波器链路配置2.5 整流器配置3 总结本文写一篇关于DSADC的resover的载波信号生成的应用,刚刚接触DSADC的开发者很容易被手册中简短的文字描述弄的迷惑,它到底…...
【浏览器】同源策略和跨域
1. 什么是跨域 在说跨域之前,先说说同源策略,什么是同源策略呢?同源策略是浏览器的一种安全机制,减少跨站点脚本攻击(XSS,Cross Site Scripting)、跨站点请求伪造(CSRF,Cross Site Request Forgery)攻击等,因为非同源的请求会被浏览器拦截掉。 同源就是协议、域名(…...

云计算与大数据之间的羁绊(期末不挂科版):云计算 | 大数据 | Hadoop | HDFS | MapReduce | Hive | Spark
文章目录 前言:一、云计算1.1 云计算的基本思想1.2 云计算概述——什么是云计算?1.3 云计算的基本特征1.4 云计算的部署模式1.5 云服务1.6 云计算的关键技术——虚拟化技术1.6.1 虚拟化的好处1.6.2 虚拟化技术的应用——12306使用阿里云避免了高峰期的崩…...

基于jdk11和基于apache-httpclient的http请求工具类
1.基于apache-httpclient 需要引入依赖 <dependency><groupId>org.apache.httpcomponents</groupId><artifactId>httpclient</artifactId><version>4.3.5</version></dependency> 工具类如下: package com.bw.e…...

Node.js(二)-模块化
1. 模块化的基本概念 1.1 什么是模块化 模块化是指解决一个复杂问题时,自顶向下逐层将系统拆分成若干模块的过程。对于整个系统来说,模块是可组合、分解和更换的单元。 1.2 编程领域中的模块化 编程领域中的模块化,就是遵守固定的规则&…...
)
ARM AArch64的TrustZone架构详解(上)
目录 一、概述 1.1 在开始之前 二、什么是TrustZone? 2.1 Armv8-M的TrustZone 2.2 Armv9-A Realm Management Extension(RME)...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...
