【数据结构】什么是二叉树?
🦄个人主页:修修修也
🎏所属专栏:数据结构
⚙️操作环境:Visual Studio 2022

目录
📌二叉树的定义
📌二叉树的特点
📌特殊二叉树
📌二叉树的性质
📌二叉树的存储结构
📌二叉树的遍历
前序遍历
中序遍历
后序遍历
层序遍历
结语
📌二叉树的定义
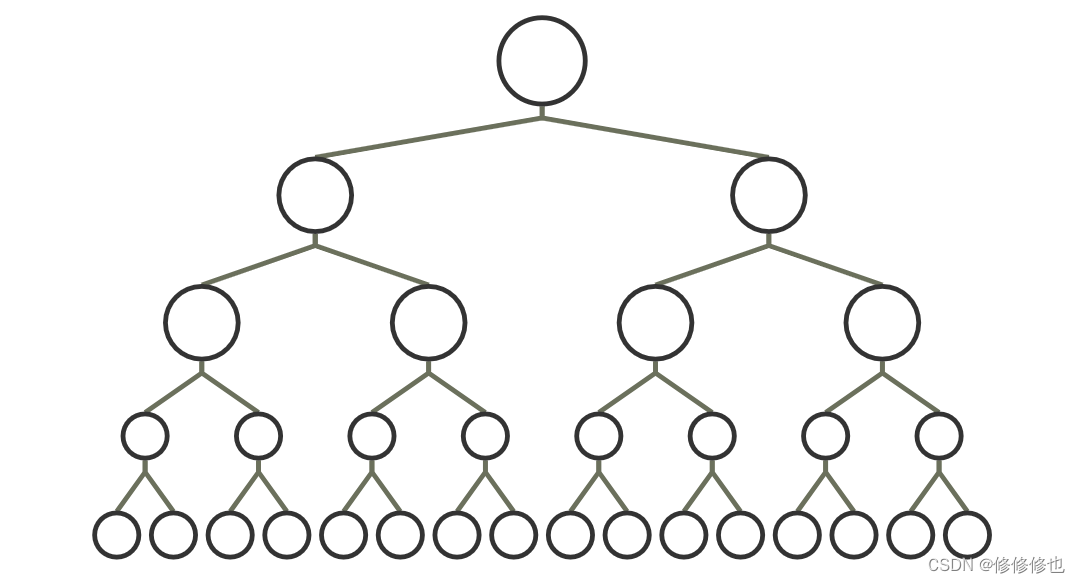
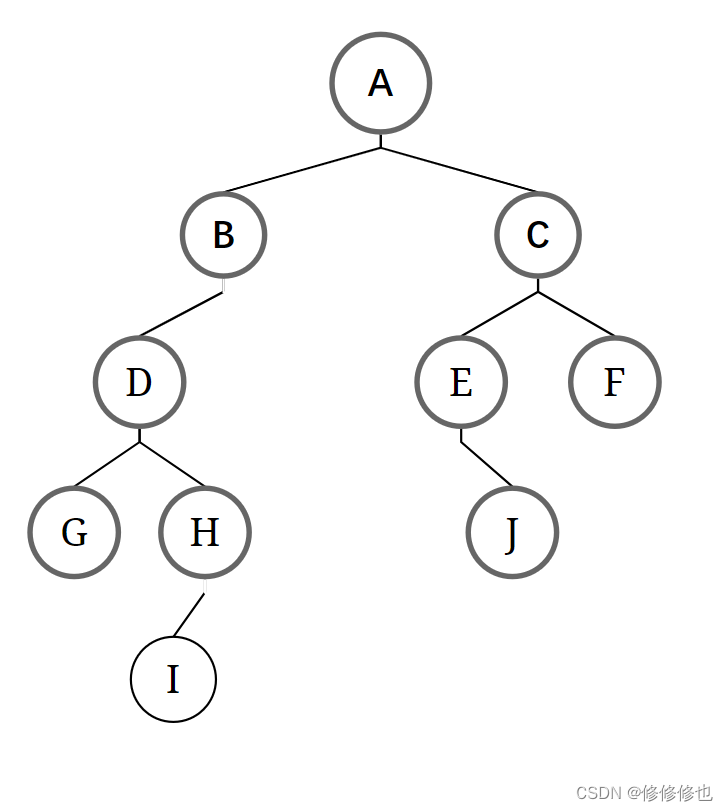
二叉树(Binary Tree)是n(n≥0)个结点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根结点和两颗互不相交的,分别称为根结点的左子树和右子树的二叉树组成.
二叉树逻辑结构如下图所示:
📌二叉树的特点
二叉树的特点有:
- 每个结点最多有两棵子树,所以二叉树中不存在度大于2的结点.注意不是只有两颗子树,而是最多有.没有子树或者有一颗子树都是可以的.
- 左子树和右子树是有顺序的,次序不能任意颠倒.
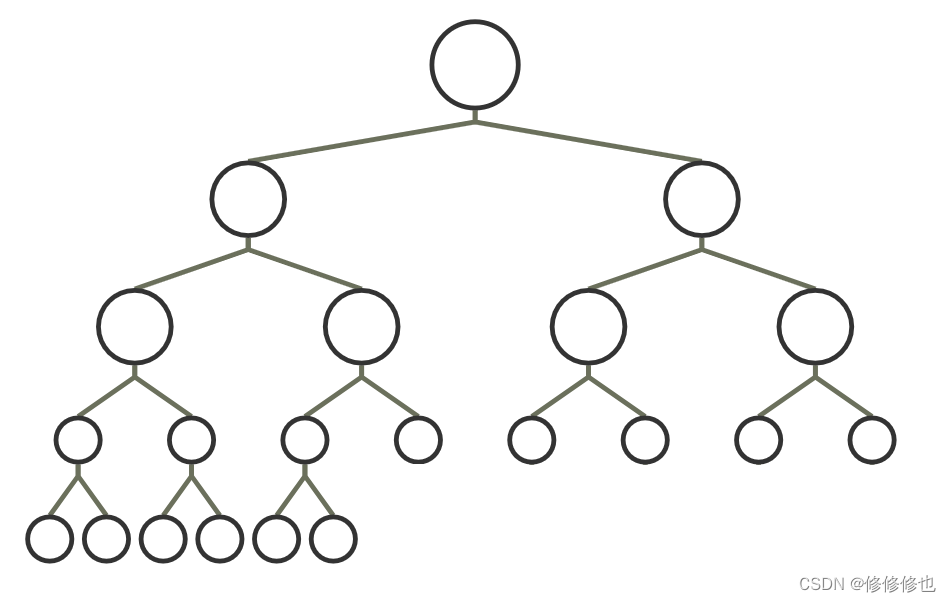
- 即使树中某个结点只有一棵子树,也要区分它是左子树还是右子树.下图中树1和树2是同一颗树,但它们却是不同的二叉树:
二叉树具有五种基本形态:
- 空二叉树.
- 只有一个根结点.
- 根结点只有左子树.
- 根结点只有右子树.
- 根结点既有左子树又有右子树.
只有三个结点的二叉树,有几种形态?
答案是有以下5种形态:
📌特殊二叉树
- 斜树
所有的结点都只有左子树的二叉树叫左斜树.所有结点都是只有右子树的二叉树叫右斜树.这两者统称为斜树.上图中的树2就是左斜树,树3就是右斜树.
斜树每一层只有一个结点,结点的个数与二叉树的深度相同.
- 满二叉树
在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树.
如下图所示,该树就是一颗满二叉树:
注意,单是每个结点都存在左右子树,不能算是满二叉树,还必须要所有的叶子都在同一层上,这就做到了整棵树的平衡.
因此,满二叉树的特点有:
- 叶子只能出现在最下一层.出现在其他层就不可能达成平衡.
- 非叶子节点的度一定是2.
- 在同样深度的二叉树中,满二叉树的结点个数最多,叶子数最多.
- 完全二叉树
对一颗具有n个结点的二叉树按层序编号,如果编号为i(1≤i≤n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,则这颗二叉树称为完全二叉树,如下图所示:
完全二叉树的特点有:
- 叶子结点只能出现在最下两层.
- 最下层的叶子一定集中在左部连续位置.
- 倒数二层,若有叶子结点,一定都在右部连续位置.
- 如果结点度为1,则该结点只有左孩子,即不存在只有右子树的情况.
- 同样结点数的二叉树,完全二叉树的深度最小.
📌二叉树的性质
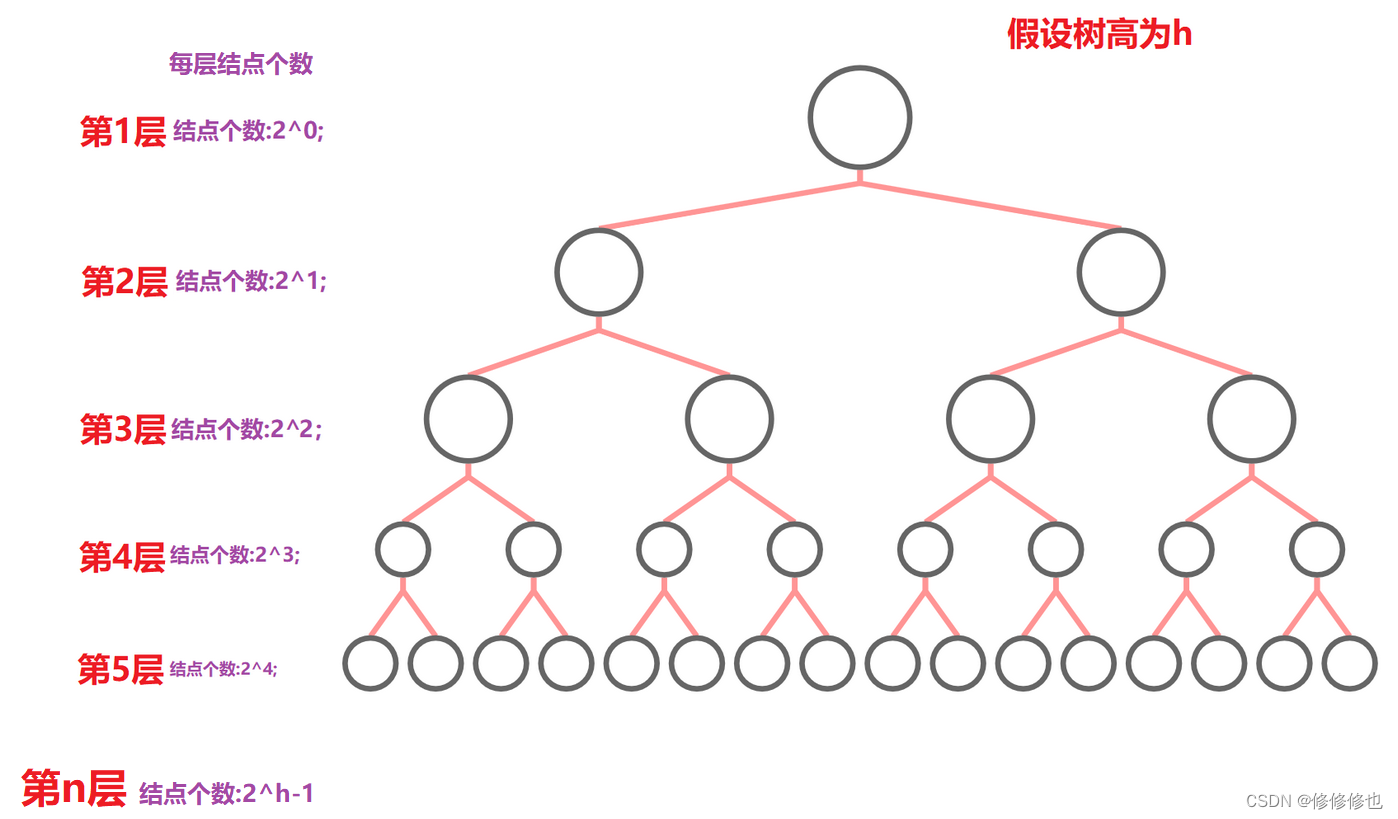
性质1:
在二叉树的第i层上至多有
个结点(i≥1).
推导如下:
性质2:
深度为k的二叉树至多有
个结点(k≥1).
推导如下:
性质3:
对任何一颗二叉树T,如果其终端结点数为,度为2的结点数为
,则
.
终端结点数其实就是叶子节点数,一颗二叉树,只会存在度为0,度为1,度为2的结点,我们假设度为1的节点数为
,则树T结点总数
.
性质4:
具有n个结点的完全二叉树的深度为
, (
表示不大于x的最大整数).
我们由满二叉树的定义可知,深度为k的满二叉树的结点数n一定是
.因为这是最多的结点个数.那么对于
倒推可得满二叉树的深度数为
.
而对于完全二叉树而言,它的节点数一定少于等于同样深度数的满二叉树的结点数
,但一定多于
.即满足
.易推导得
.
性质5:
如果对一颗有n个结点的完全二叉树(其深度为
)的结点按层序编号(从第1层到第
层,每层从左到右),对任一结点i(1≤i≤n)有:
- 如果i=1,则结点i是二叉树的根,无双亲;如果i>1,则其双亲是结点
.
- 如果2*i>n,则结点i无左孩子(结点i为叶子结点);否则其左孩子是结点2*i.
- 如果2*i+1>n,则结点i无右孩子;否则其右孩子是结点2*i+1.
📌二叉树的存储结构
- 顺序存储结构
二叉树的顺序存储结构就是用一维数组存储二叉树中的结点,并且结点的存储位置,也就是数组的下标要能体现结点之间的逻辑关系.
先来看看完全二叉树的顺序存储,一颗完全二叉树如下图:
将这颗二叉树存到数组中,相应的下标对应其同样的位置:
但如果遇到树中不存在的结点,我们也可在顺序结构中存入"^"或空,来表示该结点不存在:
这种顺序存储结构仅适用于完全二叉树.因为,在最坏的情况下,一个深度为k且只有k个结点的单支树(即树中不存在度为2的结点)却需要长度为
的一维数组:
- 二叉链表
因为二叉树每个结点最多有两个孩子,所以为它的结点设计一个数据域和两个指针域,分别指向两个孩子,我们称这样的链表叫做二叉链表.
结点结构图如下:
二叉链表结构定义代码如下:
typedef struct BiTNode {TElemType data; //数据域struct BiTNode*left; //左孩子指针域struct BiTNode*right; //右孩子指针域 }BiTNode;
📌二叉树的遍历
二叉树的遍历(traversing binary tree)是指从根节点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次且只访问一次.
前序遍历
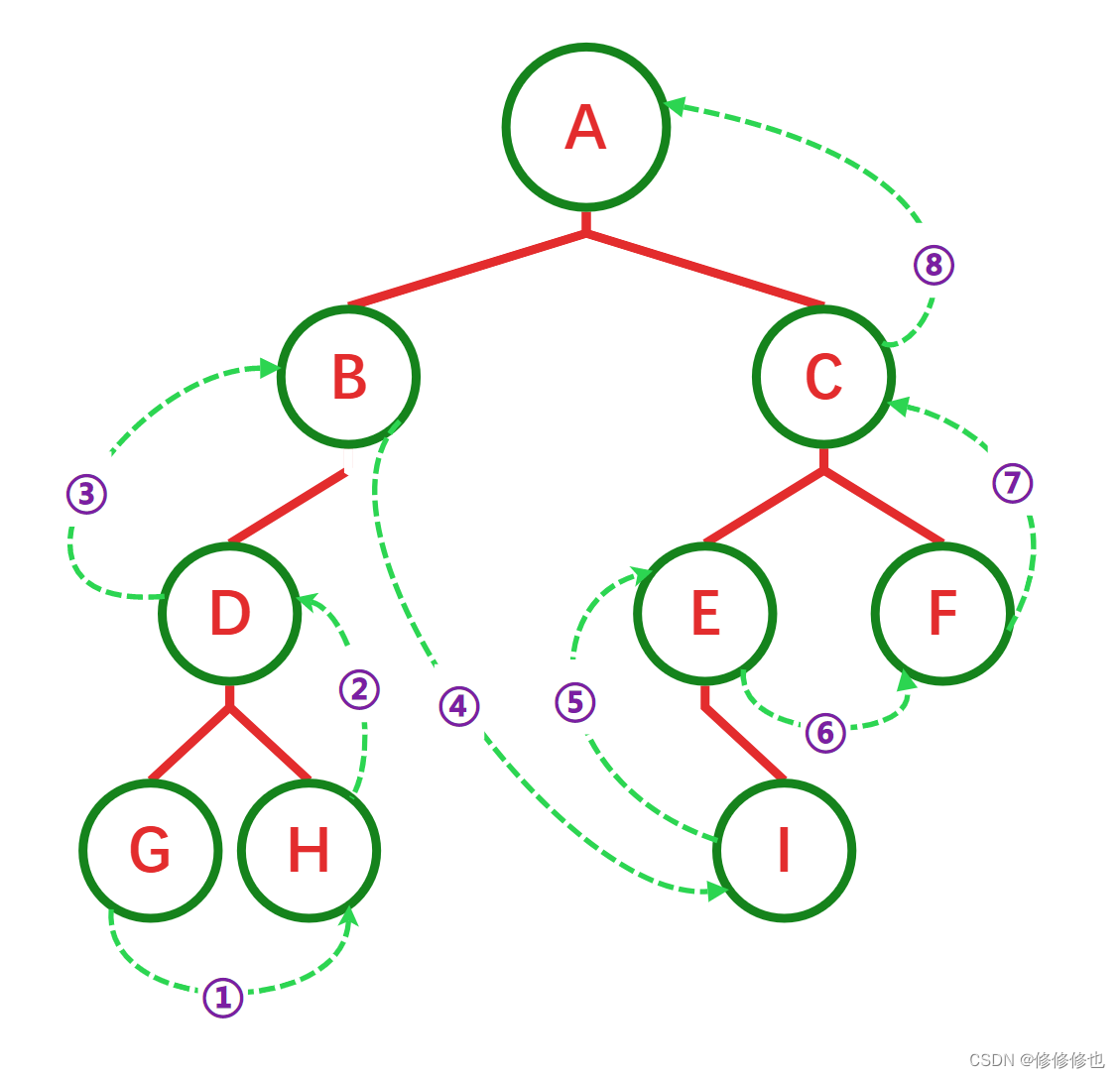
前序遍历的规则是:若二叉树为空,则空操作返回,否则先访问根节点,然后前序遍历左子树,再前序遍历右子树.
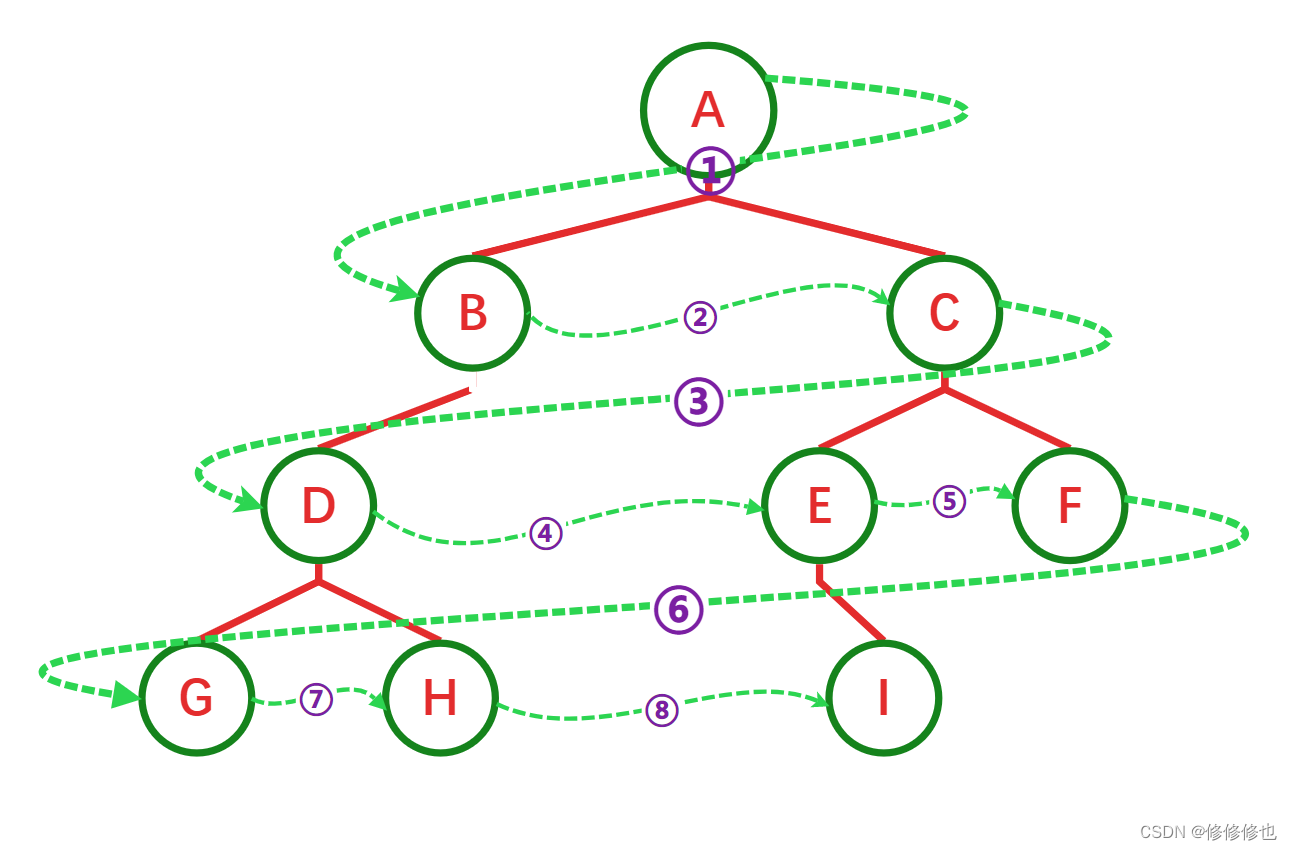
如下图所示,遍历的顺序为:ABDGHCEIF
中序遍历
中序遍历的规则是:若二叉树为空,则空操作返回,否则从根节点开始(注意不是先访问根节点)先中序遍历根节点的左子树,然后访问根节点,最后中序遍历右子树.
如下图所示,遍历的顺序为:GDHBAEICF
后序遍历
后序遍历的规则是:若二叉树为空,则空操作返回,否则从左到右先叶子后结点的方式遍历访问左右子树,最后是访问根节点.
如下图所示,遍历的顺序为:GHDBIEFCA
层序遍历
层序遍历的规则是:若二叉树为空,则空操作返回,否则从树的第一层,也就是根节点开始访问,从上而下逐层遍历,在同一层中,按从左到右的顺序对结点逐个访问.
如下图所示,遍历的顺序为:ABCDEFGHI
结语
希望这篇二叉树的介绍能对大家有所帮助,欢迎大佬们留言或私信与我交流.
学海漫浩浩,我亦苦作舟!关注我,大家一起学习,一起进步!
相关文章推荐
【数据结构】什么是树?
【数据结构】什么是线性表?
【数据结构】什么是栈?
【数据结构】用C语言实现顺序栈(附完整运行代码)
【数据结构】深入浅出理解链表中二级指针的应用
【数据结构】10道经典面试题目带你玩转链表

相关文章:

【数据结构】什么是二叉树?
🦄个人主页:修修修也 🎏所属专栏:数据结构 ⚙️操作环境:Visual Studio 2022 目录 📌二叉树的定义 📌二叉树的特点 📌特殊二叉树 📌二叉树的性质 📌二叉树的存储结构 📌二叉树…...
C#教程(四):多态
1、介绍 1.1 什么是多态 在C#中,多态性(Polymorphism)是面向对象编程中的一个重要概念,它允许不同类的对象对同一消息做出响应,即同一个方法可以在不同的对象上产生不同的行为。C#中的多态性可以通过以下几种方式实现…...
电力系统风储联合一次调频MATLAB仿真模型
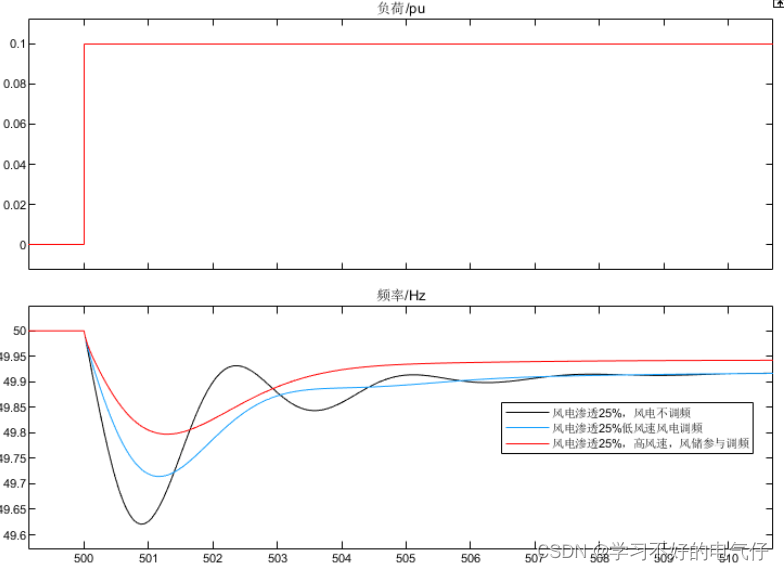
微❤关注“电气仔推送”获得资料(专享优惠) 简介: 同一电力系统在不同风电渗透率下遭受同一负荷扰动时,其频率变化规律所示: (1)随着电力系统中风电渗透率的不断提高,风电零惯性响…...

《PCI Express体系结构导读》随记 —— 内容与作者简介
本书内容介绍 本书讲述了PCI与PCI Express总线相关的最为基础的内容,并介绍了一些必要的、与PCI总线相关的处理器体系结构知识,这也是本书的重点所在。深入理解处理器体系结构是理解PCI与PCI Express总线的重要基础。 读者通过对本书的学习,…...

C#字典和列表转LuaTable
C#字典和列表转LuaTable 将C#Dictionary转成luaTable将C#List转成luaTable 将C#Dictionary转成luaTable function DicToLuaTable(Dic)--将C#的Dic转成Lua的Tablelocal dic {}if Dic thenlocal iter Dic:GetEnumerator()while iter:MoveNext() dolocal k iter.Current.Keylo…...
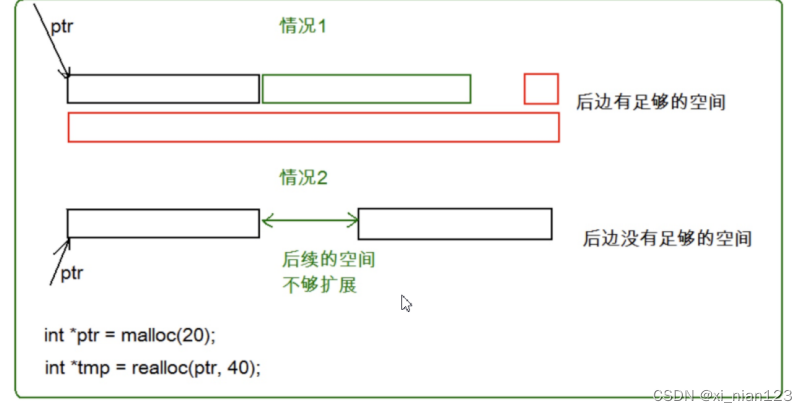
动态内存管理(1)
目录 1. 为什么存在动态内存分配 2. 动态内存函数的介绍 2.2 calloc 2.3 realloc 3. 常见的动态内存错误 3.1 对NULL指针的解引用操作 3.2 对动态开辟空间的越界访问 3.3 对非动态开辟内存使用free释放 3.4 使用free释放一块动态开辟内存的一部分 3.5 对同一块动…...
ThunderSearch(闪电搜索器)_网络空间搜索引擎工具_信息收集
文章目录 ThunderSearch简介1 项目地址2 使用方式2.1 配置文件config.json说明2.2 构建和运行 3 使用式例 ThunderSearch简介 ThunderSearch(闪电搜索器)是一款使用多个(【支持Fofa、Shodan、Hunter、Zoomeye、360Quake网络空间搜索引擎】网络空间搜索引…...
Topaz Video AI 视频修复工具(内附安装压缩包win+Mac)
目录 一、Topaz Video AI 简介 二、Topaz Video AI 安装下载 三、Topaz Video AI 使用 最近玩上了pika1.0和runway的图片转视频,发现生成出来的视频都是有点糊的,然后就找到这款AI修复视频工具 Topaz Video AI。 一、Topaz Video AI 简介 Topaz Video…...

android内存管理机制概览
关于作者:CSDN内容合伙人、技术专家, 从零开始做日活千万级APP。 专注于分享各领域原创系列文章 ,擅长java后端、移动开发、人工智能等,希望大家多多支持。 目录 一、导读二、概览三、相关概念3.1 垃圾回收3.2 应用内存的分配与回…...

下载MySQL Connector/C++
MySQL :: Download Connector/C...

ai gpt 鸡皮剔提问技巧
请将如下AB两组信息逐个匹配上的进行同类归类,用json格式输出: A:苹果 电脑 汽车 B: 猕猴桃 笔记本 根据你的要求,逐个匹配 A 组和 B 组的元素,并以 JSON 格式输出同类的归类信息: json { "匹配信息"…...

详谈 springboot整合shiro
背景: 本章将进一步的落地实践学习,在springboot中如何去整合shrio,整个过程步骤有个清晰的了解。 利用Shiro进行登录认证主要步骤: 1. 添加依赖:首先,在pom.xml文件中添加Spring Boot和Shiro的相关依赖…...
)
备忘录模式(Memento)
备忘录模式(Memento Pattern)是一种行为型设计模式,允许在不破坏封装的前提下捕获并保存一个对象的内部状态,以便在以后可以将该对象恢复到原先保存的状态。 备忘录模式通常涉及以下几个角色: 发起人(Originator):创建一个含有其当前状态的备忘录对象,并可以使用备忘录…...

【RocketMQ每日一问】consumeGroup心跳内容是什么样的?
消费者组:消费者所在的消费者组名称。这个信息用于确保同一个消费者组内的消费者不会重复地消费相同的消息。MessageModel:消息模型,可能的值为集群消费或广播消费。ConsumeType:消费类型,可能的值有"主动消费&qu…...

yolov5知识蒸馏
参考代码:https://github.com/Adlik/yolov5 https://cloud.tencent.com/developer/article/2160509 yolov5间的模型蒸馏,相同结构的。 配置参数 parser.add_argument(--t_weights, typestr, default./weights/yolov5s.pt,helpinitial teacher model wei…...
HUAWEI华为笔记本电脑MateBook D 14 2022款 i5 集显 非触屏(NbDE-WFH9)原装出厂Windows11系统21H2
链接:https://pan.baidu.com/s/1-tCCFwZ0RggXtbWYBVyhFg?pwdmcgv 提取码:mcgv 华为MageBookD14原厂WIN11系统自带所有驱动、出厂状态主题壁纸、Office办公软件、华为电脑管家、华为应用市场等预装软件程序 文件格式:esd/wim/swm 安装方式…...

微服务-springcloud(eureka实践, nacos实践)
Spring 体系图 版本关系 eureka 实践 1 父工程依赖 <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>2.6.14</version> </parent> <dependencyManage…...

Hadoop入门学习笔记——五、在虚拟机中部署Hive
视频课程地址:https://www.bilibili.com/video/BV1WY4y197g7 课程资料链接:https://pan.baidu.com/s/15KpnWeKpvExpKmOC8xjmtQ?pwd5ay8 Hadoop入门学习笔记(汇总) 目录 五、在虚拟机中部署Hive5.1. 在node1虚拟机安装MySQL5.2.…...

用Nest 实现大文件分片上传,加速工作效率神器
文件上传是常见需求,只要指定 content-type 为 multipart/form-data,内容就会以这种格式被传递到服务端: 服务端再按照 multipart/form-data 的格式提取数据,就能拿到其中的文件。 但当文件很大的时候,事情就变得不一样…...

将ncnn及opencv的mat存储成bin文件的方法
利用fstream,将ncnn及opencv的mat存储成bin文件。 ncnn::Mat to bin std::ios::binary标志指示文件以二进制模式进行读写, std::ofstream file("output_x86.bin", std::ios::binary); 将input_mat中的宽、高和通道数分别赋值给width、heig…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...