Verilog实现组合逻辑电路
在verilog 中可以实现的数字电路主要分为两类----组合逻辑电路和时序逻辑电路。
组合逻辑电路比较简单,仅由基本逻辑门组成---如与门、或门和非门等。当电路的输入发生变化时,输出几乎(信号在电路中传递时会有一小段延迟)立即就发生变化。
相反,时序逻辑电路使用时钟且必须要触发器等存储元件,所以其输出变化与电路时钟同步,不是即时变化的。
这篇文章将讨论如何使用 assign 关键字在 verilog 中实现连续赋值(continuous assignment),以及使用连续赋值语句实现基本逻辑门和多路选择器。
1、Verilog 中的连续赋值(Continuous Assignment)
设计者可以使用连续赋值语句将数据驱动到设计中的net类型中。因此,连续赋值语句经常被用来实现组合逻辑电路。
实际上可以使用两种不同的方法在verilog中实现连续赋值。第一个被称为显式(explicit)连续赋值,这是verilog中最常用的连续赋值方法;此外还可以使用隐式(implicit)连续赋值,或者叫:net声明赋值。这种方法不太常见,但它要写的代码更少。
1.1、显式连续赋值(Explicit Continuous Assignment)
使用assign关键字进行连续赋值的方法被称为显式连续赋值。下面的 verilog 代码展示了使用 assign 关键字进行连续赋值的一般语法。
assign <variable> = <value>;<variable> 是要为其分配数据的信号的名称,只能使用连续赋值的方式来给net类型的变量赋值。
<value> 可以是一个固定值或者是某个表达式,在此表达式中可以使用变量或net类型。
使用连续赋值时,只要 <value> 中的一个信号改变状态,<variable> 值就会立即发生改变。
下面的代码片段展示了一个最基本的 verilog 连续赋值示例。在该示例中,只要 b 信号改变状态,a 的值就会立即更新,使其等于 b。
assign a = b;1.2、线网声明赋值(Net Declaration Assignment)
设计者还可以在 verilog 设计中使用隐式连续赋值,这种方法通常也被称为线网(net)声明赋值。使用线网声明赋值时,只需要在声明信号的语句中写一条连续赋值语句,这可以减少代码行数。
在 verilog 中使用线网声明赋值时,需要在声明信号时使用 = 符号为信号赋值。下面的代码片段展示了线网声明赋值的一般语法。
<type> <variable> = <value>;<variable>和<value>使用方法与显式连续赋值中一致。
下面的 verilog 代码展示了如何使用线网声明赋值将 b 的值赋给信号 a。
wire a = b;2、 在Verilog 中实现组合逻辑电路
使用连续赋值语句和运算符,即可实现基本的组合逻辑电路。
下图是一个3输入与门的示例:
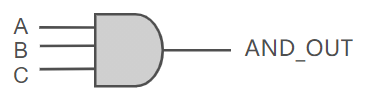
为了在 verilog 中实现该电路,可以使用 assign 关键字将数据驱动到 and_out 输出。这意味着 and_out 信号必须声明为net(线网)类型,例如wire ,然后可以使用按位与运算符 (&) 来实现基本的与门。
下面的代码片段展示了如何实现这个3输入与门。
assign and_out = a & b & c;这个例子展示了在 verilog 中设计基本的组合逻辑电路是多么的简单。如果设计者需要更改逻辑门的功能,只需要使用不同的verilog运算符即可。又或者设计者需要构建更复杂的组合逻辑电路,那么也可以混合使用不同的位运算符。为了证明这一点,将以下面的电路作为示例。
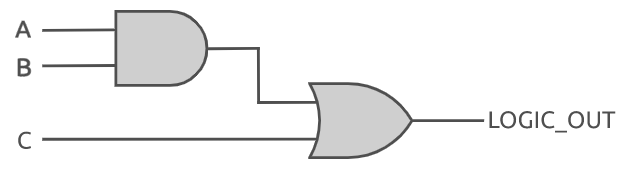
要在 verilog 中实现电路,需要混合使用按位与 (&) 运算符 和 按位或 (|) 运算符。下面的代码片段展示了如何在 verilog 中实现这一点。
assign logic_out = (a & b) | c;这段代码同样不难理解。但是设计者需要确保使用了括号来实现复杂的逻辑电路。这不仅可以确保电路正常运行,还可以让代码更易于阅读和维护。
2.1、在 Verilog 中实现多路选择器(Multiplexors)
多路选择器是组合逻辑电路中一个常用的组件。在 verilog 中,设计者可以通过多种方式实现这些组件,其中一种方法使用称为always块(always block)的结构,此语法通常被用来实现时序逻辑电路,但同时也可以实现组合逻辑电路。
2.1.1、Verilog 条件运算符
verilog中有一个与C语言等编程语言类似功能的条件运算符。要使用条件运算符,需要在 ? 表达式前写一个逻辑表达式,然后判断它是真还是假。根据表达式的真假,将两个值中的某一个赋值给输出。
下面的 verilog 代码展示了条件运算符使用的一般语法。
output = <expression> ? <value if true> : <value if false>;接下来看一个简单的 2选1的多路选择器的例子,如下面的电路图所示。
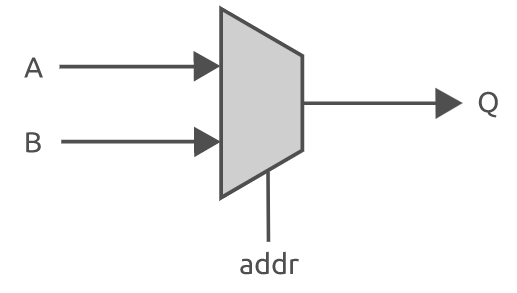
下面的代码片段清楚地展示了如何使用条件运算符在 verilog 中实现上图中的多路选择器。
assign q = addr ? b : a;2.1.2、嵌套的条件运算符(Nested Conditional Operators)
虽然这并不常见,但设计者也可以使用嵌套的条件运算符(Nested Conditional Operators)来编写代码,以实现更大的多路选择器。
接下来将以一个4选1多路选择器为例进行说明,如下图电路所示。
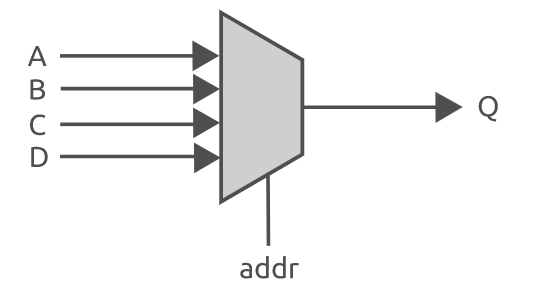
为了使用条件运算符在 verilog 中实现此电路,可以将该多路选择器视为一对2选1的多路选择器。这意味着其中一个多路选择器将在输入 A 和 B 之间进行选择,而另一个多路选择器则在输入 C 和 D 之间进行选择。这两个多路选择器都使用地址信号的 LSB 作为地址引脚。
assign mux1 = addr[0] ? b : a;
assign mux2 = addr[0] ? d : c;要实现完整的4选1多路选择器,还需要另一个多路选择器。这个多路选择器将前两个多路选择器的输出作为输入,并使用地址信号的 MSB 在它们之间进行选择。
下面的代码片段展示了实现该功能的方法。
assign q = addr[1] ? mux2 : mux1;此代码使用了在上一个示例中定义的信号 mux1 和 mux2,但其实设计者也可以从此代码中删除 mux1 和 mux2 信号,作为替代使用嵌套的条件运算符,这可以有效地减少代码行数。
下面的代码片段展示了如何做到这一点。
assign q = addr[1] ? (addr[0] ? d : c) : (addr[0] ? b : a);从这个例子也可以看出,使用条件运算符在 verilog 中实现多路选择器时,代码会变得难以阅读和理解。因此,设计者最好只使用这种方法来实现小型的多路选择器。
2.1.3、用数组(Arrays)作为多路选择器
设计者也可以使用verilog中的数组来构建简单的多路选择器。为此,可以将所有多路选择器的输入组合成一个数组,并使用地址指向数组中的元素。
为了更好地了解它是如何在实践中运用的,仍然以一个4选1的多路选择器为例。
首先需要将输入信号组合成一个数组,有两种方式可以做到这一点。第一种:先声明一个数组,然后给数组中的每一位赋值,如下面的 verilog 代码所示。
assign in_vec[0] = a;
assign in_vec[1] = b;
assign in_vec[2] = c;
assign in_vec[3] = d;第二种:可以使用verilog中的拼接运算符 { },这样就可以在一行代码中对整个数组赋值----使用一对花括号 { } 并在其中列出希望包含在数组中的所有元素。在使用拼接运算符时,如果是使用的net类型,那么也可以在一条语句中声明和赋值。
下面的 verilog 代码展示了如何使用拼接运算符来对数组赋值。
assign in_vec = {d, c, b, a}; //赋值
wire [3:0] in_vec = {d, c, b, a}; //声明+赋值由于 verilog 是一种弱类型(Loosely Typed Language)语言,所以也可以使用两位地址信号,就好像它是一个integer类型一样,然后该信号将被用作确定选择4个元素中的哪一个的指针。
下面的代码片段展示了如何实现这种方法。由于多路选择器的输出是wire类型,所以必须在这种情况下使用连续赋值。
assign mux_out = in_vec[addr];📣您有任何问题,都可以在评论区和我交流📃!
📣本文由 孤独的单刀 原创,首发于CSDN平台🐵,博客主页:wuzhikai.blog.csdn.net
📣您的支持是我持续创作的最大动力!如果本文对您有帮助,还请多多点赞👍、评论💬和收藏⭐!
相关文章:

Verilog实现组合逻辑电路
在verilog 中可以实现的数字电路主要分为两类----组合逻辑电路和时序逻辑电路。组合逻辑电路比较简单,仅由基本逻辑门组成---如与门、或门和非门等。当电路的输入发生变化时,输出几乎(信号在电路中传递时会有一小段延迟)立即就发生…...

2023前端菜鸟笔试血泪史html5-one--找到工作前都更新
1.说说对html语义化的理解 什么的HTML语义化,顾名思义,HTML语义化就是可以不通过了解HTML的内容,就可以知道这个部分所代表的的意义。 HTML语义化的意义:在使用HTML标签构建页面时,避免大篇幅的使用无语义的标签。 …...
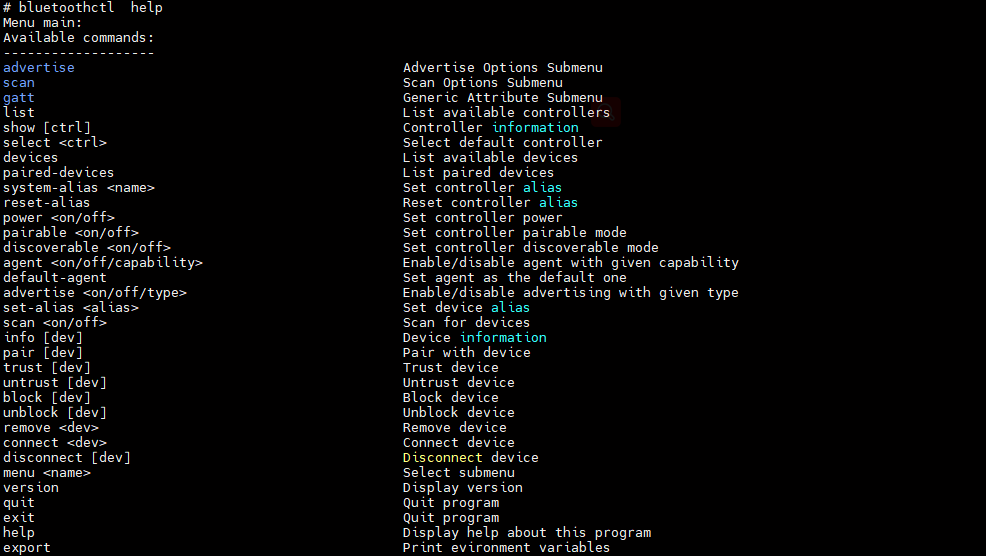
蓝牙调试工具集合汇总
BLE 该部分主要分享一下常用的蓝牙调试工具,方便后续蓝牙抓包及分析。 目录 1 hciconfig 2 hcitool 3 hcidump 4 hciattach 5 btmon 6 bluetoothd 7 bluetoothctl 1 hciconfig 工具介绍:hciconfig,HCI 设备配置工具 命令格式&…...

Java 获取文件后缀名【一文总结所有方法】
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
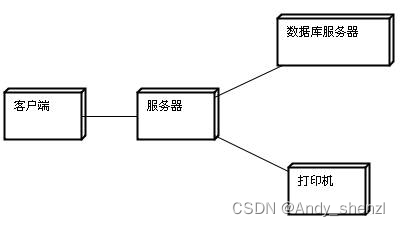
UML常见图的总结
一、概述 UML:Unified Modeling Language,统一建模语言,支持从需求分析开始的软件开发的全过程。是一个支持模型化和软件系统开发的图形化语言、为软件开发的所有阶段提供模型化和可视化支持,包括由需求分析到规格,到…...

WebRTC系列-工具系列之音频相关工具
文章目录 1. audio_util数据格式转换类2. WavFile文件读写类2.1 读取wav文件2.2 写入wav文件这篇文章主要介绍WebRTC中一些音频工具这些,大部分都在 common_audio目录下,这个文件夹下提供音频的大量算法,包括sinc重采样算法,音频数据格式的转换:例如 float转int16_t格式等…...
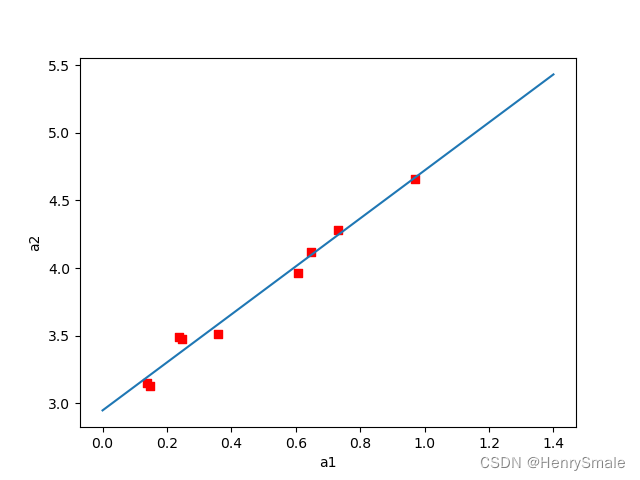
7 线性回归及Python实现
1 统计指标 随机变量XXX的理论平均值称为期望: μE(X)\mu E(X)μE(X)但现实中通常不知道μ\muμ, 因此使用已知样本来获取均值 X‾1n∑i1nXi.\overline{X} \frac{1}{n} \sum_{i 1}^n X_i. Xn1i1∑nXi.方差variance定义为: σ2E(∣X−μ∣2).\sigma^2 E(|…...

适合小团队协作、任务管理、计划和进度跟踪的项目任务管理工具有哪些?
适合小团队协作、任务管理、计划和进度跟踪的项目任务管理工具有哪些? 大家可以参考这个模板:http://s.fanruan.com/irhj8管理项目归根结底在管理人、物,扩展来说便是: 人:员工能力、组织机制; 物:项目内…...

从100%进口到自主可控,从600块降到10块,中科院攻克重要芯片
前言 2月28日,“20多位中科院专家把芯片价格打到10块”冲上微博热搜,据河南省官媒大象新闻报道,热搜中提到的中科院专家所在企业为全球最大的PLC分路器芯片制造商仕佳光子,坐落于河南鹤壁。 为实现芯片技术自主可控自立自强&#…...

关于git的一些基本点总结
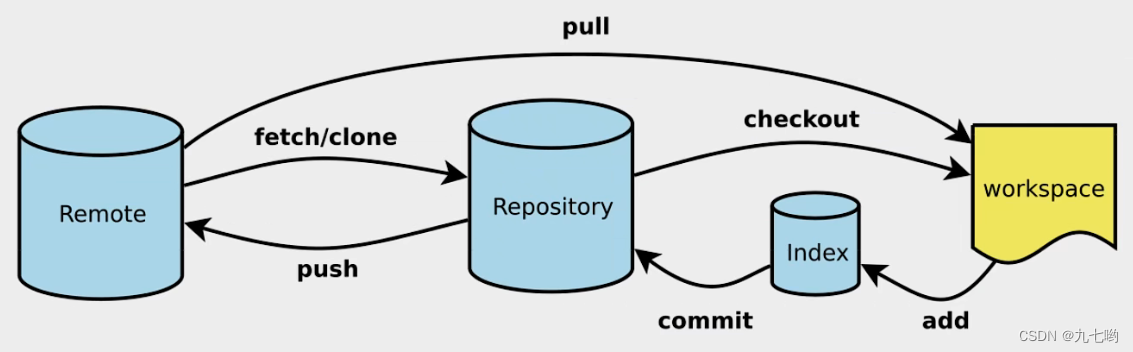
1.什么是git? git是一个常用的分布式版本管理工具。 2.git 的常用命令: clone(克隆): 从远程仓库中克隆代码到本地仓库 checkout (检出):从本地仓库中检出一个仓库分支然后进行修订 add(添加): 在提交前…...
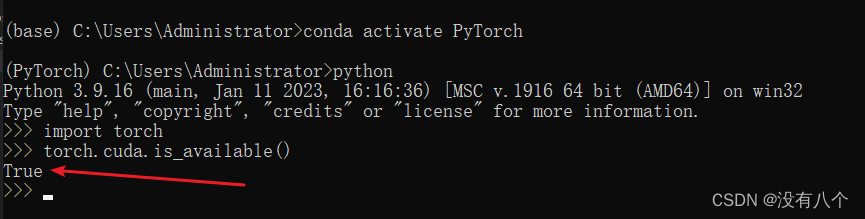
PyTorch保姆级安装教程
1 安装CUDA1.1 查找Nvidia适用的CUDA版本桌面右键,【打开 NVIDIA控制面板】查看【系统信息】查看NVIDIA的支持的CUDA的版本,下图可知支持的版本是 10.11.2 下载CUDACUDA下载官方网址https://developer.nvidia.com/cuda-toolkit-archive找到适合的版本下载…...
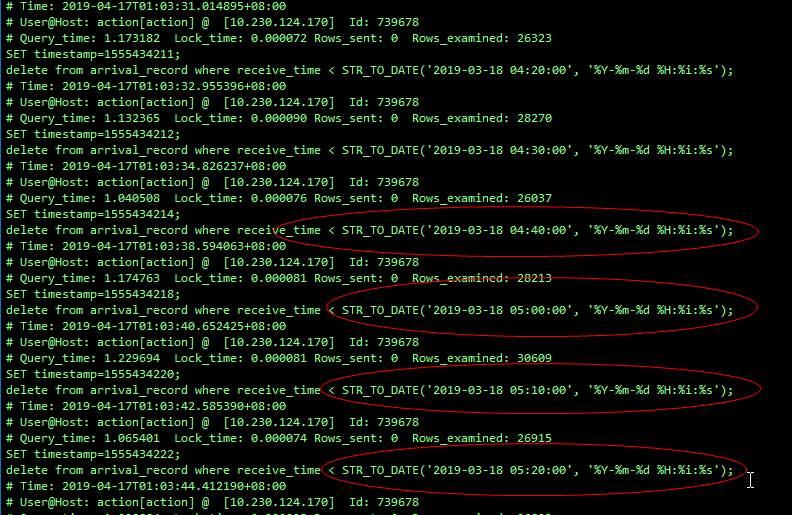
MySQL 上亿大表如何优化?
背景XX 实例(一主一从)xxx 告警中每天凌晨在报 SLA 报警,该报警的意思是存在一定的主从延迟。(若在此时发生主从切换,需要长时间才可以完成切换,要追延迟来保证主从数据的一致性)XX 实例的慢查询…...
Git(狂神课堂笔记)
1.首先去git官网下载我们对应的版本Git - Downloading Package (git-scm.com) 2.安装后我们会发现git文件夹里有三个应用程序: Git Bash:Unix与Linux风格的命令行,使用最多,推荐最多 Git CMD:Windows风格的命令行 G…...

「2」指针进阶,最详细指针和数组难题解题思路
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练 🔥座右铭:“不要等到什么都没有了,才下定决心去做” 🚀🚀🚀大家觉不错…...

云服务器是做什么的?云服务器典型的应用场景介绍
云服务器可能是很多企业以及个人上云用户的必选产品了,但是对于初学者或者非专业的用户来说云服务器还是比较陌生的,它到底是干什么的,如此生活中哪些地方可以接触到,这篇文章将详细的介绍云服务器使用的应用场景以及相关的操作 本…...
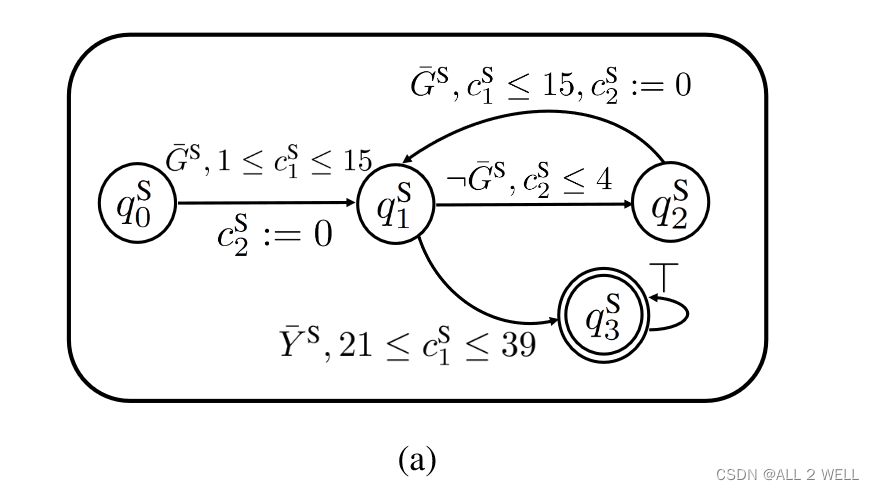
【论文随笔】Transfer of temporal logic formulas in reinforcement learning
Zhe Xu and Ufuk Topcu. 2019. Transfer of temporal logic formulas in reinforcement learning. In Proceedings of the 28th International Joint Conference on Artificial Intelligence (IJCAI’19). AAAI Press, 4010–4018. 这是一篇将inference和learning结合起来的文章…...

蓝桥杯-货物摆放
蓝桥杯-货物摆放1、题目描述1.1 答案提交1.2 运行限制2、解决方案2.1 方案一:暴力解法(三重循环)2.2 方案二:找出乘机的因子1、题目描述 小蓝有一个超大的仓库,可以摆放很多货物。 现在,小蓝有 n 箱货物要摆放在仓库,每…...

10 种顶流聚类算法 Python 实现(附完整代码)
聚类或聚类分析是无监督学习问题。它通常被用作数据分析技术,用于发现数据中的有趣模式,例如基于其行为的客户群。 有许多聚类算法可供选择,对于所有情况,没有单一的最佳聚类算法。相反,最好探索一系列聚类算法以及每…...

微信小程序第一节 —— 自定义顶部、底部导航栏以及获取胶囊体位置信息。
一、前言 大家好!我是 是江迪呀。我们在进行微信小程序开发时,常常需要自定义一些东西,比如自定义顶部导航、自定义底部导航等等。那么知道这些自定义内容的具体位置、以及如何适配不同的机型就变得尤为重要。下面让我以在iPhone机型&#x…...
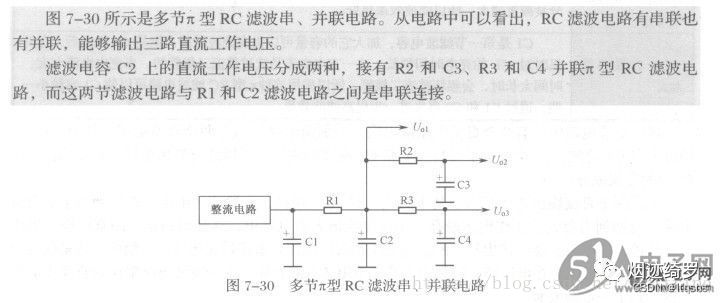
快速吃透π型滤波电路-LC-RC滤波器
π型滤波器简介 π型滤波器包括两个电容器和一个电感器,它的输入和输出都呈低阻抗。π型滤波有RC和LC两种, 在输出电流不大的情况下用RC,R的取值不能太大,一般几个至几十欧姆,其优点是成本低。其缺点是电阻要消耗一些…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...
