蓝桥杯-货物摆放
蓝桥杯-货物摆放
- 1、题目描述
- 1.1 答案提交
- 1.2 运行限制
- 2、解决方案
- 2.1 方案一:暴力解法(三重循环)
- 2.2 方案二:找出乘机的因子
1、题目描述
小蓝有一个超大的仓库,可以摆放很多货物。
现在,小蓝有 n 箱货物要摆放在仓库,每箱货物都是规则的正方体。小蓝规定了长、宽、高三个互相垂直的方向,每箱货物的边都必须严格平行于长、宽、高。
小蓝希望所有的货物最终摆成一个大的长方体。即在长、宽、高的方向上分别堆 L、W、H 的货物,满足n=L×W×H。
给定 n,请问有多少种堆放货物的方案满足要求。
例如,当 n=4 时,有以下 66 种方案:1×1×4、1×2×2、1×4×1、2×1×2、2×2×1、4×1×1、1×1×4、1×2×2、1×4×1、2×1×2、2×2×1、4×1×1。
请问,当 n=2021041820210418 (注意有 1616 位数字)时,总共有多少种方案?
提示:建议使用计算机编程解决问题。
1.1 答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
1.2 运行限制
- 最大运行时间:1s
- 最大运行内存: 256M
2、解决方案
2.1 方案一:暴力解法(三重循环)
long num = 2021041820210418l;int count = 0;for ( long i = 1 ; i < num ; i++ ){for ( long j = 1 ; j < num ; j++ ){for ( long k = 1 ; k < num ; k++ ){if ( i * j *um ){count++;}}}}
这个明显超时了
2.2 方案二:找出乘机的因子
我们先找出能够被num整除的所有因子,找到这些因子之后,由于是三个因子相乘的积等于num,由于因子的数量比num小太多了,此时对所有因子进行三重循环统计三个因子乘积=num的数量即可。
package LanQiaoBei.货物摆放;import java.util.HashSet;public class Main {//直接三重循环时间复杂度非常大,另辟蹊径public static void main(String[] args) {long num = 2021041820210418L;//用HashSet存放num因子,自动解决因子重复问题HashSet<Long> common = new HashSet<>();//遍历到num的平方根技术,不需要都遍历一遍for (long i = 1; i <= Math.sqrt(num); i++) {if (num % i == 0) {common.add(i);//可以整除就加入集合//i可以被整除,求出num的另外一个除数long n = num / i;if (n != i) { //不加判断也行,因为我们用的hashset,但是系统判定超时common.add(n);}}}System.out.println("common.size():" + common.size());System.out.println(common);long count = 0;//这里不需要三重循环,前两个数确定后,第三个数也就确定了for (Long i : common) {for (Long j : common) {long k = num / (i * j);if (i * j * k == num) {count++;}}}System.out.println(count);}}
运行结果如下图:

相关文章:

蓝桥杯-货物摆放
蓝桥杯-货物摆放1、题目描述1.1 答案提交1.2 运行限制2、解决方案2.1 方案一:暴力解法(三重循环)2.2 方案二:找出乘机的因子1、题目描述 小蓝有一个超大的仓库,可以摆放很多货物。 现在,小蓝有 n 箱货物要摆放在仓库,每…...

10 种顶流聚类算法 Python 实现(附完整代码)
聚类或聚类分析是无监督学习问题。它通常被用作数据分析技术,用于发现数据中的有趣模式,例如基于其行为的客户群。 有许多聚类算法可供选择,对于所有情况,没有单一的最佳聚类算法。相反,最好探索一系列聚类算法以及每…...

微信小程序第一节 —— 自定义顶部、底部导航栏以及获取胶囊体位置信息。
一、前言 大家好!我是 是江迪呀。我们在进行微信小程序开发时,常常需要自定义一些东西,比如自定义顶部导航、自定义底部导航等等。那么知道这些自定义内容的具体位置、以及如何适配不同的机型就变得尤为重要。下面让我以在iPhone机型&#x…...
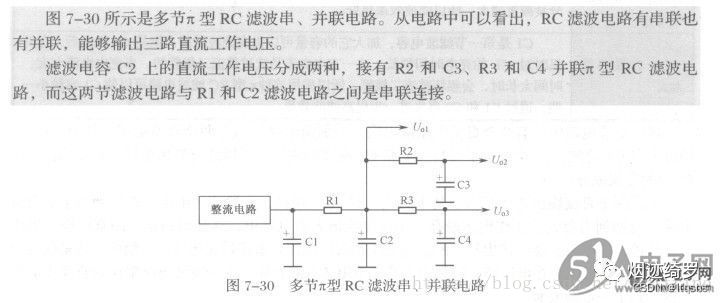
快速吃透π型滤波电路-LC-RC滤波器
π型滤波器简介 π型滤波器包括两个电容器和一个电感器,它的输入和输出都呈低阻抗。π型滤波有RC和LC两种, 在输出电流不大的情况下用RC,R的取值不能太大,一般几个至几十欧姆,其优点是成本低。其缺点是电阻要消耗一些…...
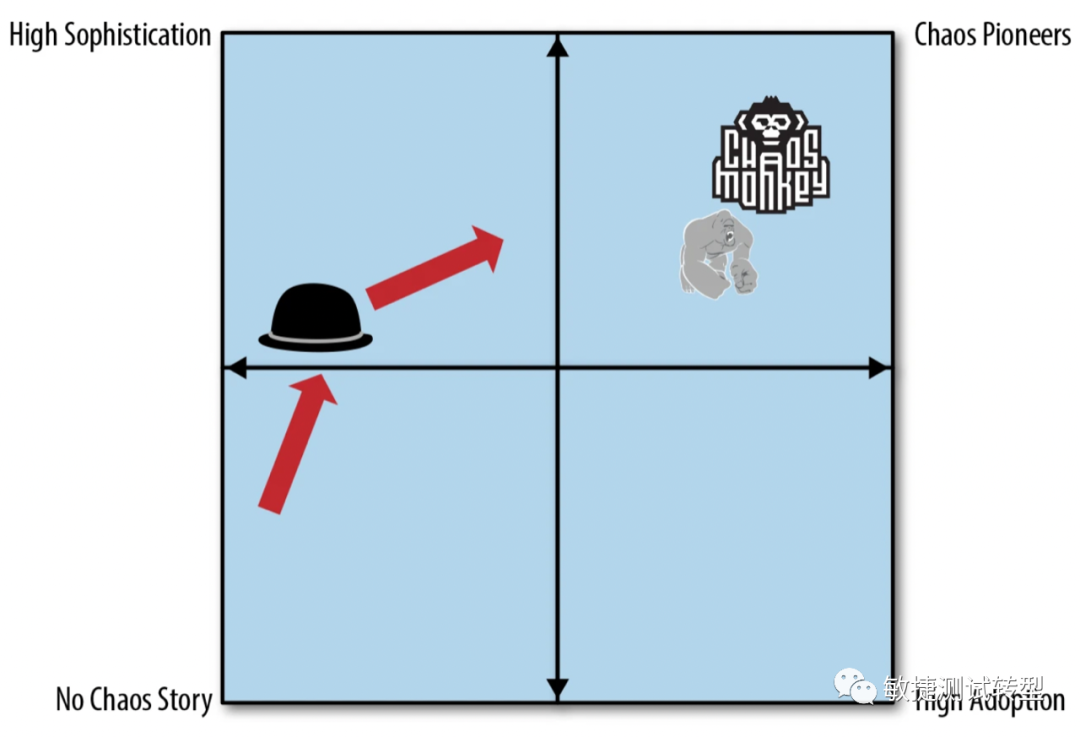
聊聊混沌工程
这是鼎叔的第五十四篇原创文章。行业大牛和刚毕业的小白,都可以进来聊聊。欢迎关注本专栏和微信公众号《敏捷测试转型》,大量原创思考文章陆续推出。混沌工程是一门新兴学科,它不仅仅只是个技术活动,还包含如何设计能够持续协作的…...

做为骨干网络的分类模型的预训代码安装配置简单记录
一、安装配置环境 1、准备工作 代码地址 GitHub - bubbliiiing/classification-pytorch: 这是各个主干网络分类模型的源码,可以用于训练自己的分类模型。 # 创建环境 conda create -n ptorch1_2_0 python3.6 # 然后启动 conda install pytorch1.2.0 torchvision…...

网络协议(九):应用层(域名、DNS、DHCP)
网络协议系列文章 网络协议(一):基本概念、计算机之间的连接方式 网络协议(二):MAC地址、IP地址、子网掩码、子网和超网 网络协议(三):路由器原理及数据包传输过程 网络协议(四):网络分类、ISP、上网方式、公网私网、NAT 网络…...
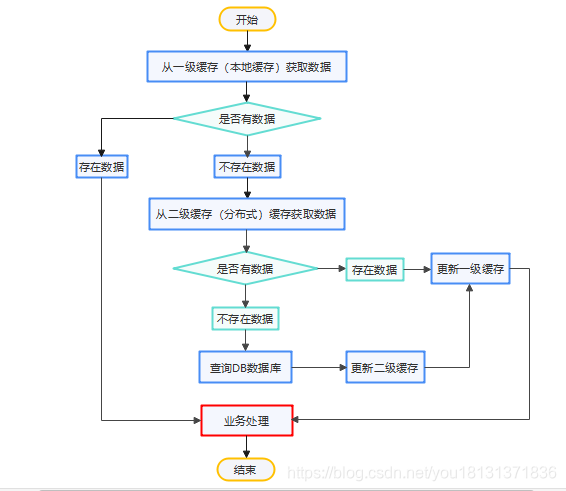
有趣的小知识(三)提升网站速度的秘诀:掌握缓存基础,让你的网站秒开
像MySql等传统的关系型数据库已经不能适用于所有的业务场景,比如电商系统的秒杀场景,APP首页的访问流量高峰场景,很容易造成关系型数据库的瘫痪,随着缓存技术的出现很好的解决了这个问题。 一、缓存的概念(什么是缓存…...

SpringCloud之服务拆分和实现远程调用案例
服务拆分对单体架构项目来说:简单方便,高度耦合,扩展性差,适合小型项目。而对于分布式架构来说:低耦合,扩展性好,但架构复杂,难度大。微服务就是一种良好的分布式架构方案࿱…...
: com.atguigu.dao.UserDao.save)
mybatis: Invalid bound statement (not found): com.atguigu.dao.UserDao.save
问题描述: 1 问题实质: dao层(又叫mapper接口)跟mapper.xml文件没有映射 2 问题原因: 出现这种映射问题的原因分为低级原因和更低级原因两种 更低级原因: (1)dao层的方法和mapper.xml中的方法不一样; (2)mapper中的namespace 值 和对应的dao层entity层不一致 &…...
JavaScript 代码规范
所有的 JavaScript 项目适用同一种规范。JavaScript 代码规范代码规范通常包括以下几个方面:变量和函数的命名规则空格,缩进,注释的使用规则。其他常用规范……规范的代码可以更易于阅读与维护。代码规范一般在开发前规定,可以跟你的团队成员…...

6综合项目 旅游网 【6.我的收藏和收藏排行榜】
我的收藏分析先登录→拿到当前登录的用户信息,从数据库中获取uid和对应uid的rid集合→将rid集合信息展示到我的收藏前台代码判断用户是否登录,传递uid,通过uid查找其对应的rid集合当查询的属性涉及到多张表,则必须使用多表连接&am…...
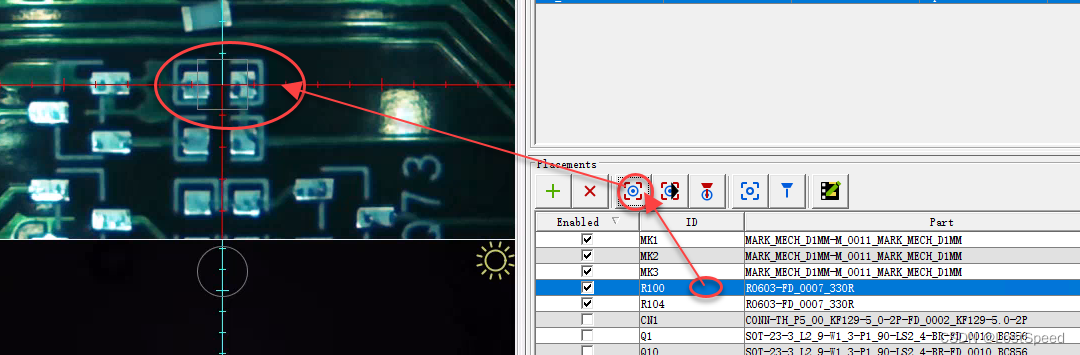
openpnp - error - 微调mark点坐标后,更新板子其他原件其他坐标报错的变通方法
文章目录openpnp - error - 微调mark点坐标后,更新板子其他原件其他坐标报错的变通方法概述想出来一个变通的方法ENDopenpnp - error - 微调mark点坐标后,更新板子其他原件其他坐标报错的变通方法 概述 载入坐标文件后, 指定左下角远点坐标, 然后定位板子上的3个Mark点, 因为…...

借助ChatGPT爆火,股价暴涨又暴跌后,C3.ai仍面临巨大风险
来源:猛兽财经 作者:猛兽财经 C3.ai的股价 作为一家人工智能技术提供商,C3.ai(AI)的股价曾在2021年初随着炒作情绪的增加,达到了历史最高点,但自那以后其股价就下跌了90%,而且炒作情…...

蓝桥杯-数位排序
蓝桥杯-数位排序1、问题描述2、解题思路3、代码实现1、问题描述 小蓝对一个数的数位之和很感兴趣, 今天他要按照数位之和给数排序。当 两个数各个数位之和不同时, 将数位和较小的排在前面, 当数位之和相等时, 将数值小的排在前面。 例如, 2022 排在 409 前面, 因为 2022 的数位…...
)
【ES实战】ES 插件包离线安装(本地文件)
ES 插件包离线安装(本地文件) 文章目录ES 插件包离线安装(本地文件)使用安装命令安装直接解压式验证安装情况常用的分词插件analysis-ik analysis-pinyin analysis-dynamic-synonym 在集群的节点上分发插件的ZIP安装包 使用安…...

Spring的核心基础——IOC与DI
文章目录一、Spring简介1 Spring介绍1.1 为什么要学1.2 学什么2 初识Spring2.1 Spring家族2.2 Spring发展史3 Spring体系结构3.1 Spring Framework系统架构图4 Spring核心概念问题导入4.1 核心概念二、IOC和DI入门1 IOC入门问题导入1.1 门案例思路分析1.2 实现步骤1.3 实现代码…...

C++正则表达式基础
文章目录1. 查找第一个匹配的2. 查找所有结果3. 打印匹配结果的上下文4. 使用子表达式5. 查找并替换注意: .(点)在括号中没有特殊含义,无需转义用\转义。 1. 查找第一个匹配的 #include <iostream> #include <regex>using names…...

如何在网络安全中使用人工智能并避免受困于此
人工智能在网络安全中的应用正在迅速增长,并对威胁检测、事件响应、欺诈检测和漏洞管理产生了重大影响。根据Juniper Research的一份报告,预计到2023年,使用人工智能进行欺诈检测和预防将为企业每年节省110亿美元。但是,如何将人工…...

生态 | 人大金仓与超聚变的多个产品完成兼容认证
近日,人大金仓与超聚变数字技术有限公司(简称“超聚变”)完成了多款产品的兼容互认测试。测试表明,人大金仓KingbaseES V8数据库与超聚变服务器操作系统FusionOS、超聚变FusionOne基础设施完全兼容,人大金仓异构数据同…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...
