TikTok真题第4天 | 1366. 通过投票对团队排名、1029.两地调度、562.矩阵中最长的连续1线段
1366. 通过投票对团队排名
题目链接:rank-teams-by-votes/
解法:
这道题就是统计每个队伍在每个排名的投票数,队伍为A、B、C,则排名有1、2、3,按照投票数进行降序排列。如果有队伍在每个排名的投票数都一样,那么按照字母序进行排列。
可以用哈希表也可以用数组处理(因为最多有26个队伍,即26个字母)。
细节在于按照字母序排列,为了统一为按照数字降序排列,可以把队伍(字母)转为 (Z - 队伍),这样的话,如果队伍是A,那么数字为26,字母为Z,那么数字为0,字母序排列=数字降序排列。
参考题解:1.使用哈希表排序
2.数组+把字母转为数字
边界条件:无
时间复杂度:O(nk+n*nlogn),其中 n 是数组 votes中每一个字符串的长度(参与排名的人数),k 是数组 votes 的长度(参与投票的人数)。「遍历统计」的时间复杂度为 O(nk),「排序」的时间复杂度为 O(nlogn),由于需要两两比较,那么再乘以n。
空间复杂度:O(n*n)。哈希映射中键值对的数量为 n,每个值使用 O(n) 的空间。
class Solution {
public:string rankTeams(vector<string>& votes) {unordered_map<char, vector<int>> ranking;// 初始化map,key是字母(队),value是所有排名的投票数// 为了最后一个排序规则:按照字母序来排,所以value加了一个元素for (char v: votes[0]) {int topn = votes[0].size();ranking[v].resize(topn+1);// 如果v是A,那么最后一位是26,如果是Z,那么为0ranking[v][topn] = 'Z' - v;}//遍历统计每个队伍每个排名的票数for (const string& vote: votes) {for (int i=0; i<vote.size(); i++) {ranking[vote[i]][i]++;}}// 复制到可排序的容器中vector<pair<char, vector<int>>> sortedRanking(ranking.begin(), ranking.end());// 排序,排名相等的情况下按字母序来排sort(sortedRanking.begin(), sortedRanking.end(), [](const auto& s1, const auto& s2) {return s1.second > s2.second;});string res;for (auto& rank: sortedRanking) {res += rank.first;}return res;}
};1029.两地调度
题目链接:two-city-scheduling/
解法:
假定2N人都去B市,则费用为 price_B累加:sum_b。现在让其中的N个人不去B市,而是直接去A市。如果其中一个去A市,那么这个费用就变成 sum_b + (price_A - price_B)。
所有的price_B累加是固定值,要让sum最小,我们只要按(price_A - price_B)排序,这个值小的前N个人去A市,那sum就最小。
参考解法:贪心
边界条件:无
时间复杂度:O(nlogn),排序。
空间复杂度:O(n)
class Solution {
public:int twoCitySchedCost(vector<vector<int>>& costs) {sort(costs.begin(), costs.end(), [] (const vector<int>& c1, const vector<int>& c2) {return (c1[0] - c1[1]) < (c2[0] - c2[1]);});int result = 0;int n = costs.size() / 2;for (int i=0; i<n; i++) {result += costs[i][0] + costs[n+i][1];};return result;}
};562.矩阵中最长的连续1线段
题目链接:longest-line-of-consecutive-one-in-matrix
解法:
思路参考:yiduobo的每日leetcode 562.矩阵中最长的连续1线段 - 知乎
动态规划问题。令row[i][j]、col[i][j]、left[i][j]、right[i][j]分别表示以单元格(i, j)为终点的水平方向、竖直方向、左对角线方向、右对角线方向上的连续1的数目,那么对于这四个值,若当前的mat[i][j] = 0,这四个值都都为0,否则:
当j = 0时,row[i][j] = 1,否则row[i][j] = row[i][j -1] + 1
当i = 0时,col[i][j] = 1,否则col[i][j] = col[i - 1][j] + 1
当i = 0或j = 0时,left[i][j] = 0,否则left[i][j] = left[i - 1][j - 1] + 1
当i = 0或j = n - 1时,right[i][j] = 0,否则right[i][j] = left[i - 1][j + 1] + 1
计算完成后,取四个数组中的最大值作为答案即可。
这个题涉及到4个方向,初始化比较麻烦,所以没有初始化,直接从0开始遍历。
具体代码实现参考:动态规划
边界条件:无
时间复杂度:O(mn)
空间复杂度:O(mn)
class Solution {
public:int longestLine(vector<vector<int>>& mat) {int m = mat.size();int n = mat[0].size();int res = 0;vector<vector<vector<int>>> dp(4, vector<vector<int>>(m, vector<int>(n, 0)));for (int i=0; i<m; i++) {for (int j=0; j<n; j++) {if (mat[i][j] == 0) continue;dp[0][i][j] = j==0? 1: 1+dp[0][i][j-1];dp[1][i][j] = i==0? 1: 1+dp[1][i-1][j];dp[2][i][j] = (i==0 || j==0)? 1: 1+dp[2][i-1][j-1];dp[3][i][j] = (i==0 || j==n-1)? 1: 1+dp[3][i-1][j+1]; // 更新结果 for (int k=0; k<4; k++) {res = max(res, dp[k][i][j]);}}}return res;}
};相关文章:

TikTok真题第4天 | 1366. 通过投票对团队排名、1029.两地调度、562.矩阵中最长的连续1线段
1366. 通过投票对团队排名 题目链接:rank-teams-by-votes/ 解法: 这道题就是统计每个队伍在每个排名的投票数,队伍为A、B、C,则排名有1、2、3,按照投票数进行降序排列。如果有队伍在每个排名的投票数都一样…...

时序预测 | Matlab实现SSA-CNN-LSTM麻雀算法优化卷积长短期记忆神经网络时间序列预测
时序预测 | Matlab实现SSA-CNN-LSTM麻雀算法优化卷积长短期记忆神经网络时间序列预测 目录 时序预测 | Matlab实现SSA-CNN-LSTM麻雀算法优化卷积长短期记忆神经网络时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 MATLAB实现SSA-CNN-LSTM麻雀算法优化卷积长短…...
负载均衡——Ribbon
文章目录 Ribbon和Eureka配合使用项目引入RibbonRestTemplate添加LoadBalanced注解注意自定义均衡方式代码注册方式配置方式 Ribbon脱离Eureka使用 Ribbon,Nexflix发布的负载均衡器,有助于控制HTTP和TCP客户端的行为。基于某种负载均衡算法(轮…...

7.微服务设计原则
1.微服务演进策略 从单体应用向微服务演进策略: 绞杀者策略,修缮者策略的另起炉灶策略; 绞杀者策赂 绞杀者策略是一种逐步剥离业务能力,用微服务逐步替代原有单体应用的策略。它对单体应用进行领域建模,根据领域边界࿰…...

【MATLAB库函数系列】线性调频Z(Chirp-Z,CZT)的MATLAB源码和C语言实现
在上一篇博客 【数字信号处理】线性调频Z(Chirp-Z,CZT)算法详解 已经详细介绍了CZT变换的应用背景和原理,先回顾一下: 回顾CZT算法 采用 FFT 算法可以很快计算出全部 N N N点 DFT 值,即Z变换 X ( z ) X(z) <...
BIT-6-指针(C语言初阶学习)
1. 指针是什么 2. 指针和指针类型 3. 野指针 4. 指针运算 5. 指针和数组 6. 二级指针 7. 指针数组 1. 指针是什么? 指针是什么? 指针理解的2个要点: 指针是内存中一个最小单元的编号,也就是地址平时口语中说的指针,通常…...
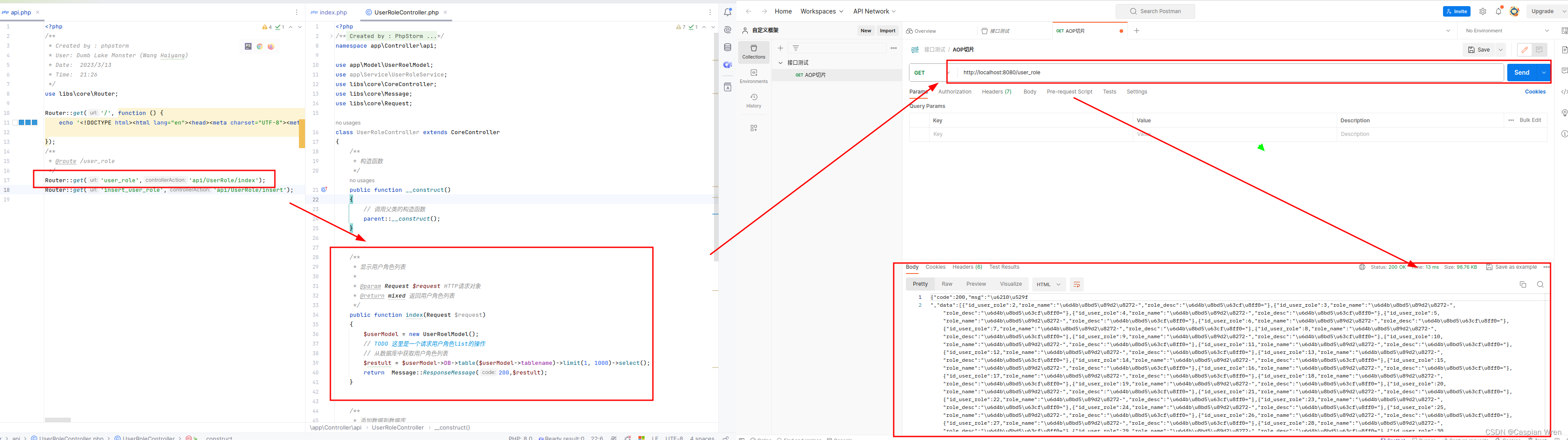
傻瓜式教学Docker 使用docker compose部署 php nginx mysql
首先你可以准备这个三个服务,也可以在docker compose 文件中 直接拉去指定镜像,这里演示的是镜像服务已经在本地安装好了,提供如下: PHP # 设置基础镜像 FROM php:8.2-fpm# install dependencies RUN apt-get update && apt-get install -y \vim \libzip-dev \libpng…...

node express简单微服务
首先,安装所需的依赖项,可以使用npm或yarn进行安装: $ npm install express axios接下来,创建一个名为service1.js的文件,用于实现第一个微服务: const express require(express); const axios require…...
nginx-proxy-manager初次登录502 bad gateway
nginx-proxy-manager初次登录502 bad gateway 按照官方docker-compose安装后,页面如下: 默认账户密码: adminexample.com/changeme点击sign in,提示Bad Gateway 打开调试 重装后依然如此,最后查阅githup issue 找到答案 https://github.com/NginxProxyManager/nginx-proxy-…...

Servlet见解2
4 创建servlet的三种方式 4.1 实现Servlet接口的方式 import javax.servlet.*; import javax.servlet.annotation.WebServlet; import java.io.IOException;WebServlet("/test1") public class Servlet1 implements Servlet {Overridepublic void init(ServletConf…...

【SpringCloud】-OpenFeign实战及源码解析、与Ribbon结合
一、背景介绍 二、正文 OpenFeign是什么? OpenFeign(简称Feign)是一个声明式的Web服务客户端,用于简化服务之间的HTTP通信。与Nacos和Ribbon等组件协同,以支持在微服务体系结构中方便地进行服务间的通信;…...

走进数字金融峰会,为金融科技数字化赋能
12月20—21日,FSIDigital数字金融峰会在上海圆满召开。本次峰会包含InsurDigital数字保险峰会和B&SDigital数字银行与证券峰会2场平行峰会;吸引了近600位来自保险、银行、证券以及金融科技等行业的领导者和专家齐聚一堂,共同探讨金融业数…...

docker-compose部署kafka
docker-compose.yml配置 version: "3" services:kafka:image: bitnami/kafka:latestports:- 7050:7050environment:- KAFKA_ENABLE_KRAFTyes- KAFKA_CFG_PROCESS_ROLESbroker,controller- KAFKA_CFG_CONTROLLER_LISTENER_NAMESCONTROLLER- KAFKA_CFG_LISTENERSPLAIN…...
Spark与Hadoop的关系和区别
在大数据领域,Spark和Hadoop是两个备受欢迎的分布式数据处理框架,它们在处理大规模数据时都具有重要作用。本文将深入探讨Spark与Hadoop之间的关系和区别,以帮助大家的功能和用途。 Spark和Hadoop简介 1 Hadoop Hadoop是一个由Apache基金会…...
蓝桥杯-Excel地址[Java]
目录: 学习目标: 学习内容: 学习时间: 题目: 题目描述: 输入描述: 输出描述: 输入输出样例: 示例 1: 运行限制: 题解: 思路: 学习目标: 刷蓝桥杯题库日记 学习内容: 编号96题目Ex…...

OSPF多区域配置-新版(12)
目录 整体拓扑 操作步骤 1.基本配置 1.1 配置R1的IP 1.2 配置R2的IP 1.3 配置R3的IP 1.4 配置R4的IP 1.5 配置R5的IP 1.6 配置R6的IP 1.7 配置PC-1的IP地址 1.8 配置PC-2的IP地址 1.9 配置PC-3的IP地址 1.10 配置PC-4的IP地址 1.11 检测R5与PC1连通性 1.12 检测…...
华为---USG6000V防火墙web基本配置示例
目录 1. 实验要求 2. 配置思路 3. 网络拓扑图 4. USG6000V防火墙端口和各终端相关配置 5. 在USG6000V防火墙web管理界面创建区域和添加相应端口 6. 给USG6000V防火墙端口配置IP地址 7. 配置通行策略 8. 测试验证 8.1 逐个删除策略,再看各区域终端通信情况 …...
Ksher H5页面支付实例指导 (PHP实现)
背景 前两天,公司的项目,为了满足泰国客户的支付需求,要求使用 Ksher (开时支付) 对接任务突然就给了鄙人,一脸懵 … 通过了解客户的使用场景、以及参考官网指导 发现:Ksher支付最令人满意的便是 —— 提供了便捷的 支…...
https密钥认证、上传镜像实验
一、第一台主机通过https密钥对认证 1、安装docker服务 (1)安装环境依赖包 yum -y install yum-utils device-mapper-persistent-data lvm2 (2)设置阿里云镜像源 yum-config-manager --add-repo http://mirrors.aliyun.com/do…...

three.js使用精灵模型Sprite渲染森林
效果: 源码: <template><div><el-container><el-main><div class"box-card-left"><div id"threejs" style"border: 1px solid red"></div><div class"box-right&quo…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...
