算法时间空间复杂度计算—空间复杂度
算法时间空间复杂度计算—空间复杂度
- 空间复杂度定义
- 影响空间复杂度的因素
- 算法在运行过程中临时占用的存储空间讲解
- 计算方法
- 例子
- 1、空间算法的常数阶
- 2、空间算法的线性阶(递归算法)
- 3、二分查找分析
- 方法一(迭代法)
- 方法二(递归法)
- 4、斐波那契数列
- 方法一(迭代法)
- 方法二(递归法)
空间复杂度定义
空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度。
一个算法在计算机存储器上所占用的存储空间,包括程序代码所占用的空间,输入数据所占用的空间和辅助变量所占用的空间这三个方面。
影响空间复杂度的因素

注意:
一个算法的空间复杂度只考虑在运行过程中为局部变量分配的存储空间的大小,它包括为参数表中形参变 量分配的存储空间和为在函数体中定义的局部变量分配的存储空间两个部分。若一个算法为递归算法,其空间复杂度为递归所使用的堆栈空间的大小。它等于一次调用所分配的临时存储空间的大小乘以被调用的次数(即为递归调用的次数加1,这个1表示开始进行的一次非递归调用)
递归的空间复杂度: 每次递归所开空间*深度。
算法在运行过程中临时占用的存储空间讲解
1、有的算法只需要占用少量的临时工作单元,而且不随问题规模的大小而改变,我们称这种算法是“就地”进行的,是节省存储的算法,下面会介绍。
2、有的算法需要占用的临时工作单元数与解决问题的规模n有关,它随着n的增大而增大,当n较大时,将占用较多的存储单元,例如快速排序和归并排序算法就属于这种情况。
计算方法
①忽略常数,用O(1)表示
②递归算法的空间复杂度=递归深度n*每次递归所要的辅助空间
③对于单线程来说,递归有运行时堆栈,求的是递归最深的那一次压栈所耗费的空间的个数,因为递归最深的那一次所耗费的空间足以容纳它所有递归过程。
例子
1、空间算法的常数阶
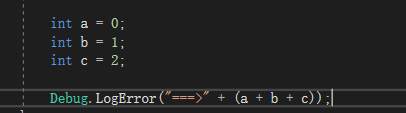
如上图,这里有三个局部变量分配了存储空间,所以f(n) = 1 + 1 + 1 = 3,根据上面的法则该函数不受n的影响且为常数项,所以空间复杂度记作O(1)。这种与问题的大小无关(n的多少),执行时间恒定的算法,我们称之为具有O(1)的空间复杂度,又叫常数阶。
2、空间算法的线性阶(递归算法)
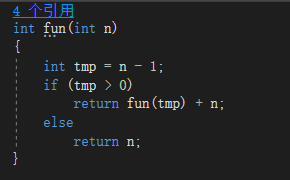
如上图,这是一个递归算法(计算从n + (n-1) + (n-2) + … + 2 + 1的和)
每当执行一次该函数就会为tmp分配一个临时存储空间,所以f(n) = 1*(n-1+1) = n,函数是受n影响的所以空间复杂度记为O(n)。
3、二分查找分析
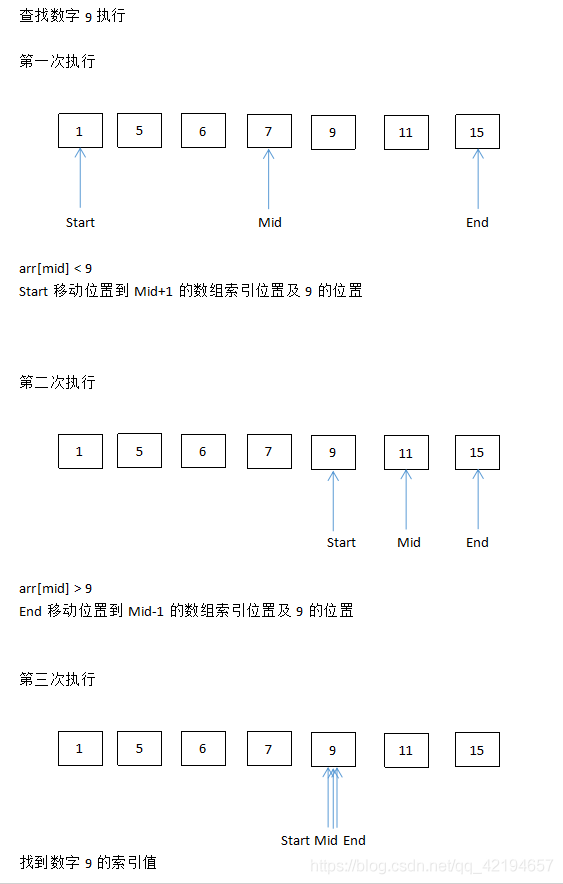
方法一(迭代法)
/// <summary>/// 二分查找/// </summary>/// <param name="arr">查找数组</param>/// <param name="len">数组长度</param>/// <param name="num">查找项</param>/// <returns></returns>int BinarySearch(int[] arr,int len,int num){int left = 0;int right = len - 1;int mid;while (left <= right){mid = (left + right) / 2;if (arr[mid] > num)right = mid - 1;else if (arr[mid] < num)left = mid + 1;elsereturn mid;}return -1;}
时间复杂度:
left、right、mid运算次数
f(n1) = 1 + 1 + 1 = 3
我们将While循环中的运算作为一个整体看待,每次都是折半运算次数
f(n2) = log2^n
总运行次数
f(all) = f(n1)+f(n2) = 3 + log2 ^ n
时间复杂度记为:O(log2^n)
空间复杂度:
算法中left、right、mid只创建的次数
s(n) = 1 + 1 + 1 = 3
空间复杂度记为:O(1)
方法二(递归法)
/// <summary>/// 二分查找(递归法)/// </summary>/// <param name="arr"></param>/// <param name="left"></param>/// <param name="right"></param>/// <param name="num"></param>/// <returns></returns>int BinarySearchRecursion(int[] arr,int left,int right,int num){int mid = (left + right) / 2;if (left <= right){if (arr[mid] > num) {right = mid - 1;return BinarySearchRecursion(arr,left,right,num);}else if (arr[mid] < num){left = mid + 1;return BinarySearchRecursion(arr,left,right,num);}elsereturn mid;}else{return -1;}}
时间复杂度:
运行次数 f(n) = log2 ^ n
时间复杂度记为:O(log2^n)
空间复杂度:
因为整个算法中mid只创建的次数
s(n) = log2 ^ n
空间复杂度记为:O(log2 ^ n)
4、斐波那契数列
斐波那契数列(Fibonacci sequence),又称黄金分割数列、因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……
这个数列从第3项开始,每一项都等于前两项之和。
如果设F(n)为该数列的第n项(n∈N*),那么这句话可以写成如下形式::F(n)=F(n-1)+F(n-2)
显然这是一个线性的递推数列。
通项公式 :
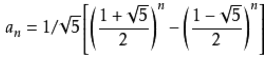
上面就是斐波那契数列的递推公式,这样一个完全是自然数的数列,通项公式却是用无理数来表达的。而且当n趋向于无穷大时,前一项与后一项的比值越来越逼近黄金分割0.618
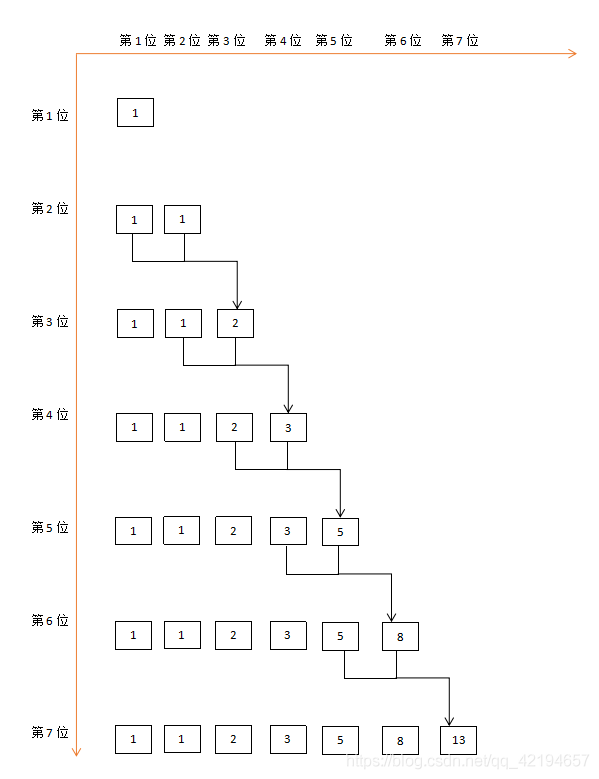
递推是公式是求解斐波那契数列的一个方法,我们当然也可以用计算机编写程序来求解。
方法一(迭代法)
/// <summary>/// 斐波那契(迭代法)/// </summary>/// <param name="n"></param>/// <returns></returns>int Fibonacci(int n){if (n <= 0)return -1;if (n == 1 || n == 2)return 1;else{int num = 0;int a = 1;int b = 1;while (n - 2 > 0){num = a + b;a = b;b = num;n--;}return num;}}
时间复杂度:
while以外的算法语句都忽略不计(不随n的变化而变化)
while算法语句所有语句
f(n) = 4 *(n - 2) = 4n - 8
时间复杂度记为:O(n)
空间复杂度:
算法中num、a、b只创建1次
s(n) = 1 + 1 + 1 = 3
空间复杂度记为:O(1)
方法二(递归法)
/// <summary>/// 斐波那契(递归法)/// </summary>/// <param name="n"></param>/// <returns></returns>int FibonacciRecursion(int n){if (n <= 0)return -1;if (n == 1 || n == 2)return 1;return FibonacciRecursion(n - 1) + FibonacciRecursion(n - 2);}
时间复杂度:
递归调用的形参有两个n - 1 和 n - 2
时间复杂度记为:O(2^n)
空间复杂度:
递归的空间复杂度 =(n + 1)* 调用的深度
空间复杂度记为:O(n)(这里可以简单的根据二叉树的层来进行计算)
相关文章:

算法时间空间复杂度计算—空间复杂度
算法时间空间复杂度计算—空间复杂度 空间复杂度定义影响空间复杂度的因素算法在运行过程中临时占用的存储空间讲解 计算方法例子1、空间算法的常数阶2、空间算法的线性阶(递归算法)3、二分查找分析方法一(迭代法)方法二ÿ…...

计算机专业校招常见面试题目总结
博主面试岗位包括:java开发、软件测试、测试开发等岗位,基于之前经历的面试总结出的一些常见题目。仅供参考,互相学习!! 八股:java开发、测试、测开岗位 Java技术栈:Java基础、JVM、数据结构、…...

网络编程『简易TCP网络程序』
🔭个人主页: 北 海 🛜所属专栏: Linux学习之旅、神奇的网络世界 💻操作环境: CentOS 7.6 阿里云远程服务器 文章目录 🌤️前言🌦️正文TCP网络程序1.字符串回响1.1.核心功能1.2.程序…...
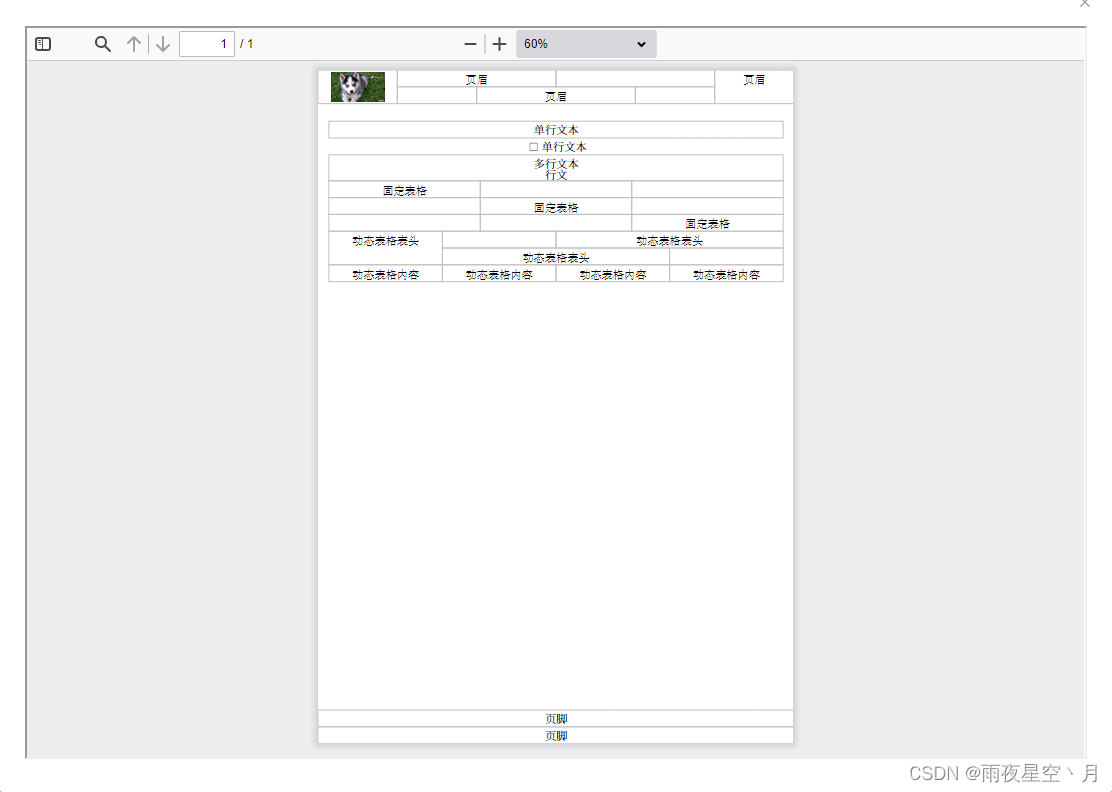
java itext5 生成PDF并填充数据导出
java itext5 生成PDF并填充数据导出 依赖**文本勾选框****页眉**,**页脚****图片**实际图 主要功能有文本勾选框,页眉,页脚,图片等功能。肯定没有专业软件画的好看,只是一点儿方法。仅供参考。 依赖 <!--pdf-->&…...

如何配置TLSv1.2版本的ssl
1、tomcat配置TLSv1.2版本的ssl 如下图所示,打开tomcat\conf\server.xml文件,进行如下配置: 注意:需要将申请的tomcat版本的ssl认证文件,如server.jks存放到tomcat\conf\ssl_file\目录下。 <Connector port"1…...

在CentOS 7上使用普通用户`minio`安装和配置MinIO
指定控制台端口号6901 以下是在CentOS 7上使用普通用户minio安装和配置MinIO的完整步骤,包括设置密码、设置开机自启动,以及使用minio用户启动和关闭服务的过程: 创建MinIO用户: sudo useradd -m minio sudo passwd minio这将创建一个可以登录…...
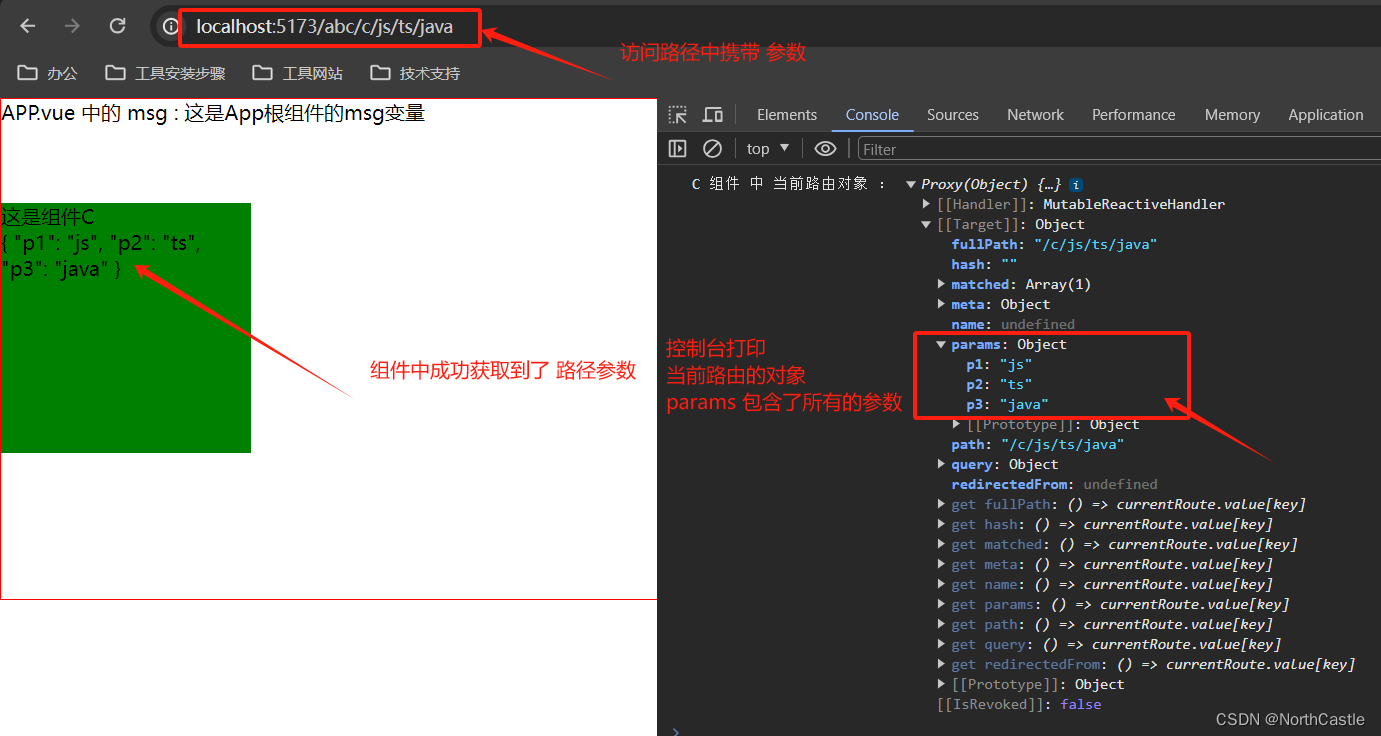
Vue3-27-路由-路径参数的简单使用
什么是路径参数 在路由配置中,可以将【参数】放在【路由路径】中, 从而实现,同一个 路由,同一个组件,因路径参数不同,可以渲染出不同的内容。特点 : 1、当携带不同路径参数的路由相互跳转时&am…...
w7数据库基础之mysql函数
系统函数 1.version() --mysql版本 2.user() --当前登录的数据库用户名system_user() 3.database() --当前使用的数据库名。schema() 4.datadir --数据库路径 5.version_compile_os 操作系统版本,like 后面可以使用%%进行模糊查询。 6.hostname 当前机器…...

智能优化算法应用:基于人工蜂鸟算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于人工蜂鸟算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于人工蜂鸟算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.人工蜂鸟算法4.实验参数设定5.算法结果6.…...

Docker的基础使用
Docker的基础使用 Docker 是一个开放平台,用于开发、运输和运行应用程序。Docker 允许你将应用程序与基础架构分离,从而可以像管理应用程序一样快速交付软件。以下是 Docker 的详细使用指南: 安装 Docker 下载 Docker : 根据你的操作系统…...
、Less的区别与选择 + 基本使用)
Sass(Scss)、Less的区别与选择 + 基本使用
在前端开发中,CSS预处理器成为了提高样式表开发效率的重要工具。Sass(以及其语法Scss)和Less是两个最为流行的CSS预处理器,它们在语法、功能和用法上存在一些差异,因此在选择使用时需要考虑多个因素。 1. Sass 和 Les…...

GPT Zero 是什么?
from https://openaigptguide.com/gptzero/ 在人工智能技术飞速发展的今天,人们对于文字内容的准确性和可信度要求越来越高。例如在学术研究领域,防止抄袭和造假是非常重要的。而对于普通用户而言,辨别哪些内容是由人工智能生成的࿰…...
)
c++学习笔记-提高篇-案例2-员工分组(vector/multimap)
一、案例描述 公司今天招聘10个员工(ABCDEFGHIJ),10名员工进入公司后,需要指派员工在哪个部门工作员工信息:姓名 工资组成;部门分为:策划、美术、研发随机给10名员工分配部门和工作通过multimap进行信息插…...

TrustZone之问答
以下问题有助于测试您的知识。 在Arm架构中,安全状态和物理地址空间分别是什么? 在Arm架构中,安全状态分为安全状态和非安全状态。物理地址空间分为安全物理地址空间和非安全物理地址空间。 在每个异常级别中,是什么确定处理器处于…...

vue3中新增的组合式API:ref、reactive、toRefs、computed、watch、provide/inject、$ref
在 Vue3 中,组合式 API 是一种新的编程模式,它允许你更灵活地组织和重用代码。组合式 API 主要包括以下几个部分: ref:用于创建响应式数据。reactive:用于创建一个响应式对象。toRefs:将一个响应式对象转换…...

Flask 密码重设系统
Flask 密码重设系统【源码来自编程浪子Flask点餐小程序】 web/templates/user/reset_pwd.html {% extends "common/layout_main.html" %} {% block content %} {% include "common/tab_user.html" %} <div class"row m-t user_reset_pwd_wrap&q…...
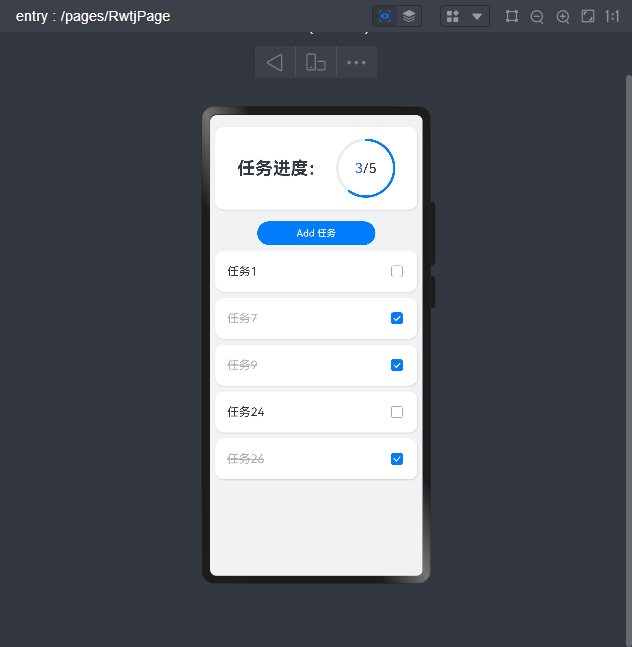
HarmonyOS4.0开发应用(四)【ArkUI状态管理】
ArkUI状态管理 分为以下四个: StateProp和LinkProvide和ConsumeObserved和ObjectLink State 相当于vue中data()内定义的属性变量,相当于react中useState()的使用,即绑定在视图上的响应式变量,可动态更新~ Tip: 标记的变量必须初始化,不可为空…...
)
JS常见正则表达式写法(附案例)
正则表达式方法示例: 1. test方法解析,test判断正则是否在字符串中出现过,如果出现返回true,如果没出现返回false。 let str hello world; let ret1 /e/.test(str); // true let ret2 /q/.test(str); // false 如&…...

go语言,ent库与gorm库,插入一条null值的time数据
情景介绍 使用go语言,我需要保存xxxTime的字段至数据库中,这个字段可能为空,也可能是一段时间。我采取的是统一先赋值为空,若有需要,则再进行插入(需要根据另一个字段判断是否插入) 在我的数据…...
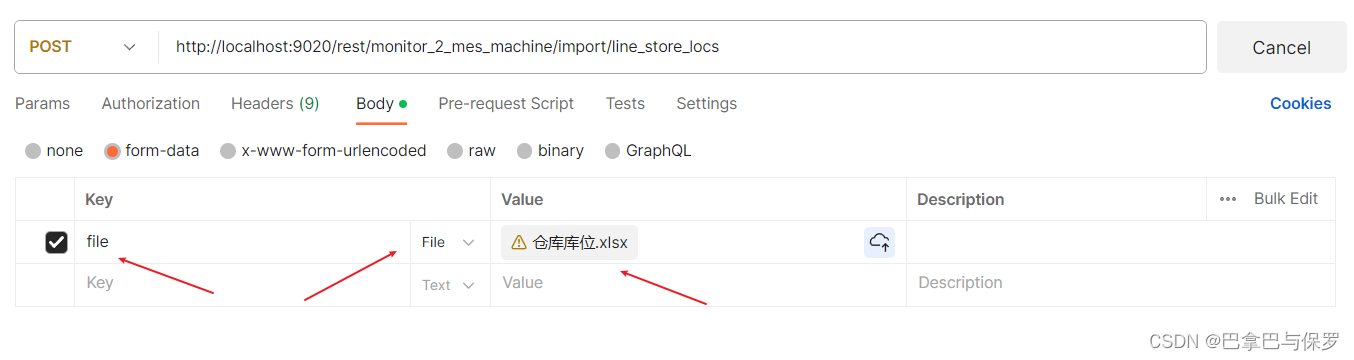
Java EasyExcel 导入代码
Java EasyExcel 导入代码 导入方法 /*** 仓库库位导入** param req* param res* param files* throws Exception*/RequestMapping(value {"/import/line_store_locs"}, method {RequestMethod.POST})ResponseBodypublic void importStoreLoc(HttpServletRequest …...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...
