图论 经典例题
1 拓扑排序
对有向图的节点排序,使得对于每一条有向边 U-->V U都出现在V之前
*有环无法拓扑排序
indegree[], nxs[];//前者表示节点 i 的入度,后者表示节点 i 指向的节点
queue = []
for i in range(n):if indege[i] == 0: queue.add(i)// 入度为0的节点加入队列
while queue:curnode = queue.popleft()for nx in nxs[curnode]:indegre[nx] -= 1;if indegre[nx] == 0:queue.add(nx);207 课程表1
#include <vector>
#include <deque>using namespace std;class Solution {
public:bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {// 邻接表vector<vector<int>> nxs(numCourses, vector<int>());// 入度数组vector<int> indegree(numCourses, 0);// 填充入度数组和邻接表for (auto pre : prerequisites) {int a = pre[0];int b = pre[1];// a 的入度增加indegree[a]++;// 将 b 加入 a 的邻接表nxs[b].push_back(a);}deque<int> q;// 1.找到入度为0的点for (int i = 0; i < numCourses; i++) {if (indegree[i] == 0) {q.push_back(i);}}// 2.迭代,更新入度while (!q.empty()) {int curr = q.front();q.pop_front();numCourses--; // 完成一个课程for (int neighbor : nxs[curr]) {if (--indegree[neighbor] == 0) {q.push_back(neighbor);}}}// 如果所有课程都完成了,则返回 truereturn numCourses == 0;}
};210 课程表II
class Solution {
public:vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {// 邻接表vector<vector<int>> nxs (numCourses, vector<int>());// 入度数组vector<int> indegree (numCourses);// 填充入度数组和邻接表for (auto pre : prerequisites) {int a = pre[0];int b = pre[1];indegree[a]++;nxs[b].push_back(a);}vector<int> res;deque<int> q;int index = 0;for (int i = 0; i < numCourses; ++i) {if (indegree[i] == 0) {q.push_back(i);}}while (!q.empty()) {int k = q.front();q.pop_front();res.push_back(k);index++;for (auto neg : nxs[k]) {if (--indegree[neg] == 0) {q.push_back(neg); }}}if (index != numCourses) {return vector<int>();}else{return res;} }
};310 最小高度树
依次删去度数为 1 的点
class Solution {
public:vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {// 找到使得树的高度最小的节点// 找到最中间的点if (n == 1) return vector<int>({0});// 储存度数,而非入度vector<int> degrees(n, 0);// 邻接表vector<vector<int>> adjacencyList(n, vector<int>());for (auto edge : edges) {int a = edge[0];int b = edge[1];degrees[a]++;degrees[b]++;adjacencyList[a].push_back(b);adjacencyList[b].push_back(a);}// 队列,储存入度为 1deque<int> q;// 找到度数为 1 的点for (int i = 0; i < n; ++i) {if (degrees[i] == 1) {q.push_back(i);}}vector<int> res;// 遍历所有边缘节点while (!q.empty()) {res.clear();// 层序更新,这一批点处理完之后,先看结果对不对int len = q.size();for (int i = 0; i < len; ++i) {int node = q.front();q.pop_front();res.push_back(node);// 更新两个矩阵for (auto nex : adjacencyList[node]) {degrees[nex]--;if (degrees[nex] == 1){q.push_back(nex);}}}}return res;}
};
802 逆向拓扑
找到不能进入环的点,跟它在不在环里面没关系
有向图找环
从出度为 0 的点出发,它们不可能在环中
class Solution {
public:vector<int> eventualSafeNodes(vector<vector<int>>& graph) {int n = graph.size();// 出度vector<int> outdegree(n);// 逆向邻接表vector<vector<int>> pre_nodes(n, vector<int>());for (int i = 0; i < n; ++i) {for (auto nx : graph[i]) {// i --> nxoutdegree[i]++;pre_nodes[nx].push_back(i);}}deque<int> q;// 找到出度为 0 的点for (int i = 0; i < n; ++i) {if (outdegree[i] == 0) {q.push_back(i);}}// 储存结果vector<int> res;while (!q.empty()) {int node = q.front();q.pop_front();res.push_back(node);for (auto nex : pre_nodes[node]) {outdegree[nex]--;if (outdegree[nex] == 0) {q.push_back(nex);}}}sort(res.begin(), res.end());return res;}
};2 并查集
查找连通块的数量
int[] fa;void init(int n) {fa = new int[n];// 初始化for (int i = 0; i < n; ++i) fa[i] = i;// 遍历,都指向自己
}// 0 和 3 是亲戚,则 0 和 3建立链接
int find(int x) {// 如果 x 是自己的 boss 则返回 x// 如果不是,则 return x == fa[x] ? x : (fa[x] = find(fa[x]));// 是否是根节点
}void union(int x, int y) {fa[find(x)] = find(y);// 连通
} vector<int> fa; // 并查集的父节点数组// 初始化并查集,设置每个节点的父节点为自己// 0 -- n-1void init(int n) {fa.resize(n);for (int i = 0; i < n; ++i) {fa[i] = i;}}// 查找节点x所在的集合的根节点,同时进行路径压缩int find(int x) {return x == fa[x] ? x : (fa[x] = find(x));}// 合并两个节点所在的集合void uni(int x, int y) {fa[find(x)] = find(y);}构建并查集的操作基本都是一样的
1.查询根节点 + 路径压缩
2.合并块
题眼一般是多个集合的合并
547 省份数量
并查集 + 求连通块的数量
class Solution {
public:vector<int> fa;// 初始化 n 个城市的父节点为它们自己void init(int n) {fa.resize(n, 0);for (int i = 0; i < n; ++i) {fa[i] = i;}}// 找 x 的夫节点int find(int x) {return x == fa[x] ? x : (fa[x] = find(fa[x]));}// 合并void uni(int x, int y) {fa[find(x)] = find(y);}// 判断多少个根节点int findCircleNum(vector<vector<int>>& isConnected) {int n = isConnected.size();// 初始化init(n);for (int i = 0; i < n; ++i){for (int j = i + 1; j < n; ++j) {if (isConnected[i][j] == 1) uni(i, j);}}// 检查最后有几个点的父节点是它自己,即根的数目int cnt = 0;for (int i = 0; i < n; ++i) {if (fa[i] == i) {cnt++;}}return cnt;}
};684 冗余连接
根据父节点的特点找冗余路径
class Solution {
public:vector<int> fa;// 节点是 1 -- nvoid init(int n) {fa.resize(n + 1, 0);for (int i = 1; i <= n; ++i) {fa[i] = i;}}int find(int x) {return fa[x] == x ? x : find(fa[x]);}void uni(int x, int y) {fa[find(x)] = find(y);}vector<int> findRedundantConnection(vector<vector<int>>& edges) {int n = edges.size();init(n);for (auto edge : edges) {int a = edge[0];int b = edge[1];// 如果父类节点都一样,那么找到了冗余路径if (find(a) == find(b)) {return edge;} else {uni(a, b);}}return vector<int>();}
};1319
先连通,看连通块的数量,连接 n 个块需要 n - 1 个边
class Solution {
public:vector<int> fa;void init(int n) {fa.resize(n);for (int i = 0; i < n; ++i) {fa[i] = i;}}int find(int x) {return fa[x] == x ? x : (fa[x] = find(fa[x]));}void uni(int x, int y) {fa[find(x)] = find(y);}int makeConnected(int n, vector<vector<int>>& connections) {// 判断端点是否连通// 如果已经连通可以拆除// 连接 n 个连通块需要 n - 1 个边init(n);int cnt = 0;for (auto con : connections) {int a = con[0];int b = con[1];if (find(a) == find(b)) {cnt++;}else{uni(a, b);}}// 判断连通块的数量int num = 0; // 初始化for (int i = 0; i < n; ++i) {if (fa[i] == i) {num++;}}// 判断边是不是够用if (cnt >= num - 1) {return num - 1;}return -1;}
};水域大小
变体,需要维护连通块的数量
class Solution {
public:// 需要维护每个连通块的数量vector<int> fa;vector<int> cnts;// 只对根节点生效void init(int n) {fa.resize(n);cnts.resize(n);for (int i = 0; i < n; ++i) {fa[i] = i;cnts[i] = 1;}}int find(int x) {return fa[x] == x ? x : (fa[x] = find(fa[x]));}void uni(int x, int y) {int xp = fa[find(x)], yp = find(y);fa[xp] = yp;cnts[yp] += cnts[xp];}int getId(int x, int y, int col) {return x * col + y;}vector<int> pondSizes(vector<vector<int>>& land) {// x * col + y// 表示八个方向的方向数组vector<vector<int>> dirs = {{0, 1}, // 向右{0, -1}, // 向左{1, 0}, // 向下{-1, 0}, // 向上{1, 1}, // 右下{1, -1}, // 右上{-1, 1}, // 左下{-1, -1} // 左上};int n = land.size();int m = land[0].size();init(n * m);for (int i = 0; i < n; ++i) {for (int j = 0; j < m; ++j) {if (land[i][j] == 0) {for (auto dir : dirs) {// 遍历八个方向int nx = i + dir[0];int ny = j + dir[1];// 如果方向不越界 且 为水域if (nx < 0 || ny < 0 || nx >= n || ny >= m || land[nx][ny] != 0) {continue;}else{int id1 = getId(i, j, m);int id2 = getId(nx, ny, m);if (find(id1) != find(id2)) {uni(id1, id2);}}}}}}vector<int> res;for (int i = 0; i < n; ++i) {for (int j = 0; j < m; ++j) {int id = getId(i, j, m);if (fa[id] == id && land[i][j] == 0) {res.push_back(cnts[id]);}}}sort(res.begin(), res.end());return res;}
};721 账户合并(字符串)
建立映射 [0, a, b] 其中 0 代表人名,a 代表邮箱地址
最后还要倒过来输出
#include <vector>
#include <string>
#include <map>
#include <algorithm>class Solution {
public:// 并查集代码vector<int> fa; // 并查集的父节点数组// 初始化并查集,设置每个节点的父节点为自己void init(int n) {fa.resize(n);for (int i = 0; i < n; ++i) {fa[i] = i;}}// 查找节点x所在的集合的根节点,同时进行路径压缩int find(int x) {return x == fa[x] ? x : find(fa[x]);}// 合并两个节点所在的集合void uni(int x, int y) {fa[find(x)] = find(y);}vector<vector<string>> accountsMerge(vector<vector<string>>& accounts) {int n = accounts.size(); // 账号的数量init(n); // 初始化并查集// 邮箱到账号ID的映射map<string, int> email_accId;// 构建并查集,合并具有相同邮箱地址的账号for (int accId = 0; accId < n; accId++) {int m = accounts[accId].size(); // 当前账号的邮箱数量for (int i = 1; i < m; ++i) {string email = accounts[accId][i]; // 获取邮箱地址// 如果邮箱地址不存在,建立映射关系// if (email_accId.find(email) == email_accId.end()) {email_accId[email] = accId; } else {// 当前id和之前id合并uni(accId, email_accId[email]); // 如果邮箱地址已存在,合并账号}}}// 账号ID到邮箱的映射map<int, vector<string>> accId_emails;// 遍历所有邮箱账号,将它们归类到相同的账号ID下for (auto& pair : email_accId) {string email = pair.first;int accId = find(pair.second); // 获取根账号IDaccId_emails[accId].push_back(email);}// 构建最终的合并后的账户列表vector<vector<string>> mergedAccounts;for (auto& pair : accId_emails) {int accId = pair.first;vector<string> emails = pair.second;// 将账号ID添加到前面vector<string> mergedAccount = {accounts[accId][0]};sort(emails.begin(), emails.end()); // 对邮箱地址排序mergedAccount.insert(mergedAccount.end(), emails.begin(), emails.end());mergedAccounts.push_back(mergedAccount);}return mergedAccounts; // 返回合并后的账户列表}
};
相关文章:

图论 经典例题
1 拓扑排序 对有向图的节点排序,使得对于每一条有向边 U-->V U都出现在V之前 *有环无法拓扑排序 indegree[], nxs[];//前者表示节点 i 的入度,后者表示节点 i 指向的节点 queue [] for i in range(n):if indege[i] 0: queue.add(i)// 入度为0的节…...
Oracle数据updater如何回滚
1.查询update语句执行的时间节点 ; select t.FIRST_LOAD_TIME, t.SQL_TEXT from v$sqlarea t where to_char(t.FIRST_LOAD_TIME) > 2023-03-19/17:00:00 order by t.FIRST_LOAD_TIME desc;开启表的行迁移 alter table test enable row movement;3.回滚表数据到…...

redis开启密码验证
开启密码验证 (1)配置文件中设置 redis.conf文件里面配置requirepass参数,redis认证密码:foobared,然后重启redis服务 ./redis-cli 127.0.0.1:6379> 127.0.0.1:6379> 127.0.0.1:6379> CONFIG SET requi…...
一种删除 KubeSphere 中一直卡在 Terminating 的 Namespace--KubeSphere Logging System的简单方法
文章目录 一、问题提出二、删除方法1,获取kubesphere-logging-syste的详细信息json文件2,编辑kubesphere-logging-system.json3,执行清理命令 三、检查结果 一、问题提出 在使用 KubeSphere 的时候发现有一个日志服务KubeSphere Logging Sys…...

Flink1.17实战教程(第七篇:Flink SQL)
系列文章目录 Flink1.17实战教程(第一篇:概念、部署、架构) Flink1.17实战教程(第二篇:DataStream API) Flink1.17实战教程(第三篇:时间和窗口) Flink1.17实战教程&…...

nest定时任务调用service报错
报错: ERROR [Scheduler] ValidationError: Using global EntityManager instance methods for context specific actions is disallowed. If you need to work with the global instances identity map, use allowGlobalContext configuration option or fork() i…...
[Angular] 笔记 11:可观察对象(Observable)
chatgpt: 在 Angular 中,Observables 是用于处理异步数据流的重要工具。它们被广泛用于处理从异步操作中获取的数据,比如通过 HTTP 请求获取数据、定时器、用户输入等。Observables 提供了一种机制来订阅这些数据流,并可以在数据到达时执行相…...
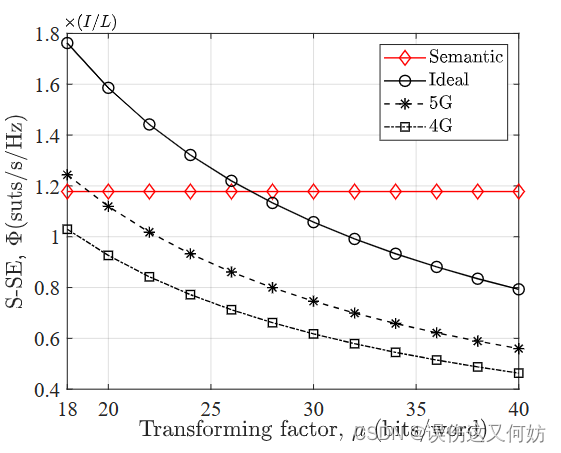
【论文阅读】Resource Allocation for Text Semantic Communications
这是一篇关于语义通信中资源分配的论文。全文共5页,篇幅较短。 目录在这里 摘要关键字引言语义通信资源分配贡献公式符号 系统模型DeepSC TransmitterTransmission ModelDeepSC Receiver 语义感知资源分配策略Semantic Spectral Efficiency (S-SE&#…...
VMware16 pro 安装openEuler-23.09-x86_64,详细操作流程+详图。
1.环境: win11, vmware16 pro, openEuler-23.09-x86_64-dvd.iso 社区版openEuler 23.09官方下载地址: openEuler下载 | 欧拉系统ISO镜像 | openEuler社区官网欧拉操作系统(openEuler, 简称“欧拉”)是面向数字基础设施的操作系统,支持服务器、云计算、…...

Mybatis 动态 SQL - script,bind,多数据库支持
script 在使用注解的映射器类中使用动态SQL时,可以使用<script>元素。例如: Update({"<script>","update Author"," <set>"," <if testusername ! null>username#{username},</if&g…...

Scikit-Learn线性回归(一)
Scikit-Learn线性回归一 1、线性回归概述1.1、回归1.2、线性1.3、线性回归1.4、线性回归的优缺点1.5、线性回归与逻辑回归2、线性回归的原理2.1、线性回归的定义与原理2.2、线性回归的损失函数3、Scikit-Learn线性回归3.1、Scikit-Learn库3.2、Scikit-Learn线性回归API3.3、Sci…...

Mybatis 动态 SQL - choose, when, otherwise
有时候我们并不希望所有的条件都生效,而是只想在多个选项中选择一个。类似于Java中的switch语句,MyBatis提供了 <choose>元素。 让我们使用上面的例子,但现在如果提供了标题,则只搜索标题;如果提供了作者&a…...
idea Spring Boot项目使用JPA创建与数据库链接
1.pom.xml文件中添加依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-jpa</artifactId></dependency><dependency><groupId>com.mysql</groupId><artifactId>…...
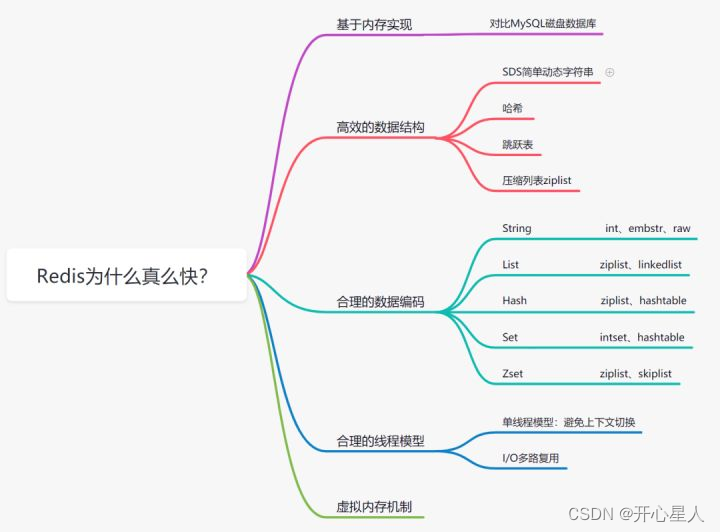
redis基础知识
学一点,整一点,基本都是综合别人的,弄成我能理解的内容 https://blog.csdn.net/liqingtx/article/details/60330555 https://blog.csdn.net/u014723137/article/details/125658176 https://redis.io/commands/ 官方命令 📌导航小助…...
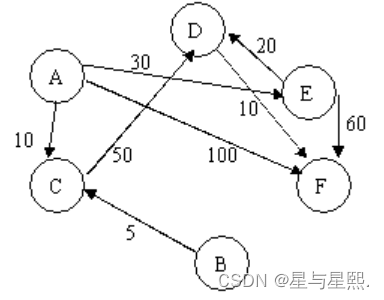
最短路径(数据结构实训)(难度系数100)
最短路径 描述: 已知一个城市的交通路线,经常要求从某一点出发到各地方的最短路径。例如有如下交通图: 则从A出发到各点的最短路径分别为: B:0 C:10 D:50 E:30 F:60 输…...
基于SSM实现的电动汽车充电网点管理系统
一、系统架构 前端:jsp | jquery | bootstrap | css 后端:spring | springmvc | jdbc 环境:jdk1.8 | mysql 二、代码及数据库 三、功能介绍 01. web端-首页 02. web端-登录 03. web端-注册 04. web端-我要充电 05. web端-个人中心-消…...
Android ImageView如何使用.svg格式图片
我们知道imageview常用的图片格式是.jpg/.png或者drawable里的部分.xml文件。但有时UI会给过来.svg格式的文件,下面讲解如何使用.svg格式图片文件 step1:AS点击File -> New -> Vector Asset step2:选中要使用的.svg文件,按需要命名和调整&#x…...

力扣热题100道-子串篇
字串 560.和为K的子数组 给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的子数组的个数 。 子数组是数组中元素的连续非空序列。 示例 1: 输入:nums [1,1,1], k 2 输出:2示例 2: 输入&a…...

day3--Shell
1.shell语法 概论 概论 shell是我们通过命令行与操作系统沟通的语言。shell脚本可以直接在命令行中执行,也可以将一套逻辑组织成一个文件,方便复用。 AC Terminal中的命令行可以看成是一个“shell脚本在逐行执行”。Linux中常见的shell脚本有很多种&…...

【数据结构】插入排序、选择排序、冒泡排序、希尔排序、堆排序
前言:生活中我们总是会碰到各种各样的排序,今天我们就对部分常用的排序进行总结和学习,今天的内容还是相对比较简单的一部分,各位一起加油哦! 💖 博主CSDN主页:卫卫卫的个人主页 💞 ὄ…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...
