2023年12月GESP Python五级编程题真题解析
【五级编程题1】
【试题名称】:小杨的幸运数
【问题描述】
小杨认为,所有大于等于a的完全平方数都是他的超级幸运数。
小杨还认为,所有超级幸运数的倍数都是他的幸运数。自然地,小杨的所有超级幸运数也都是幸运数。
对于一个非幸运数,小杨规定,可以将它一直+1,直到它变成一个幸运数。我们把这个过程叫做幸运化。例如,如果a=4,那么4是最小的幸运数,而1不是,但我们可以连续对1做3次+1操作,使其变为4,所以我们可以说,1幸运化后的结果是4。
现在,小样给出N个数,请你首先判断它们是不是幸运数;接着,对于非幸运数,请你将它们幸运化。
【输入描述】
第一行2个正整数a, N。
接下来 行,每行一个正整数 ,表示需要判断(幸运化)的数。
【输出描述】
输出N行,对于每个给定的x,如果它是幸运数,请输出“lucky”,否则请输出将其幸运化后的结果。
【数据规模】
对于30%的测试点,保证a,x≤100,N≤100。
对于60%的测试点,保证a,x≤10⁶。
对于所有测试点,保证a≤1,000,001;保证N≤2×10⁵;保证1≤x≤1,000,001。
【分析】
方法一
如x>=a,判是否是完全平方数或完全平方数的倍数,输出“lukey”。如 int(x⁰·⁵)= x⁰·⁵ 则为完全平方数,在Python中x**0.5//1比int(x**0.5)快3倍左右;x不是完全平方数,则完全平方数的倍数个数不超过x⁰·⁵,如是整数倍数,则求商是否是完全平方数?
对小于a或不是完全平方数或倍数的,则需要加1至大于等于a,直到是完全平方数或完全平方数的倍数,输出该数。
搜索2个完全平方数的次数不超过2001(2001*2001-2000*2000),找完全平方数倍数不超过x⁰·⁵
时间复杂度:O(n(x⁰·⁵+2001)),约2×10⁵×(1001+2001)≤6.1×10⁸,应该不会超时。
【完整代码】
a, n = [int(i) for i in input().split()] # 输入a和n
def p_square(n): # 判完全平方数或其倍数if n**0.5 == n**0.5//1:return Trueelse:for i in range(2,int(x**0.5)+1): # 倍数不超过int(x**0.5)if x // i == x / i and (x//i)**0.5 == (x//i)**0.5//1:return Trueelse:return False
for i in range(n): # 循环输入并处理n个数x = int(input()) # 输入xtf = Falseif x >= a:if p_square(x): # 如果是完全平方数或其倍数print('lucky') # 输出lucky tf = Trueif not tf: # 如果是则需要加1while True:x += 1if x >= a:if p_square(x): # 直到是完全平方数或其倍数print(x) # 输出该数break【运行结果】

方法二
先建完全平方数和其倍数表(简称lucky表),将可能的数值范围内的完全平方数和其倍数纳入表中,如直接从表的x位置(索引)中找到的数=x,则输出“lucky”,否则输出该数。
因为题目给出a≤1,000,001,N≤2×10⁵,x≤1,000,001,所以最大的完全平方数不超过1001*1001,故先生成1001*1001+1元素为0的列表,在1~1001的平方大于等于a的位置填上平方数(lucky数),并在其倍数位置填上相应倍数值(lucky数)。对于0值用后面与其最接近的lucky数填充。输了直接用x作为索引查询,如x作为索引的值是x,则a是lucky数,输出“lucky”,否则输出x作为索引的值。
时间复杂度:小于O(4x),主要用于建表,1001×1001+1001×2001+2×10⁵<3.3×10⁶。
【完整代码】
a, n = [int(i) for i in input().split()] # 输入a和n
max_ly = 1001 * 1001 # 最大的lucky数不超过此数,x≤1000001
nr_ly = [0 for i in range(max_ly + 1)] # 生成max_ly+1个元素为0的列表
for i in range(1, int(max_ly**0.5)+1):if i*i >= a: # 大于等于a的完全平方数元素位置填入此数nr_ly[i*i] = i*ifor j in range(i*i + i*i, max_ly, i*i): # 其倍数元素位置也填入其倍数nr_ly[j] = j
for i in range(max_ly, 0, -1): # 两个lucky数之间最近的lucky数是后面的数if not nr_ly[i]: # 如i是lucky数则有值,否则为0nr_ly[i] = nr_ly[i + 1] # 0值则填入其后面的数(最接近的lucky数)
for i in range(n): # 输入n个xx = int(input()) # 输入xif nr_ly[x] == x: # 如果x是lucky数输出“lucky”print("lucky")else:print(nr_ly[x]) # 否则输出最接近的lucky数(即x+1至lucky数)【运行结果】

【五级编程题2】
【试题名称】:烹饪问题
【问题描述】
有N种食材,编号从0至N-1,其中第i种食材的美味度为ai。
不同食材之间的组合可能产生奇妙的化学反应。具体来说,如果两种食材的美味度分别为x和y,那么它们的契合度为x and y。
其中,and运算为按位与运算,需要先将两个运算数转换为二进制,然后在高位补足 ,再逐位进行与运算。例如,12与6的二进制表示分别为1100和0110,将它们逐位进行与运算,得到0100,转换为十进制得到4,因此12 and 6 = 4。在 C++ 或 Python 中,可以直接使用 & 运算符表示与运算。
现在,请你找到契合度最高的两种食材,并输出它们的契合度。
【输入描述】
第一行一个整数N,表示食材的种数。
接下来一行N个用空格隔开的整数,依次为a0,…, aN-1,表示各种食材的美味度。
【输出描述】
输出一行一个整数,表示最高的契合度。
【数据规模】
对40%的测试点保证N≤1,000。
对所有测试点保证N≤10⁶,0≤ai≤2,147,483,647(2³¹-1)。
【分析】
方法一
由于0≤ai≤2,147,483,647,所以(ai & aj)i≠j≥0,因此结果最大值的初值可定义为0。因为ai & aj = aj & ai,先取第1个与其它N-1个数进行按位与运算,如大于结果就赋给结果(求两数按位与的最大值),再取第2个与其后N-2个数进行按位与运算,如大于结果就赋给结果(求两数按位与的最大值),以此类推,直到所有数据都计算并比较大小。此解法时间复杂度为O(N²),可以解决40%多的数据,当N≥10⁴就可能超时。
【完整代码】
n = int(input()) # 输入n
a = [int(i) for i in input().split()] # 输入n个食材的美味度
ans = 0 # 初值为0
for i in range(n-1): # 0≤i<n-1for j in range(i+1,n): # i+1≤j<nif a[i] & a[j] > ans: # a的下标为1~n-1ans = a[i] & a[j] # ans为两种食材的美味度的最大值
print(ans) # 输出结果【运行结果】

方法二
因为ai≤2,147,483,647(2³¹-1),最多31位二进制,从最高位开始枚举,时间复杂度O(31N),可以解决所有数据,不超时。
【完整代码】
n = int(input()) # 输入n
a = [int(i) for i in input().split()] # 输入n个食材的美味度
ans = 0
for i in range(30,-1,-1): # 从最高位开始枚举ans += 2**i # 加上当前二进制位为1cnt = 0 # 统计数量for j in range(n): # 遍历所有数if (ans & a[j] == ans):cnt += 1if cnt < 2: # 两个以下ans -= 2**i # 这一位为0(原加1,现减去1)
print(ans) # 输出结果【运行结果】

相关文章:

2023年12月GESP Python五级编程题真题解析
【五级编程题1】 【试题名称】:小杨的幸运数 【问题描述】 小杨认为,所有大于等于a的完全平方数都是他的超级幸运数。 小杨还认为,所有超级幸运数的倍数都是他的幸运数。自然地,小杨的所有超级幸运数也都是幸运数。 对于一个…...
探索Apache Commons Imaging处理图像
第1章:引言 大家好,我是小黑,咱们今天来聊聊图像处理。在这个数字化日益增长的时代,图像处理已经成为了一个不可或缺的技能。不论是社交媒体上的照片编辑,还是专业领域的图像分析,图像处理无处不在。而作为…...

【11】ES6:async/await
一、概念 async/await 是 ES2017(ES8)的新特性,它是一种基于 Promise 实现的异步编程方式。async/await 也是一种语法糖。 1、async/await 实现了用同步方式来写异步代码(promise是链式调用形式写异步代码) 2、asyn…...

深入理解Java集合框架
导语: Java集合框架是Java提供的一组用于管理对象的类和接口,它是Java编程中非常重要的一部分。Java集合框架通过提供诸如List、Set、Map等数据结构,为程序员提供了一种方便、高效的管理对象的方式。本文将深入理解Java集合框架,包…...

极智嘉加快出海发展步伐,可靠产品方案获客户认可
2023年,国内本土企业加快出海征程,不少企业在出海发展中表现出了优越的集团实力与创新的产品优势,有力彰显了我国先进的科技研发实力。作为全球仓储机器人引领者,极智嘉(Geek)也在不断加快出海发展步伐&…...

运动目标检测方法的概述
目录 ① 光流法 ② 帧差法 ③ 背景差分法 ④ 混合高斯模型法 ⑤ 总结 运动目标检测技术的应用十分的广泛,尤其是在智能视频监控领域。运动目标检测为后续的图像处理等操作提供了基础,在某种程度上,决定了整个系统的性能。运动目标检测&a…...

【Qt-Edit】
Qt编程指南 ■ QTextEdit■ QLineEdit■ QLineEdit 设置正则表达式■ QPlainTextEdit■ QKeySequenceEdit■ QList<QLineEdit *> edits■■■ QTextEdit /* 实例和对象,设置位置和显示大小 */ textEdit = new QTextEdit(this)...

vue data变量不能以“_”开头,否则会产生很多怪异问题
1、 比如给子组件赋值,子组件无法得到这个值(也不是一直无法得到,设置后this.$forceUpdate() 居然可以得到), 更无法watch到 <zizujian :config"_config1"> </zizujian>this._config1 { ...…...

解释RestFUL API,以及如何使用它构建web程序
RESTful API(Representational State Transfer)是一种基于网络的软件架构风格,用于构建分布式系统。它利用 HTTP 协议中的各种方法(如 GET、POST、PUT、DELETE)来对资源进行操作,使得不同应用程序能够相互通…...
文件下载输出zip文件
文件下载输出成zip文件: 1、前端整个按钮,调js方法:(参数:param,需要下载的id,用逗号拼接) var param "?dto.id";//需要自己拼接param window.location.href "<%basePat…...
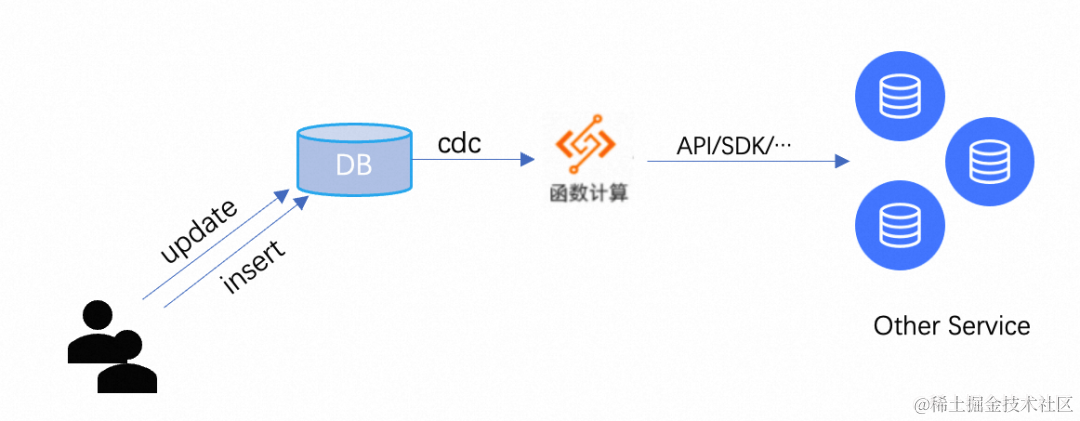
构建高效数据流转的 ETL 系统:数据库 + Serverless 函数计算的最佳实践
作者:柳下 概述 随着企业规模和数据量的增长,数据的价值越来越受到重视。数据的变化和更新变得更加频繁和复杂,因此及时捕获和处理这些变化变得至关重要。为了满足这一需求,数据库 CDC(Change Data Captureÿ…...
鸿蒙开发(二)- 鸿蒙DevEco3.X开发环境搭建
上篇说到,鸿蒙开发目前势头旺盛,头部大厂正在如火如荼地进行着,华为也对外宣称已经跟多个厂商达成合作。目前看来,对于前端或客户端开发人员来说,掌握下鸿蒙开发还是有些必要性的。如果你之前是从事Android开发的&…...

Openslide安装
文章目录 安装open-slide python下载openslide二进制文件解压到Anaconda的library目录下配置环境变量在py文件中添加以下语句即可 官网链接 安装open-slide python 表面上这样就可以导入了但事实上会遇到 Couldn’t locate OpendSlide DLL的问题,openslide必须独立安…...

【ES】Elasticsearch常见问题与解决(持续更新)
目录 Elasticsearch常见问题 1. 集群健康问题 2. 性能问题 3. 映射问题 4. 分片问题 5. 内存问题 6. 硬件问题 7. 配置问题 8. 安全问题 9. 网络问题 10. 版本不兼容 Elasticsearch日常使用小结 【Q】离线告警,有IP已离线 【Q】统计某个应用的某个索引…...

2023.12.29 Python面向对象 封装_继承_多台
目录 1.封装-私有与公开权限 2.继承 2.1多继承 2.2继承多层传递 2.3重写父类方法 2.4继承链 2.5禁止私有继承 3.多态 4.总结 1.封装-私有与公开权限 公开属性、公开方法:随便调用 私有属性、私有方法: 只能在类定义的内部调用 以两个下划线开头__的…...
通过自然语言处理增强推荐系统:协同方法
一、介绍 自然语言处理 (NLP) 是人工智能的一个分支,专注于使机器能够以有意义且有用的方式理解、解释和响应人类语言。它包含一系列技术,包括情感分析、语言翻译和聊天机器人。 另一方面,推荐系统(RecSys)是旨在向用户…...

大创项目推荐 深度学习OCR中文识别 - opencv python
文章目录 0 前言1 课题背景2 实现效果3 文本区域检测网络-CTPN4 文本识别网络-CRNN5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 **基于深度学习OCR中文识别系统 ** 该项目较为新颖,适合作为竞赛课题方向,…...
Python经典游戏 唤醒你童年记忆
这些游戏你玩过几个? 1.贪吃蛇2.吃豆人3.加农炮4.四子棋5. Fly Bird<font color #f3704ab>6.记忆:数字对拼图游戏(欢迎挑战!用时:2min)7.乒乓球8.上课划水必备-井字游戏(我敢说100%的人都…...

什么是骨传导耳机?骨传导能保护听力吗?
骨传导耳机是一种非常特殊的蓝牙耳机,它通过骨传导技术将声音直接传送到内耳。这种技术不同于传统耳机,它不通过空气传送声音,而是通过头骨的振动来传送声音。 并且骨传导耳机能够在一定程度上起到保护听力的作用,主要是因为它们不…...
使用electron属性实现保存图片并获取图片的磁盘路径
在普通的网页开发中,JavaScript由于安全性的考虑,通常是无法直接获取到客户端的磁盘路径的。浏览器出于隐私和安全原因对此类信息进行了限制。 在浏览器环境下,JavaScript主要通过Web APIs来与浏览器进行交互,而这些API通常受到浏…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
