2014,TEVC,A competitive swarm optimizer for large scale optimization(CSO)
PSO 分析(从而引入 CSO)
CSO (competitive swarm optimizer) 算法是在PSO (particle swarm optimization) 算法的基础上改进而来的。PSO算法是一种功能强大、应用广泛的群体智能算法,主要用来解决优化问题。PSO算法包含一个粒子群,粒子群里面的每个粒子均有1个 n n n维位置变量和1个 n n n维速度变量。在算法的每次迭代过程中,每个粒子的位置变量 X i X_i Xi 和速度变量 V i V_i Vi通过以下公式进行更新:
V i ( t + 1 ) = ω V i ( t ) + c 1 R 1 ( t ) ( p b e s t i ( t ) − X i ( t ) ) + c 2 R 2 ( t ) ( g b e s t ( t ) − X i ( t ) ) X i ( t + 1 ) = X i ( t ) + V i ( t + 1 ) \begin{gathered}V_i\left(t+1\right)=\omega V_i\left(t\right)+c_1R_1\left(t\right)(pbest_i\left(t\right)-X_i\left(t\right))+c_2R_2\left(t\right)(gbest(t)-X_i\left(t\right))\\\\\\X_i\left(t+1\right)=X_i\left(t\right)+V_i\left(t+1\right)\end{gathered} Vi(t+1)=ωVi(t)+c1R1(t)(pbesti(t)−Xi(t))+c2R2(t)(gbest(t)−Xi(t))Xi(t+1)=Xi(t)+Vi(t+1)
其中 t t t是当前迭代数, ω \omega ω是惯性权重, c 1 c_1 c1和 c 2 c_2 c2是加速度系数, R 1 ( t ) R_1(t) R1(t)和 R 2 ( t ) R_2\left(t\right) R2(t)是两个向量,向量中每个元索取值范围为 [ 0 , 1 ] n [0,1]^n [0,1]n, p b e s t i ( t ) pbest_i(t) pbesti(t) 是第 i i i个粒子的历史最优解, g b e s t ( t ) gbest(t) gbest(t)是所有粒子的历史最优解。 c 1 R 1 ( t ) ( p b e s t i ( t ) − X i ( t ) ) c_1R_1(t)(pbest_i(t)-X_i(t)) c1R1(t)(pbesti(t)−Xi(t))为认知部分, c 2 R 2 ( t ) ( g b e s t ( t ) − X i ( t ) ) c_2R_2(t)(gbest(t)-X_i(t)) c2R2(t)(gbest(t)−Xi(t))为社会部分。
当优化问题存在大量局部最优值和具有高维特点时,传统PSO算法在处理此类问题时会过早收敛,从而导致其优化效果不佳。首先来看 g b e s t gbest gbest 对算法收敛过程的影响,将上述公式进行变换,可得:
V i ( t + 1 ) = ω V i ( t ) + θ 1 ( p 1 − X i ( t ) ) \left.V_i\left(t+1\right)=\omega V_i\left(t\right)+\theta_1\left(p_1\right.-X_i\left(t\right)\right) Vi(t+1)=ωVi(t)+θ1(p1−Xi(t))
其中,
θ 1 = c 1 R 1 ( t ) + c 2 R 2 ( t ) \theta_1\:=c_1\:R_1\left(t\right)+c_2\:R_2\left(t\right) θ1=c1R1(t)+c2R2(t)
p 1 = c 1 R 1 ( t ) c 1 R 1 ( t ) + c 2 R 2 ( t ) p b e s t i ( t ) + c 2 R 2 ( t ) c 1 R 1 ( t ) + c 2 R 2 ( t ) g b e s t ( t ) p_{1}\:=\:\frac{c_{1}R_{1}\left(t\right)}{c_{1}R_{1}\left(t\right)+c_{2}R_{2}\left(t\right)}pbest_{i}\left(t\right)+\frac{c_{2}R_{2}\left(t\right)}{c_{1}R_{1}\left(t\right)+c_{2}R_{2}\left(t\right)}gbest(t) p1=c1R1(t)+c2R2(t)c1R1(t)pbesti(t)+c1R1(t)+c2R2(t)c2R2(t)gbest(t)
p 1 p_1 p1和 X i X_i Xi的差决定了粒子群的种群多样性,而 p b e s t i pbest_i pbesti 和 g b e s t gbest gbest的取值多样性决定了 p 1 p_1 p1取值的多样性。由于 g b e s t gbest gbest的影响,随着送代过程的继续,粒子逐渐向 g b e s t gbest gbest靠拢,这导致 p b e s t i pbest_i pbesti逐渐接近 g b e s t gbest gbest,进而导致粒子群的种群多样性大幅降低。 p 1 p_1 p1在很大程度上决定着传统PSO 算法在搜索过程中的勘探能力和开采能力。
为了解决传统PSO算法的过早收敛问题,本文提出了CSO算法。该算法去掉了 p b e s t i pbest_i pbesti和 g b e s t gbest gbest两个变量,引入了粒子间的成对竞争机 制。在该机制中,竞争失败的粒子将向竞争胜利的粒子学习,而不是向 p b e s t i pbest_i pbesti和 g b e s t gbest gbest学习,这将较好地解决传统PSO算法的过早收敛问
题。
基本理论
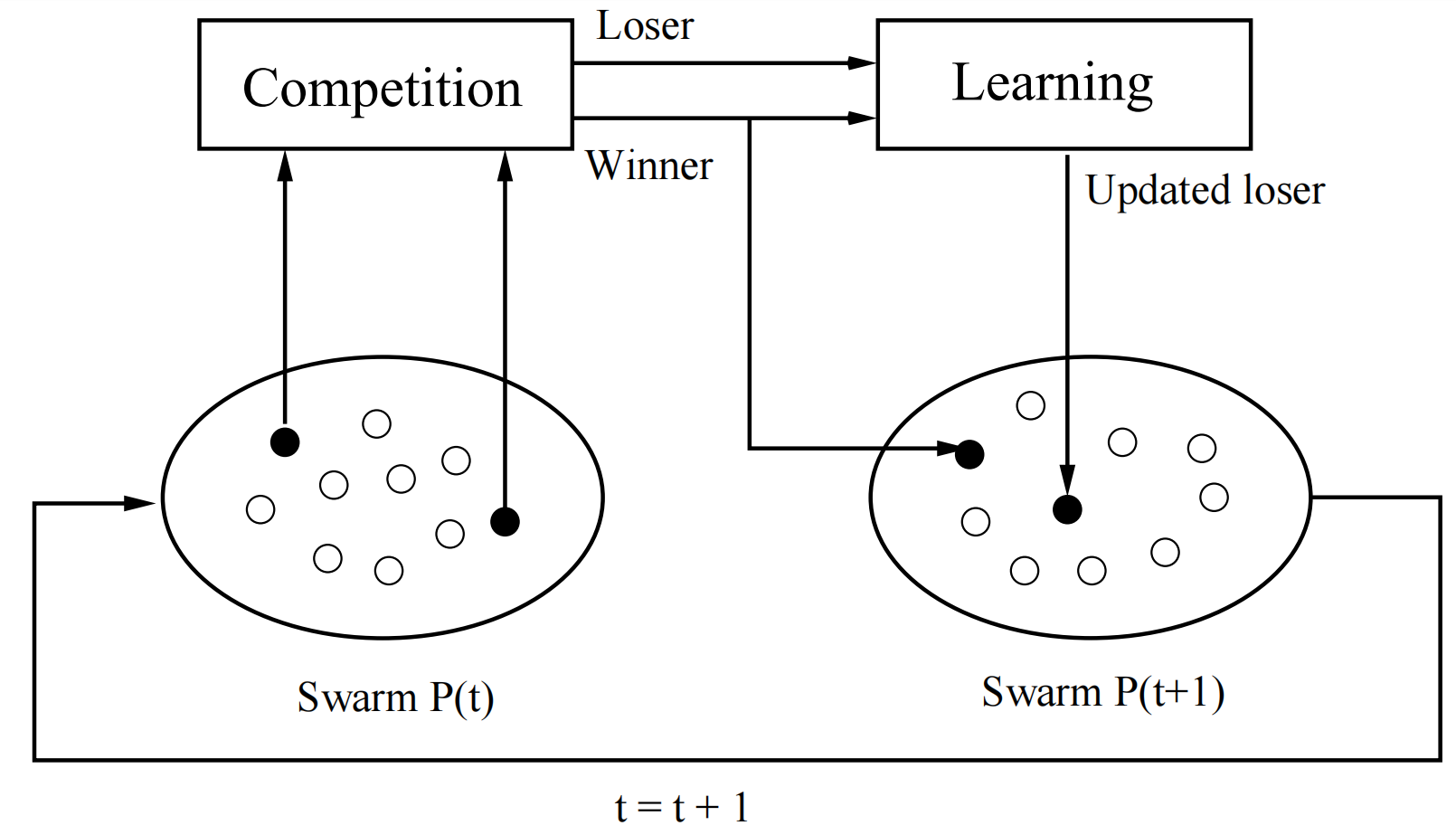
CSO 算法的总体思想如图所示。在每一次迭代过程中,随机从粒子群 P ( t ) P(t) P(t)中选择一对粒子进行竞争。竞争成功的粒子直接进入下一次迭代,竞争失败的粒子将向竞争成功的粒子学习并更新自己的位置变量和速度变量。该操作完成后,将这一对粒子从粒子群 P ( t ) P(t) P(t)中剔除, 将竞争成功的粒子和更新后的失败粒子加入到粒子群 P ( t + 1 ) P(t+1) P(t+1)中。当所有粒子从粒子群 P ( t ) P(t) P(t)中移到粒子群 P ( t + 1 ) P(t+1) P(t+1)中后,算法进入下一次迭代。根据上图可知,每一次迭代将会使粒子群 P P P中一半的粒子得到更新。
竞争失败的粒子的速度变量和位置变量更新如以下公式所示:
V l , k ( t + 1 ) = R 1 ( k , t ) V l , k ( t ) + R 2 ( k , t ) ( X w , k ( t ) − X l , k ( t ) ) + φ R 3 ( k , t ) ( X ˉ k ( t ) − X l , k ( t ) ) \begin{aligned}V_{l,k}\left(t+1\right)&=R_1\left(k,t\right)V_{l,k}\left(t\right)+R_2\left(k,t\right)(X_{w,k}\left(t\right)-X_{l,k}\left(t\right))+\varphi R_3\left(k,t\right)(\bar{X}_k\left(t\right)-X_{l,k}\left(t\right))\end{aligned} Vl,k(t+1)=R1(k,t)Vl,k(t)+R2(k,t)(Xw,k(t)−Xl,k(t))+φR3(k,t)(Xˉk(t)−Xl,k(t))
X l , k ( t + 1 ) = X l , k ( t ) + V l , k ( t + 1 ) \begin{aligned}X_{l,k}\left(t+1\right)&=X_{l,k}\left(t\right)+V_{l,k}\left(t+1\right)\end{aligned} Xl,k(t+1)=Xl,k(t)+Vl,k(t+1)
其中, X w , k ( t ) X_{w,k}(t) Xw,k(t)表示第 t t t代的第 k k k轮竞争中竞争成功粒子的位置, X l , k ( t ) X_{l,k}(t) Xl,k(t)表示第 t t t代的第 k k k轮竞争中竞争失败粒子的位置, V l , k ( t ) V_{l,k}(t) Vl,k(t)表示第 t t t 代的第 k k k轮竞争中竞争失败粒子的速度, R 1 ( k , t ) R_1(k,t) R1(k,t)、 R 2 ( k , t ) R_2(k,t) R2(k,t)、 R 3 ( k , t ) ∈ [ 0 , 1 ] R_3(k,t)\in[0,1] R3(k,t)∈[0,1]分别表示算法第 t t t次迭代的第 k k k轮竞争中随机生成的向量。
X ˉ k ( t ) \bar{X}_k\left(t\right) Xˉk(t)表示第 t t t代的第 k k k轮竞争中相关粒子的位置平均值,它分为全局版本和局部版本。
- X ˉ k g ( t ) \bar{X}_k^g(t) Xˉkg(t)表示 P ( t ) P(t) P(t)中所有粒子的位置平均值,是全局版本。
- X ˉ l , k l ( t ) \bar{X}_{l,k}^l(t) Xˉl,kl(t)表示在竞争失败粒子的预定义邻域内所有粒子的位置平均值,是局部版本。领域控制可以增加粒子群的种群多样性,这可能会提高CSO算法的搜索能力。
算法流程

1.3 勘探能力与开采能力分析
粒子群优化算法 PSO 是一种模拟自然界生物群体行为的随机搜索算法,它通过调整粒子的速度和位置来寻找最优解。在这个过程中,粒子需要平衡两种能力:
- 勘探能力(Exploration Ability):指粒子在搜索空间中探索新区域的能力,也就是全局寻优能力。勘探能力越强,粒子越容易跳出局部最优解,找到更好的解。
- 开采能力(Exploitation Ability):指粒子在搜索空间中开发已知区域的能力,也就是局部寻优能力。开采能力越强,粒子越容易收敛到最优解,提高搜索精度。
粒子群优化算法 PSO 的参数设置和拓扑结构都会影响粒子的勘探能力和开采能力,因此需要根据不同的优化问题进行合理的调整。一般来说,算法在前期需要较强的勘探能力,而在后期需要较强的开采能力,以达到最佳的性能。

首先分析一下CSO算法的勘探能力,将上述公式转换:
V i ( t + 1 ) = R 1 ( k , t ) V i ( t ) + θ 2 ( p 2 − X i ( t ) ) \begin{aligned} &\left.V_i\left(t+1\right)=R_1\left(k,t\right)V_i\left(t\right)+\theta_2\left(p_2\right.-X_i\left(t\right)\right) \\ \end{aligned} Vi(t+1)=R1(k,t)Vi(t)+θ2(p2−Xi(t))
θ 2 = R 2 ( k , t ) + φ R 3 ( k , t ) \theta_{2} =R_2\left(k,t\right)+\varphi R_3\left(k,t\right) θ2=R2(k,t)+φR3(k,t)
p 2 = R 2 ( k , t ) R 2 ( k , t ) + φ R 3 ( k , t ) X w ( t ) + φ R 3 ( k , t ) R 2 ( t ) + φ R 3 ( k , t ) X ˉ ( t ) p_{2} =\frac{R_2\left(k,t\right)}{R_2\left(k,t\right)+\varphi R_3\left(k,t\right)}X_w\left(t\right)+\frac{\varphi R_3\left(k,t\right)}{R_2\left(t\right)+\varphi R_3\left(k,t\right)}\bar{X}\left(t\right) p2=R2(k,t)+φR3(k,t)R2(k,t)Xw(t)+R2(t)+φR3(k,t)φR3(k,t)Xˉ(t)
CSO算法的种群多样性是高于传统PSO算法的,因为 X w ( t ) X_w(t) Xw(t)和 X ˉ ( t ) \bar{X}(t) Xˉ(t)的取值更加地多样。下面展示CSO算法的勘探能力是如何高于传统PSO算法的。
首先看图 2, g b e s t ( t ) gbest(t) gbest(t)陷入了局部最优,在传统PSO算法中,两个被选择的粒子均会向 g b e s t ( t ) gbest(t) gbest(t)靠近,这最终使得算法陷入局部最优的陷阱,导致算法优化结果的不佳。现在去掉向 g b e s t ( t ) gbest(t) gbest(t)更新的方式,所有粒子均只向各自的 p b e s t ( t ) pbest(t) pbest(t)更新,如图 3。从图可以看出,被选择的粒子会跳出局部最优的陷阱,使得算法的勘探能力得到了提升。但是如果 p b e s t ( t ) pbest(t) pbest(t)也陷入了局部最优,如图 4,算法也会陷入局部最优的陷阱,导致算法的勘探能力下降。因此,去掉向 g b e s t ( t ) gbest(t) gbest(t) 与 p b e s t ( t ) pbest(t) pbest(t) 更新的方式,粒子的更新采用成对粒子竞争更新机制,传统PSO算法也就演变为CSO算法。如图 4,由于所有粒子分布在样本空间的不同位置,粒子的更新就变得更加多样化,非常有助于算法脱离局部最优的陷阱,从而使得算法的勘探能力大幅提升。
然后分析一下CSO算法的开采能力。CSO算法的开采阶段是在勘探阶段之后,是在勘探阶段基础上继续小规模地提高算法的优化结果。在传统的PSO算法中,有以下关系:
{ f ( g b e s t ( t ) ) ≤ f ( p b e s t w ( t ) ) ≤ f ( X w ( t ) ) f ( g b e s t ( t ) ) ≤ f ( b e s t l ( t ) ) ≤ f ( X l ( t ) ) \left.\left\{\begin{array}{c}f(gbest(t))\leq f\left(pbest_w\left(t\right)\right)\leq f\left(X_w\left(t\right)\right)\\f(gbest(t))\leq f\left(best_l\left(t\right)\right)\leq f\left(X_l\left(t\right)\right)\end{array}\right.\right. {f(gbest(t))≤f(pbestw(t))≤f(Xw(t))f(gbest(t))≤f(bestl(t))≤f(Xl(t))
随着迭代过程的继续,t 越来越大,有:
{ p b e s t w ( t ) ≈ g b e s t ( t ) p b e s t l ( t ) ≈ g b e s t ( t ) \left.\left\{\begin{array}{l}pbest_w\left(t\right)\approx gbest(t)\\pbest_l\left(t\right)\approx gbest(t)\end{array}\right.\right. {pbestw(t)≈gbest(t)pbestl(t)≈gbest(t)
然后令:

其中 p 1 ′ p_1^{\prime} p1′是 p 1 p_1 p1的数学期望, p 2 ′ p_2^{\prime} p2′是 p 2 p_2 p2在 φ = 0 \varphi=0 φ=0的数学期望。可以得到:
Δ F 2 ( t ) ≤ Δ F 1 ( t ) \Delta F_2\left(t\right)\leq\Delta F_1\left(t\right) ΔF2(t)≤ΔF1(t)
与传统PSO算法相比,CSO算法有更好的能力开发与最优粒子相接近的粒子,也就是其开发能力更好,即局部搜索能力更强。此证明过程主要与其勘探过程结合来看。
References
Cheng R, Jin Y. A competitive swarm optimizer for large scale optimization[J]. IEEE transactions on cybernetics, 2014, 45(2): 191-204.
标准 CSO
竞争粒子群(CSO)算法
相关文章:

2014,TEVC,A competitive swarm optimizer for large scale optimization(CSO)
PSO 分析(从而引入 CSO) CSO (competitive swarm optimizer) 算法是在PSO (particle swarm optimization) 算法的基础上改进而来的。PSO算法是一种功能强大、应用广泛的群体智能算法,主要用来解决优化问题。PSO算法包含一个粒子群࿰…...

【机器学习】【线性回归】梯度下降
文章目录 [toc]数据集实际值估计值估计误差代价函数学习率参数更新Python实现导包数据预处理迭代过程数据可视化完整代码 线性拟合结果代价结果 个人主页:丷从心 系列专栏:机器学习 数据集 ( x ( i ) , y ( i ) ) , i 1 , 2 , ⋯ , m \left(x^{(i)} , …...
JMeter逻辑控制器之While控制器
JMeter逻辑控制器之While控制器 1. 背景2.目的3. 介绍4.While示例4.1 添加While控制器4.2 While控制器面板4.3 While控制器添加请求4.3 While控制器应用场景 1. 背景 存在一些使用场景,比如:某个请求必须等待上一个请求正确响应后才能开始执行。或者&…...

记录 Docker 外部访问的基本操作
目录 1. 启动 docker 时挂载本地目录2. 外部访问 docker 容器 (-p/-P)3. 无法连接 docker 内 SSH 解决方案 1. 启动 docker 时挂载本地目录 # 将本地 D:/SDK 目录 挂载到 容器里的 /mnt/host 目录中 # 注意:-v /d/SDK:/mnt/host/ 必须放到 IMAGE_ID 前面才行 # …...
:BannerMessagePreference)
【Android 13】使用Android Studio调试系统应用之Settings移植(六):BannerMessagePreference
文章目录 一、篇头二、系列文章2.1 Android 13 系列文章2.2 Android 9 系列文章2.3 Android 11 系列文章三、BannerMessagePreference的移植3.1 新的问题:找不到 R.dimen.settingslib_preferred_minimum_touch_target3.2 问题分析(一)3.2.1 资源定义的位置3.2.2 检查依赖3.2…...

Python 变量
打印输出内容 print(‘rumenle’) print(‘haode’) 缩进需要tab 注释将需要注释的部分开头用# 多行注释 1、用你也可以左键选中我们需要注释的代码,松开,按:Ctrl/,就完成相同效果注释 2、把要注释的内容放到三个引号对里面 …...

ComfyUI如何中文汉化
comfyui中文地址如下: https://github.com/AIGODLIKE/AIGODLIKE-ComfyUI-Translationhttps://github.com/AIGODLIKE/AIGODLIKE-ComfyUI-Translation如何安装? 1. git安装 进入项目目录下的custom_nodes目录下,然后进入控制台,运…...
Glary Utilities Pro - 电脑系统优化全面指南:详尽使用教程
软件简介: Glary Utilities Pro 是一款全面的电脑优化工具,它旨在帮助用户提升计算机的性能和稳定性。这款软件提供了多种功能,包括系统清理、优化、修复以及保护。通过一键扫描,它可以识别并清除无用文件、临时数据、注册表错误等…...

1.4分页和排序
排序: -- 分页(limit)和排序(order by) -- 排序:升序ASC,降序DESC -- ORDER BY 通过字段排序,怎么排 -- 查询的结果根据成绩降序,升序 SELECT s.studentno,studentname,sub.subjectname,studentresult FROM student s RIGHT JO…...

Modbus转Profinet,不会编程也能用!轻松快上手!
Modbus转Profinet是一种用于工业自动化领域的通信协议转换器,可以将Modbus协议转换为Profinet协议,实现设备之间的数据交换与通信。这个工具的使用非常简单,即使没有编程经验的人也可以轻松上手。即使不会编程的人也可以轻松快速上手使用Modb…...
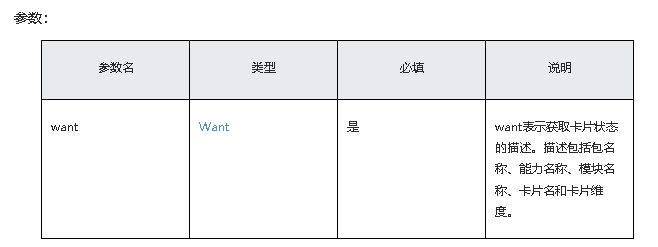
鸿蒙原生应用/元服务开发-Stage模型能力接口(十)下
ohos.app.form.FormExtensionAbility (FormExtensionAbility) 系统能力:SystemCapability.Ability.Form 示例 import FormExtensionAbility from ohos.app.form.FormExtensionAbility; import formBindingData from ohos.app.form.formBindingData; import formP…...

QT QPluginloader 加载失败,出现Unknown error 0x000000c1的问题
最近在学习Qt的插件开发,在加载插件时,一直失败,用如下代码加载并打印错误信息。 QDir dir("./testplugin.dll"); QPluginLoader pluginLoader(dir.absolutePath());//需要绝对路径 pluginLoader.load(); qDebug()<< "…...

众和策略:今年首次!A股罕见一幕
岁末,A股走出了不常见的行情。 这儿指的不单单是指数上涨。今天上午,A股逾3900只个股上涨,昨日逾4400只个股上涨,前天逾3700只个股上涨。据通达信数据显现,这种连续的普涨行情在本年还是头一次。 本年10月底…...
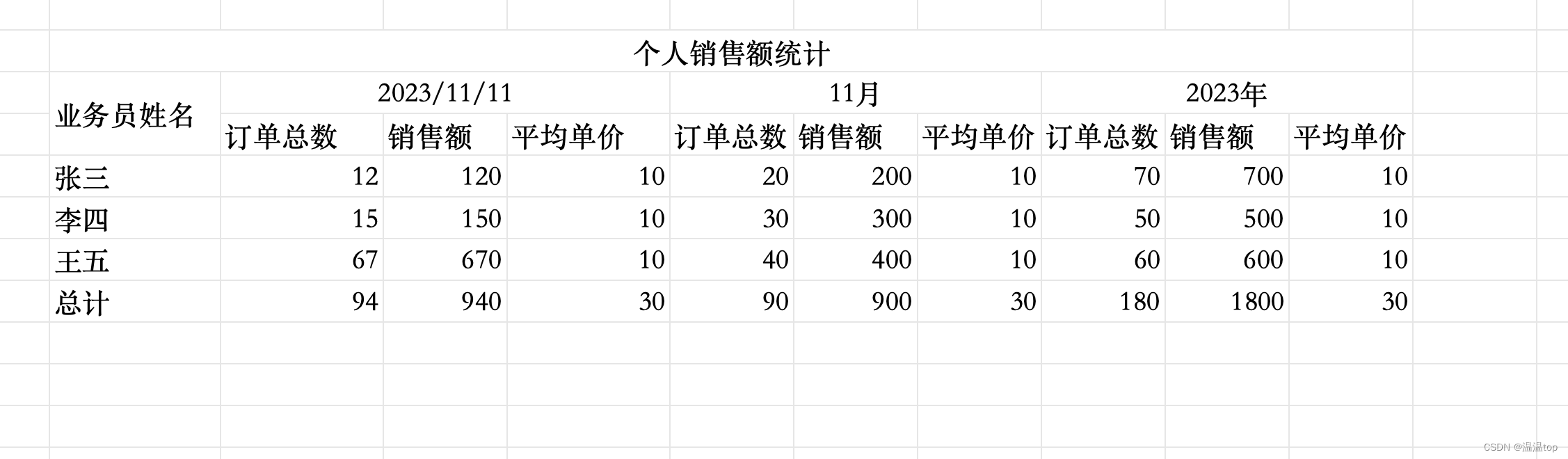
EasyExcel实现动态表头(注解实现)
要实现上述动态头,按每日统计,每月统计,每年统计。而时间是一直变化,所以我们需要表头也一直动态生成。 首先,我们需要定义所需要实体类 public class CountDayData {ExcelProperty(value "业务员姓名")p…...

什么是工厂方法模式,工厂方法模式解决了什么问题?
工厂方法模式是一种创建型设计模式,它定义了一个用于创建对象的接口,但将实际的实例化过程延迟到子类中。这样,客户端代码在不同的子类中实例化具体对象,而不是直接实例化具体类。工厂方法模式允许一个类的实例化延迟到其子类&…...
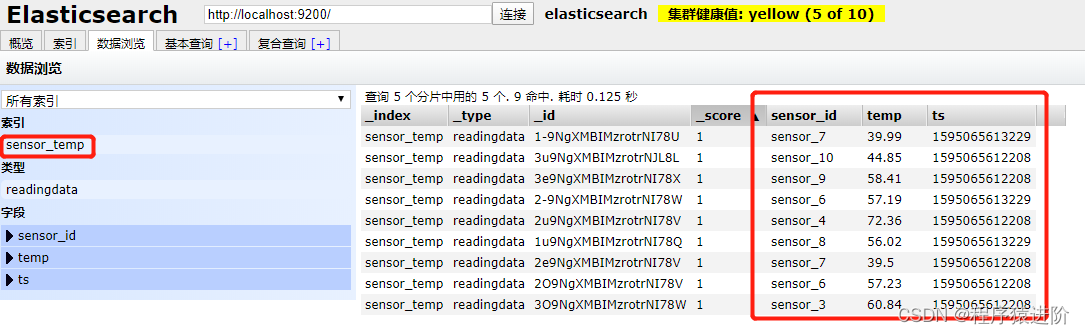
Flink 输出至 Elasticsearch
【1】引入pom.xml依赖 <dependency><groupId>org.apache.flink</groupId><artifactId>flink-connector-elasticsearch6_2.12</artifactId><version>1.10.0</version> </dependency>【2】ES6 Scala代码,自动导入的…...
web三层架构
目录 1.什么是三层架构 2.运用三层架构的目的 2.1规范代码 2.2解耦 2.3代码的复用和劳动成本的减少 3.各个层次的任务 3.1web层(表现层) 3.2service 层(业务逻辑层) 3.3dao 持久层(数据访问层) 4.结合mybatis简单实例演示 1.什么是三层架构 三层架构就是把…...

智能优化算法应用:基于厨师算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于厨师算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于厨师算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.厨师算法4.实验参数设定5.算法结果6.参考文献7.MA…...
写在2023年末,软件测试面试题总结
大家好,最近有不少小伙伴在后台留言,得准备年后面试了,又不知道从何下手!为了帮大家节约时间,特意准备了一份面试相关的资料,内容非常的全面,真的可以好好补一补,希望大家在都能拿到…...
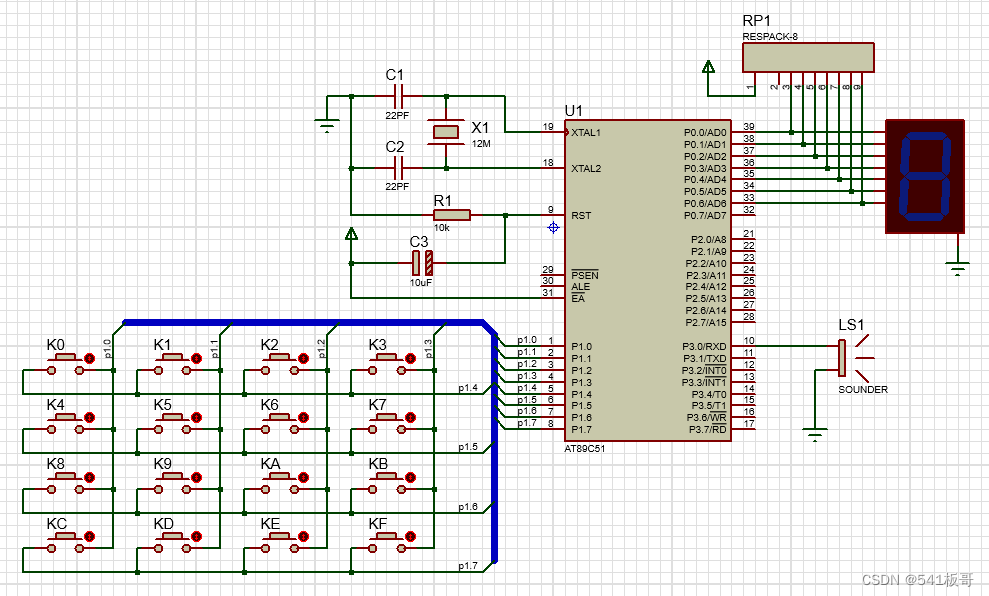
51系列--数码管显示的4X4矩阵键盘设计
本文介绍基于51单片机的4X4矩阵键盘数码管显示设计(完整Proteus仿真源文件及C代码见文末链接) 一、系统及功能介绍 本设计主控芯片选用51单片机,主要实现矩阵键盘对应按键键值在数码管上显示出来,矩阵键盘是4X4共计16位按键&…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...
