循环冗余效验码的计算方法

循环冗余效验码的计算方法
G(x):
在了解计算方法之前我们首先要明白G(x)表明的意思,这一步非常重要!
例如,G(x) = x^3 + x^2 + 1 ,该式子表明的编码是 1101 ,其中 1 可以转化为 x^0 ,随后从0开始,这一段编码的个数是 0~3 总共 4 个数字,这些数字只能用0和1表示。
而在 序号是3、2、0的位置上,它们用数字1表示,而其他的则是数字0表示。
T(x):
T(x) = M(x) + M(x)/ G(x)
具体步骤如下:

注意事项:
- 在得到信息码M(x)后,与G(x)进行的并不是除法运算,而是进行二进制的异或运算
- 其次,在进行异或运算的过程中,每次运算的开头必须是1开头,且要凑满G(x)的数字个数进行运算
- 第三,在运算完以此异或运算后,开启下一次运算前需要将M(x)未进行运算的数字往下拉,且根据第二条注意事项,遵循拉满写1,未拉满写0,这些都是写在商的位置上的。
- 第四,也是在进行运算的第一步!补0!根据G(x)的项中,最高的次幂数字进行补0,如上图G(x)的最高次幂数字是3,所以需要在M(x)的后面进行补三个0才开始运算。
- 最后,当不能再进行运算后,得出的最后的‘余数’就是需要添加到M(x)末尾使得M(x)变成T(x)的编码,当然这些编码可能会很长,所以我们要选取这段编码,而选取编码的数字个数是从右往左,且编码的个数和补了多少个0有关,例如上图,最后的编码选取了三位,因为补了三个0

相关文章:

循环冗余效验码的计算方法
循环冗余效验码的计算方法 G(x): 在了解计算方法之前我们首先要明白G(x)表明的意思,这一步非常重要! 例如,G(x) x^3 x^2 1 ,该式子表明的编…...
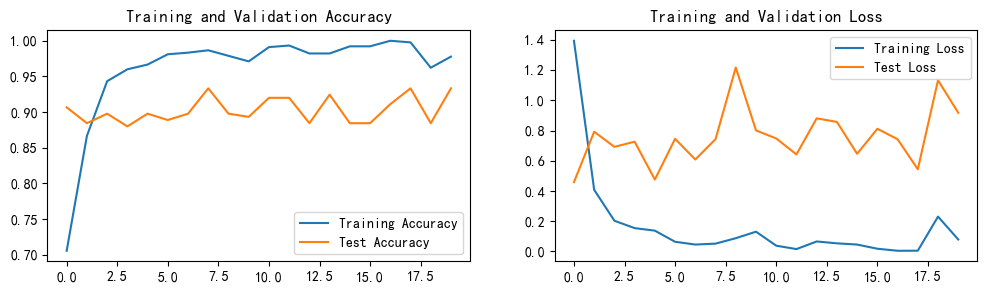
第P8周:YOLOv5-C3模块实现
>- **🍨 本文为[🔗365天深度学习训练营](https://mp.weixin.qq.com/s/rbOOmire8OocQ90QM78DRA) 中的学习记录博客** >- **🍖 原作者:[K同学啊 | 接辅导、项目定制](https://mtyjkh.blog.csdn.net/)** 一、 前期准备 1. 设…...
)
Java中常见的日志包分析(Log4j、Logback、SLF4J等)
Java中常见的日志jar包包括Log4j、Logback、SLF4J、java.util.logging等。它们各自的作用和应用场景如下: 1. Log4j 作用:Log4j是Apache的一个开源项目,提供日志记录的功能,支持多种输出目的地,如控制台、文件、GUI组…...

C++系列-第1章顺序结构-3-输出类cout
C系列-第1章顺序结构-3-输出类cout 在线练习: http://noi.openjudge.cn/ https://www.luogu.com.cn/ 总结 本文是C系列博客,主要讲述输出类cout的用法 cout介绍与基本用法 在C中,cout 是用于输出(打印)数据的工具&…...

对于智能设备的一些设想1
最近发现脑子里经常会出现一些能够偷懒的想法,希望这些点子能一点点保存下来,希望有需要的人拿走点子,不用谢 1.泡脚桶 2023年12月28日 近两年泡脚桶的风着实很大,我差点也就入坑了,于是有了一种设想,为什么…...

Large-Precision Sign using PBS
参考文献: [CLOT21] Chillotti I, Ligier D, Orfila J B, et al. Improved programmable bootstrapping with larger precision and efficient arithmetic circuits for TFHE[C]//Advances in Cryptology–ASIACRYPT 2021: 27th International Conference on the T…...

【电商项目实战】MD5登录加密及JSR303自定义注解
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是Java方文山,一个在CSDN分享笔记的博主。📚📚 🌟推荐给大家我的专栏《电商项目实战》。🎯🎯 &am…...

2014,TEVC,A competitive swarm optimizer for large scale optimization(CSO)
PSO 分析(从而引入 CSO) CSO (competitive swarm optimizer) 算法是在PSO (particle swarm optimization) 算法的基础上改进而来的。PSO算法是一种功能强大、应用广泛的群体智能算法,主要用来解决优化问题。PSO算法包含一个粒子群࿰…...

【机器学习】【线性回归】梯度下降
文章目录 [toc]数据集实际值估计值估计误差代价函数学习率参数更新Python实现导包数据预处理迭代过程数据可视化完整代码 线性拟合结果代价结果 个人主页:丷从心 系列专栏:机器学习 数据集 ( x ( i ) , y ( i ) ) , i 1 , 2 , ⋯ , m \left(x^{(i)} , …...
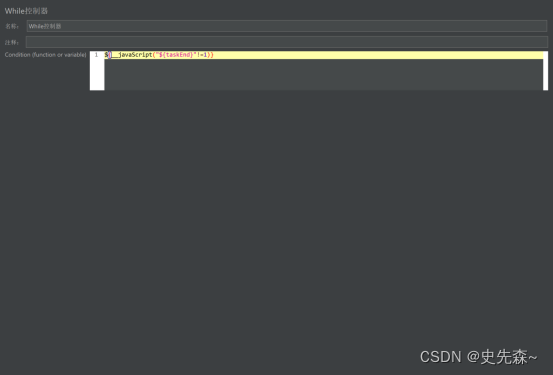
JMeter逻辑控制器之While控制器
JMeter逻辑控制器之While控制器 1. 背景2.目的3. 介绍4.While示例4.1 添加While控制器4.2 While控制器面板4.3 While控制器添加请求4.3 While控制器应用场景 1. 背景 存在一些使用场景,比如:某个请求必须等待上一个请求正确响应后才能开始执行。或者&…...

记录 Docker 外部访问的基本操作
目录 1. 启动 docker 时挂载本地目录2. 外部访问 docker 容器 (-p/-P)3. 无法连接 docker 内 SSH 解决方案 1. 启动 docker 时挂载本地目录 # 将本地 D:/SDK 目录 挂载到 容器里的 /mnt/host 目录中 # 注意:-v /d/SDK:/mnt/host/ 必须放到 IMAGE_ID 前面才行 # …...
:BannerMessagePreference)
【Android 13】使用Android Studio调试系统应用之Settings移植(六):BannerMessagePreference
文章目录 一、篇头二、系列文章2.1 Android 13 系列文章2.2 Android 9 系列文章2.3 Android 11 系列文章三、BannerMessagePreference的移植3.1 新的问题:找不到 R.dimen.settingslib_preferred_minimum_touch_target3.2 问题分析(一)3.2.1 资源定义的位置3.2.2 检查依赖3.2…...

Python 变量
打印输出内容 print(‘rumenle’) print(‘haode’) 缩进需要tab 注释将需要注释的部分开头用# 多行注释 1、用你也可以左键选中我们需要注释的代码,松开,按:Ctrl/,就完成相同效果注释 2、把要注释的内容放到三个引号对里面 …...

ComfyUI如何中文汉化
comfyui中文地址如下: https://github.com/AIGODLIKE/AIGODLIKE-ComfyUI-Translationhttps://github.com/AIGODLIKE/AIGODLIKE-ComfyUI-Translation如何安装? 1. git安装 进入项目目录下的custom_nodes目录下,然后进入控制台,运…...
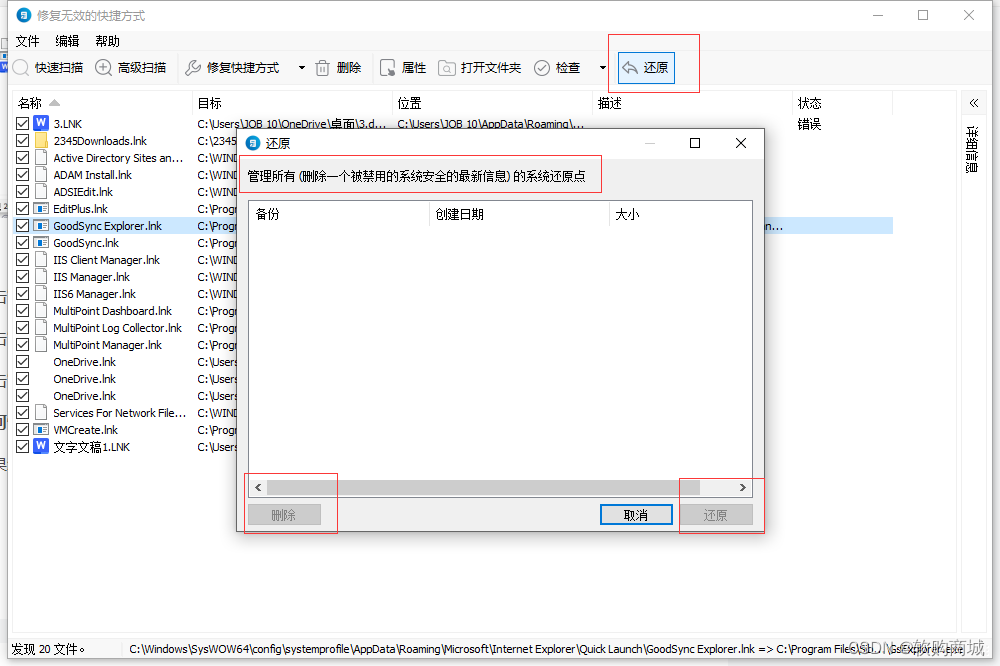
Glary Utilities Pro - 电脑系统优化全面指南:详尽使用教程
软件简介: Glary Utilities Pro 是一款全面的电脑优化工具,它旨在帮助用户提升计算机的性能和稳定性。这款软件提供了多种功能,包括系统清理、优化、修复以及保护。通过一键扫描,它可以识别并清除无用文件、临时数据、注册表错误等…...

1.4分页和排序
排序: -- 分页(limit)和排序(order by) -- 排序:升序ASC,降序DESC -- ORDER BY 通过字段排序,怎么排 -- 查询的结果根据成绩降序,升序 SELECT s.studentno,studentname,sub.subjectname,studentresult FROM student s RIGHT JO…...

Modbus转Profinet,不会编程也能用!轻松快上手!
Modbus转Profinet是一种用于工业自动化领域的通信协议转换器,可以将Modbus协议转换为Profinet协议,实现设备之间的数据交换与通信。这个工具的使用非常简单,即使没有编程经验的人也可以轻松上手。即使不会编程的人也可以轻松快速上手使用Modb…...
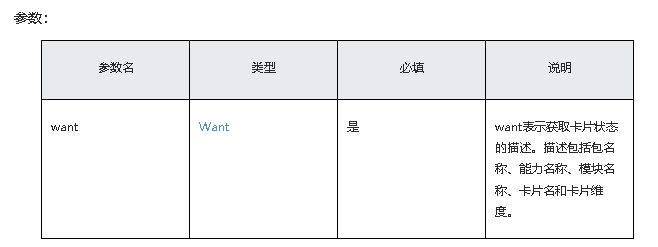
鸿蒙原生应用/元服务开发-Stage模型能力接口(十)下
ohos.app.form.FormExtensionAbility (FormExtensionAbility) 系统能力:SystemCapability.Ability.Form 示例 import FormExtensionAbility from ohos.app.form.FormExtensionAbility; import formBindingData from ohos.app.form.formBindingData; import formP…...

QT QPluginloader 加载失败,出现Unknown error 0x000000c1的问题
最近在学习Qt的插件开发,在加载插件时,一直失败,用如下代码加载并打印错误信息。 QDir dir("./testplugin.dll"); QPluginLoader pluginLoader(dir.absolutePath());//需要绝对路径 pluginLoader.load(); qDebug()<< "…...

众和策略:今年首次!A股罕见一幕
岁末,A股走出了不常见的行情。 这儿指的不单单是指数上涨。今天上午,A股逾3900只个股上涨,昨日逾4400只个股上涨,前天逾3700只个股上涨。据通达信数据显现,这种连续的普涨行情在本年还是头一次。 本年10月底…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

jdbc查询mysql数据库时,出现id顺序错误的情况
我在repository中的查询语句如下所示,即传入一个List<intager>的数据,返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致,会导致返回的id是从小到大排列的,但我不希望这样。 Query("SELECT NEW com…...

【大模型】RankRAG:基于大模型的上下文排序与检索增强生成的统一框架
文章目录 A 论文出处B 背景B.1 背景介绍B.2 问题提出B.3 创新点 C 模型结构C.1 指令微调阶段C.2 排名与生成的总和指令微调阶段C.3 RankRAG推理:检索-重排-生成 D 实验设计E 个人总结 A 论文出处 论文题目:RankRAG:Unifying Context Ranking…...
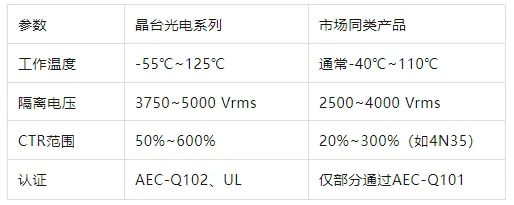
高抗扰度汽车光耦合器的特性
晶台光电推出的125℃光耦合器系列产品(包括KL357NU、KL3H7U和KL817U),专为高温环境下的汽车应用设计,具备以下核心优势和技术特点: 一、技术特性分析 高温稳定性 采用先进的LED技术和优化的IC设计,确保在…...
