[NOIP2012 普及组] 摆花
[NOIP2012 普及组] 摆花
题目描述
小明的花店新开张,为了吸引顾客,他想在花店的门口摆上一排花,共 m m m 盆。通过调查顾客的喜好,小明列出了顾客最喜欢的 n n n 种花,从 1 1 1 到 n n n 标号。为了在门口展出更多种花,规定第 i i i 种花不能超过 a i a_i ai 盆,摆花时同一种花放在一起,且不同种类的花需按标号的从小到大的顺序依次摆列。
试编程计算,一共有多少种不同的摆花方案。
输入格式
第一行包含两个正整数 n n n 和 m m m,中间用一个空格隔开。
第二行有 n n n 个整数,每两个整数之间用一个空格隔开,依次表示 a 1 , a 2 , ⋯ , a n a_1,a_2, \cdots ,a_n a1,a2,⋯,an。
输出格式
一个整数,表示有多少种方案。注意:因为方案数可能很多,请输出方案数对 1 0 6 + 7 10^6+7 106+7 取模的结果。
样例 #1
样例输入 #1
2 4
3 2
样例输出 #1
2
提示
【数据范围】
对于 20 % 20\% 20% 数据,有 0 < n ≤ 8 , 0 < m ≤ 8 , 0 ≤ a i ≤ 8 0<n \le 8,0<m \le 8,0 \le a_i \le 8 0<n≤8,0<m≤8,0≤ai≤8。
对于 50 % 50\% 50% 数据,有 0 < n ≤ 20 , 0 < m ≤ 20 , 0 ≤ a i ≤ 20 0<n \le 20,0<m \le 20,0 \le a_i \le 20 0<n≤20,0<m≤20,0≤ai≤20。
对于 100 % 100\% 100% 数据,有 0 < n ≤ 100 , 0 < m ≤ 100 , 0 ≤ a i ≤ 100 0<n \le 100,0<m \le 100,0 \le a_i \le 100 0<n≤100,0<m≤100,0≤ai≤100。
NOIP 2012 普及组 第三题
#include<bits/stdc++.h>
const int Max=1000007;
using namespace std;
int n,m,a[150],f[150][150];
int main()
{cin>>n>>m;for(int i=1;i<=n;i++)cin>>a[i];for(int i=0;i<=n;i++)f[i][0]=1;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){for(int k=0;k<=min(j,a[i]);k++){f[i][j]=(f[i][j]+f[i-1][j-k])%Max;}}}cout<<f[n][m];return 0;
}
相关文章:

[NOIP2012 普及组] 摆花
[NOIP2012 普及组] 摆花 题目描述 小明的花店新开张,为了吸引顾客,他想在花店的门口摆上一排花,共 m m m 盆。通过调查顾客的喜好,小明列出了顾客最喜欢的 n n n 种花,从 1 1 1 到 n n n 标号。为了在门口展出更…...
系统学习Python——装饰器:函数装饰器-[装饰器状态保持方案:外层作用域和全局变量]
分类目录:《系统学习Python》总目录 闭包函数(带有外围def作用域引用和嵌套的def)常常可以实现相同的效果,特别是用于像被装饰的最初咱数这样的静态数据时。然而在下面这个例子中,我们也需要外层作用域中的一个计数器&…...
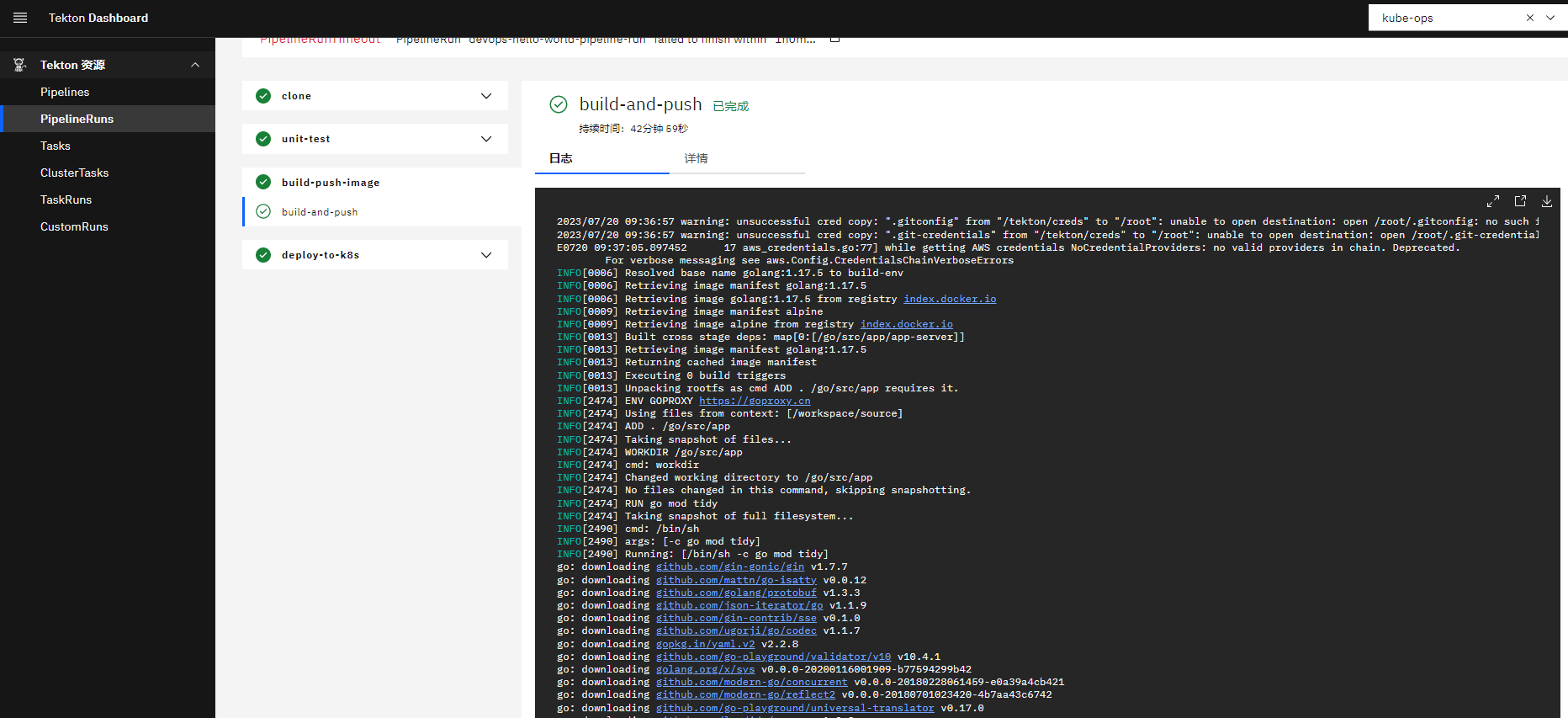
Tekton
一. 概念 Tekton 官网 Github Tekton 是一种用于构建 CI/CD 管道的云原生解决方案,它由提供构建块的 Tekton Pipelines,Tekton 作为 Kubernetes 集群上的扩展安装和运行,包含一组 Kubernetes 自定义资源,这些资源定义了您可以为…...
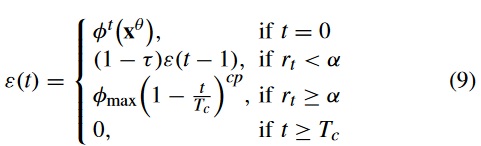
2023,TEVC,A Competitive and Cooperative Swarm Optimizer for Constrained MOP
Abstract 通过元启发式方法求解多目标优化问题( MOPs )得到了广泛的关注。在经典变异算子的基础上,发展了几种改进的变异算子,以及多目标优化进化算法。在这些算子中,竞争群优化算法(CSO)表现出良好的性能。然而,在处理目标空间较…...
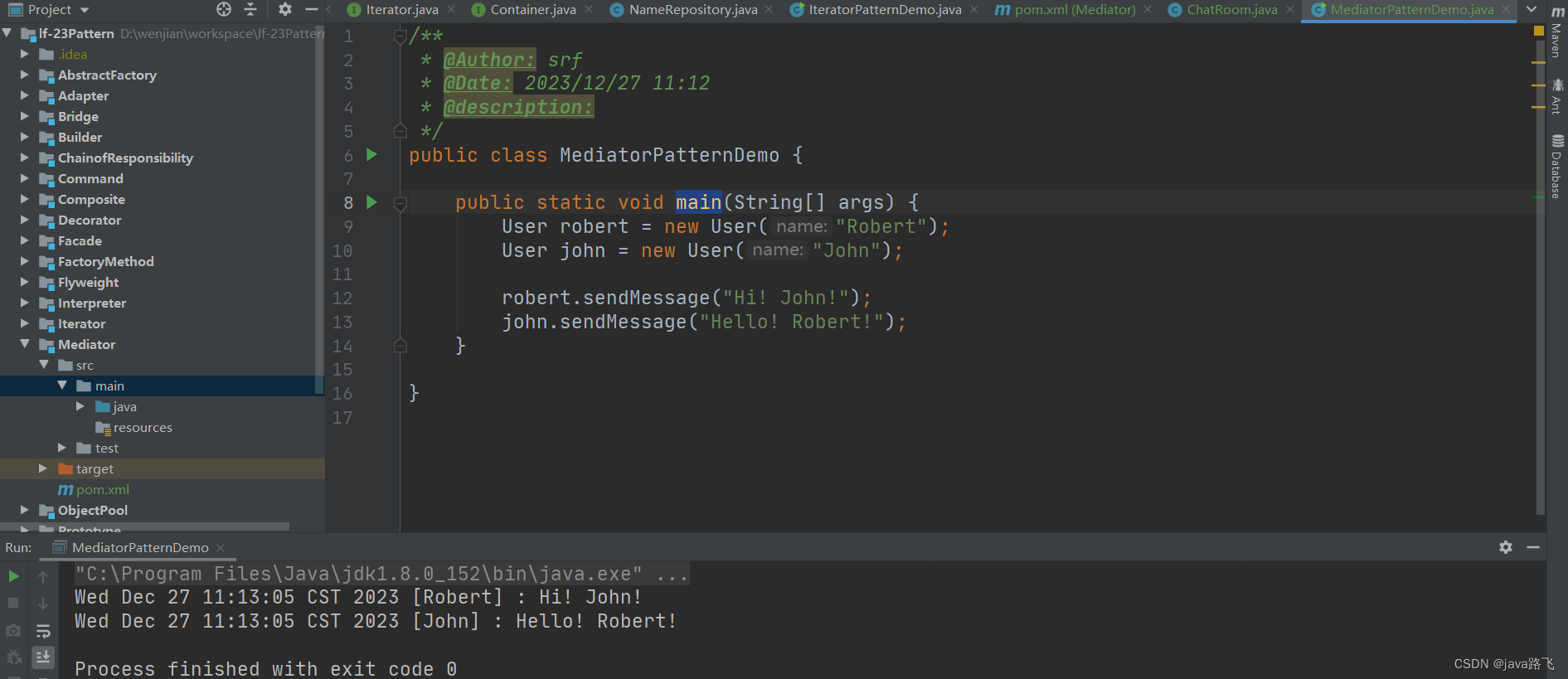
java设计模式学习之【中介者模式】
文章目录 引言中介者模式简介定义与用途实现方式 使用场景优势与劣势在Spring框架中的应用聊天室示例代码地址 引言 想象一下一座忙碌的机场,各种飞机需要起飞、降落,而不同的飞行活动之间必须互不干扰。如果没有一个统一的控制系统,这将是一…...
)
C++三剑客之std::variant(一)
1简介 C17的三剑客分别是std::optional, std::any, std::vairant。今天主要讲std::variant。std::variant的定义如下: template< class... Types > class variant; 类模板 std::variant 表示一个类型安全的联合体(以下称“变化体”)…...

新火种AI|AI正在让汽车成为“消费电子产品”
作者:一号 编辑:小迪 AI正在让汽车产品消费电子化 12月28日,铺垫许久的小米汽车首款产品——小米SU7正式在北京亮相。命里注定要造“电车”的雷军,在台上重磅发布了小米的五大自研核心技术。在车型设计、新能源技术以及智能科技…...

Docker六 | Docker Compose容器编排
目录 Docker Compose 基本概念 使用步骤 常用命令 Docker Compose Docker-Compose是Docker官方的开源项目,负责实现对Docker容器集群的快速编排。Compose可以管理多个Docker容器组成一个应用。 需要定义一个YAML格式的配置文件docker-compose.yml,…...
Oraclelinux部署Oracle服务
采用图形化界面 user用户 oracle用户 #清屏 clear #设置主机名 hostnamectl set-hostname ceshidb sed -i 1,2 s/^/#/ /etc/hosts echo "127.0.0.1 ceshidb" >> /etc/hosts echo "::1 ceshidb" >> /etc/hosts ping -c 5…...
Ubuntu安装K8S(1.28版本,基于containrd)
原文网址:Ubuntu安装K8S(1.28版本,基于containrd)-CSDN博客 简介 本文介绍Ubuntu安装K8S的方法。 官网文档:这里 1.安装K8S 1.让apt支持SSL传输 sudo apt-get update sudo apt-get -y install apt-transport-https ca-certi…...
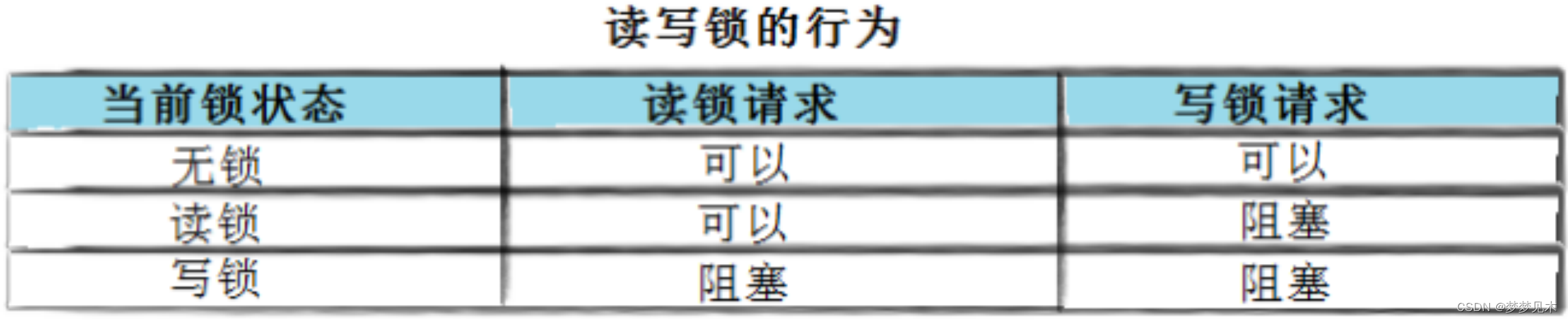
Linux 线程安全 (2)
文章目录 线程同步概念条件变量使用生产消费模型信号量的使用读写锁的使用 Linux 线程安全 (1) 线程同步概念 竞态条件:因为时序问题,而导致程序异常. 饥饿问题:只使用互相锁保证线程安全时,锁资源总被某…...

异或运算^简述
异或运算:^ 两个变量之间异或运算时,其二进制位相同取0,不同取1. 示例:a10 (0b 0000 1010) b3 (0b 0000 0011) a^b9(0b 0000 1001) 据此可以推算异或运算"^"有以下特性: a^a0 (0b 0000 0000)…...

Google Play上架:2023年度总结报告
今天是2023年的最后一个工作日,今天用来总结一下2023年关于谷歌商店上架的相关政策改动和对应的拒审解决方法。 目录 政策更新与改动2023 年 2 月 22 日2023 年 4 月5 日2023 年 7 月 12 日2023 年 10 月 25 日 开发者计划政策拒审邮件内容和解决办法 政策更新与改…...

JAVA进化史: JDK10特性及说明
DK 10(Java Development Kit 10)是Java平台的一个版本,于2018年3月发布。尽管相对于之前的版本,JDK 10的变化较为温和,但仍然引入了一些新特性和改进,以下是其中一些主要特性,并带有相应的示例说…...

第二百三十四回
文章目录 1.概念介绍2.使用方法2.1 NumberPicker2.2 CupertinoPicker 3.示例代码4.内容总结 我们在上一章回中介绍了"如何在任意位置显示PopupMenu"相关的内容,本章回中将介绍如何实现NumberPicker.闲话休提,让我们一起Talk Flutter吧。 1.概念…...
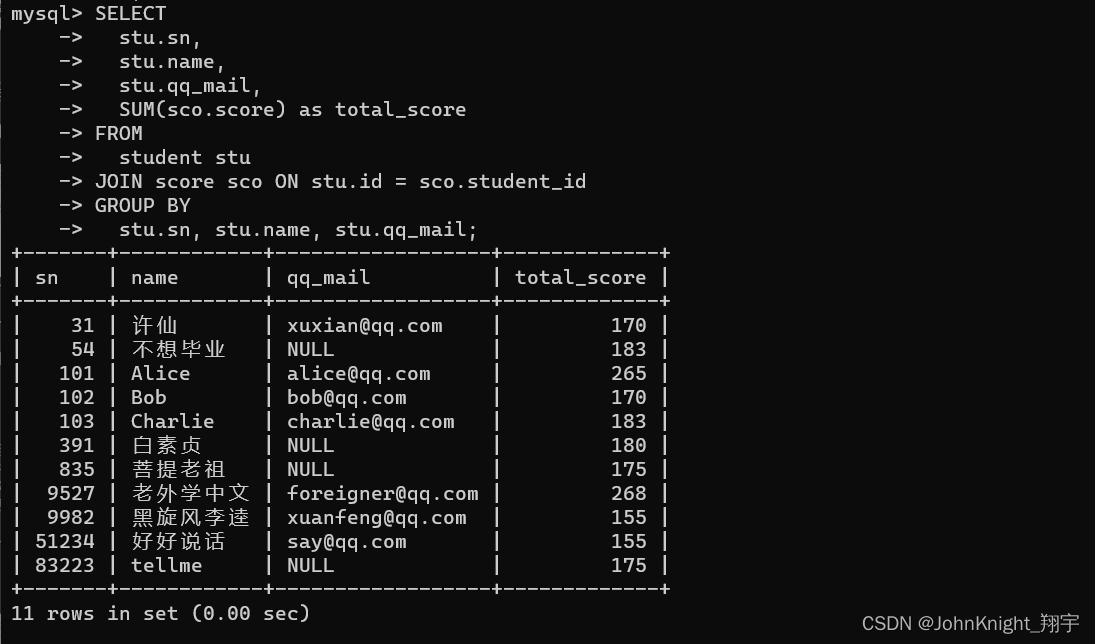
{MySQL} 数据库约束 表的关系 新增删除 修改 查询
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、数据库约束1.1约束类型:1.2 NULL约束1.3unique 唯一约束1.4 DEFAULT:默认值约束1.5 PRIMARY KEY:主键约束1.6 FOREIGN K…...
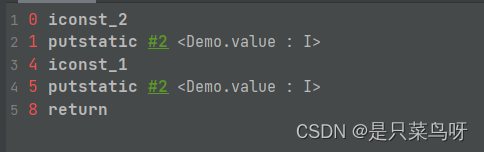
【JVM】虚拟机的组成+字节码文件组成+类的生命周期
什么是JVM? JVM 本质上是一个运行在计算机上的程序,他的职责是运行Java字节码文件。 JVM的功能 1.解释和运行:对字节码文件中的指令实时的解释成机器码让计算机执行。 2.内存管理:自动为对象、方法等分配内存,自动…...

pip 下载太慢的解决办法,pip换国内源,pip换源
用pip安装python包的时候,如果系统没有进行相关设置,则用的源服务器是国外的,在国内访问非常慢,我们需要换成国内的源服务器,pip换源通过如下命令: pip config set global.index-url <源地址> 一、…...
OKCC语音机器人的人机耦合来啦
目前市场上语音机器人的外呼形式基本就分为三种,一种纯AI外呼,第二种也是目前主流的AI外呼转人工。那么第三种也可能是未来的一种趋势,人机耦合,或者也叫人机协同。 那么什么是人机耦合呢? 人机耦合是为真人坐席创造相…...

有序数组的平方
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。 示例 1: 输入:nums [-4,-1,0,3,10] 输出:[0,1,9,16,100] 解释:平方后,数组变为 …...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...
