把数组里面数值排成最小的数
问题描述:输入一个正整数数组,将它们连接起来排成一个数,输出能排出的所有数字中最小的一个。例如输入数组{12, 567},则输出这两个能排成的最小数字12567。请给出解决问题的算法,并证明该算法。
思路:先将整数数组转为字符串数组,然后字符串数组进行排序,最后依次输出字符串数组即可。这里注意的是字符串的比较函数需要重新定义,不是比较a和b,而是比较ab与 ba。如果ab < ba,则a < b;如果ab > ba,则a > b;如果ab = ba,则a = b。比较函数的定义是本解决方案的关键。
证明:为什么这样排个序就可以了呢?简单证明一下。根据算法,如果a < b,那么a排在b前面,否则b排在a前面。可利用反证法,假设排成的最小数字为xxxxxx,并且至少存在一对字符串满足这个关系:a > b,但是在组成的数字中a排在b前面。根据a和b出现的位置,分三种情况考虑:
(1)xxxxab,用ba代替ab可以得到xxxxba,这个数字是小于xxxxab,与假设矛盾。因此排成的最小数字中,不存在上述假设的关系。
(2)abxxxx,用ba代替ab可以得到baxxxx,这个数字是小于abxxxx,与假设矛盾。因此排成的最小数字中,不存在上述假设的关系。
(3)axxxxb,这一步证明麻烦了一点。可以将中间部分看成一个整体ayb,则有ay < ya,yb < by成立。将ay和by表示成10进制数字形式,则有下述关系式,这里a,y,b的位数分别为n,m,k。
关系1: ay < ya => a * 10^m + y < y * 10^n + a => a * 10^m - a < y * 10^n - y => a( 10^m - 1)/( 10^n - 1) < y
关系2: yb < by => y * 10^k + b < b * 10^m + y => y * 10^k - y < b * 10^m - b => y < b( 10^m -1)/( 10^k -1)
关系3: a( 10^m - 1)/( 10^n - 1) < y < b( 10^m -1)/( 10^k -1) => a/( 10^n - 1)< b/( 10^k -1) => a*10^k - a < b * 10^n - b =>a*10^k + b < b * 10^n + a => a < b
这与假设a > b矛盾。因此排成的最小数字中,不存在上述假设的关系。
综上所述,得出假设不成立,从而得出结论:对于排成的最小数字,不存在满足下述关系的一对字符串:a > b,但是在组成的数字中a出现在b的前面。从而得出算法是正确的。
参考代码:
//重新定义比较函数对象
struct compare
{bool operator() (const string &src1, const string &src2){string s1 = src1 + src2;string s2 = src2 + src1;return s1 < s2; //升序排列,如果改为s1 > s2则为逆序排列}
};
//函数功能 : 把数组排成最小的数
//函数参数 : pArray为数组,num为数组元素个数
//返回值 : 无
void ComArrayMin(int *pArray, int num)
{int i;string *pStrArray = new string[num];for(i = 0; i < num; i++) //将数字转换为字符串{ stringstream stream;stream<<pArray[i];stream>>pStrArray[i];}sort(pStrArray, pStrArray + num, compare()); //字符串数组排序for(i = 0; i < num; i++) //打印字符串数组cout<<pStrArray[i];cout<<endl;delete [] pStrArray;
}相关文章:

把数组里面数值排成最小的数
问题描述:输入一个正整数数组,将它们连接起来排成一个数,输出能排出的所有数字中最小的一个。例如输入数组{12, 567},则输出这两个能排成的最小数字12567。请给出解决问题的算法,并证明该算法。 思路:先将…...
云his系统源码 SaaS应用 基于Angular+Nginx+Java+Spring开发
云his系统源码 SaaS应用 功能易扩 统一对外接口管理 一、系统概述: 本套云HIS系统采用主流成熟技术开发,软件结构简洁、代码规范易阅读,SaaS应用,全浏览器访问前后端分离,多服务协同,服务可拆分ÿ…...

小红书场景营销怎么做?场景营销主要模式有哪些
小红书作为新兴媒体领域的佼佼者,凭借着生动,直观,代入感等元素的分享推荐收揽了巨额的流量。但是,随着时代的脚步逐渐加快,发展和变革随之涌来,传统的营销已经无法满足。所以场景营销就出现了。今天就来和…...

c++基础——数组
数组数组是存放相同类型对象的容器,数组中存放的对象没有名字,而是要通过其所在的位置访问。数组的大小是固定的,不能随意改变数组的长度。定义数组数组的声明形如 a[b],其中,a 是数组的名字,b 是数组中元素…...
odoo15 登录界面的标题自定义
odoo15 登录界面的标题自定义 原代码中查询:<title>Odoo<title> <html> <head><meta http-equiv="content-type" content="text/html; charset=utf-8" /><title>Odoo</title><link rel="shortcut icon…...

【内网服务通过跳板机和公网通信】花生壳内网穿透+Nginx内网转发+mqtt服务搭建
问题:服务不能暴露公网 客户的主机不能连外网,服务MQTT服务部署在内网。记做:p1 (computer 1)堡垒机(跳板机)可以连外网,内网IP 和 MQTT服务在同一个网段。记做:p2 (computer 2)对他人而言&…...

【多线程常见面试题】
谈谈 volatile关键字的用法? volatile能够保证内存可见性,强制从主内存中读取数据,此时如果有其他线程修改被volatile修饰的变量,可以第一时间读取到最新的值 Java多线程是如何实现数据共享的? JVM把内存分成了这几个区域: 方法区,堆区,栈区,程序计数器; 其中堆区…...

深度剖析指针(下)——“C”
各位CSDN的uu们你们好呀,今天小雅兰的内容还是我们的指针呀,上两篇博客我们基本上已经把知识点过了一遍,这篇博客就让小雅兰来带大家看一些和指针有关的题目吧,现在,就让我们进入指针的世界吧 复习: 数组和…...

爬虫与反爬虫技术简介
互联网的大数据时代的来临,网络爬虫也成了互联网中一个重要行业,它是一种自动获取网页数据信息的爬虫程序,是网站搜索引擎的重要组成部分。通过爬虫,可以获取自己想要的相关数据信息,让爬虫协助自己的工作,…...

Pag的2D渲染执行流程
Pag的渲染 背景 根据Pag文章里面说的,Pag之前长时间使用的Skia库作为底层渲染引擎。但由于Skia库体积过大,为了保证通用型(比如兼容CPU渲染)做了很多额外的事情。所以Pag的工程师们自己实现了一套2D图形框架替换掉Skiaÿ…...

k8s 概念说明,k8s面试题
什么是Kubernetes? Kubernetes是一种开源容器编排系统,可自动化应用程序的部署、扩展和管理。 Kubernetes 中的 Master 组件有哪些? Kubernetes 中的 Master 组件包括 API Server、etcd、Scheduler 和 Controller Manager。 Kubernetes 中的…...

Docker--(四)--搭建私有仓库(registry、harbor)
私有仓库----registry官方提供registry仓库管理(推送、删除、下载)私有仓库----harbor私有镜像仓库1.私有仓库----registry官方提供 Docker hub官方已提供容器镜像registry,用于搭建私有仓库 1.1 镜像拉取、运行、查看信息、测试 (一) 拉取镜像 # dock…...

Invalid <url-pattern> [sso.action] in filter mapping
Tomcat 8.5.86版本启动web项目报错Caused by: java.lang.IllegalArgumentException: Invalid <url-pattern> [sso.action] in filter mapping 查看项目的web.xml文件相关片段 <filter-mapping><filter-name>SSOFilter</filter-name><url-pattern&g…...

【11】linux命令每日分享——useradd添加用户
大家好,这里是sdust-vrlab,Linux是一种免费使用和自由传播的类UNIX操作系统,Linux的基本思想有两点:一切都是文件;每个文件都有确定的用途;linux涉及到IT行业的方方面面,在我们日常的学习中&…...
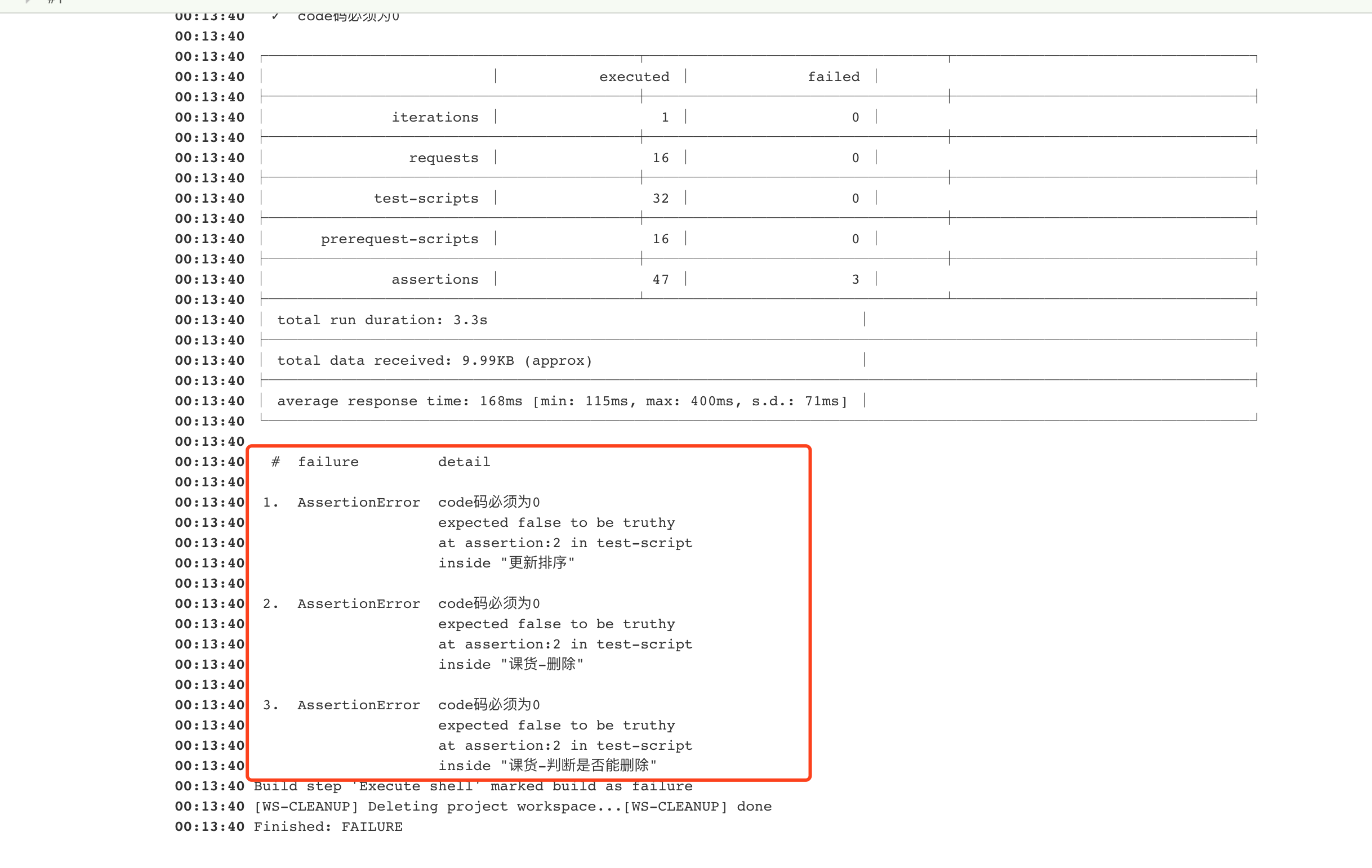
Newman+Jenkins实现接口自动化测试
一、是什么Newman Newman就是纽曼手机这个经典牌子,哈哈,开玩笑啦。。。别当真,简单地说Newman就是命令行版的Postman,查看官网地址。 Newman可以使用Postman导出的collection文件直接在命令行运行,把Postman界面化运…...

MySQL:事务+@Transactional注解
事务 本章从了解为什么需要事务到讲述事务的四大特性和概念,最后讲述MySQL中的事务使用语法以及一些需要注意的性质。 再额外讲述一点Springboot中Transactional注解的使用。 1.为什么需要事务? 我们以用户转账为例,假设用户A和用户B的银行账…...
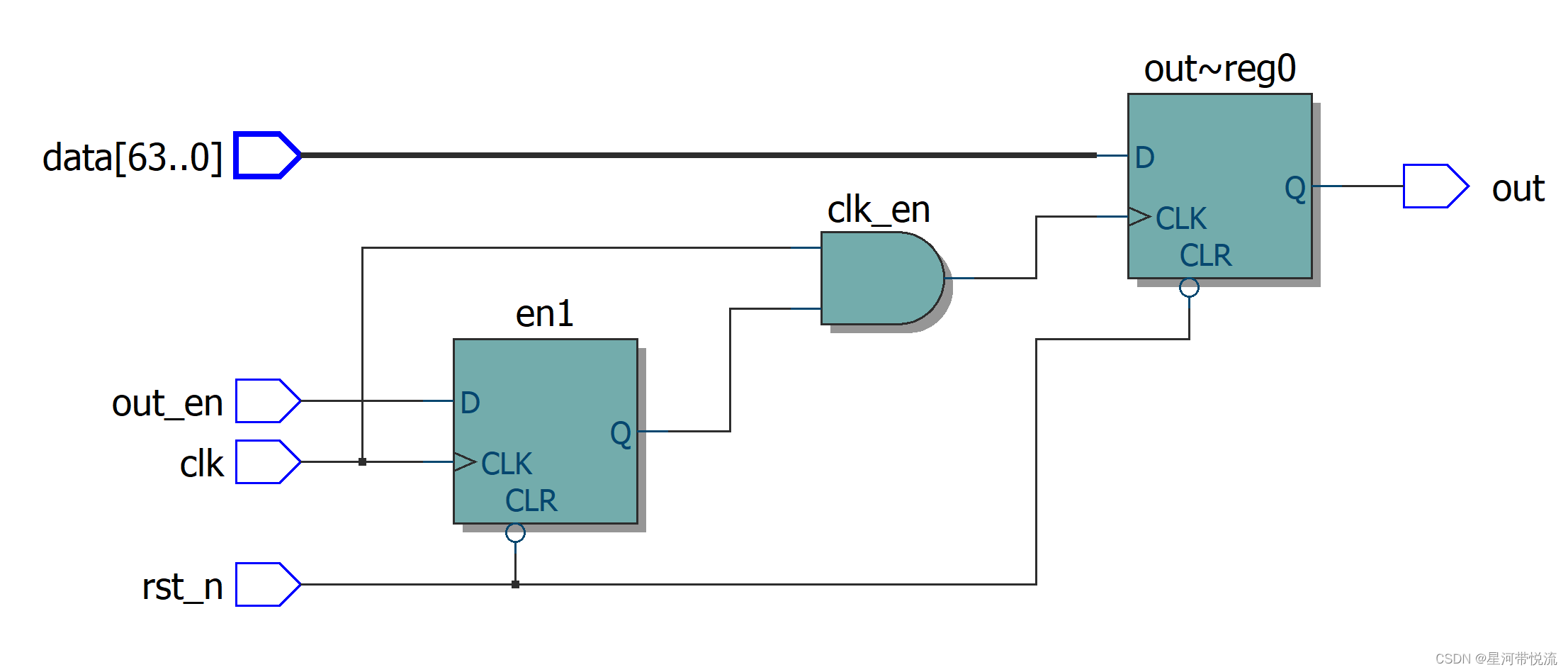
数字IC手撕代码--低功耗设计 Clock Gating
背景介绍芯片功耗组成中,有高达 40%甚至更多是由时钟树消耗掉的。这个结果的原因也很直观,因 为这些时钟树在系统中具有最高的切换频率,而且有很多时钟 buffer,而且为了最小化时钟 延时,它们通常具有很高的驱动强度。 …...

易基因|m6A RNA甲基化研究的数据挖掘思路:干货系列
大家好,这里是专注表观组学十余年,领跑多组学科研服务的易基因。关于m6A甲基化研究思路(1)整体把握m6A甲基化图谱特征:m6A peak数量变化、m6A修饰基因数量变化、单个基因m6A peak数量分析、m6A peak在基因元件上的分布…...

【微信小程序】-- 页面配置(十八)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...

玩好 StarRocks,大厂 offer 接不完!|字节跳动、小红书、京东物流、唯品会、腾讯音乐要的就是你!
求职黄金季即将到来,你准备好迎接你的 dream offer 了吗?StarRocks 自创立以来,一直主张为用户创造极速统一的数据分析新范式,让数据驱动创新,而优秀的大数据人才对推动创新有着至关重要的作用。因此,我们推…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...
