CF1574C Slay the Dragon 题解
CF1574C Slay the Dragon 题解
- 题目
- 链接
- 字面描述
- 题面翻译
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 代码实现
题目
链接
https://www.luogu.com.cn/problem/CF1574C
字面描述
题面翻译
给定长度为 nnn 的序列 aaa,mmm 次询问,每次询问包含两个参数 x,yx,yx,y,你可以给序列任意位置 +1+1+1,最后你需要找出一个位置 ppp ,满足
- ap≥xa_p\ge xap≥x
- ∑i=1nai[i≠p]≥y\displaystyle\sum_{i=1}^n a_i[i\not= p] \ge yi=1∑nai[i=p]≥y
最小化 +1+1+1 次数,输出其次数。
限制:2≤n≤2×105,1≤m≤2×105,1≤ai,x≤1012,1≤y≤10182\le n\le2\times 10^5,1\le m\le 2\times10^5,1\le a_i,x\le 10^{12},1\le y\le 10^{18}2≤n≤2×105,1≤m≤2×105,1≤ai,x≤1012,1≤y≤1018
Translated by 飞丞
题目描述
Recently, Petya learned about a new game “Slay the Dragon”. As the name suggests, the player will have to fight with dragons. To defeat a dragon, you have to kill it and defend your castle. To do this, the player has a squad of $ n $ heroes, the strength of the $ i $ -th hero is equal to $ a_i $ .
According to the rules of the game, exactly one hero should go kill the dragon, all the others will defend the castle. If the dragon’s defense is equal to $ x $ , then you have to send a hero with a strength of at least $ x $ to kill it. If the dragon’s attack power is $ y $ , then the total strength of the heroes defending the castle should be at least $ y $ .
The player can increase the strength of any hero by $ 1 $ for one gold coin. This operation can be done any number of times.
There are $ m $ dragons in the game, the $ i $ -th of them has defense equal to $ x_i $ and attack power equal to $ y_i $ . Petya was wondering what is the minimum number of coins he needs to spend to defeat the $ i $ -th dragon.
Note that the task is solved independently for each dragon (improvements are not saved).
输入格式
The first line contains a single integer $ n $ ( $ 2 \le n \le 2 \cdot 10^5 $ ) — number of heroes.
The second line contains $ n $ integers $ a_1, a_2, \dots, a_n $ ( $ 1 \le a_i \le 10^{12} $ ), where $ a_i $ is the strength of the $ i $ -th hero.
The third line contains a single integer $ m $ ( $ 1 \le m \le 2 \cdot 10^5 $ ) — the number of dragons.
The next $ m $ lines contain two integers each, $ x_i $ and $ y_i $ ( $ 1 \le x_i \le 10^{12}; 1 \le y_i \le 10^{18} $ ) — defense and attack power of the $ i $ -th dragon.
输出格式
Print $ m $ lines, $ i $ -th of which contains a single integer — the minimum number of coins that should be spent to defeat the $ i $ -th dragon.
样例 #1
样例输入 #1
4
3 6 2 3
5
3 12
7 9
4 14
1 10
8 7
样例输出 #1
1
2
4
0
2
提示
To defeat the first dragon, you can increase the strength of the third hero by $ 1 $ , then the strength of the heroes will be equal to $ [3, 6, 3, 3] $ . To kill the dragon, you can choose the first hero.
To defeat the second dragon, you can increase the forces of the second and third heroes by $ 1 $ , then the strength of the heroes will be equal to $ [3, 7, 3, 3] $ . To kill the dragon, you can choose a second hero.
To defeat the third dragon, you can increase the strength of all the heroes by $ 1 $ , then the strength of the heroes will be equal to $ [4, 7, 3, 4] $ . To kill the dragon, you can choose a fourth hero.
To defeat the fourth dragon, you don’t need to improve the heroes and choose a third hero to kill the dragon.
To defeat the fifth dragon, you can increase the strength of the second hero by $ 2 $ , then the strength of the heroes will be equal to $ [3, 8, 2, 3] $ . To kill the dragon, you can choose a second hero.
代码实现
#include<bits/stdc++.h>
#define ll long long
using namespace std;const int maxn=2e5+10;
int n,m;
ll tot;
ll a[maxn];
int main(){scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%lld",&a[i]);tot+=a[i];}sort(a+1,a+n+1);scanf("%d",&m);while(m--){ll x,y;scanf("%lld%lld",&x,&y);if(tot<x+y){if(a[1]>x){printf("%lld\n",y-(tot-a[1]));continue;}int l=1,r=n;while(l<=r){int mid=l+r>>1;if(a[mid]>x)r=mid-1;else if(a[mid]<x)l=mid+1;else break;}int op=l+r>>1;if(y<=tot-a[op])printf("%lld\n",x-a[op]);else printf("%lld\n",x-a[op]+y-(tot-a[op]));continue;}else{if(a[1]>x){if(y>tot-a[1])printf("%lld\n",y-(tot-a[1]));else printf("0\n");continue;}int l=1,r=n;while(l<=r){int mid=l+r>>1;if(a[mid]>x)r=mid-1;else if(a[mid]<x)l=mid+1;else break;}int op=l+r>>1;int op1=op+1;if(tot==x+y){if(op1<=n)printf("%lld\n",min(x-a[op],a[op1]-x));else printf("%lld\n",x-a[op]);}else{if(y<=tot-a[op1]){if(op1<=n)printf("0\n");else printf("%lld\n",x-a[op]);}else {if(op1<=n)printf("%lld\n",min(x-a[op],y-(tot-a[op1])));else printf("%lld\n",x-a[op]);}}}}return 0;
}
相关文章:

CF1574C Slay the Dragon 题解
CF1574C Slay the Dragon 题解题目链接字面描述题面翻译题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示代码实现题目 链接 https://www.luogu.com.cn/problem/CF1574C 字面描述 题面翻译 给定长度为 nnn 的序列 aaa,mmm 次询问,每次询…...
创建Django项目
创建Django项目 步骤 创建Django项目 django-admin startproject name 创建子应用 python manager.py startapp name创建工程 在使用Flask框架时,项目工程目录的组织与创建是需要我们自己手动创建完成的。 在django中,项目工程目录可以借助django提供…...
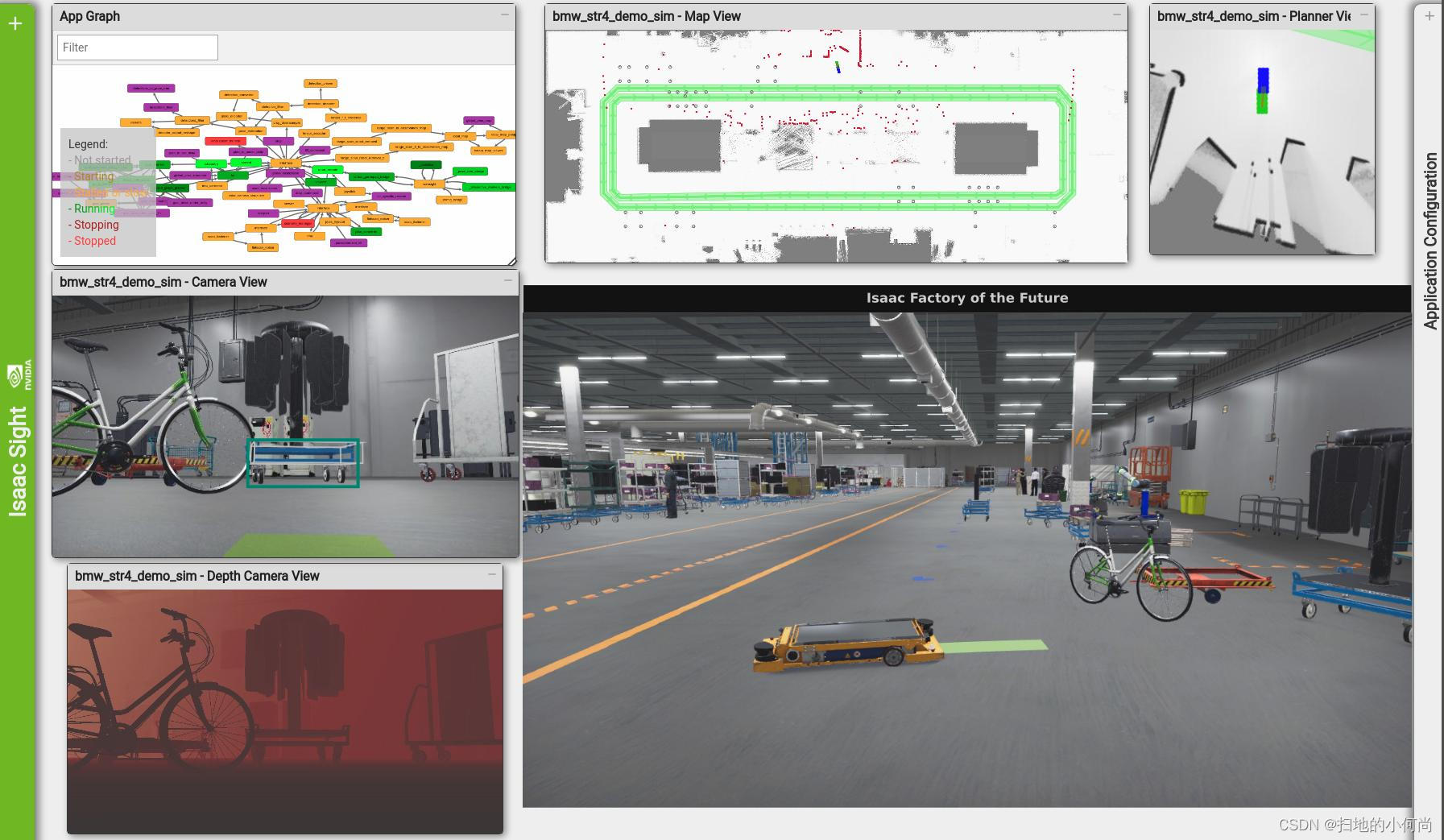
CUDA中的统一内存
文章目录1. Unified Memory Introduction1.1. System Requirements1.2. Simplifying GPU Programming1.3. Data Migration and Coherency1.4. GPU Memory Oversubscription1.5. Multi-GPU1.6. System Allocator1.7. Hardware Coherency1.8. Access Counters2. Programming Mode…...

利用机器学习(mediapipe)进行人脸468点的3D坐标检测--视频实时检测
上期文章,我们分享了人脸468点的3D坐标检测的图片检测代码实现过程,我们我们介绍一下如何在实时视频中,进行人脸468点的坐标检测。 import cv2 import mediapipe as mp mp_drawing = mp.solutions.drawing_utils mp_face_mesh = mp.solutions.face_mesh face_mesh = mp_fac…...
事务基础知识与执行计划
事务基础知识 数据库事务的概念 数据库事务是什么? 事务是一组原子性的SQL操作。事务由事务开始与事务结束之间执行的全部数据库操作组成。A(原子性)、(C一致性)、I(隔离性)、D(持久…...
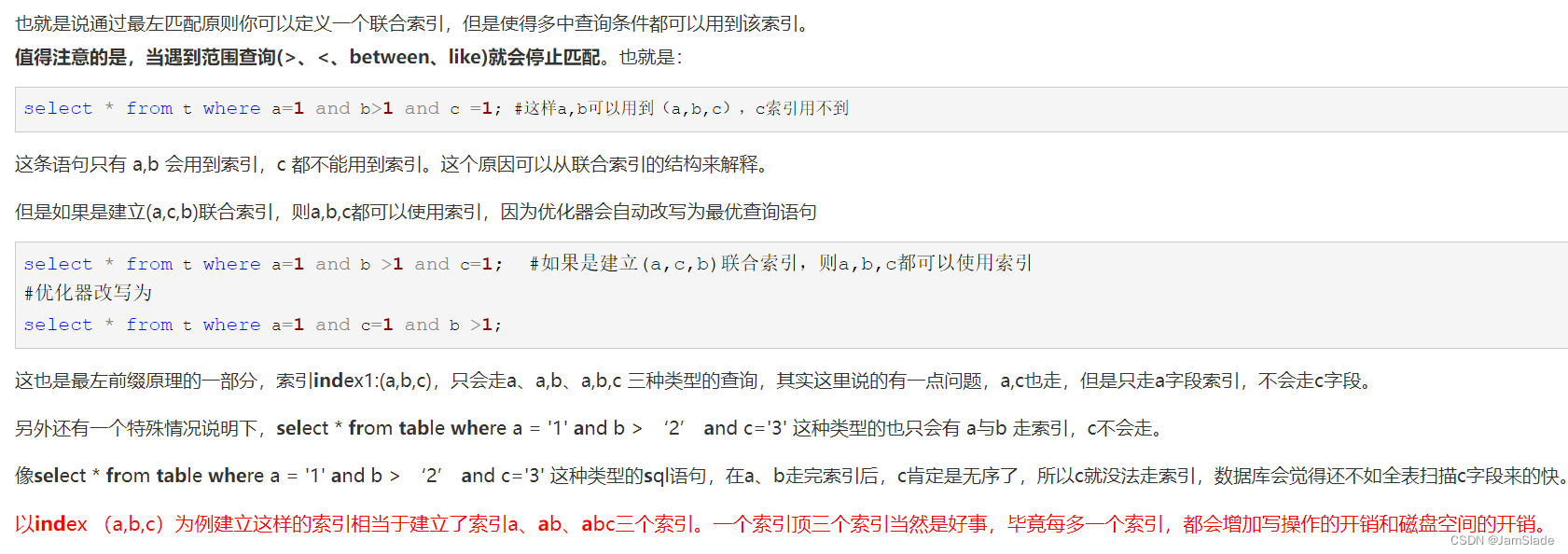
数据库实践LAB大纲 06 INDEX
索引 索引是一个列表 —— 若干列集合和这些值的记录在数据表存储位置的物理地址 作用 加快检索速度唯一性索引 —— 保障数据唯一性加速表的连接分组和排序进行检索的时候 —— 减少时间消耗 一般建立原则 经常查询的数据主键外键连接字段排序字段少涉及、重复值多的字段…...

网络安全实验室6.解密关
6.解密关 1.以管理员身份登录系统 url:http://lab1.xseclab.com/password1_dc178aa12e73cfc184676a4100e07dac/index.php 进入网站点击忘记密码的链接,进入到重置密码的模块 输入aaa,点击抓包,发送到重放模块go 查看返回的链接…...
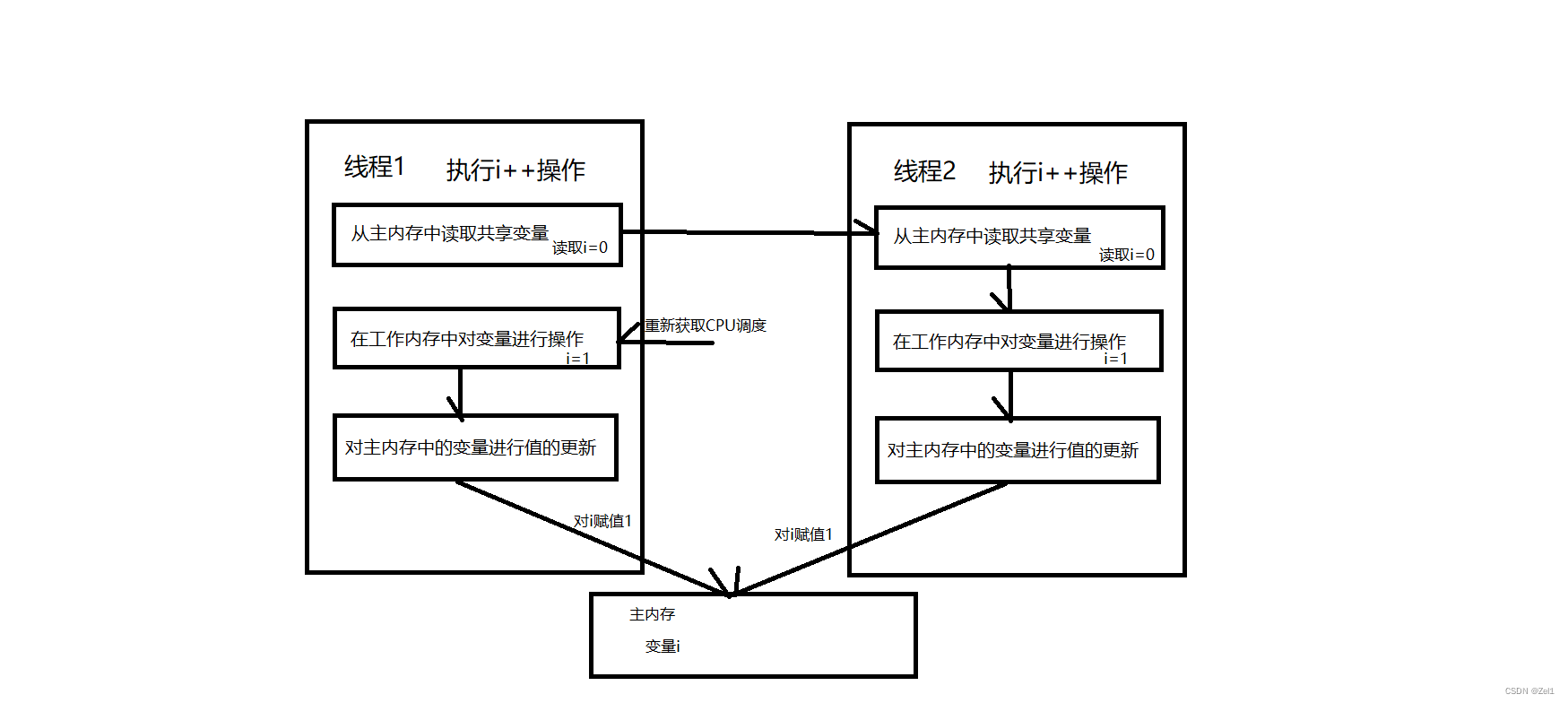
了解并发编程
并发与并行的概念: 并发:一段时间内(假设只有一个CPU)执行多个线程,多个线程时按顺序执行 并行:同个时间点上,多个线程同时执行(多个CPU) 什么是并发编程? 在现代互联网的应用中,会出现多个请求同时对共享资源的访问情况,例如在买票,秒杀与抢购的场景中 此时就会出现线程安…...

(C语言)程序环境和预处理
问:1. 什么是C语言的源代码?2. 由于计算机只认识什么?因此它只能接收与执行什么?也就是什么?3. 在ANSI C的任何一种实现中,存在哪两个不同的环境?在这两种环境里面分别干什么事情?4.…...
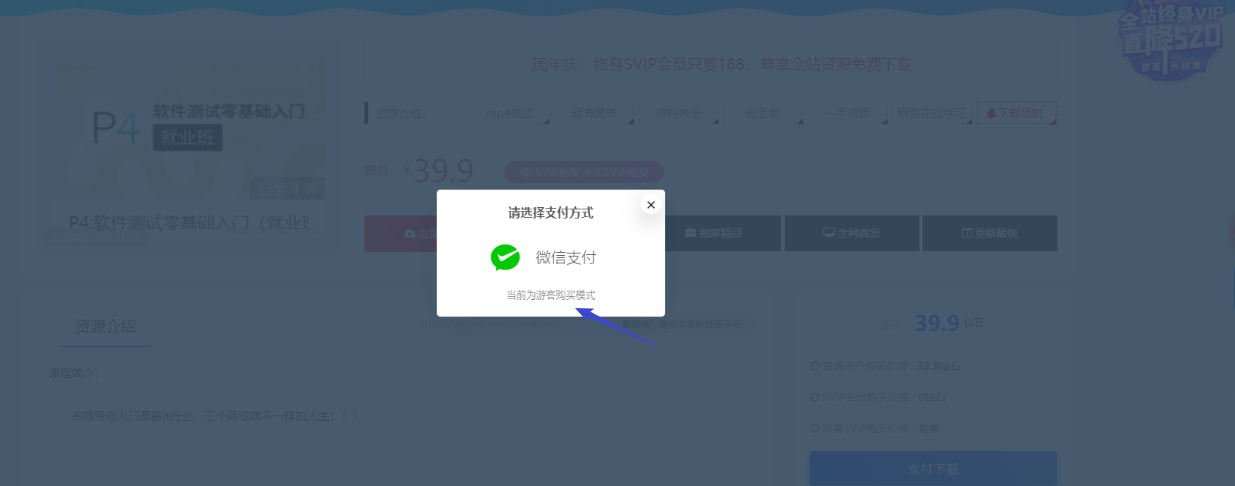
RiProV2主题美化增加支付页底部提示语ritheme主题美化
美化背景 默认的RiProV2主题在支付提示页,是没有这一行提示的 希望增加根据用户类别,未登录用户购买时提示:当前为游客模式购买。或者其他提示,提示用户未登录购买不保存购买记录等。 索引关键字:ritheme主题美化之增加支付页底部提示语,RiProV2主题美化增加支付页底部提…...

2022年文章分类整理
文章目录JetPack系列Kotlin相关View相关多线程相关存储相关Gradle相关动画相关其他2022年公众号(名字:代码说)发表的文章,分类整理一下,方便阅读!2023,继续加油,共勉!JetPack系列 Android Jetp…...

蓝牙设备中的Device UUID 与 Service UUID
Device UUID也可以被称作为DeviceID。 Android 设备上扫描获取到的 deviceId 为外围设备的 MAC 地址,相对固定。 iOS 设备上扫描获取到的 deviceId 是系统根据外围设备 MAC 地址及发现设备的时间生成的 UUID,是设备上的Core Bluetooth为该设备分配的标识…...
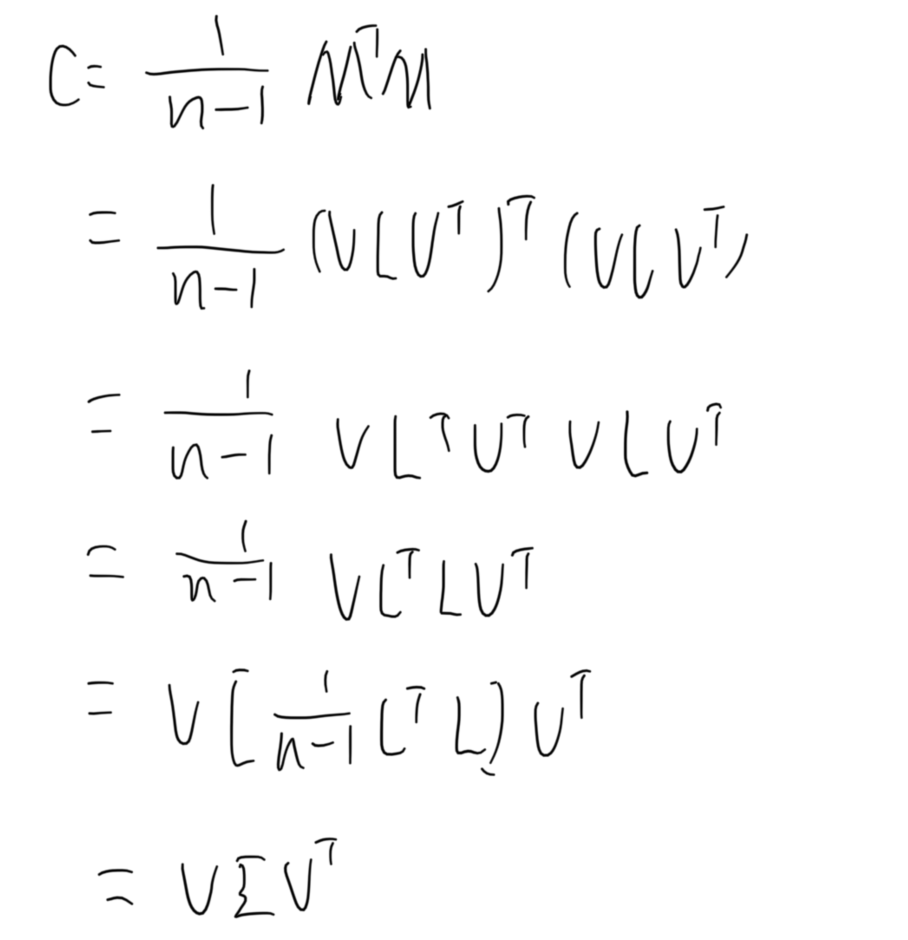
【学习记录】PCA主成分分析 SVD奇异值分解
在看MSC-VO代码的过程中,大量出现了奇异值分解的内容,本身对这部分了解不多,这里补一下课,参考b站up主小旭学长的视频,链接为:PCA主成分分析和SVD主成分分析 PCA主成分分析 PCA根本目的在于让数据在损失尽…...
用 Python 调用 GPT-3 API
用 Python 调用 GPT-3 API GPT-3 是去年由 Open AI 推出的语言机器学习模型。它因其能够写作、写歌、写诗,甚至写代码而获得了广泛的媒体关注!该工具免费使用,只需要注册一个电子邮件即可。 GPT-3 是一种叫 transformer 的机器学习模型。具体…...

类和对象实操之【日期类】
✨个人主页: Yohifo 🎉所属专栏: C修行之路 🎊每篇一句: 图片来源 The pessimist complains about the wind; the optimist expects it to change; the realist adjusts the sails. 悲观主义者抱怨风;乐观主义者期望它…...
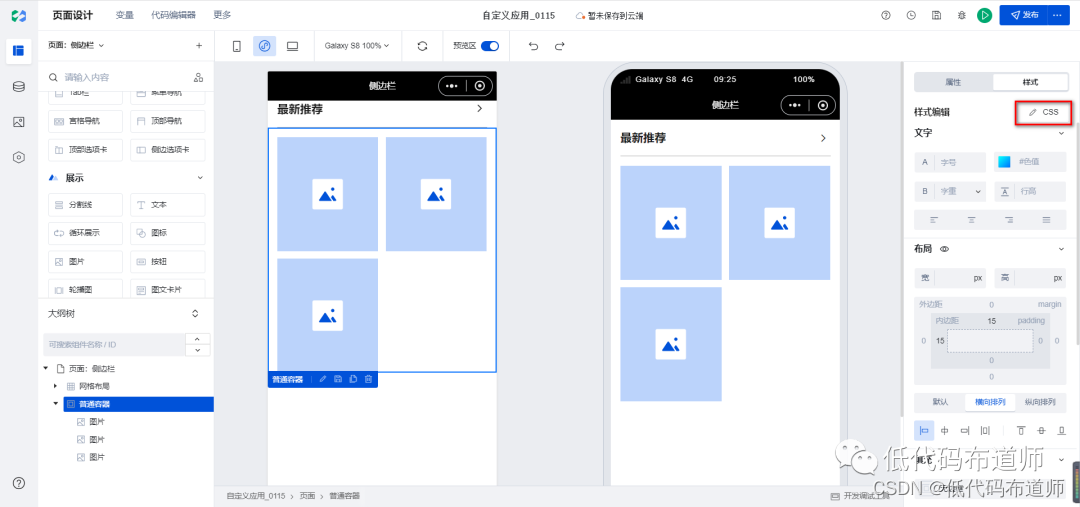
微搭中如何实现弹性布局
我们在实际开发中经常可能会有一些社交的场景,比如开发一个类似朋友圈九宫格图片展示的功能。因为图片的数量不确定,所以需要实现图片的从左到右顺序排列。 在微搭中可以以可视化的方式设置样式。但是对于我们这类特殊需求,只用可视化设置显…...

九龙证券|外资强势出手!这只科创板百元股,被疯狂加仓
本周,北上资金净买入29.32亿元,连续第13周加仓A股。分商场看,北上资金加仓重点倾向于沪市的白马蓝筹股,沪股通取得50.34亿元,深股通则被净卖出21.02亿元。 食品饮料本周取得逾23亿元的增持,居职业首位&…...
)
51单片机最强模块化封装(4)
文章目录 前言一、创建key文件,添加key文件路径二、key文件编写三、模块化测试总结前言 本篇文章将为大家带来按键的模块化封装,这里使用到了三行按键使得我们的代码更加简便。 按键原理:独立按键 一、创建key文件,添加key文件路径 这里的操作就不过多解释了,大家自行看…...
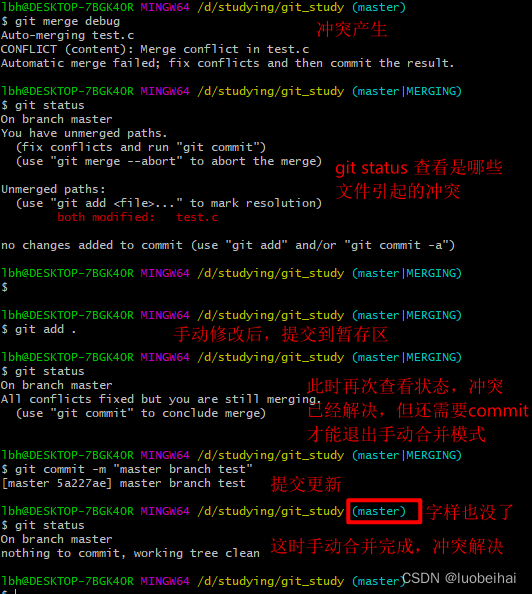
五、Git本地仓库基本操作——分支管理
1. 什么是分支? master分支 我们在初始化git仓库的时候,会默认创建一个master分支,HEAD指针这时就会默认执行master分支。当我们在master分支提交(commit)了更新之后,master分支就会指向当前当前最新的co…...

vscode搭建python Django网站开发环境
这里使用pip安装的方式,打开命令行,输入执行: pip install django2.2这里选择安装2.2版本是因为是新的lts版本,长期支持稳定版。 接下来再安装pillow,Django底层一部分是基于pillow进行的。 pip install pillowpylint…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
