【学习记录】PCA主成分分析 SVD奇异值分解
在看MSC-VO代码的过程中,大量出现了奇异值分解的内容,本身对这部分了解不多,这里补一下课,参考b站up主小旭学长的视频,链接为:PCA主成分分析和SVD主成分分析
PCA主成分分析
PCA根本目的在于让数据在损失尽可能小的前提下,降低数据的维度。比如将三维数据降低到二维,那么就是要在空间中找一个平面,让3d点在2d平面上的投影尽可能保持原来3d空间下的分布。将这个概念推广一下,PCA的任务也就是找一个新的坐标系,让原数据在新坐标系下的投影损失尽可能小,而这个新的坐标系的寻找方法,我们就要依赖于方差这一概念。这里我们可以这样去理解,方差衡量的是数据的密集程度,方差小意味着这一大堆数据几乎就是集中在一小撮,这样必然会导致数据的差异性变得很模糊,因此我们在进行降维时,需要寻找的坐标系最好是方差尽可能大的,从而能让数据降维后分布尽量分散。因此这里我们要寻找的这个坐标系,就是原数据中方差最大的方向。

在进行坐标系的寻找之前,我们需要对原始数据做一个中心化的操作,也就是将坐标原点移动到数据的分布中心,这主要是为了更好地寻找方差最大的方向。移动到中心后,就需要进行一系列的推导,这里我们假定最后的处理结果数据符合高斯分布,根据线性代数中数据的拉伸和旋转的写法,拉伸等于左乘一个对角阵,旋转等于左乘一个三角函数构成的矩阵,数据的处理前后本身就可以用旋转和拉伸来表示。
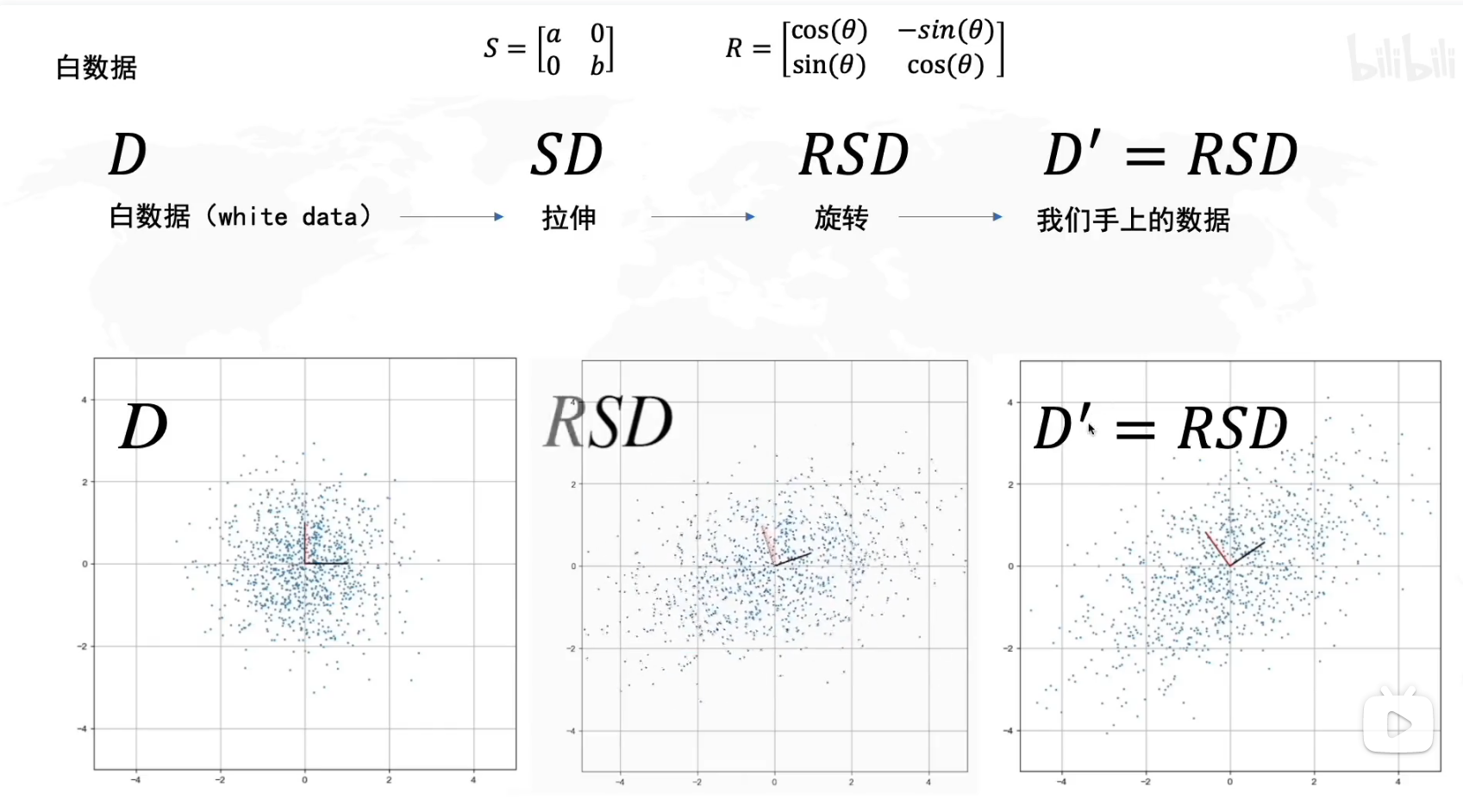
上图描述的是原始数据和最终结果之间通过旋转和拉伸的转换关系,在这个问题中,我们并不知道旋转和拉伸的幅度,所以问题变为如何求R和S。在求R和S的过程中,我们需要利用协方差矩阵COV,协方差用于表示两个变量在变化过程中的关联关系,协方差为正表示两个量是正相关,反之为负相关,如果为零则表示两个量相互无关。根据协方差矩阵的定义,我们可以得到下面的化简公式:
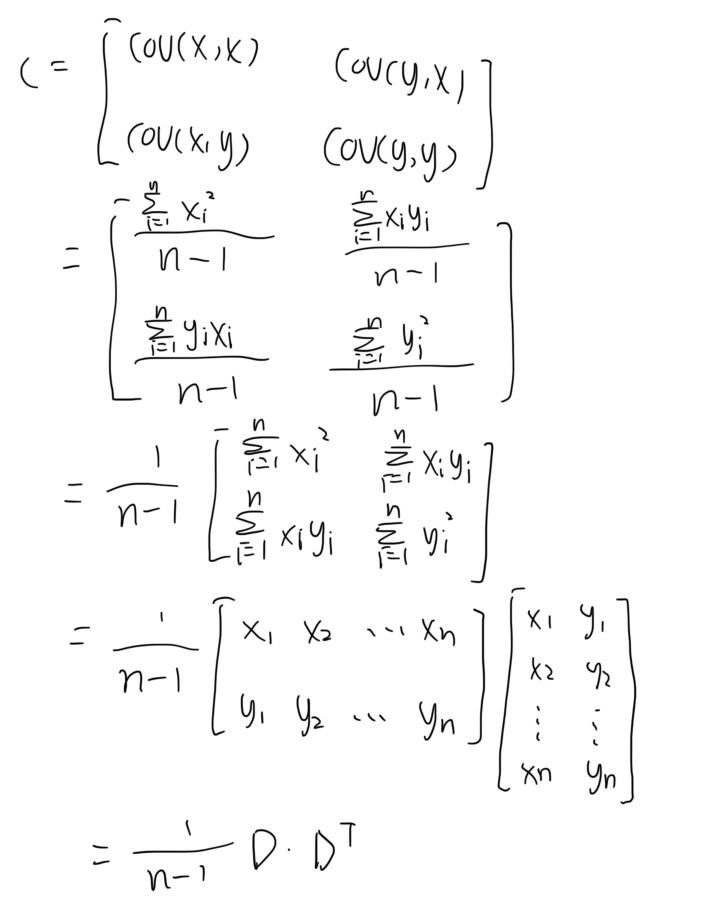
从这个公式可以看出,协方差矩阵的计算依赖于原数据构成的矩阵,这里为了方便我们统一以二维举例,那么最后的x1 x2 y1 y2表示的就是二维坐标下的点,我们将其记录为数据矩阵D。而在前面我们得到了原始数据和处理结果之间基于旋转R和拉伸S的转换关系,那么带入后可以继续往后写。
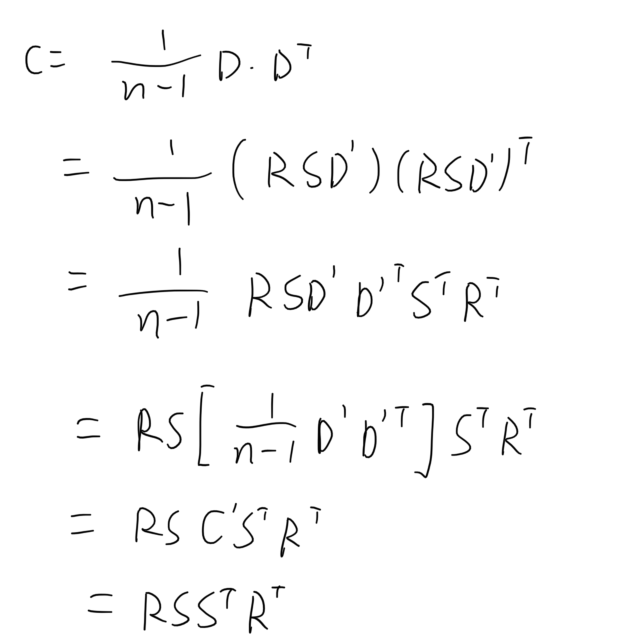
在这个过程中主要有这么几步需要解释一下,首先右上角加’表示的是最终结果,这个与前面的推导稍微有点不同但是一个意思。在第四行,括号内对应的刚好是目标坐标系的协方差矩阵,因此括号的内容在第五行合成为了C’,由于前面我们假定了目标坐标系的数据在两个方向都符合高斯分布,所以协方差矩阵为单位矩阵,所以在第六行可以直接消去C’,从而得到最后的计算结果。由于S本身是一个对角阵,因此转置与否都不发生变化,而且R本身是一个正交矩阵,R的转置与逆矩阵相等,所以我们进行如下的操作。
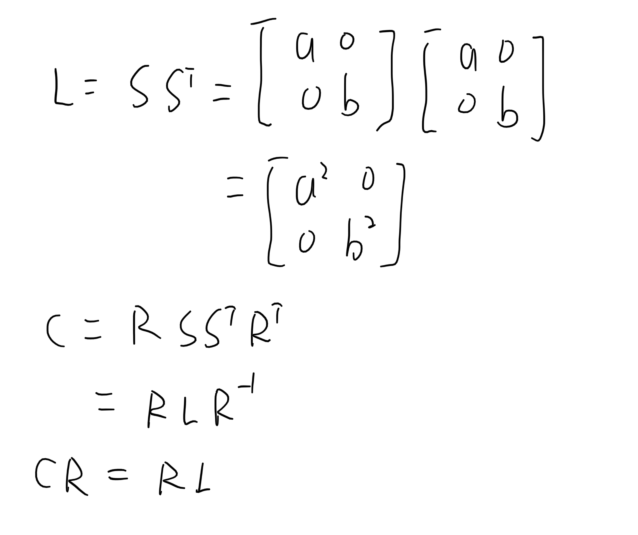
从最终结果来看,这个结果其实对应了考研数学中老生常谈的矩阵对角化,C表示的是原始数据的协方差矩阵,L本身为对角阵,因此就是由特征值组成的对角矩阵,R则为特征向量拼成的矩阵。所以我们要求R和S,就需要先计算原始数据的协方差矩阵,对这个矩阵做对角化,结果的特征向量组成的矩阵就是旋转R,特征值对角阵开方得到的就是拉伸S。
SVD奇异值分解
SVD本身和矩阵对角化是相通的,矩阵对角化要求矩阵必须是一个方阵,这个时候可以计算出特征值和特征向量,而当矩阵本身不是方阵时,我们就无法计算特征值与特征向量,与之相对应的就变成奇异值,当矩阵为方阵的时候,奇异值和特征值就是一个东西。类似于对角化,奇异值分解本身也是要寻找矩阵,由于不是方阵,这里目标变成了三个矩阵。
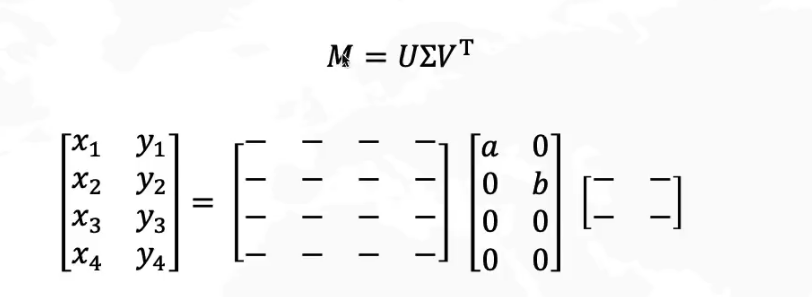
奇异值分解的过程本身也可以用拉伸旋转的理论来解释,我们将M看作是一个线性变换,我们希望找到一个基,这个基在线性变换前后依然可以保持正交,这个就是SVD的主要任务。假设V是原始域的标准正交基,U是经过M变换后的标准正交基,由于SVD本身要求变换前后保持正交即可,所以结果的U不一定是标准正交基,这里额外补充一个伸缩б1和б2用于实现这个正交的对齐。那么我们可以写出下面的等式:
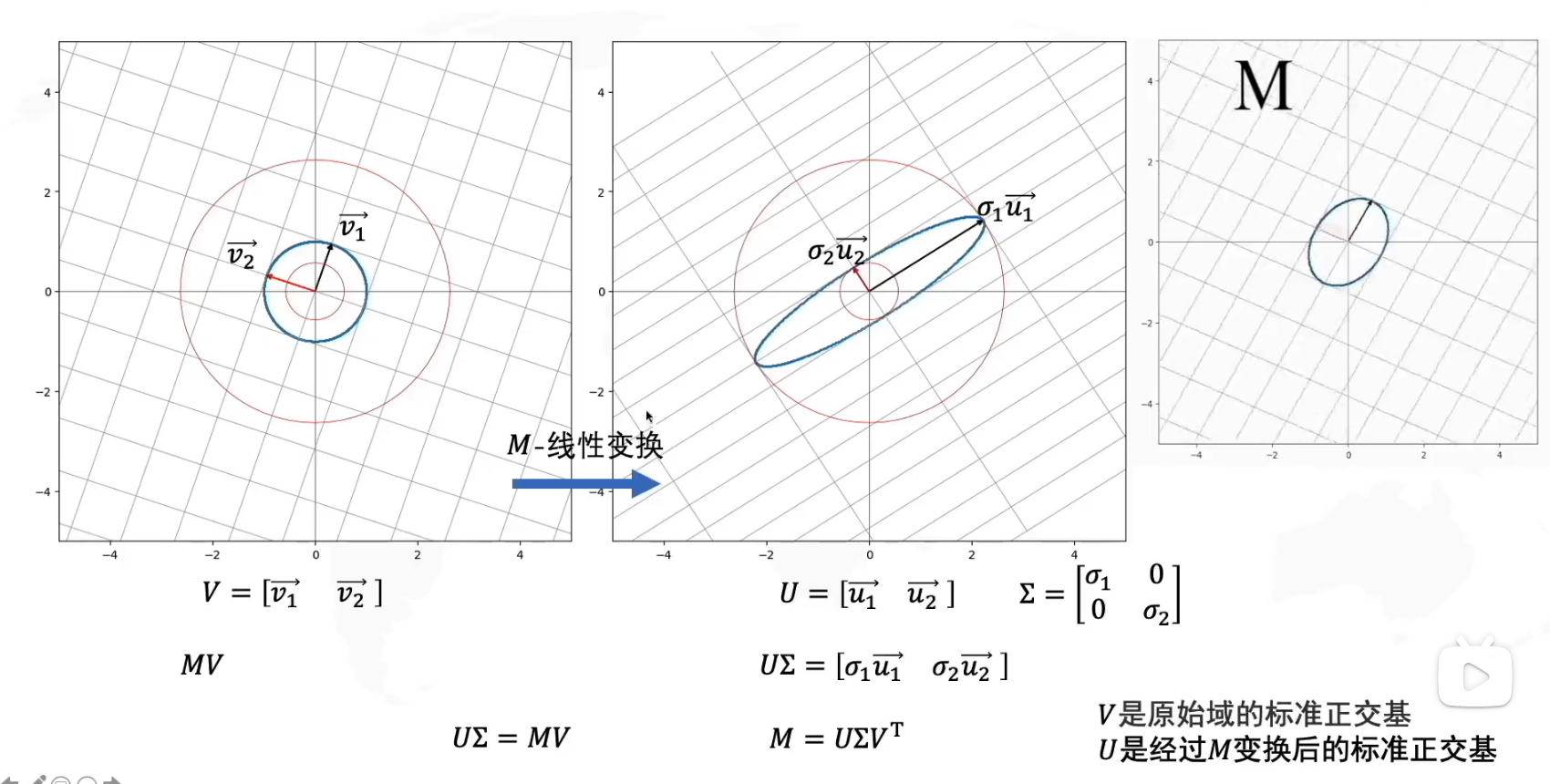
得到了M的表示,那么我们可以继续进行后续的推理:

在这部分公式中,左侧第三行到第四行中,由于U本身表示的是标准正交基组成的矩阵,其转置右乘原矩阵等于单位矩阵,因此在这一步中进行了消去,第四行中的操作和前面PCA的过程基本相似,∑本身不一定是方阵,但其依然符合主对角线上有元素其余位置均为零,所以依然可以整合为一个平方的矩阵,这里就是记作了L,也就是到了第五行的位置,在第五行中,L已经变成了一个方阵,公式左侧也是一个方阵,这时等式的形式就转变为了矩阵对角化的结果,左侧是原矩阵,右侧的L为特征值组成的对角矩阵,V表示特征向量组成的矩阵,所以对MTM和MMT分别进行对角化,就可以计算出线性变化前后的两个基底,对特征值矩阵进行开方,就可以得到伸缩系数。

PCA与SVD的关系
在PCA中我们需要的旋转R和SVD中的V是一样的,也就是说SVD的V就是PCA的主成分的方向。
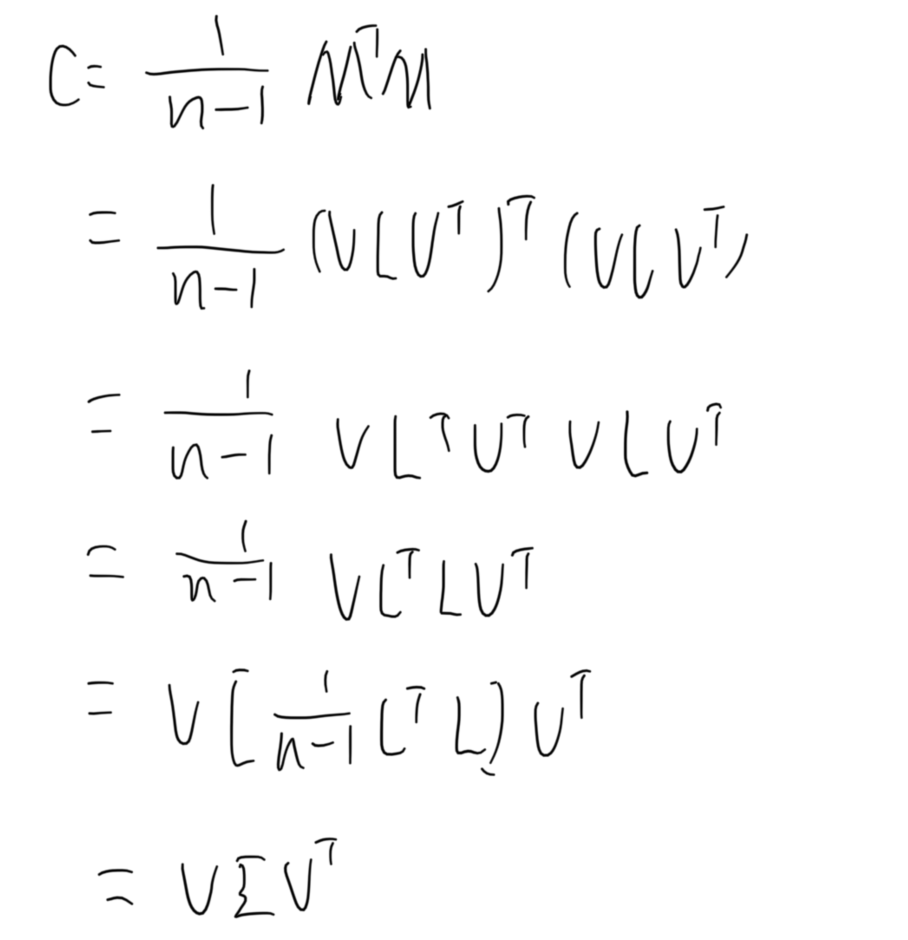
这二者之间的关系主要通过这个V矩阵进行联系,PCA需要先计算协方差矩阵,计算量可能会比较大,反过来用SVD的话,可以不计算协方差矩阵直接求出V。
相关文章:
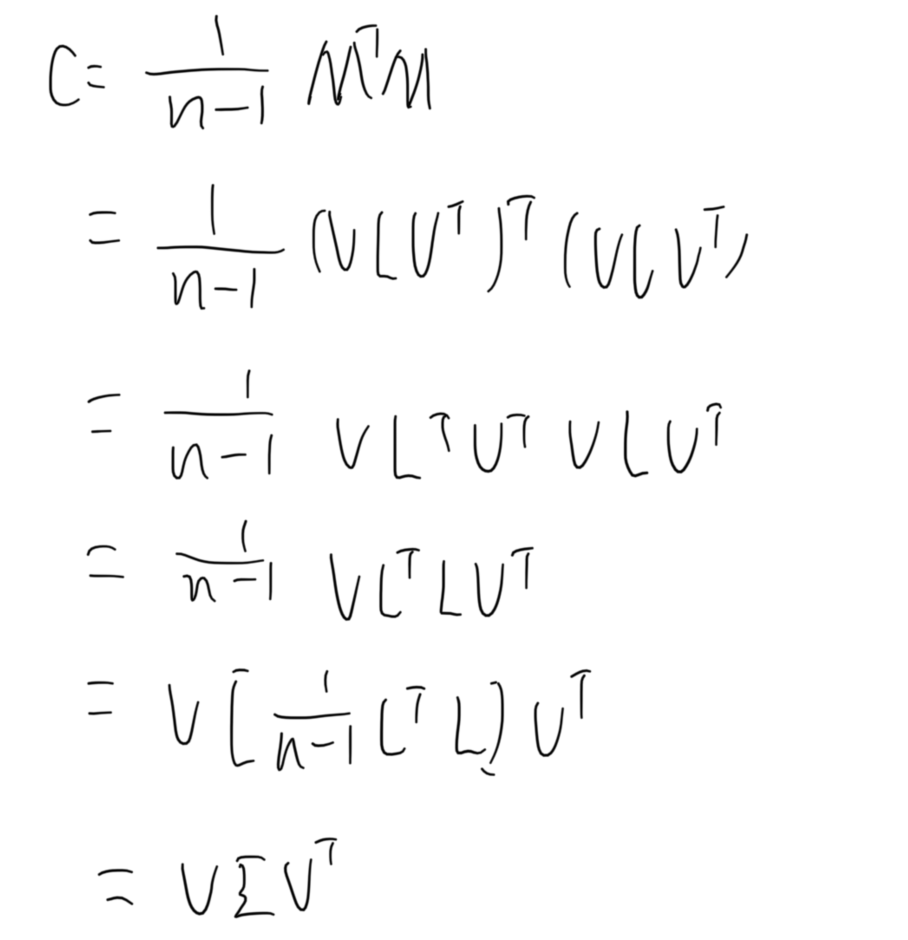
【学习记录】PCA主成分分析 SVD奇异值分解
在看MSC-VO代码的过程中,大量出现了奇异值分解的内容,本身对这部分了解不多,这里补一下课,参考b站up主小旭学长的视频,链接为:PCA主成分分析和SVD主成分分析 PCA主成分分析 PCA根本目的在于让数据在损失尽…...
用 Python 调用 GPT-3 API
用 Python 调用 GPT-3 API GPT-3 是去年由 Open AI 推出的语言机器学习模型。它因其能够写作、写歌、写诗,甚至写代码而获得了广泛的媒体关注!该工具免费使用,只需要注册一个电子邮件即可。 GPT-3 是一种叫 transformer 的机器学习模型。具体…...

类和对象实操之【日期类】
✨个人主页: Yohifo 🎉所属专栏: C修行之路 🎊每篇一句: 图片来源 The pessimist complains about the wind; the optimist expects it to change; the realist adjusts the sails. 悲观主义者抱怨风;乐观主义者期望它…...
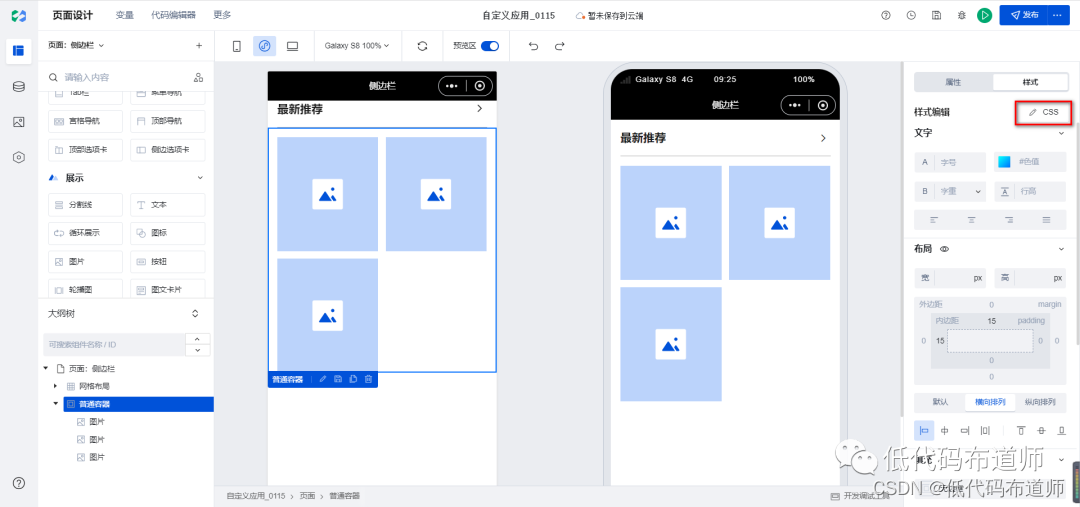
微搭中如何实现弹性布局
我们在实际开发中经常可能会有一些社交的场景,比如开发一个类似朋友圈九宫格图片展示的功能。因为图片的数量不确定,所以需要实现图片的从左到右顺序排列。 在微搭中可以以可视化的方式设置样式。但是对于我们这类特殊需求,只用可视化设置显…...

九龙证券|外资强势出手!这只科创板百元股,被疯狂加仓
本周,北上资金净买入29.32亿元,连续第13周加仓A股。分商场看,北上资金加仓重点倾向于沪市的白马蓝筹股,沪股通取得50.34亿元,深股通则被净卖出21.02亿元。 食品饮料本周取得逾23亿元的增持,居职业首位&…...
)
51单片机最强模块化封装(4)
文章目录 前言一、创建key文件,添加key文件路径二、key文件编写三、模块化测试总结前言 本篇文章将为大家带来按键的模块化封装,这里使用到了三行按键使得我们的代码更加简便。 按键原理:独立按键 一、创建key文件,添加key文件路径 这里的操作就不过多解释了,大家自行看…...
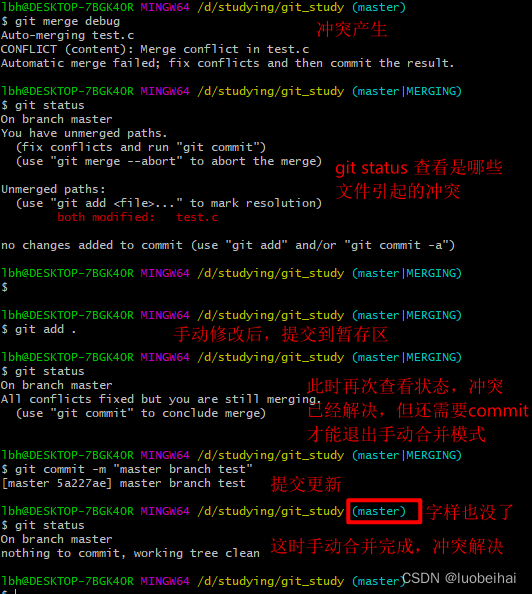
五、Git本地仓库基本操作——分支管理
1. 什么是分支? master分支 我们在初始化git仓库的时候,会默认创建一个master分支,HEAD指针这时就会默认执行master分支。当我们在master分支提交(commit)了更新之后,master分支就会指向当前当前最新的co…...

vscode搭建python Django网站开发环境
这里使用pip安装的方式,打开命令行,输入执行: pip install django2.2这里选择安装2.2版本是因为是新的lts版本,长期支持稳定版。 接下来再安装pillow,Django底层一部分是基于pillow进行的。 pip install pillowpylint…...
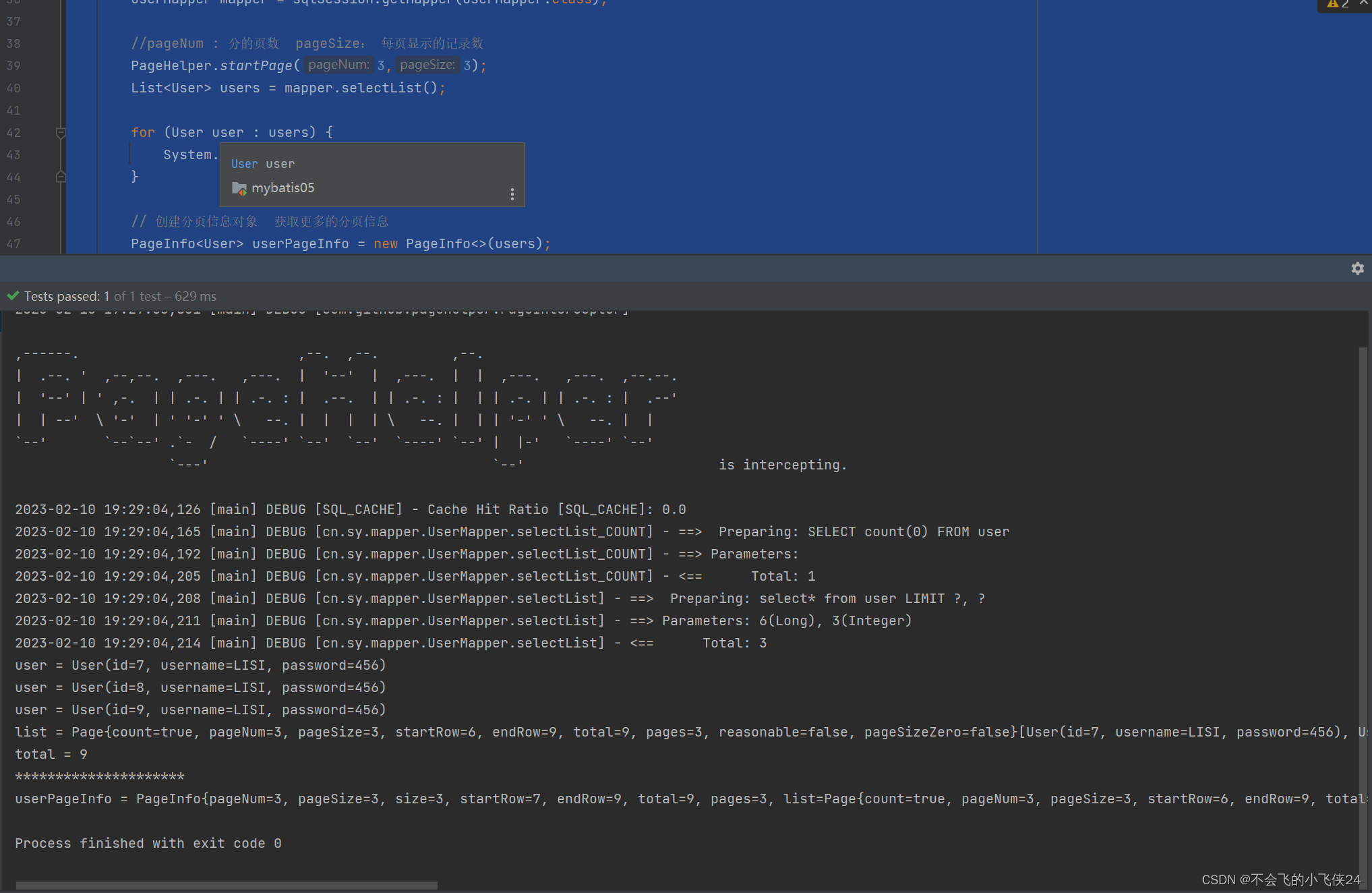
【mybatis】实现分页查询
一 .使用原生分页器的实体类 1.1 java代码部分 方法多 不易书写 package cn.bdqn.entity;public class Page {private Integer pageIndex;//页码private Integer pageSize;//页大小 显示多少行数据private Integer totalCounts;//数据的总行数private Integer totalPages;//…...

CF1560D Make a Power of Two 题解
CF1560D Make a Power of Two 题解题目链接字面描述题面翻译题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示思路代码实现备注题目 链接 https://www.luogu.com.cn/problem/CF1560D 字面描述 题面翻译 给定一个整数 nnn。每次操作你可以做两件事情中的一件&am…...

C#开发的OpenRA的读取文件的函数
C#开发的OpenRA的读取文件的函数 在OpenRA游戏里,读取文件是必备的功能。 因为游戏大部分文件都是图片、动画、语音。 很久以前,我以为开发游戏的主要功能是在程序开发上, 其实游戏的大部分工作都不是在开发上,而是在美工方面。 因为游戏跟电影是一样,就是不断地展示场景,…...

SpringBoot结合XXL-JOB实现定时任务
Quartz的不足 Quartz 的不足:Quartz 作为开源任务调度中的佼佼者,是任务调度的首选。但是在集群环境中,Quartz采用API的方式对任务进行管理,这样存在以下问题: 通过调用API的方式操作任务,不人性化。需要…...

【Node.js】 创建web服务器
Node.js什么是客户端,什么是服务器服务器和普通电脑的区别什么是http模块导入http模块服务器相关概念创建web服务器的基本步骤req请求对象req响应对象解决中文乱码根据不同的url响应不同的html内容什么是客户端,什么是服务器 客户端在网络节点中&#x…...

基于go语言实现RestFul交互
一、RestFul 1.1 RestFul的介绍 RESTFUL(Representational State Transfer)是一种网络应用程序的设计风格和开发方式,基于HTTP或HTTPS,可以使用XML格式定义或JSON格式定义。RESTFUL适用于移动互联网厂商作为业务接口的场景&…...

情感溢出:读《浣溪沙》
浣溪沙 谁念西风独自凉 作者 纳兰性德 谁念西风独自凉,萧萧黄叶闭疏窗,沉思往事立残阳。 被酒莫惊春睡重,赌书消得泼茶香,当时只道是寻常。 记得年轻时学这篇词,就是愣背,现在也就记得这句当时只道是寻常…...
深入解读.NET MAUI音乐播放器项目(一):概述与架构
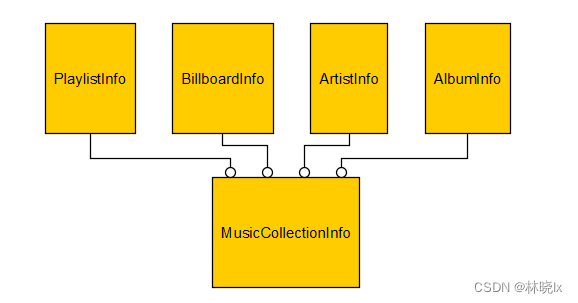
系列文章将分步解读音乐播放器核心业务及代码: 深入解读.NET MAUI音乐播放器项目(一):概述与架构深入解读.NET MAUI音乐播放器项目(二):播放内核深入解读.NET MAUI音乐播放器项目(三…...

【Python小游戏】某程序员将套圈游戏玩儿到了巅峰,好嗨哟~Pygame代码版《牛牛套圈》已上线,大人的套圈游戏太嗨了,小孩勿进。
前言 世上选择那么多。 关注栗子同学会是您最明智的选择哦。 所有文章完整的素材源码都在👇👇 粉丝白嫖源码福利,请移步至CSDN社区或文末公众hao即可免费。 “幸运牛牛套圈圈”套住欢乐,圈住幸福,等你来挑战…...

php的declare命令如何使用?
php中的declare结构用来设定一段代码的执行指令declare用于执行3个指令:ticks,encoding,strict_typesdeclare结构用于全局范围,影响到其后的所有代码(但如果有declare结构的文件被其他文件包含,则对包含他的父文件不起作用&#x…...
嵌软工程师要掌握的硬件知识2:一文看懂什么开漏和推挽电路(open-drain / push-pull)
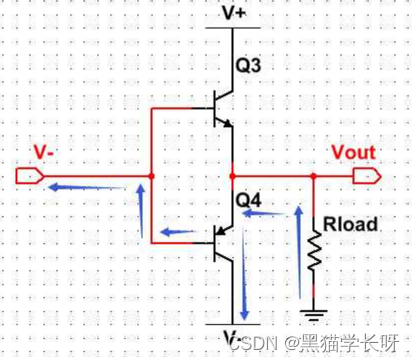
想了解开漏和推挽,就要先了解一下三极管和场效应管是什么,在其他章节有详细介绍,本文就不再进行赘述。 1 推挽(push pull)电路 1.1 理解什么是推挽电路 - 详细介绍 如图所示,Q3是个NPN型三极管,Q4是个PNP型三极管。 1)当Vin电压为正时,上面的N型三极管控制端有电…...

1.2.6存储结构-磁盘管理:单缓冲区与双缓冲区读取、流水线周期、计算流水线执行时间
1.2.6存储结构-磁盘管理:单缓冲区与双缓冲区读取、流水线周期、计算流水线执行时间流水线周期计算流水线执行时间微秒,时间单位,符号μs(英语:microsecond ),1微秒等于百万分之一秒(…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...
