1.2.6存储结构-磁盘管理:单缓冲区与双缓冲区读取、流水线周期、计算流水线执行时间
1.2.6存储结构-磁盘管理:单缓冲区与双缓冲区读取、流水线周期、计算流水线执行时间
- 流水线周期
- 计算流水线执行时间
微秒,时间单位,符号μs(英语:microsecond ),1微秒等于百万分之一秒(10的负6次方秒),1毫秒等于千分之一秒(10的负3次方秒)。
假设磁盘块与缓冲区大小相同,每个盘块读入缓冲区的时间为15μs(微秒),由缓冲区送至用户区的时间是5μs,在用户区内系统对每块数据处理时间为11μs,若用户需要将大小为10个磁盘块的Doc1文件逐块从磁盘读入缓冲区,并送至用户区进行处理,那么采用单缓冲区需要花费的时间为(201)μs;采用双缓冲区需要花费的时间为(156)μs。
这道题中处理数据有三个步骤:
- 从磁盘读入到缓冲区(15μs)
- 从缓冲区读入到(内存)用户区(5μs)
- 处理(内存)用户区数据(1μs)
单缓冲区:
步骤1和2都需要访问临界资源——缓冲区,所以需要合并成一个操作阶段。
使用缓冲区时不能并行,必须分开执行,时间为15μs+5μs20μs;其次处理数据1μs。
构造成流水线后,整个过程划分为2个阶段,1. 从磁盘读入到缓冲区(15μs),同时从缓冲区读入到用户区(5μs),共20μs,2. 处理(内存)用户去数据(1μs)。 根据流水线处理公式,
流水线执行时间=20μs+1μs+(10-1)×20μs=201μs
双缓冲区:
可以实现读入到缓冲区2和从缓冲区1读入到用户区的并发。
读入缓冲区,和从缓冲区读入用户区,可以对不同的缓冲区进行,也就是说,步骤1和2可以并行处理。
对于这里构造成流水线后,整个过程划分为3个阶段: 1. 从磁盘读入到缓冲区(15μs),2. 从缓冲区读入到用户区(5μs),3. 处理(内存)用户去数据(1μs)。 根据流水线执行公式,
流水线执行时间=15μs+5μs+1μs+(10-1)×15μs=156μs
图解如下

流水线周期
流水线应用过程中,会将需要处理的工作分为N个阶段,最耗时的那一段所消耗的时间称为流水线周期。
如:使用流水线技术执行100条指令,每条指令取指2ms,分析4ms,执行1ms,则流水线周期为4ms。
计算流水线执行时间
延续上面场景,将1个任务的执行过程可分成N个阶段,假设每个阶段完成时间为t,则完成该任务所需的时间为Nt。若以传统的方式,则完成k个任务的时间为kNt;而使用流水线技术执行,且花费的时间是Nt+(k-1)t。也就是说。除了第一个任务需要完整的时间外,其他都通过并行,节省了大量的时间。所以流水线的执行时间可通俗的表达为:
流水线执行时间=第1条指令的执行时间+(n−)×流水线周期流水线执行时间=第1条指令的执行时间+(n-)×流水线周期 流水线执行时间=第1条指令的执行时间+(n−)×流水线周期
注意:n表示需要处理的任务数量
考试时,又需要注意一个细节,流水线的执行时间计算,进一步可以分为理论情况与实际情况两种不同的方式。
比如:
某计算机系统,一条指令的执行时间需要经历取指(2ms),分析(4ms),执行(1ms)三个阶段,现要执行100条指令,利用流水线技术需要多长时间?
理论上来说,1条指令的执行时间为:2ms+4ms+1ms=7ms
所以:理论流水线执行时间=2ms+4ms+1ms+(100-1)×4ms=403ms
而实际上,真正做流水线处理时,考虑到处理的复杂性,会将指令的每个执行阶段的时间都统一为流水线周期,即1条指令的执行时间为:4ms+4ms+4ms=12ms
所以:实际流水线执行时间=4ms+4ms+4ms+(100-1)×4ms=408ms
考试时80%以上的概率采用理论公式计算,如果理论公式计算结果无正确选项,再用实际公式计算。
相关文章:

1.2.6存储结构-磁盘管理:单缓冲区与双缓冲区读取、流水线周期、计算流水线执行时间
1.2.6存储结构-磁盘管理:单缓冲区与双缓冲区读取、流水线周期、计算流水线执行时间流水线周期计算流水线执行时间微秒,时间单位,符号μs(英语:microsecond ),1微秒等于百万分之一秒(…...

【pytest接口自动化测试】结合单元测试框架pytest+数据驱动模型+allure
api: 存储测试接口 conftest.py :设置前置操作 目前前置操作:1、获取token并传入headers,2、获取命令行参数给到环境变量,指定运行环境commmon:存储封装的公共方法 connect_mysql.py:连接数据库http_requests.py: 封装…...

展锐平台WIFI吞吐问题解决方案
同学,别退出呀,我可是全网最牛逼的 WIFI/BT/GPS/NFC分析博主,我写了上百篇文章,请点击下面了解本专栏,进入本博主主页看看再走呗,一定不会让你后悔的,记得一定要去看主页置顶文章哦。 一、Wi-Fi 吞吐验收标准 预置条件:屏蔽房;DUT 距离 AP 1m 左右;测试 AP 不加密;…...

全局向量的词嵌入(GloVe)
诸如词-词共现计数的全局语料库统计可以来解释跳元模型。 交叉熵损失可能不是衡量两种概率分布差异的好选择,特别是对于大型语料库。GloVe使用平方损失来拟合预先计算的全局语料库统计数据。 对于GloVe中的任意词,中心词向量和上下文词向量在数学上是等…...
,真题含思路)
华为OD机试 - 特异性双端队列(Python),真题含思路
特异性双端队列 题目 有一个特异性的双端队列,该队列可以从头部到尾部添加数据,但是只能从头部移除数据。 小 A 一次执行 2 n 2n 2n 个指令往队列中添加数据和移除数据, 其中 n n n 个指令是添加数据(可能从头部也可以从尾部添加) 依次添加 1 到...
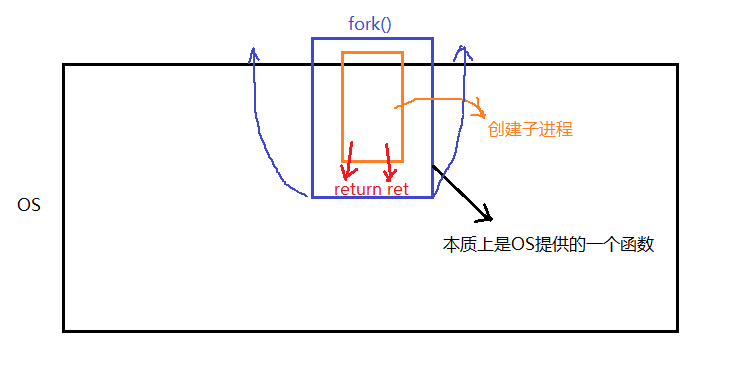
【Linux】操作系统进程概念
文章目录1. 冯诺依曼体系结构2. 操作系统3. 进程进程的基本概念查看进程和杀死进程父进程和子进程通过系统调用创建子进程1. 冯诺依曼体系结构 冯诺依曼结构也称普林斯顿结构,是一种将程序指令存储器和数据存储器合并在一起的存储器结构。数学家冯诺依曼提出了计算…...

C语言const的用法详解
有时候我们希望定义这样一种变量,它的值不能被改变,在整个作用域中都保持固定。例如,用一个变量来表示班级的最大人数,或者表示缓冲区的大小。为了满足这一要求,可以使用const关键字对变量加以限定:constin…...
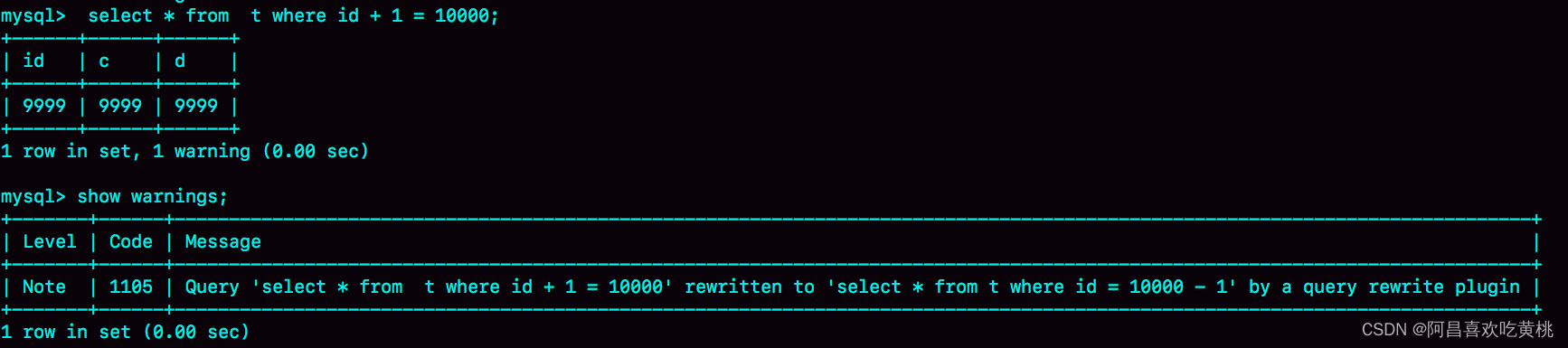
Day886.MySQL的“饮鸩止渴”提高性能的方法 -MySQL实战
MySQL的“饮鸩止渴”提高性能的方法 HI,我是阿昌,今天学习记录的是关于MySQL的“饮鸩止渴”提高性能的方法的内容。 不知道在实际运维过程中有没有碰到这样的情景: 业务高峰期,生产环境的 MySQL 压力太大,没法正常响…...
08- 数据升维 (PolynomialFeatures) (机器学习)
在做数据升维的时候,最常见的手段就是将已知维度进行相乘(或者自乘)来构建新的维度 使用 np.concatenate()进行简单的,幂次合并,注意数据合并的方向axis 1 数据可视化时,注意切片,因为数据升维…...
)
2023备战金三银四,Python自动化软件测试面试宝典合集(二)
马上就又到了程序员们躁动不安,蠢蠢欲动的季节~这不,金三银四已然到了家门口,元宵节一过后台就有不少人问我:现在外边大厂面试都问啥想去大厂又怕面试挂面试应该怎么准备测试开发前景如何面试,一个程序员成长之路永恒绕…...

笔试题-2023-紫光展锐-数字芯片设计【纯净题目版】
回到首页:2023 数字IC设计秋招复盘——数十家公司笔试题、面试实录 推荐内容:数字IC设计学习比较实用的资料推荐 题目背景 笔试时间:2022.08.24应聘岗位:数字芯片设计工程师笔试时长:90min笔试平台:nowcoder牛客网题目类型:单选题(18道)、不定项选择题(22道)题目评…...
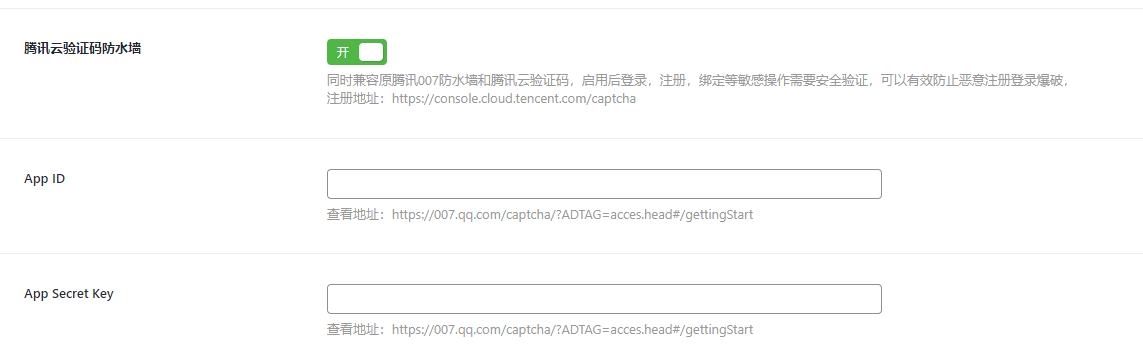
WordPress网站日主题Ri主题RiProV2主题开启了验证码登录但是验证码配置不对结果退出登录后进不去管理端了
背景 WordPress网站日主题Ri主题RiProV2主题开启了验证码登录但是验证码配置不对结果退出登录后进不去管理端了;开启了腾讯云验证码防火墙但APPID,APPSecret没配置,结果在退出登录后,由于验证码验证失败管理端进不去了 提示如下:...

自动驾驶感知——毫米波雷达
文章目录1. 雷达的基本概念1.1 毫米波雷达分类1.2 信息的传输1.3 毫米波雷达的信号频段1.4 毫米波雷达工作原理1.4.1 毫米波雷达测速测距的数学原理1.4.2 毫米波雷达测角度的数学原理1.4.3 硬件接口1.4.4 关键零部件1.4.5 数据的协议与格式1.5 车载毫米波雷达的重要参数1.6 车载…...
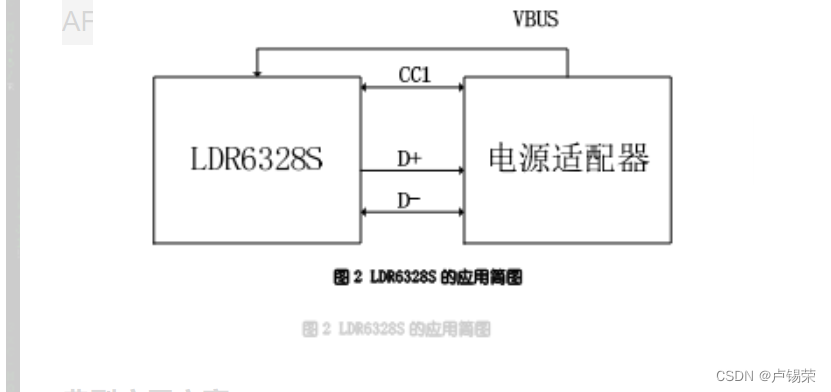
取电芯片全协议都可兼容
乐得瑞PD协议芯片/PD取电芯片/PD受电端协议芯片 支持5/9/12/15/20v定制 1、概述 LDR6328S 是乐得瑞科技有限公司开发的一款兼容 USB PD、QC 和 AFC 协议的 Sink 控制器。 LDR6328S 从支持 USB PD、QC 和 AFC 协议的适配器取电,然后供电给设备。比如可以配置适配器输…...

自己总结优化代码写法
jdk1.7新特性详解 开发期间略知jdk1.7的一些特性,没有真正的一个一个得展开研究,而是需要说明再去查,导致最整个新特性不是特别的清楚,这种情况以后得需要改变了,否则就会变成代码的奴隶。现在正好有时间可以细细的研…...

Java体系最强干货分享—挑战40天准备Java面试,最快拿到offer!
如何准备java面试,顺利上岸大厂java岗位? 主攻Java的人越来越多,导致行业越来越卷,最开始敲个“hello world”都能进大厂,现在,八股、全家桶、算法等等面试题横行,卷到极致!就拿今年…...

云计算|OpenStack|错误记录和解决方案(不定时更新)
前言: openstack的部署和使用是难度比较大的,难免会出现各种各样的问题,因此,本文将把一些在部署和使用openstack社区版时出现的错误做一个记录,并就每一个错误分析和解决问题。(尽量记录比较经典的错误&a…...
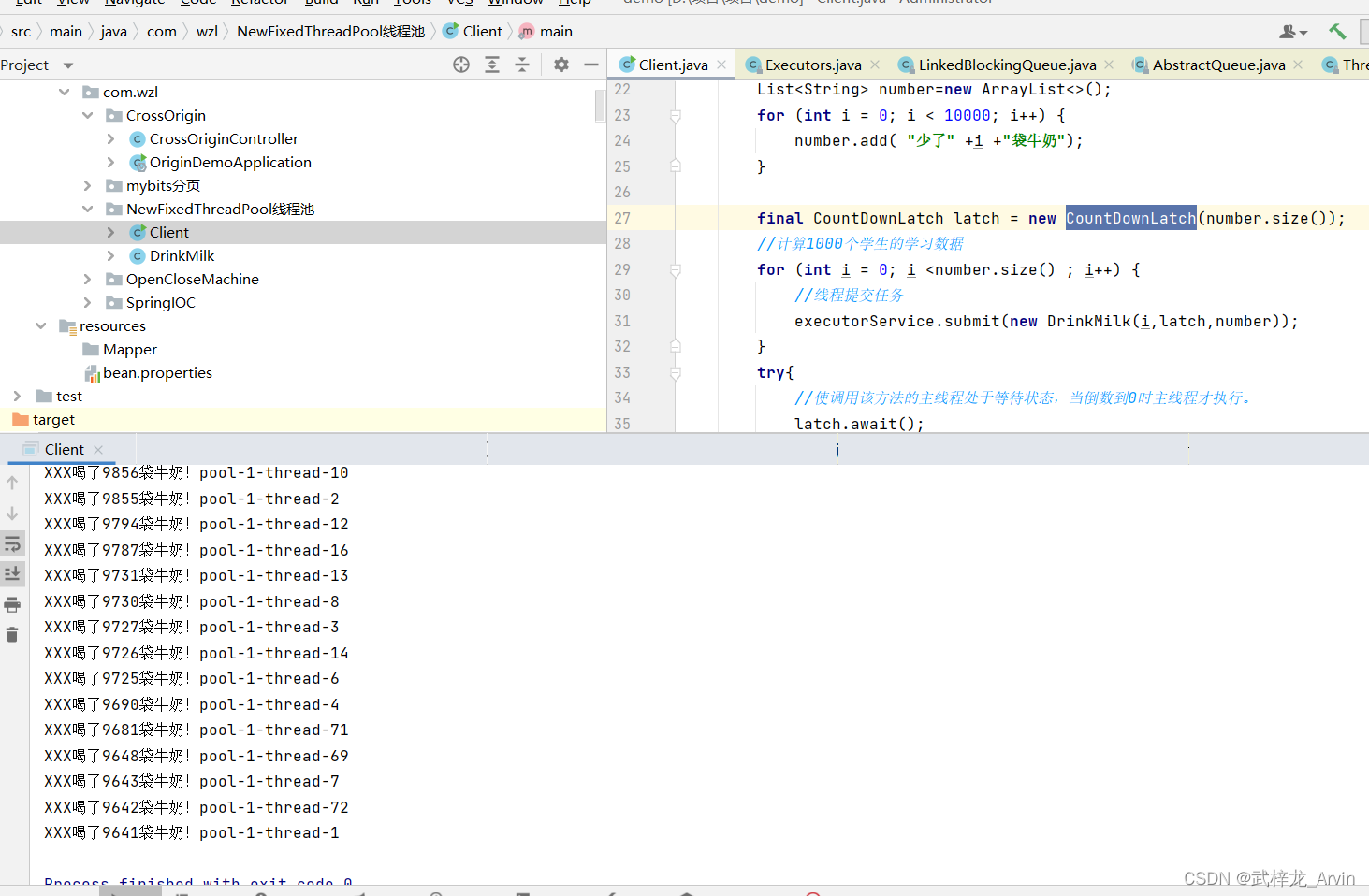
项目实战-NewFixedThreadPool线程池
目录 什么是线程池 线程池的类型 1.CachedThreadPool 2.FixedThreadPool 3.ScheduledThreadPool 4.SingleThreadPool 5.newWorkStealingPool 线程池的好处 1、线程池的重用 2、控制线程池的并发数 3、线程池可以对线程进行管理 线程池的示例 1.Client启动类 2.具体…...

导数与微分总复习——“高等数学”
各位CSDN的uu们你们好呀,今天,小雅兰来复习一下之前学过的知识点,也就是导数与微分的总复习,依旧是高等数学的内容,主要是明天就要考高等数学了,哈哈哈,下面,让我们一起进入高等数学…...

Linux软件安装
1.Linux安装JDK 1.安装位置 /opt 2.安装包 jdk-8u171-linux-x64.rpm 3.安装步骤 1.将安装包上传到虚拟机中 [rootlocalhost opt]# ls jdk-8u171-linux-x64.rpm2.执行安装命令 [rootlocalhost opt]# rpm -ivh jdk-8u171-linux-x64.rpm 准备中... #####…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
