08- 数据升维 (PolynomialFeatures) (机器学习)
- 在做数据升维的时候,最常见的手段就是将已知维度进行相乘(或者自乘)来构建新的维度
-
使用 np.concatenate()进行简单的,幂次合并,注意数据合并的方向axis = 1
-
数据可视化时,注意切片,因为数据升维后,多了平方这一维
-
# 4、多项式升维 + 普通线性回归
X = np.concatenate([X,X**2],axis = 1)- 使用 PolynomialFeatures 进行 特征升维
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures() # 使用PolynomialFeatures进行特征升维
poly.fit(X,y)
X = poly.transform(X)- 调整字体大小: plt.rcParams[ 'font.size' ] = 18
import matplotlib.pyplot as plt
plt.rcParams['font.size'] = 181.1、多项式回归基本概念
对于多项式回归来说主要是为了扩展线性回归算法来适应更广泛的数据集,比如我们数据集有两个维度 ,那么用多元线性回归公式就是:
,当我们使用二阶多项式升维的时候,数据集就从原来的
扩展成了
。因此多元线性回归就得去多计算三个维度所对应的w值:
。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression# 1、创建数据,并进行可视化
X = np.linspace(-1,11,num = 100)
y = (X - 5)**2 + 3*X -12 + np.random.randn(100)
X = X.reshape(-1,1)
plt.scatter(X,y)# 2、创建预测数据
X_test = np.linspace(-2,12,num = 200).reshape(-1,1)# 3、不进行升维 + 普通线性回归
model_1 = LinearRegression()
model_1.fit(X,y)
y_test_1 = model_1.predict(X_test)
plt.plot(X_test,y_test_1,color = 'red')# 4、多项式升维 + 普通线性回归
X = np.concatenate([X,X**2],axis = 1)
model_2 = LinearRegression()
model_2.fit(X,y)
# 5、测试数据处理,并预测
X_test = np.concatenate([X_test,X_test**2],axis = 1)
y_test_2 = model_2.predict(X_test)# 6、数据可视化,切片操作
plt.plot(X_test[:,0],y_test_2,color = 'green')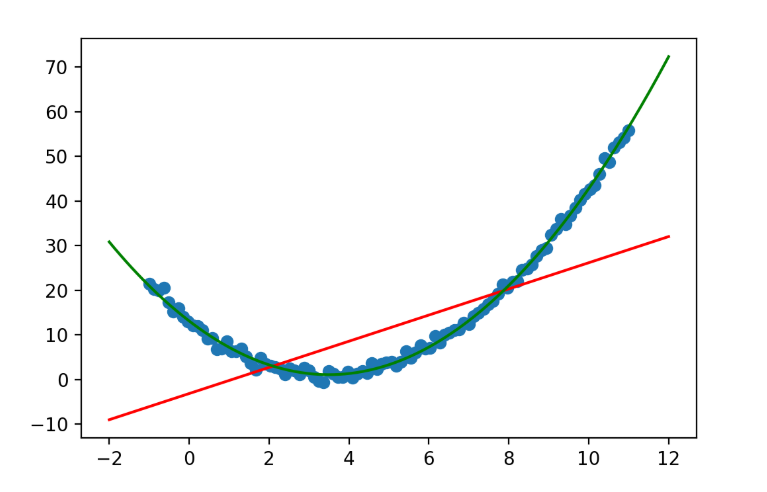
1.2 使用PolynomialFeatures进行特征升维
import matplotlib.pyplot as plt
import numpy as np
from sklearn.preprocessing import PolynomialFeatures,StandardScaler
from sklearn.linear_model import SGDRegressor# 1、创建数据,并进行可视化
X = np.linspace(-1,11,num = 100)
y = (X - 5)**2 + 3*X -12 + np.random.randn(100)
X = X.reshape(-1,1)
plt.scatter(X,y)# 3、使用PolynomialFeatures进行特征升维
poly = PolynomialFeatures() # 特征升维
poly.fit(X,y)
X = poly.transform(X)
s = StandardScaler() # 归一化
X = s.fit_transform(X)# 4、训练模型
model = SGDRegressor(penalty='l2',eta0 = 0.01)
model.fit(X,y)# 2、创建预测数据
X_test = np.linspace(-2,12,num = 200).reshape(-1,1)
X_test = poly.transform(X_test) # 特征升维
X_test_norm = s.transform(X_test) # 归一化
y_test = model.predict(X_test_norm)
plt.plot(X_test[:,1],y_test,color = 'green')1.3 多项式预测
天猫双十一销量与年份的关系是多项式关系!假定,销量和年份之间关系是三次幂关系:
import numpy as np
from sklearn.linear_model import SGDRegressor
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
plt.figure(figsize=(12,9))# 1、创建数据,年份数据2009 ~ 2019
X = np.arange(2009,2020)
y = np.array([0.5,9.36,52,191,350,571,912,1207,1682,2135,2684])# 2、年份数据,均值移除,防止某一个特征列数据天然的数值太大而影响结果
X = X - X.mean()
X = X.reshape(-1,1)# 3、构建多项式特征,3次幂
poly = PolynomialFeatures(degree=3)
X = poly.fit_transform(X)
s = StandardScaler()
X_norm = s.fit_transform(X)# 4、创建模型
model = SGDRegressor(penalty='l2',eta0 = 0.5,max_iter = 5000)
model.fit(X_norm,y)# 5、数据预测
X_test = np.linspace(-5,6,100).reshape(-1,1)
X_test = poly.transform(X_test)
X_test_norm = s.transform(X_test)
y_test = model.predict(X_test_norm)# 6、数据可视化
plt.plot(X_test[:,1],y_test,color = 'green')
plt.bar(X[:,1],y)
plt.bar(6,y_test[-1],color = 'red')
plt.ylim(0,4096)
plt.text(6,y_test[-1] + 100,round(y_test[-1],1),ha = 'center')
_ = plt.xticks(np.arange(-5,7),np.arange(2009,2021))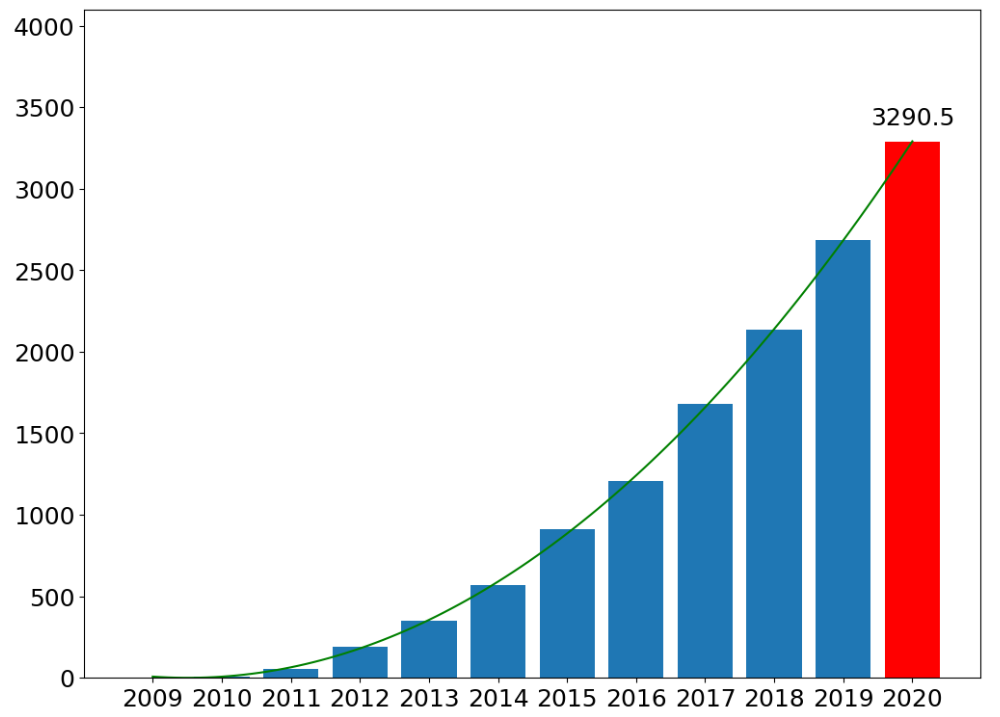
相关文章:

08- 数据升维 (PolynomialFeatures) (机器学习)
在做数据升维的时候,最常见的手段就是将已知维度进行相乘(或者自乘)来构建新的维度 使用 np.concatenate()进行简单的,幂次合并,注意数据合并的方向axis 1 数据可视化时,注意切片,因为数据升维…...
)
2023备战金三银四,Python自动化软件测试面试宝典合集(二)
马上就又到了程序员们躁动不安,蠢蠢欲动的季节~这不,金三银四已然到了家门口,元宵节一过后台就有不少人问我:现在外边大厂面试都问啥想去大厂又怕面试挂面试应该怎么准备测试开发前景如何面试,一个程序员成长之路永恒绕…...

笔试题-2023-紫光展锐-数字芯片设计【纯净题目版】
回到首页:2023 数字IC设计秋招复盘——数十家公司笔试题、面试实录 推荐内容:数字IC设计学习比较实用的资料推荐 题目背景 笔试时间:2022.08.24应聘岗位:数字芯片设计工程师笔试时长:90min笔试平台:nowcoder牛客网题目类型:单选题(18道)、不定项选择题(22道)题目评…...
WordPress网站日主题Ri主题RiProV2主题开启了验证码登录但是验证码配置不对结果退出登录后进不去管理端了
背景 WordPress网站日主题Ri主题RiProV2主题开启了验证码登录但是验证码配置不对结果退出登录后进不去管理端了;开启了腾讯云验证码防火墙但APPID,APPSecret没配置,结果在退出登录后,由于验证码验证失败管理端进不去了 提示如下:...

自动驾驶感知——毫米波雷达
文章目录1. 雷达的基本概念1.1 毫米波雷达分类1.2 信息的传输1.3 毫米波雷达的信号频段1.4 毫米波雷达工作原理1.4.1 毫米波雷达测速测距的数学原理1.4.2 毫米波雷达测角度的数学原理1.4.3 硬件接口1.4.4 关键零部件1.4.5 数据的协议与格式1.5 车载毫米波雷达的重要参数1.6 车载…...
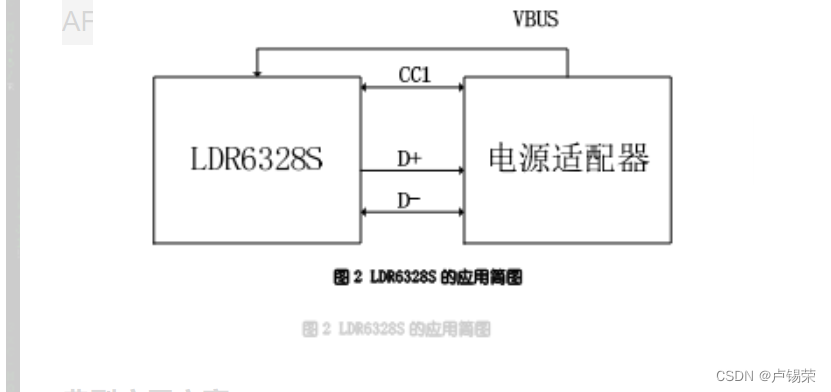
取电芯片全协议都可兼容
乐得瑞PD协议芯片/PD取电芯片/PD受电端协议芯片 支持5/9/12/15/20v定制 1、概述 LDR6328S 是乐得瑞科技有限公司开发的一款兼容 USB PD、QC 和 AFC 协议的 Sink 控制器。 LDR6328S 从支持 USB PD、QC 和 AFC 协议的适配器取电,然后供电给设备。比如可以配置适配器输…...

自己总结优化代码写法
jdk1.7新特性详解 开发期间略知jdk1.7的一些特性,没有真正的一个一个得展开研究,而是需要说明再去查,导致最整个新特性不是特别的清楚,这种情况以后得需要改变了,否则就会变成代码的奴隶。现在正好有时间可以细细的研…...

Java体系最强干货分享—挑战40天准备Java面试,最快拿到offer!
如何准备java面试,顺利上岸大厂java岗位? 主攻Java的人越来越多,导致行业越来越卷,最开始敲个“hello world”都能进大厂,现在,八股、全家桶、算法等等面试题横行,卷到极致!就拿今年…...

云计算|OpenStack|错误记录和解决方案(不定时更新)
前言: openstack的部署和使用是难度比较大的,难免会出现各种各样的问题,因此,本文将把一些在部署和使用openstack社区版时出现的错误做一个记录,并就每一个错误分析和解决问题。(尽量记录比较经典的错误&a…...
项目实战-NewFixedThreadPool线程池
目录 什么是线程池 线程池的类型 1.CachedThreadPool 2.FixedThreadPool 3.ScheduledThreadPool 4.SingleThreadPool 5.newWorkStealingPool 线程池的好处 1、线程池的重用 2、控制线程池的并发数 3、线程池可以对线程进行管理 线程池的示例 1.Client启动类 2.具体…...

导数与微分总复习——“高等数学”
各位CSDN的uu们你们好呀,今天,小雅兰来复习一下之前学过的知识点,也就是导数与微分的总复习,依旧是高等数学的内容,主要是明天就要考高等数学了,哈哈哈,下面,让我们一起进入高等数学…...

Linux软件安装
1.Linux安装JDK 1.安装位置 /opt 2.安装包 jdk-8u171-linux-x64.rpm 3.安装步骤 1.将安装包上传到虚拟机中 [rootlocalhost opt]# ls jdk-8u171-linux-x64.rpm2.执行安装命令 [rootlocalhost opt]# rpm -ivh jdk-8u171-linux-x64.rpm 准备中... #####…...
【表面缺陷检测】基于YOLOX的PCB表面缺陷检测(全网最详细的YOLOX保姆级教程)
写在前面: 首先感谢兄弟们的订阅,让我有创作的动力,在创作过程我会尽最大能力,保证作品的质量,如果有问题,可以私信我,让我们携手共进,共创辉煌。 Hello,大家好,我是augustqi。 今天给大家分享一个表面缺陷检测项目:基于YOLOX的PCB表面缺陷检测(保姆级教程)。多的…...

【C#基础】C# 程序基础语法解析
序号系列文章0【C#基础】初识编程语言C#1【C#基础】C# 程序通用结构总结 文章目录前言基础语法1. using 关键字2. namespace 关键字3. class 关键字4. 成员字段5. 成员方法6. Main 方法7. new 关键字8. 标识符9. 关键字结语前言 😄 大家好,我是writer桑&…...

【webpack】webpack 中的插件安装与使用
一、webpack 插件的作用 通过安装和配置第三方的插件,可以拓展 webpack 的能力,从而让 webpack 用起来更方便。最常用的 的webpack 插件有如下两个: 1.webpack-dev-server(实时打包构建) 类似于 node.js 阶段用到的 no…...
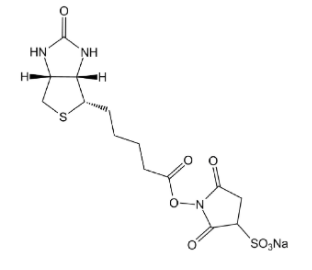
生物素-磺基-活性酯,Sulfo-NHS Biotin科研用试剂简介;CAS:119616-38-5
生物素-磺基-活性酯,Sulfo-NHS Biotin 结构式: 编辑 添加图片注释,不超过 140 字(可选) 英文名称:Sulfo-NHS-Biotin Sulfosuccinimidyl biotin 中文名称:磺酸基-Biotin-N-琥珀酰亚胺基酯 CAS&…...

Debain安装命令
目录 一、安装sudo命令 二、安装jdk8 三、更换软件源 四、Debian 安装 yum 五、安装zip、unzip、curl、lrzsz、NUMA 六、安装Maven 五、问题 一、安装sudo命令 1)执行sudo命令,提示 -bash: sudo: command not found的解决方法 apt-get install s…...
2023-02-10 - 6 聚合
当用户使用搜索引擎完成搜索后,在展示结果中需要进行进一步的筛选,而筛选的维度需要根据当前的搜索结果进行汇总,这就用到了聚合技术。聚合的需求在很多应用程序中都有所体现,例如在京东App中搜索“咸鸭蛋”,然后单击搜…...
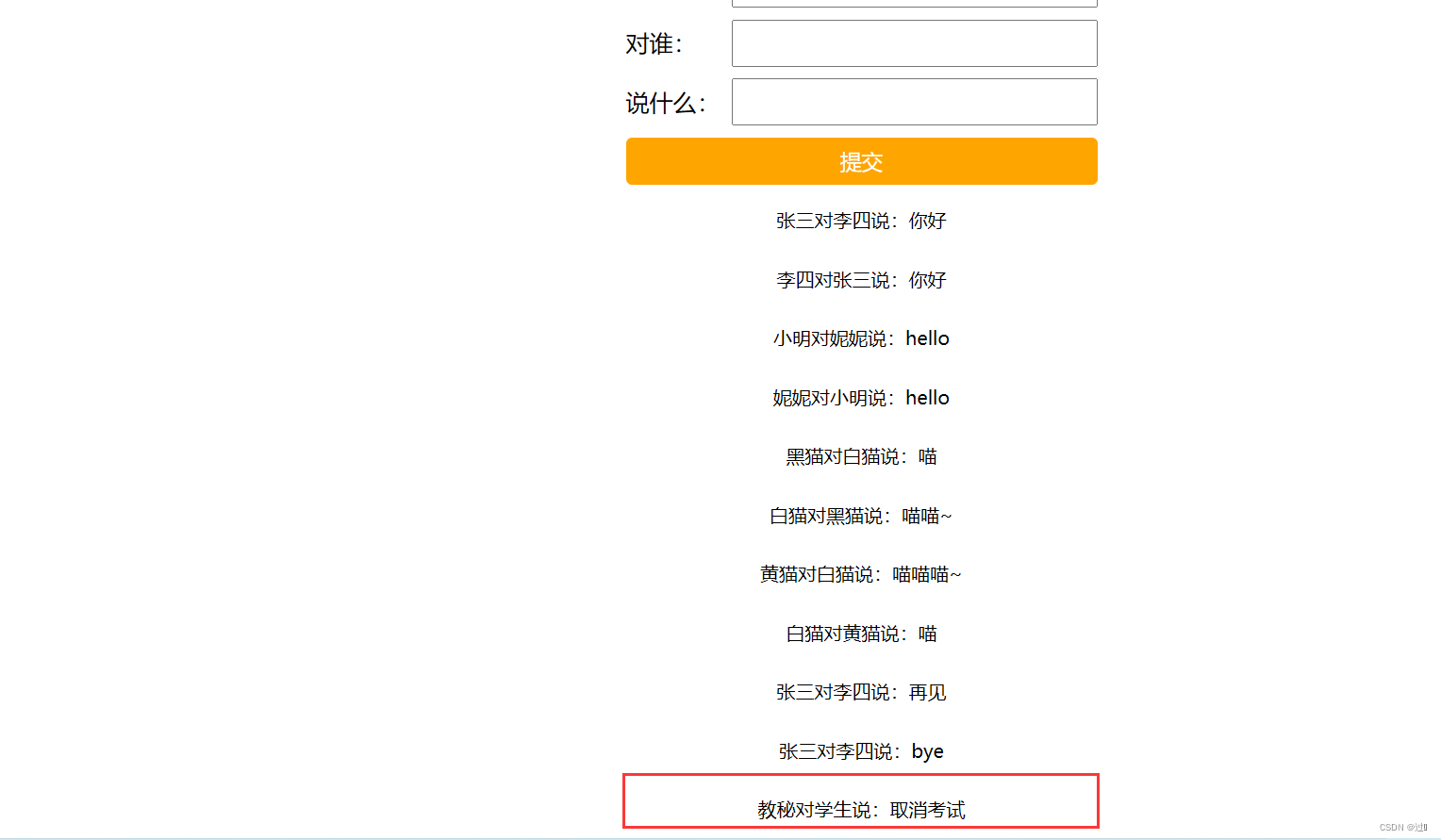
Servlet实现表白墙
目录 一、表白墙简介 二、代码实现 1、约定前后端交互的接口 2、后端代码实现 3、前端代码实现 三、效果演示 一、表白墙简介 在表白墙页面中包含三个文本框,分别表示表白者,表白对象,表白内容,在文本框中输入内容之后&…...

[python入门㊸] - python测试函数
目录 ❤ 测试函数 ❤ 单元测试和测试用例 ❤ 可通过的测试 ❤ 不能通过的测试 ❤ 测试未通过时怎么办 ❤ 添加新测试 ❤ 测试函数 学习测试,得有测试的代码。下面是一个简单的函数: name_function.py def get_formatted_name(first, last):…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

aurora与pcie的数据高速传输
设备:zynq7100; 开发环境:window; vivado版本:2021.1; 引言 之前在前面两章已经介绍了aurora读写DDR,xdma读写ddr实验。这次我们做一个大工程,pc通过pcie传输给fpga,fpga再通过aur…...
