情感溢出:读《浣溪沙》
浣溪沙 谁念西风独自凉
作者 纳兰性德
谁念西风独自凉,萧萧黄叶闭疏窗,沉思往事立残阳。
被酒莫惊春睡重,赌书消得泼茶香,当时只道是寻常。
记得年轻时学这篇词,就是愣背,现在也就记得这句当时只道是寻常。
在听完戴建业老师讲解之后,我不禁潸然泪下,只觉一句“平常就是幸福,一切安好就是幸运”。
一、谁念西风独自凉
在这一句中,作者是回忆自己的亡妻,卢氏(两广总督之女),在过去秋天到来之际,天气转凉,耳畔总会想起,“相公,天凉了,吹坏身子,添上衣裳吧!”,两人相拥,温暖和爱充满心间。而如今,冷热是否,无人问津,还有谁念西风杀气,自个儿吹去。戴老师也想起他的妻子,在过去总是手指一挥,“死老头子,还不去加衣服呀!哇呀呀呀”。这是多么令人羡慕的男女之间的情感,这也是对婚姻充满期待的我的向往之处。冷热有人知,辛苦有人问。
二、萧萧黄叶闭疏窗
秋风吹起黄叶飞,无边落木萧萧下。秋风肃杀,给人一种凄凉之感,蟪蛄不知春秋,秋风萧瑟,作者的心情随着落叶变得低沉,心里千疮百孔,爱妻已逝,吾心谁知。所以,索性闭上这扇窗,不看这苍凉之景,也可偷偷抹泪。
三、沉思往事立残阳
睹物思人,往事朝夕,在这一件件,一处处,无不是爱妻之关心,爱妻之身影。想想新婚之时,喜结连理,夫妻对拜,自此相依。三年间夫妻恩爱,郎才女貌,羡煞旁人。一点一滴浮上心头。不知不觉,太阳快要落山。
四、被酒莫惊春睡重
喝多了酒,昏睡在床上。妻子悄悄咪咪的走过,生怕吵醒我。春天还是有点冷,倒春寒还未过去,喝酒暖身,多了倒头就睡,有个贤惠的妻子,温柔体己,也不怪我酒气满身,依旧贴心服侍。这只是生活中的小细节,想起来还是那么惹人发笑,像一只小猫咪,轻轻柔柔。
五、赌书消得泼茶香
这句话引用了赵明诚、李清照夫妻之间的爱情故事,讲的是李清照和赵明诚之间的夫妻小游戏,李清照记性好,就问丈夫,哪本书哪一行是哪一句,答不上来自己就赢了,可以先喝茶,输了后喝茶,泼的茶到处都是,满屋的茶香。互相嬉戏,爱意满屋。这何尝不是在说作者自己同妻子之间有趣生活,也是爱情的必备。
六、当时只道是寻常
这句话,太过经典,也是本文的结尾,作者想要表达的是对过去生活的怀念,对妻子的思念,也是过去觉得普通平常的思想的批判,也是警示我们,要珍惜平静无波澜的日子,不要等到逝去才觉后悔。珍惜眼前的事物,人,特别是自己的亲人。对爱情要始终保有憧憬,始终向往,哪怕有一天,觉得夫妻之间已找不到趣味,看看这首词,想想当时只道是寻常,如今可望不可及。
和苏东坡的江城子,十年生死两茫茫,不思量,自难忘,千里孤坟,无处话凄凉。纵使相逢应不识,尘满面,鬓如霜。夜来幽梦忽还乡,小轩窗,正梳妆。相顾无言,惟有泪千行。料得年年肠断处,明月夜,短松冈。
纳兰性德从细节入手,将思念化作西风吹人时的问候,化作黄叶萧萧时的闭窗,用立残阳来表达自己的孤寂之感。想起春睡之时的蹑手蹑脚,这些细节,催人泪下。最后化作,当时只道是寻常。
江城子这首词读了一遍就觉得悲痛不已,而这首浣溪沙,却让人久久不能走出来。我的你啊,不如情薄义寡。纳兰性德没有走出来,在妻子逝去七年后离世,只有30岁。而苏东坡生性豁达,很快就走出来了。君本天上多情种,不是人间富贵花。老来多健忘,唯不忘相思。力透纸背意难平。
一辈子,如果没有深沉的去爱过一个人,没有被人深沉的爱过,是人生的一种不幸。如果未来有这么一份爱情等着我去,我会为之付出一生的努力,无论朝夕,无论风雨,勇敢去爱,用心去爱!
希望读到这篇文章的你有着对未来的无限憧憬,这个未来不远,就是明天,今天要好好对待身边的人,对自己的妻子(丈夫)要保持初心,当初的美好是可以一直铭记的,不要等到失去才后悔莫及,这句当时只道是寻常,出现得越少越好,人生无悔,方得始终!
相关文章:

情感溢出:读《浣溪沙》
浣溪沙 谁念西风独自凉 作者 纳兰性德 谁念西风独自凉,萧萧黄叶闭疏窗,沉思往事立残阳。 被酒莫惊春睡重,赌书消得泼茶香,当时只道是寻常。 记得年轻时学这篇词,就是愣背,现在也就记得这句当时只道是寻常…...
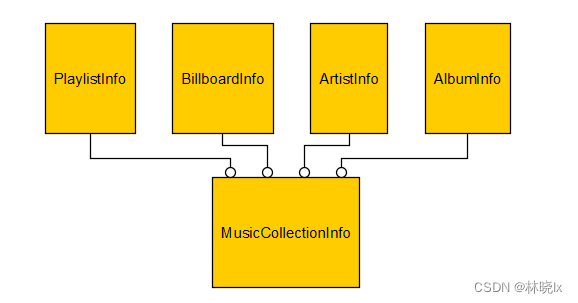
深入解读.NET MAUI音乐播放器项目(一):概述与架构
系列文章将分步解读音乐播放器核心业务及代码: 深入解读.NET MAUI音乐播放器项目(一):概述与架构深入解读.NET MAUI音乐播放器项目(二):播放内核深入解读.NET MAUI音乐播放器项目(三…...

【Python小游戏】某程序员将套圈游戏玩儿到了巅峰,好嗨哟~Pygame代码版《牛牛套圈》已上线,大人的套圈游戏太嗨了,小孩勿进。
前言 世上选择那么多。 关注栗子同学会是您最明智的选择哦。 所有文章完整的素材源码都在👇👇 粉丝白嫖源码福利,请移步至CSDN社区或文末公众hao即可免费。 “幸运牛牛套圈圈”套住欢乐,圈住幸福,等你来挑战…...

php的declare命令如何使用?
php中的declare结构用来设定一段代码的执行指令declare用于执行3个指令:ticks,encoding,strict_typesdeclare结构用于全局范围,影响到其后的所有代码(但如果有declare结构的文件被其他文件包含,则对包含他的父文件不起作用&#x…...
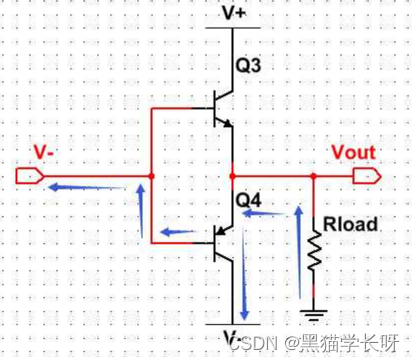
嵌软工程师要掌握的硬件知识2:一文看懂什么开漏和推挽电路(open-drain / push-pull)
想了解开漏和推挽,就要先了解一下三极管和场效应管是什么,在其他章节有详细介绍,本文就不再进行赘述。 1 推挽(push pull)电路 1.1 理解什么是推挽电路 - 详细介绍 如图所示,Q3是个NPN型三极管,Q4是个PNP型三极管。 1)当Vin电压为正时,上面的N型三极管控制端有电…...

1.2.6存储结构-磁盘管理:单缓冲区与双缓冲区读取、流水线周期、计算流水线执行时间
1.2.6存储结构-磁盘管理:单缓冲区与双缓冲区读取、流水线周期、计算流水线执行时间流水线周期计算流水线执行时间微秒,时间单位,符号μs(英语:microsecond ),1微秒等于百万分之一秒(…...

【pytest接口自动化测试】结合单元测试框架pytest+数据驱动模型+allure
api: 存储测试接口 conftest.py :设置前置操作 目前前置操作:1、获取token并传入headers,2、获取命令行参数给到环境变量,指定运行环境commmon:存储封装的公共方法 connect_mysql.py:连接数据库http_requests.py: 封装…...

展锐平台WIFI吞吐问题解决方案
同学,别退出呀,我可是全网最牛逼的 WIFI/BT/GPS/NFC分析博主,我写了上百篇文章,请点击下面了解本专栏,进入本博主主页看看再走呗,一定不会让你后悔的,记得一定要去看主页置顶文章哦。 一、Wi-Fi 吞吐验收标准 预置条件:屏蔽房;DUT 距离 AP 1m 左右;测试 AP 不加密;…...

全局向量的词嵌入(GloVe)
诸如词-词共现计数的全局语料库统计可以来解释跳元模型。 交叉熵损失可能不是衡量两种概率分布差异的好选择,特别是对于大型语料库。GloVe使用平方损失来拟合预先计算的全局语料库统计数据。 对于GloVe中的任意词,中心词向量和上下文词向量在数学上是等…...
,真题含思路)
华为OD机试 - 特异性双端队列(Python),真题含思路
特异性双端队列 题目 有一个特异性的双端队列,该队列可以从头部到尾部添加数据,但是只能从头部移除数据。 小 A 一次执行 2 n 2n 2n 个指令往队列中添加数据和移除数据, 其中 n n n 个指令是添加数据(可能从头部也可以从尾部添加) 依次添加 1 到...
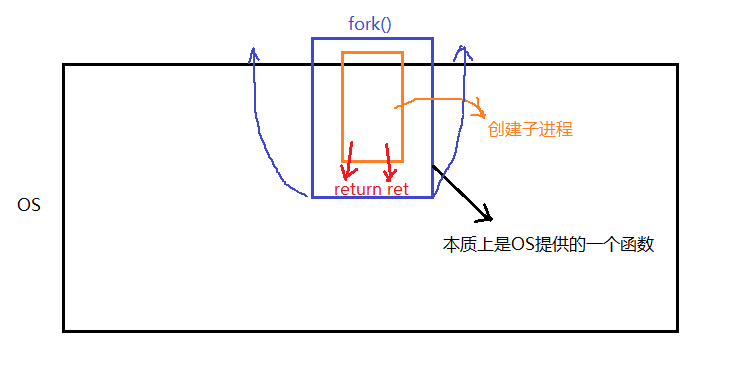
【Linux】操作系统进程概念
文章目录1. 冯诺依曼体系结构2. 操作系统3. 进程进程的基本概念查看进程和杀死进程父进程和子进程通过系统调用创建子进程1. 冯诺依曼体系结构 冯诺依曼结构也称普林斯顿结构,是一种将程序指令存储器和数据存储器合并在一起的存储器结构。数学家冯诺依曼提出了计算…...

C语言const的用法详解
有时候我们希望定义这样一种变量,它的值不能被改变,在整个作用域中都保持固定。例如,用一个变量来表示班级的最大人数,或者表示缓冲区的大小。为了满足这一要求,可以使用const关键字对变量加以限定:constin…...
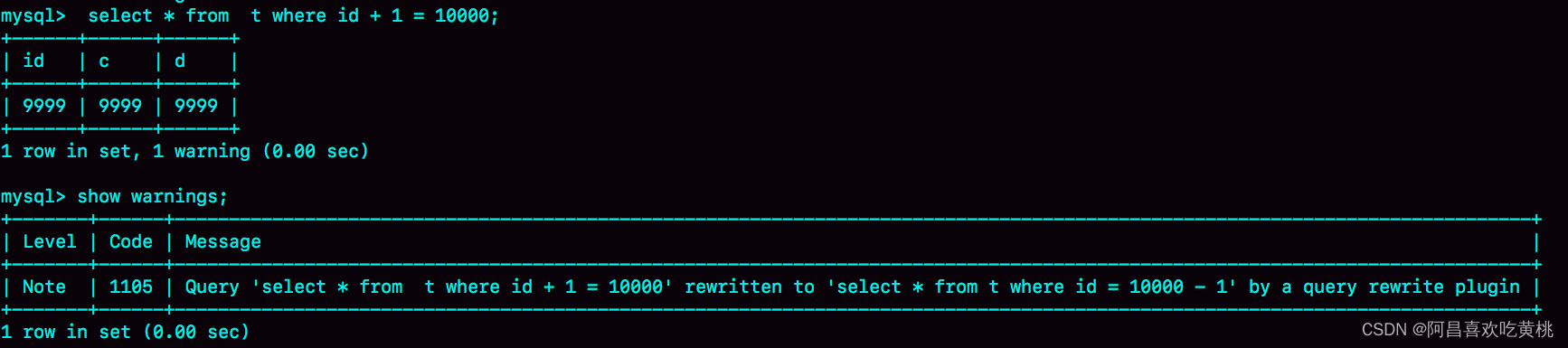
Day886.MySQL的“饮鸩止渴”提高性能的方法 -MySQL实战
MySQL的“饮鸩止渴”提高性能的方法 HI,我是阿昌,今天学习记录的是关于MySQL的“饮鸩止渴”提高性能的方法的内容。 不知道在实际运维过程中有没有碰到这样的情景: 业务高峰期,生产环境的 MySQL 压力太大,没法正常响…...
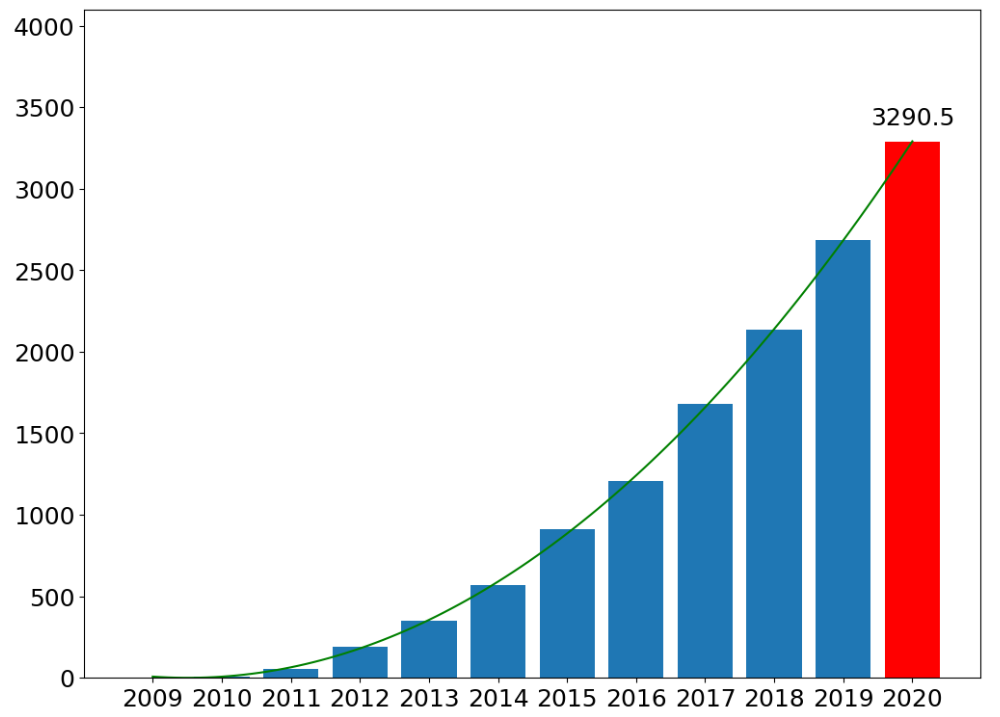
08- 数据升维 (PolynomialFeatures) (机器学习)
在做数据升维的时候,最常见的手段就是将已知维度进行相乘(或者自乘)来构建新的维度 使用 np.concatenate()进行简单的,幂次合并,注意数据合并的方向axis 1 数据可视化时,注意切片,因为数据升维…...
)
2023备战金三银四,Python自动化软件测试面试宝典合集(二)
马上就又到了程序员们躁动不安,蠢蠢欲动的季节~这不,金三银四已然到了家门口,元宵节一过后台就有不少人问我:现在外边大厂面试都问啥想去大厂又怕面试挂面试应该怎么准备测试开发前景如何面试,一个程序员成长之路永恒绕…...

笔试题-2023-紫光展锐-数字芯片设计【纯净题目版】
回到首页:2023 数字IC设计秋招复盘——数十家公司笔试题、面试实录 推荐内容:数字IC设计学习比较实用的资料推荐 题目背景 笔试时间:2022.08.24应聘岗位:数字芯片设计工程师笔试时长:90min笔试平台:nowcoder牛客网题目类型:单选题(18道)、不定项选择题(22道)题目评…...
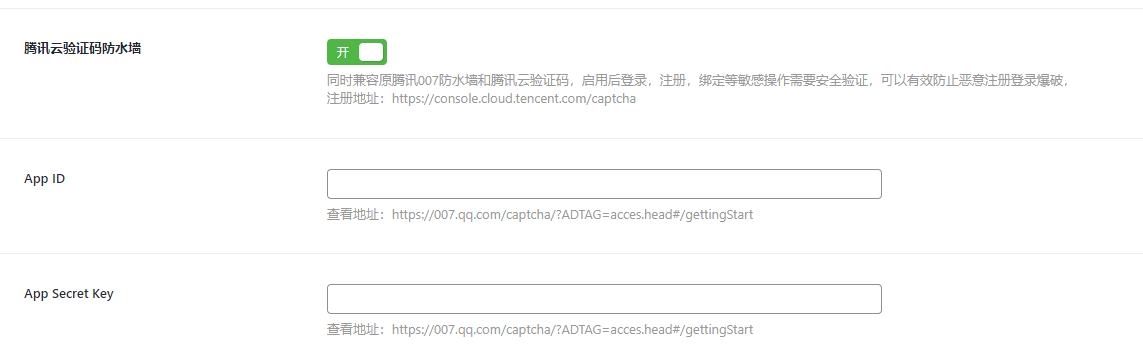
WordPress网站日主题Ri主题RiProV2主题开启了验证码登录但是验证码配置不对结果退出登录后进不去管理端了
背景 WordPress网站日主题Ri主题RiProV2主题开启了验证码登录但是验证码配置不对结果退出登录后进不去管理端了;开启了腾讯云验证码防火墙但APPID,APPSecret没配置,结果在退出登录后,由于验证码验证失败管理端进不去了 提示如下:...

自动驾驶感知——毫米波雷达
文章目录1. 雷达的基本概念1.1 毫米波雷达分类1.2 信息的传输1.3 毫米波雷达的信号频段1.4 毫米波雷达工作原理1.4.1 毫米波雷达测速测距的数学原理1.4.2 毫米波雷达测角度的数学原理1.4.3 硬件接口1.4.4 关键零部件1.4.5 数据的协议与格式1.5 车载毫米波雷达的重要参数1.6 车载…...
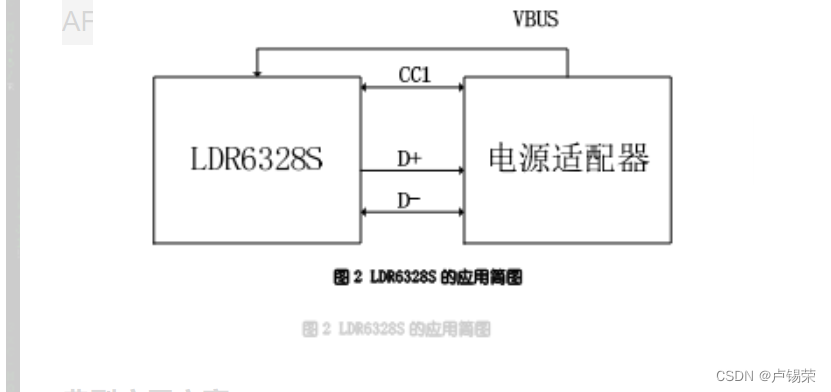
取电芯片全协议都可兼容
乐得瑞PD协议芯片/PD取电芯片/PD受电端协议芯片 支持5/9/12/15/20v定制 1、概述 LDR6328S 是乐得瑞科技有限公司开发的一款兼容 USB PD、QC 和 AFC 协议的 Sink 控制器。 LDR6328S 从支持 USB PD、QC 和 AFC 协议的适配器取电,然后供电给设备。比如可以配置适配器输…...

自己总结优化代码写法
jdk1.7新特性详解 开发期间略知jdk1.7的一些特性,没有真正的一个一个得展开研究,而是需要说明再去查,导致最整个新特性不是特别的清楚,这种情况以后得需要改变了,否则就会变成代码的奴隶。现在正好有时间可以细细的研…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...
