CF1560D Make a Power of Two 题解
CF1560D Make a Power of Two 题解
- 题目
- 链接
- 字面描述
- 题面翻译
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 思路
- 代码实现
- 备注
题目
链接
https://www.luogu.com.cn/problem/CF1560D
字面描述
题面翻译
给定一个整数 nnn。每次操作你可以做两件事情中的一件:
- 删去这个数中的一个数位(如果这个数只剩下一位,则可以把它删空)。
- 在这个数的右边添加一个数位。
你可以以任意顺序执行无限次操作。但请注意,在删去一个数位之后,这个数可能包含前导零(例如在删去 301301301 中的 333 这一位之后,这个数就会变成 010101 而不是 111)。
你需要执行若干次操作,使得这个数最终变成一个 222 的次幂,或者说存在一个非负整数 kkk 使得这个数最终是 2k2^k2k。最终答案不能包含前导零。请求出需要执行的操作的最小次数。
ttt 组数据,1⩽t⩽1041\leqslant t\leqslant 10^41⩽t⩽104,1⩽n⩽1091\leqslant n\leqslant 10^91⩽n⩽109。
题目描述
You are given an integer $ n $ . In $ 1 $ move, you can do one of the following actions:
- erase any digit of the number (it’s acceptable that the number before the operation has exactly one digit and after the operation, it is “empty”);
- add one digit to the right.
The actions may be performed in any order any number of times.
Note that if, after deleting some digit from a number, it will contain leading zeroes, they will not be deleted. E.g. if you delete from the number $ 301 $ the digit $ 3 $ , the result is the number $ 01 $ (not $ 1 $ ).
You need to perform the minimum number of actions to make the number any power of $ 2 $ (i.e. there’s an integer $ k $ ( $ k \ge 0 $ ) such that the resulting number is equal to $ 2^k $ ). The resulting number must not have leading zeroes.
E.g. consider $ n=1052 $ . The answer is equal to $ 2 $ . First, let’s add to the right one digit $ 4 $ (the result will be $ 10524 $ ). Then let’s erase the digit $ 5 $ , so the result will be $ 1024 $ which is a power of $ 2 $ .
E.g. consider $ n=8888 $ . The answer is equal to $ 3 $ . Let’s erase any of the digits $ 8 $ three times. The result will be $ 8 $ which is a power of $ 2 $ .
输入格式
The first line contains one integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. Then $ t $ test cases follow.
Each test case consists of one line containing one integer $ n $ ( $ 1 \le n \le 10^9 $ ).
输出格式
For each test case, output in a separate line one integer $ m $ — the minimum number of moves to transform the number into any power of $ 2 $ .
样例 #1
样例输入 #1
12
1052
8888
6
75
128
1
301
12048
1504
6656
1000000000
687194767
样例输出 #1
2
3
1
3
0
0
2
1
3
4
9
2
提示
The answer for the first test case was considered above.
The answer for the second test case was considered above.
In the third test case, it’s enough to add to the right the digit $ 4 $ — the number $ 6 $ will turn into $ 64 $ .
In the fourth test case, let’s add to the right the digit $ 8 $ and then erase $ 7 $ and $ 5 $ — the taken number will turn into $ 8 $ .
The numbers of the fifth and the sixth test cases are already powers of two so there’s no need to make any move.
In the seventh test case, you can delete first of all the digit $ 3 $ (the result is $ 01 $ ) and then the digit $ 0 $ (the result is $ 1 $ ).
思路
本题最终的目的是将一个[1,1e9]的整数通过2种操作变为2的非负整数次幂。
将20 - 255 每一个数位上的数打表预处理,用原数列一一与表中元素比较,计算操作次数,记录最小值。
时间复杂度: O(10t)≈1e5O(10t)≈1e5O(10t)≈1e5
代码实现
#include<bits/stdc++.h>
#define ll long long
using namespace std;const int maxn=100;
const int inf=2e9;
int t,ans=inf,tot;
ll op=1,x;
ll a[maxn];
int k[maxn];//记录表中每一元素的长度
ll cnt[maxn][maxn];
int main(){//预处理++k[0];cnt[0][1]=1;for(int i=1;i<=55;i++){op=(ll)op*2;ll op1=op;while(op1){cnt[i][++k[i]]=(ll)op1%10;op1=(ll)op1/10;}}/*for(int i=1;i<=40;i++){for(int j=k[i];j>=1;j--)printf("%lld",cnt[i][j]);printf("\n");}*/scanf("%d",&t);while(t--){ans=inf;scanf("%lld",&x);tot=0;while(x){a[++tot]=(ll)x%10;x=(ll)x/10;}//for(int i=tot;i>=1;i--)printf("%d",a[i]);//计算比较for(int i=0;i<=55;i++){int st1=tot,st2=k[i];while(st1>0&&st2>0){if(a[st1]==cnt[i][st2])--st2;--st1;}//if(i==41)printf("41 %d %d\n",k[i],st2);ans=min(ans,tot-k[i]+2*st2);// tot-(k[i]-st2) 删除的操作次数操作次数 & st2 添加的操作次数}printf("%d\n",ans);}return 0;
}
备注
写入好题本
相关文章:

CF1560D Make a Power of Two 题解
CF1560D Make a Power of Two 题解题目链接字面描述题面翻译题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示思路代码实现备注题目 链接 https://www.luogu.com.cn/problem/CF1560D 字面描述 题面翻译 给定一个整数 nnn。每次操作你可以做两件事情中的一件&am…...

C#开发的OpenRA的读取文件的函数
C#开发的OpenRA的读取文件的函数 在OpenRA游戏里,读取文件是必备的功能。 因为游戏大部分文件都是图片、动画、语音。 很久以前,我以为开发游戏的主要功能是在程序开发上, 其实游戏的大部分工作都不是在开发上,而是在美工方面。 因为游戏跟电影是一样,就是不断地展示场景,…...

SpringBoot结合XXL-JOB实现定时任务
Quartz的不足 Quartz 的不足:Quartz 作为开源任务调度中的佼佼者,是任务调度的首选。但是在集群环境中,Quartz采用API的方式对任务进行管理,这样存在以下问题: 通过调用API的方式操作任务,不人性化。需要…...

【Node.js】 创建web服务器
Node.js什么是客户端,什么是服务器服务器和普通电脑的区别什么是http模块导入http模块服务器相关概念创建web服务器的基本步骤req请求对象req响应对象解决中文乱码根据不同的url响应不同的html内容什么是客户端,什么是服务器 客户端在网络节点中&#x…...

基于go语言实现RestFul交互
一、RestFul 1.1 RestFul的介绍 RESTFUL(Representational State Transfer)是一种网络应用程序的设计风格和开发方式,基于HTTP或HTTPS,可以使用XML格式定义或JSON格式定义。RESTFUL适用于移动互联网厂商作为业务接口的场景&…...

情感溢出:读《浣溪沙》
浣溪沙 谁念西风独自凉 作者 纳兰性德 谁念西风独自凉,萧萧黄叶闭疏窗,沉思往事立残阳。 被酒莫惊春睡重,赌书消得泼茶香,当时只道是寻常。 记得年轻时学这篇词,就是愣背,现在也就记得这句当时只道是寻常…...
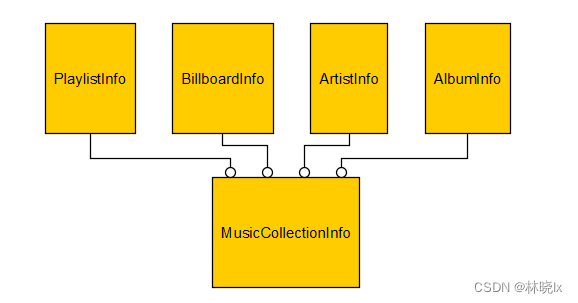
深入解读.NET MAUI音乐播放器项目(一):概述与架构
系列文章将分步解读音乐播放器核心业务及代码: 深入解读.NET MAUI音乐播放器项目(一):概述与架构深入解读.NET MAUI音乐播放器项目(二):播放内核深入解读.NET MAUI音乐播放器项目(三…...

【Python小游戏】某程序员将套圈游戏玩儿到了巅峰,好嗨哟~Pygame代码版《牛牛套圈》已上线,大人的套圈游戏太嗨了,小孩勿进。
前言 世上选择那么多。 关注栗子同学会是您最明智的选择哦。 所有文章完整的素材源码都在👇👇 粉丝白嫖源码福利,请移步至CSDN社区或文末公众hao即可免费。 “幸运牛牛套圈圈”套住欢乐,圈住幸福,等你来挑战…...

php的declare命令如何使用?
php中的declare结构用来设定一段代码的执行指令declare用于执行3个指令:ticks,encoding,strict_typesdeclare结构用于全局范围,影响到其后的所有代码(但如果有declare结构的文件被其他文件包含,则对包含他的父文件不起作用&#x…...
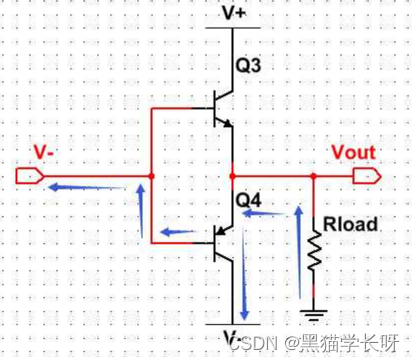
嵌软工程师要掌握的硬件知识2:一文看懂什么开漏和推挽电路(open-drain / push-pull)
想了解开漏和推挽,就要先了解一下三极管和场效应管是什么,在其他章节有详细介绍,本文就不再进行赘述。 1 推挽(push pull)电路 1.1 理解什么是推挽电路 - 详细介绍 如图所示,Q3是个NPN型三极管,Q4是个PNP型三极管。 1)当Vin电压为正时,上面的N型三极管控制端有电…...

1.2.6存储结构-磁盘管理:单缓冲区与双缓冲区读取、流水线周期、计算流水线执行时间
1.2.6存储结构-磁盘管理:单缓冲区与双缓冲区读取、流水线周期、计算流水线执行时间流水线周期计算流水线执行时间微秒,时间单位,符号μs(英语:microsecond ),1微秒等于百万分之一秒(…...

【pytest接口自动化测试】结合单元测试框架pytest+数据驱动模型+allure
api: 存储测试接口 conftest.py :设置前置操作 目前前置操作:1、获取token并传入headers,2、获取命令行参数给到环境变量,指定运行环境commmon:存储封装的公共方法 connect_mysql.py:连接数据库http_requests.py: 封装…...

展锐平台WIFI吞吐问题解决方案
同学,别退出呀,我可是全网最牛逼的 WIFI/BT/GPS/NFC分析博主,我写了上百篇文章,请点击下面了解本专栏,进入本博主主页看看再走呗,一定不会让你后悔的,记得一定要去看主页置顶文章哦。 一、Wi-Fi 吞吐验收标准 预置条件:屏蔽房;DUT 距离 AP 1m 左右;测试 AP 不加密;…...

全局向量的词嵌入(GloVe)
诸如词-词共现计数的全局语料库统计可以来解释跳元模型。 交叉熵损失可能不是衡量两种概率分布差异的好选择,特别是对于大型语料库。GloVe使用平方损失来拟合预先计算的全局语料库统计数据。 对于GloVe中的任意词,中心词向量和上下文词向量在数学上是等…...
,真题含思路)
华为OD机试 - 特异性双端队列(Python),真题含思路
特异性双端队列 题目 有一个特异性的双端队列,该队列可以从头部到尾部添加数据,但是只能从头部移除数据。 小 A 一次执行 2 n 2n 2n 个指令往队列中添加数据和移除数据, 其中 n n n 个指令是添加数据(可能从头部也可以从尾部添加) 依次添加 1 到...
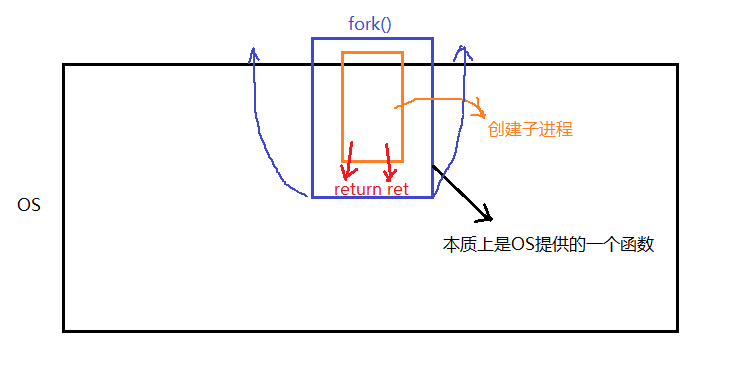
【Linux】操作系统进程概念
文章目录1. 冯诺依曼体系结构2. 操作系统3. 进程进程的基本概念查看进程和杀死进程父进程和子进程通过系统调用创建子进程1. 冯诺依曼体系结构 冯诺依曼结构也称普林斯顿结构,是一种将程序指令存储器和数据存储器合并在一起的存储器结构。数学家冯诺依曼提出了计算…...

C语言const的用法详解
有时候我们希望定义这样一种变量,它的值不能被改变,在整个作用域中都保持固定。例如,用一个变量来表示班级的最大人数,或者表示缓冲区的大小。为了满足这一要求,可以使用const关键字对变量加以限定:constin…...
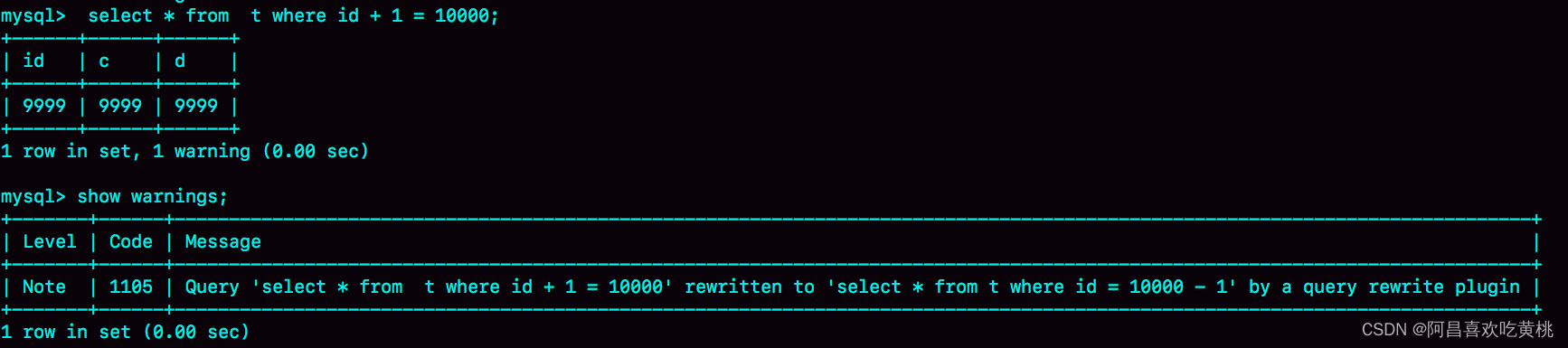
Day886.MySQL的“饮鸩止渴”提高性能的方法 -MySQL实战
MySQL的“饮鸩止渴”提高性能的方法 HI,我是阿昌,今天学习记录的是关于MySQL的“饮鸩止渴”提高性能的方法的内容。 不知道在实际运维过程中有没有碰到这样的情景: 业务高峰期,生产环境的 MySQL 压力太大,没法正常响…...
08- 数据升维 (PolynomialFeatures) (机器学习)
在做数据升维的时候,最常见的手段就是将已知维度进行相乘(或者自乘)来构建新的维度 使用 np.concatenate()进行简单的,幂次合并,注意数据合并的方向axis 1 数据可视化时,注意切片,因为数据升维…...
)
2023备战金三银四,Python自动化软件测试面试宝典合集(二)
马上就又到了程序员们躁动不安,蠢蠢欲动的季节~这不,金三银四已然到了家门口,元宵节一过后台就有不少人问我:现在外边大厂面试都问啥想去大厂又怕面试挂面试应该怎么准备测试开发前景如何面试,一个程序员成长之路永恒绕…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...

MeshGPT 笔记
[2311.15475] MeshGPT: Generating Triangle Meshes with Decoder-Only Transformers https://library.scholarcy.com/try 真正意义上的AI生成三维模型MESHGPT来袭!_哔哩哔哩_bilibili GitHub - lucidrains/meshgpt-pytorch: Implementation of MeshGPT, SOTA Me…...

Appium下载安装配置保姆教程(图文详解)
目录 一、Appium软件介绍 1.特点 2.工作原理 3.应用场景 二、环境准备 安装 Node.js 安装 Appium 安装 JDK 安装 Android SDK 安装Python及依赖包 三、安装教程 1.Node.js安装 1.1.下载Node 1.2.安装程序 1.3.配置npm仓储和缓存 1.4. 配置环境 1.5.测试Node.j…...
