最优化方法Python计算:无约束优化应用——神经网络回归模型
人类大脑有数百亿个相互连接的神经元(如下图(a)所示),这些神经元通过树突从其他神经元接收信息,在细胞体内综合、并变换信息,通过轴突上的突触向其他神经元传递信息。我们在博文《最优化方法Python计算:无约束优化应用——逻辑回归模型》中讨论的逻辑回归模型(如下图(b)所示)与神经元十分相似,由输入端接收数据 x = ( x 1 x 2 ⋮ x n ) \boldsymbol{x}=\begin{pmatrix} x_1\\x_2\\\vdots\\x_n \end{pmatrix} x= x1x2⋮xn ,作加权和 ∑ i = 1 n w i x i \sum\limits_{i=1}^nw_ix_i i=1∑nwixi加上偏移量 b b b,即 ∑ i = 1 n w i x i + b \sum\limits_{i=1}^nw_ix_i+b i=1∑nwixi+b,用逻辑函数将其映射到区间 ( 0 , 1 ) (0,1) (0,1)内,然后将如此变换所得的信息 y y y输出。

这启发人们将诸多逻辑回归模型分层连接起来,构成人工神经网络,创建出多层感应模型。下图展示了一个包括输入层、输出层和两个隐藏层(图中阴影部分)的人工神经网络。图中,黑点表示数据节点,圆圈表示人工神经元的处理节点。

记逻辑函数 sigmoid ( x ) = 1 1 + e − x = φ ( x ) \text{sigmoid}(x)=\frac{1}{1+e^{-x}}=\varphi(x) sigmoid(x)=1+e−x1=φ(x)。设多层感应模型的输入数据为 n n n维向量 x = ( x 1 x 2 ⋮ x n ) \boldsymbol{x}=\begin{pmatrix} x_1\\x_2\\\vdots\\x_n \end{pmatrix} x= x1x2⋮xn 。不算输入层,模型连同输出层及隐藏层共有 l l l层。记 m 0 = n m_0=n m0=n,第 i i i层( 0 < i ≤ l 0<i\leq l 0<i≤l)含有 m i m_i mi个神经元。于是,相邻的两层,第 i − 1 i-1 i−1和第 i i i之间共有 ( m i − 1 + 1 ) m i (m_{i-1}+1)m_{i} (mi−1+1)mi个待定参数。因此,模型具有
p = ∑ i = 1 l ( m i − 1 + 1 ) m i p=\sum_{i=1}^l(m_{i-1}+1)m_i p=i=1∑l(mi−1+1)mi
个待定参数,组织成 p p p维向量 w = ( w 1 w 2 ⋮ w p ) \boldsymbol{w}=\begin{pmatrix} w_1\\w_2\\\vdots\\w_p \end{pmatrix} w= w1w2⋮wp 。设 k 0 = 0 k_0=0 k0=0,对 1 < i ≤ l 1<i\leq l 1<i≤l, k i = ∑ t = 0 i − 1 ( m t + 1 ) m t + 1 k_i=\sum\limits_{t=0}^{i-1}(m_{t}+1)m_{t+1} ki=t=0∑i−1(mt+1)mt+1,记 ( m i − 1 − 1 ) × m i (m_{i-1}-1)\times m_i (mi−1−1)×mi矩阵
w i = ( w k i + 1 ⋯ w k i + ( m i − 1 + 1 ) ( m i − 1 ) + 1 ⋮ ⋱ ⋮ w k i + ( m i − 1 + 1 ) ⋯ w k i + ( m i − 1 + 1 ) m i ) , i = 1 , 2 ⋯ , l \boldsymbol{w}_i=\begin{pmatrix} w_{k_i+1}&\cdots&w_{k_i+(m_{i-1}+1)(m_i-1)+1}\\ \vdots&\ddots&\vdots\\ w_{k_i+(m_{i-1}+1)}&\cdots&w_{k_i+(m_{i-1}+1)m_i} \end{pmatrix}, i=1,2\cdots,l wi= wki+1⋮wki+(mi−1+1)⋯⋱⋯wki+(mi−1+1)(mi−1)+1⋮wki+(mi−1+1)mi ,i=1,2⋯,l
定义函数
F ( w ; x ) = φ ( ( ⋯ φ ⏟ l ( ( x ⊤ , 1 ) w 1 ) , 1 ) , ⋯ ) , 1 ) w l ) . F(\boldsymbol{w};\boldsymbol{x})=\underbrace{\varphi((\cdots\varphi}_l((\boldsymbol{x}^\top,1)\boldsymbol{w}_1),1),\cdots),1)\boldsymbol{w}_l). F(w;x)=l φ((⋯φ((x⊤,1)w1),1),⋯),1)wl).
该函数反映了数据从输入层到输出层的传输方向,称为前向传播函数,作为多层感应模型的拟合函数。按此定义,我们构建如下的多层感应模型类
import numpy as np #导入numpy
class MLPModel(LogicModel): #多层感应模型def construct(self, X, hidden_layer_sizes): #确定网络结构if len(X.shape)==1: #计算输入端节点数k = 1else:k = X.shape[1]self.layer_sizes = (k,)+hidden_layer_sizes+(1,) def patternlen(self): #模式长度p = 0l = len(self.layer_sizes) #总层数for i in range(l-1): #逐层累加m = self.layer_sizes[i]n = self.layer_sizes[i+1]p += (m+1)*nreturn pdef F(self, w, x): #拟合函数l = len(self.layer_sizes) #总层数m, n = self.layer_sizes[0],self.layer_sizes[1]k = (m+1)*n #第0层参数个数W = w[0:k].reshape(m+1,n) #0层参数折叠为矩阵z = LogicModel.F(self, W, x) #第1层的输入for i in range(1, l-1): #逐层计算m = self.layer_sizes[i] #千层节点数n = self.layer_sizes[i+1] #后层节点数W = w[k:k+(m+1)*n].reshape(m+1,n) #本层参数矩阵z = np.hstack((z, np.ones(z.shape[0]). #本层输入矩阵reshape(z.shape[0], 1)))z = LogicModel.F(self, W, z) #下一层输入k += (m+1)*n #下一层参数下标起点y = z.flatten() #展平输出return ydef fit(self, X, Y, w = None, hidden_layer_sizes = (100,)): #重载训练函数self.construct(X, hidden_layer_sizes)LogicModel.fit(self, X, Y, w)
class MLPRegressor(Regression, MLPModel):'''神经网络回归模型'''
MLPModel继承了LogicModel类(详见博文《最优化方法Python计算:无约束优化应用——逻辑回归模型》)在MLPModel中除了重载模式长度计算函数patternlen、拟合函数F和训练函数fit外,增加了一个LogicModel类所没有的对象函数construct,用来确定神经网络的结构:有少层,各层有多少个神经元。
具体而言,第3~8行的construct函数,利用传递给它的输入矩阵X和隐藏层结构hidden_layer_sizes,这是一个元组,计算神经网络的各层结构。第4~7行的if-else分支按输入数据X的形状确定输入层的节点数k。第8行将元组(k,1)和(1,)分别添加在hidden_layer_sizes的首尾两端,即确定了网络结构layer_sizes。
第9~16行重载了模式长度计算函数patternlen。第11行根据模型的结构元组layer_sizes的长度确定层数l。第12~15行的for循环组成计算各层的参数个数:m为前层节点数(第13行),n为后层节点数(第14行),则第15行中(m+1)*n就是本层的参数个数,这是因为后层的每个节点的输入必须添加一个偏移量。第16行将算得的本层参数个数累加到总数p(第10行初始化为0)。
第17~32行重载拟合函数F,参数中w表示模式 w ∈ R p \boldsymbol{w}\in\text{R}^p w∈Rp,x表示自变量 ( x ⊤ , 1 ) (\boldsymbol{x}^\top,1) (x⊤,1)。第18行读取网络层数l。第19~22行计算第1隐藏层的输入:第19行读取第0层节点数m第1隐藏层节点数n。第20行计算第0层参数个数k(也是第1层参数下标起点)。第22行构造第0层的参数矩阵W。第22行计算 φ ( ( x ⊤ , 1 ) w 1 ) \varphi((\boldsymbol{x}^\top,1)\boldsymbol{w}_1) φ((x⊤,1)w1),作为第1隐藏层的输入z。第23~20行的for循环依次逐层构造本层参数矩阵 w i \boldsymbol{w}_i wi(第26行)和输入 ( z i ⊤ , 1 ) (\boldsymbol{z}_i^\top,1) (zi⊤,1)(第27~28行),第30行计算下一层的输入 φ ( ( z i ⊤ , 1 ) w i ) \varphi((\boldsymbol{z}_i^\top,1)\boldsymbol{w}_i) φ((zi⊤,1)wi)为z,第30行更新下一层参数下标起点k。完成循环,所得y因为是矩阵运算的结果,第31层将其扁平化为一维数组。第33~35行重载训练函数fit。与其祖先LogicModel的(也是LineModel)fit函数相比,多了一个表示网络结构的参数hidden_layer_sizes。如前所述,这是一个元组,缺省值为(100,),意味着只有1个隐藏层,隐藏层含100个神经元。函数体内第34行调用自身的construct函数,构造网络结构layer_sizes,供调用拟合函数F时使用。第35行调用祖先LogicModel的fit函数完成训练。
第36~37用Regression类和MLPModel类联合构成用于预测的多层感应模型类MLPRegressor。
理论上,只要给定足够多的隐藏层和层内所含神经元,多层感应模型能拟合任意函数。
例1 用MLPRegressor对象拟合函数 y = x 2 y=x^2 y=x2。
解:先构造训练数据:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import uniform
np.random.seed(2023)
x = uniform.rvs(-1, 2, 50)
y = (x**2)
plt.scatter(x, y)
plt.show()
第5行产生50个服从均匀分布 U ( 0 , 1 ) U(0,1) U(0,1)的随机数值,赋予x。第6行计算x的平方赋予y。第7行绘制 ( x , y ) (x,y) (x,y)散点图。

用仅含一个隐藏层,隐藏层中包含3个神经元的多层感应器拟合 y = x 2 y=x^2 y=x2
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import uniform
.random.seed(2023)
x = uniform.rvs(-1, 2, 50)
y = (x**2)
nnw = MLPRegressor()
nnw.fit(x,y,hidden_layer_sizes = (3,))
yp, acc = nnw.test(x, y)
plt.scatter(x, yp)
plt.show()
print('1隐藏层含3个神经元网络拟合均方根误差%.4f'%acc)
前5行与前同。第6行创建MLPRegressor类对象nnw。第7行用x,y训练nnw为含1个隐藏层,隐藏层含3个神经元的神经网络。第8行调用nnw的test函数,用返回的yp绘制 ( x , y p ) (x,y_p) (x,yp)散点图。

训练中...,稍候
726次迭代后完成训练。
1隐藏层含3个神经元网络拟合均方根误差0.0238
用含两个隐藏层,分别包含7个、3个神经元的多层感应器拟合 y = x 2 y=x^2 y=x2
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import uniform
.random.seed(2023)
x = uniform.rvs(-1, 2, 50)
y = (x**2)
nnw = MLPRegressor()
nnw.fit(x, y, hidden_layer_sizes = (7, 3))
yp, acc = nnw.test(x,y)
plt.scatter(x, yp)
plt.show()
print('2隐藏层含各7,3个神经元网络拟合方根误差%.4f'%acc)
与上一段代码比较,仅第8行训练nnw的网络换成两个隐藏层,分别包含7个、3个神经元的多层感应器。运行程序,输出

训练中...,稍候
1967次迭代后完成训练。
2隐藏层含各7,3个神经元网络拟合方根误差0.0053
比前一个显然拟合得更好,但也付出了计算时间的代价。
Say good bye, 2023.
相关文章:

最优化方法Python计算:无约束优化应用——神经网络回归模型
人类大脑有数百亿个相互连接的神经元(如下图(a)所示),这些神经元通过树突从其他神经元接收信息,在细胞体内综合、并变换信息,通过轴突上的突触向其他神经元传递信息。我们在博文《最优化方法Python计算:无约…...

Spring Data Redis对象缓存序列化问题
相信在项目中,你一定是经常使用 Redis ,那么,你是怎么使用的呢?在使用时,有没有遇到同我一样,对象缓存序列化问题的呢?那么,你又是如何解决的呢? Redis 使用示例 添加依…...

自动驾驶代客泊车AVP巡航规划详细设计
目 录 巡航规划详细设计... 1 修改记录... 2 目 录... 3 1 背景... 5 2 系统环境... 6 2.1 巡航规划与其它模块联系... 6 2.2 巡航规划接口说明... 6 3 规划模块设计... 9 3.1 巡航规划架构图... 9 3.2 预处理... 10 3.3 Planner. 10 3.3.1 Geometry planner. 10 …...
亚马逊云科技 re:Invent 2023 产品体验:亚马逊云科技产品应用实践 国赛选手带你看 Elasticache Serverless
抛砖引玉 讲一下作者背景,曾经参加过国内世界技能大赛云计算的选拔,那么在竞赛中包含两类,一类是架构类竞赛,另一类就是 TroubleShooting 竞赛,对应的分别为亚马逊云科技 GameDay 和亚马逊云科技 Jam,想必…...

Flink on K8S集群搭建及StreamPark平台安装
1.环境准备 1.1 介绍 在使用 Flink&Spark 时发现从编程模型, 启动配置到运维管理都有很多可以抽象共用的地方, 目前streampark提供了一个flink一站式的流处理作业开发管理平台, 从流处理作业开发到上线全生命周期都做了支持, 是一个一站式的流出来计算平台。 未来spark开…...

SpringBoot如何优雅的处理免登录接口
在项目开发过程中,会有很多API接口不需要登录就能直接访问,比如公开数据查询之类的 ~ 常规处理方法基本是 使用拦截器或过滤器,拦截需要认证的请求路径。在拦截器中判断session或token信息,如果存在则放行,否则跳转到…...

元旦档首日票房超4.69亿,“下雪场尴尬”上热搜!
哇塞,元旦假期终于来啦!🎉在这个喜庆的时刻,电影院也热闹非凡,据猫眼专业版数据显示,截至12月30日,2023年元旦档首日票房竟然超过了4.69亿!这简直是个天文数字啊!&#x…...

CentOS系统中设置IP地址的方式和存在的问题
在CentOS系统中设置IP地址通常涉及以下步骤: 打开网络接口配置文件: 使用文本编辑器(如vi、nano或emacs)打开 /etc/sysconfig/network-scripts/ifcfg-eth0 文件。这里的"eth0"是网卡的名称,如果你的系统中有…...
使用vmware,在ubuntu18.04中使用笔记本的摄像头
步骤1:在windows中检查相机状态 win10系统中,在左下的搜索栏,搜索“相机”,点击进入即可打开相机,并正常显示图像。 注意:如果相机连接到了虚拟机,则不能显示正常。 步骤2:在ubuntu…...

中间件系列 - Redis入门到实战(高级篇-分布式缓存)
前言 学习视频: 黑马程序员Redis入门到实战教程,深度透析redis底层原理redis分布式锁企业解决方案黑马点评实战项目 中间件系列 - Redis入门到实战 本内容仅用于个人学习笔记,如有侵扰,联系删除 学习目标 Redis持久化Redis主从…...
使用Visual Studio调试VisionPro脚本
使用Visual Studio调试VisionPro脚本 方法一 : 修改项目文件 csproj步骤: 方法二 : Visual Studio附加功能步骤: 方法一 : 修改项目文件 csproj 步骤: 开启VisionPro脚本调试功能 创建一个VisionPro程序…...
Ubuntu安装K8S的dashboard(管理页面)
原文网址:Ubuntu安装k8s的dashboard(管理页面)-CSDN博客 简介 本文介绍Ubuntu安装k8s的dashboard(管理页面)的方法。 Dashboard的作用有:便捷操作、监控、分析、概览。 相关网址 官网地址:…...
zookeeper之集群搭建
1. 集群角色 zookeeper集群下,有3种角色,分别是领导者(Leader)、跟随着(Follower)、观察者(Observer)。接下来我们分别看一下这三种角色的作用。 领导者(Leader): 事务请求(写操作)的唯一调度者和处理者,保…...

从0开始界面设计师 Qt Designer
QT程序界面的 一个个窗口、控件,就是像上面那样用相应的代码创建出来的。 但是,把你的脑海里的界面,用代码直接写出来,是有些困难的。 很多时候,运行时呈现的样子,不是我们要的。我们经常还要修改代码调整界…...
Html / CSS刷题笔记
WebKit是一个开源的浏览器引擎,它最初是由苹果公司开发的,并且被广泛用于Safari浏览器和其他基于WebKit的浏览器,比如Google Chrome的早期版本。它也是构建许多移动设备浏览器的基础。WebKit的主要功能是解析HTML和CSS,并将其渲染…...
关于“Python”的核心知识点整理大全51
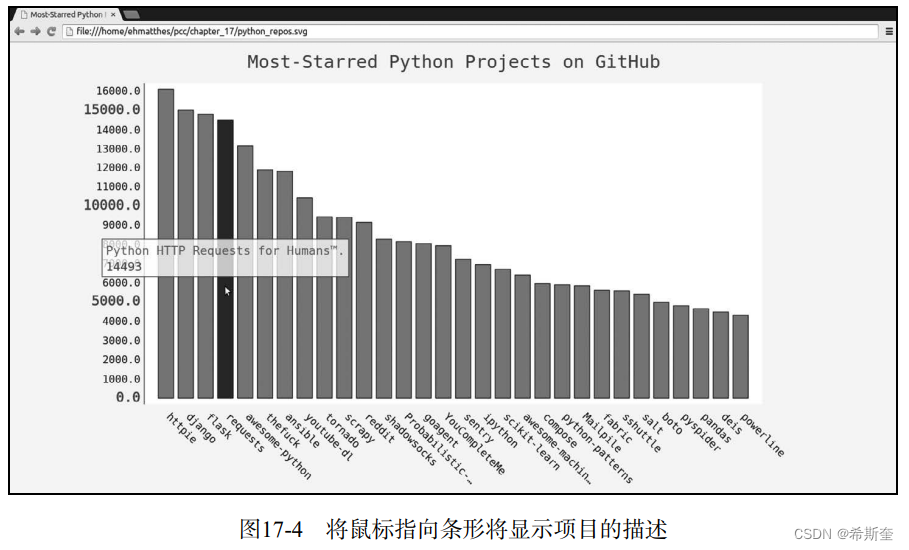
目录 17.2.2 添加自定义工具提示 bar_descriptions.py 17.2.3 根据数据绘图 python_repos.py 17.2.4 在图表中添加可单击的链接 python_repos.py 17.3 Hacker News API hn_submissions.py 17.4 小结 往期快速传送门👆(在文章最后)&a…...
Termius for Mac/Win:一站式终端模拟器、SSH 和 SFTP 客户端软件的卓越选择
随着远程工作和云技术的普及,对于高效安全的远程访问和管理服务器变得至关重要。Termius,一款强大且易用的终端模拟器、SSH 和 SFTP 客户端软件,正是满足这一需求的理想选择。 Termius 提供了一站式的解决方案,允许用户通过单一平…...
vr体验馆用什么软件计时计费,如遇到停电软件程序如何恢复时间
vr体验馆用什么软件计时计费,如遇到停电软件程序如何恢复时间 一、软件程序问答 如下图,软件以 佳易王vr体验馆计时计费软件V17.9为例说明 1、软件如何计时间? 点击相应编号的开始计时按钮即可 2、遇到停电再打开软件时间可以恢复吗&…...

HTML---JavaScript基础
文章目录 目录 文章目录 本章目标 一.JavaScript基础 概述 特点 JavaScript 基本机构 语法 网页中引用JavaScript的方式 二. JavaScript核心语法 变量 编辑 数据类型 数组 练习 本章目标 掌握JavaScript的组成掌握JavaScript的基本语法会定义和使用函数会使用工具进行…...

2023年03月17日_微软和谷歌办公AI的感慨
2023年3月17日 最近这个科技圈的消息 有点爆炸的让人应接不暇了 各种大公司简直就是神仙打架 你从来没有见过这么密集的 这么高频的产品发布 昨天微软是发布了Office 365 Copilot 在里边提供了大量的AI的功能 然后谷歌呢也发布了这个Google Workspace AI 也是跟365 Cop…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...
