三角函数两角和差公式推导
一.几何推理
1.两角和公式
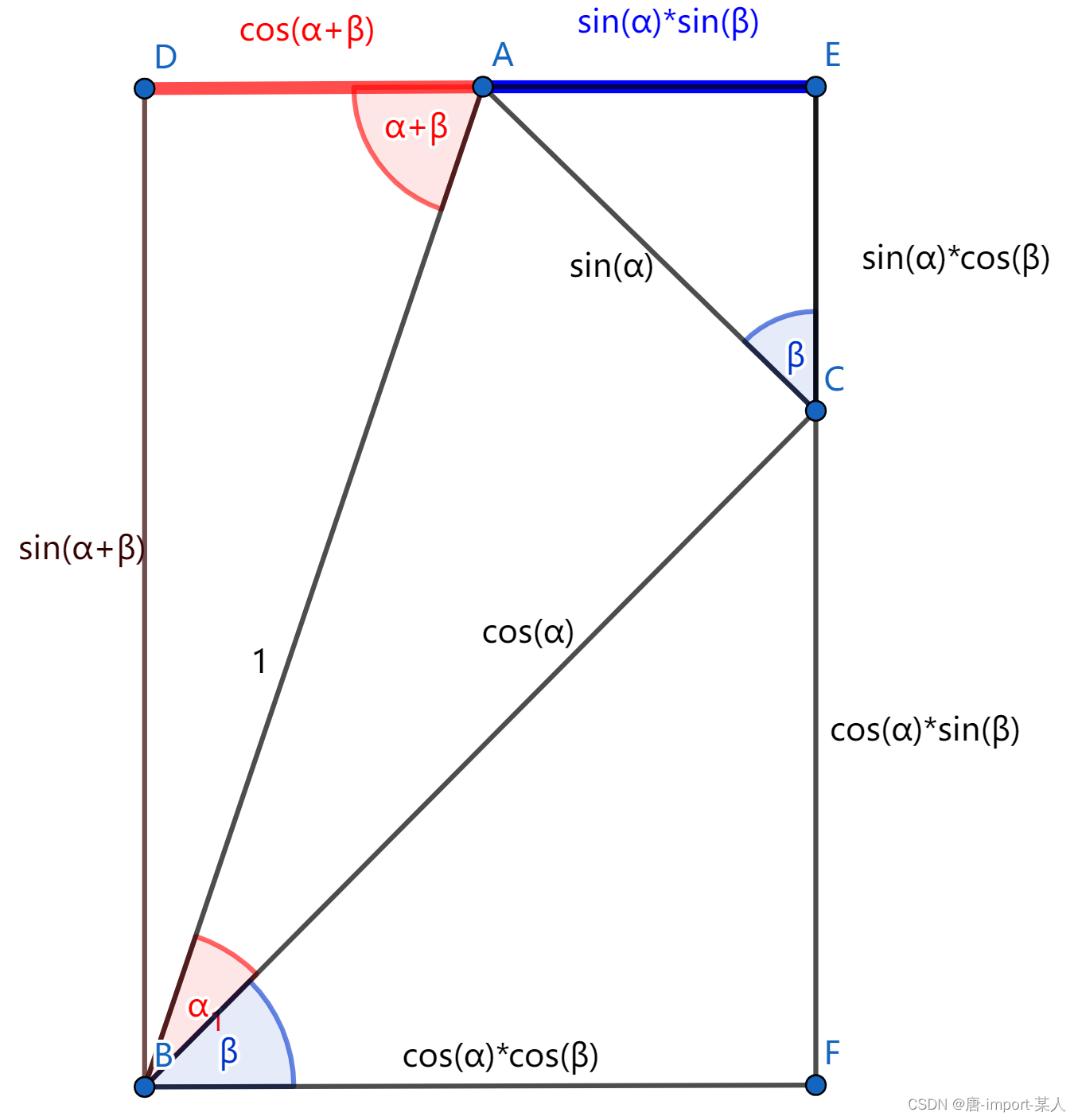
做一斜边为1的直角△ABC,任意旋转非 k Π , k = N kΠ,k=N kΠ,k=N,补充如图,令 ∠ A B C = ∠ α , ∠ C B F = ∠ β ∠ABC=∠α,∠CBF=∠β ∠ABC=∠α,∠CBF=∠β
∴ ∠ D B F = ∠ D B A + ∠ α + ∠ β = 90 ° , ∠ D A F = ∠ D B A + ∠ D A B ∴∠DBF=∠DBA+∠α+∠β=90°,∠DAF=∠DBA+∠DAB ∴∠DBF=∠DBA+∠α+∠β=90°,∠DAF=∠DBA+∠DAB
∵ ∠ D A B = ∠ α + ∠ β ∵∠DAB=∠α+∠β ∵∠DAB=∠α+∠β
∴ ∠ A C F + ∠ B C F = 90 ° ∴∠ACF+∠BCF=90° ∴∠ACF+∠BCF=90°
∵ ∠ A C F = ∠ β ∵∠ACF=∠β ∵∠ACF=∠β
∴ A B 长度为 1 ∴AB长度为1 ∴AB长度为1
∵ A C = s i n ( α ) , B C = c o s ( α ) ∵AC=sin(α),BC=cos(α) ∵AC=sin(α),BC=cos(α)
∵ B F = c o s ( α ) ∗ c o s ( β ) , C F = c o s ( α ) ∗ s i n ( β ) , A E = s i n ( α ) s i n ( β ) , C E = s i n ( α ) c o s ( β ) , B D = E F = s i n ( α + β ) , D A = c o s ( α + β ) ∵BF=cos(α)*cos(β),CF=cos(α)*sin(β),AE=sin(α)sin(β),CE=sin(α)cos(β),BD=EF=sin(α+β),DA=cos(α+β) ∵BF=cos(α)∗cos(β),CF=cos(α)∗sin(β),AE=sin(α)sin(β),CE=sin(α)cos(β),BD=EF=sin(α+β),DA=cos(α+β)
∵ { c o s ( α + β ) = c o s ( α ) ∗ c o s ( β ) − s i n ( α ) ∗ s i n ( β ) s i n ( α + β ) = s i n ( α ) ∗ c o s ( β ) + c o s ( α ) ∗ s i n ( β ) ∵\begin{cases} cos(α+β)=cos(α)*cos(β)-sin(α)*sin(β) \\sin(α+β)=sin(α)*cos(β)+cos(α)*sin(β) \end{cases} ∵{cos(α+β)=cos(α)∗cos(β)−sin(α)∗sin(β)sin(α+β)=sin(α)∗cos(β)+cos(α)∗sin(β)
2.两角差公式
∵ { c o s ( α + β ) = c o s ( α ) ∗ c o s ( β ) − s i n ( α ) ∗ s i n ( β ) s i n ( α + β ) = s i n ( α ) ∗ c o s ( β ) + c o s ( α ) ∗ s i n ( β ) ∵\begin{cases} cos(α+β)=cos(α)*cos(β)-sin(α)*sin(β) \\sin(α+β)=sin(α)*cos(β)+cos(α)*sin(β) \end{cases} ∵{cos(α+β)=cos(α)∗cos(β)−sin(α)∗sin(β)sin(α+β)=sin(α)∗cos(β)+cos(α)∗sin(β)
对 ∠ β 做取反变化 对∠β做取反变化 对∠β做取反变化
∵ { c o s ( α + ( − β ) ) = c o s ( α ) ∗ c o s ( β ) − s i n ( α ) ∗ ( − s i n ( β ) ) s i n ( α + ( − β ) ) = s i n ( α ) ∗ c o s ( β ) + c o s ( α ) ∗ ( − s i n ( β ) ) ∵\begin{cases} cos(α+(-β))=cos(α)*cos(β)-sin(α)*(-sin(β)) \\sin(α+(-β))=sin(α)*cos(β)+cos(α)*(-sin(β)) \end{cases} ∵{cos(α+(−β))=cos(α)∗cos(β)−sin(α)∗(−sin(β))sin(α+(−β))=sin(α)∗cos(β)+cos(α)∗(−sin(β))
∵ { c o s ( α − β ) = s i n ( α ) ∗ s i n ( β ) + c o s ( α ) ∗ s i n ( β ) s i n ( α − β ) = s i n ( α ) ∗ c o s ( β ) − c o s ( α ) ∗ s i n ( β ) ∵\begin{cases} cos(α-β)=sin(α)*sin(β)+cos(α)*sin(β) \\sin(α-β)=sin(α)*cos(β)-cos(α)*sin(β) \end{cases} ∵{cos(α−β)=sin(α)∗sin(β)+cos(α)∗sin(β)sin(α−β)=sin(α)∗cos(β)−cos(α)∗sin(β)
3.总结
∵ { c o s ( α + β ) = c o s ( α ) ∗ c o s ( β ) − s i n ( α ) ∗ s i n ( β ) s i n ( α + β ) = s i n ( α ) ∗ c o s ( β ) + c o s ( α ) ∗ s i n ( β ) c o s ( α − β ) = s i n ( α ) ∗ s i n ( β ) + c o s ( α ) ∗ s i n ( β ) s i n ( α − β ) = s i n ( α ) ∗ c o s ( β ) − c o s ( α ) ∗ s i n ( β ) ∵\begin{cases} cos(α+β)=cos(α)*cos(β)-sin(α)*sin(β) \\sin(α+β)=sin(α)*cos(β)+cos(α)*sin(β) \\cos(α-β)=sin(α)*sin(β)+cos(α)*sin(β) \\sin(α-β)=sin(α)*cos(β)-cos(α)*sin(β) \end{cases} ∵⎩ ⎨ ⎧cos(α+β)=cos(α)∗cos(β)−sin(α)∗sin(β)sin(α+β)=sin(α)∗cos(β)+cos(α)∗sin(β)cos(α−β)=sin(α)∗sin(β)+cos(α)∗sin(β)sin(α−β)=sin(α)∗cos(β)−cos(α)∗sin(β)
4.其他
为什么几何推理∠β和∠α不是钝角,根据诱导公式可将钝角化为锐角。所以只推导锐角和可以等价于推导任意角和
相关文章:

三角函数两角和差公式推导
一.几何推理 1.两角和公式 做一斜边为1的直角△ABC,任意旋转非 k Π , k N kΠ,kN kΠ,kN,补充如图,令 ∠ A B C ∠ α , ∠ C B F ∠ β ∠ABC∠α,∠CBF∠β ∠ABC∠α,∠CBF∠β ∴ ∠ D B F ∠ D B A ∠ α ∠ β 90 , ∠ D A …...
HarmonyOS page生命周期函数讲解
下面 我们又要看一个比较重要的点了 页面生命周期 页面组件有三个生命周期 onPageShow 页面显示时触发 onPageHide 页面隐藏时触发 onBackPress 页面返回时触发 这里 我们准备两个组件 首先是 index.ets 参考代码如下 import router from ohos.router Entry Component struc…...
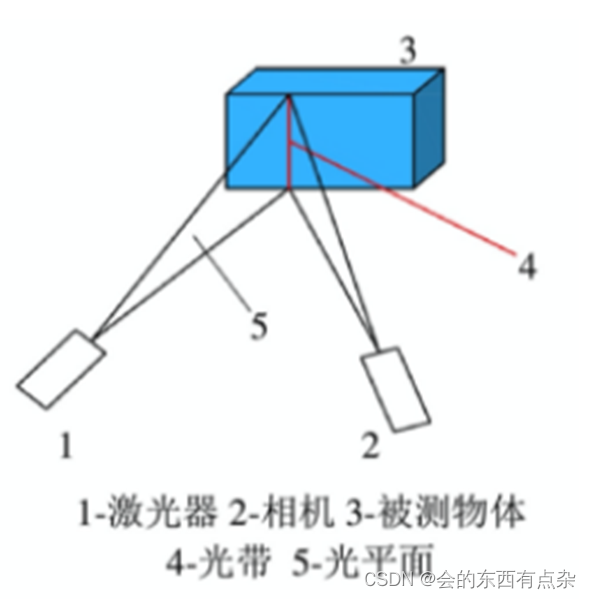
3D视觉-结构光测量-线结构光测量
概述 线结构光测量中,由激光器射出的激光光束透过柱面透镜扩束,再经过准直,产生一束片状光。这片光束像刀刃一样横切在待测物体表面,因此线结构光法又被成为光切法。线结构光测量常采用二维面阵 CCD 作为接受器件,因此…...
ssm基于web的马病管理系统设计与实现+jsp论文
摘 要 传统信息的管理大部分依赖于管理人员的手工登记与管理,然而,随着近些年信息技术的迅猛发展,让许多比较老套的信息管理模式进行了更新迭代,马病信息因为其管理内容繁杂,管理数量繁多导致手工进行处理不能满足广大…...
SaaS版Java基层健康卫生云HIS信息管理平台源码(springboot)
云his系统源码,系统采用主流成熟技术开发,B/S架构,软件结构简洁、代码规范易阅读,SaaS应用,全浏览器访问,前后端分离,多服务协同,服务可拆分,功能易扩展。多集团统一登录…...
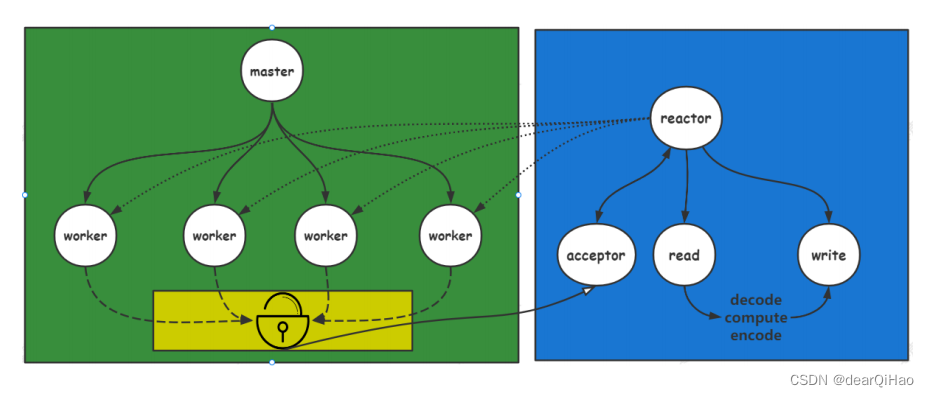
redis,memcached,nginx网络组件,网络编程——reactor的应用
目录 目标网络编程关注的问题连接的建立连接的断开消息的到达消息发送完毕 网络 IO 职责检测 IO检测 io剖析 操作 IO 阻塞IO 和 非阻塞IOIO 多路复用epoll结构以及接口 reactor编程连接建立连接断开数据到达数据发送完毕 reactor 应用:后续补充源码解析单 reacrtor多…...
)
【机电、机器人方向会议征稿|不限专业|见刊快】2024年机械、 图像与机器人国际会议(IACMIR 2024)
【机电、机器人方向会议征稿|不限专业|见刊快】2024年机械、 图像与机器人国际会议(IACMIR 2024) 2024 International Academic Conference on Machinery, Images, and Robotics 会议将聚焦“机械、成像和机器人”相关的最新研究领域,为国内…...

uniapp学习之路
uniapp 学习之路 1. 下载HBuilderX2. 下载uView初始框架3. 开始学习1.更改页面背景色,渐变色 1. 下载HBuilderX https://www.dcloud.io/hbuilderx.html?ivk_sa1024320u2. 下载uView初始框架 https://ext.dcloud.net.cn/plugin?id15933. 开始学习 1.更改页面背景…...
移动开发新的风口?Harmony4.0鸿蒙应用开发基础+实践案例
前段时间鸿蒙4.0引发了很多讨论,不少业内人士认为,鸿蒙将与iOS、安卓鼎足而三了。 事实上,从如今手机操作系统竞赛中不难看出,安卓与iOS的形态、功能逐渐趋同化,两大系统互相取长补短,综合性能等差距越来越…...
QT上位机开发(倒计时软件)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 倒计时软件是生活中经常遇到的一种场景。比如运动跑步,比如学校考试,比如论文答辩等等,只要有时间限制规定的地…...

2023 楚慧杯 --- Crypto wp
文章目录 初赛so large e 决赛JIGE 初赛 so large e 题目: from Crypto.Util.number import * from Crypto.PublicKey import RSA from flag import flag import randomm bytes_to_long(flag)p getPrime(512) q getPrime(512) n p*q e random.getrandbits(1…...
Python+OpenCV 零基础学习笔记(1-3):anaconda+vscode+jupyter环境配置
文章目录 前言相关链接环境配置:AnacondaPython配置OpenCVOpencv-contrib:Opencv扩展 Notebook:python代码笔记vscode配置配置AnacondaJupyter文件导出 前言 作为一个C# 上位机,我认为上位机的终点就是机器视觉运动控制。最近学了会Halcon发现机器视觉还…...
Spring Cloud Gateway 常见过滤器的基本使用
目录 1. 过滤器的作用 2. Spring Cloud Gateway 过滤器的类型 2.1 内置过滤器 2.1.1 AddResponseHeader 2.1.2 AddRequestHeader 2.1.3 PrefixPath 2.1.4 RequestRateLimiter 2.1.5 Retry 2.2 自定义过滤器 1. 过滤器的作用 过滤器通常用于拦截、处理或修改数据流和事…...

maven依赖无法传递问题排查
一、背景 在A模块中引入B模块,C服务引入A模块但是B模块没有传递进来。 二、排查 使用mvn clean install -Dmaven.test.skiptrue查看打包日志信息,通过搜索A模块名称,出现如下警告信息: [WARING] The POM for A:jar:0.0.1-SNAP…...

JVM钩子
JVM钩子 简介 在Java应用程序中,可以通过注册关闭钩子(Shutdown Hook)函数来实现在JVM关闭时执行特定的代码。关闭钩子是一种用于在JVM关闭时执行清理任务的机制,它允许开发者在JVM关闭之前执行一些必要的清理工作,如…...

linux cat命令增加-f显示文件名功能
在使用cat命令配合grep批量搜索文件内容时,我仅仅能知道是否搜索到,不知道是在哪个文件里找到的。比如cat ./src/*.c | grep full_write,在src目录下的所有.c文件里找full_write,能匹配到所有的full_write,但是不知道它们分别在哪些文件里。于…...

linux更改登录shell
从bash修改成python 在/etc/passwd下可以更改用户登录bash 例 root:x:0:0:root:/root:/bin/bash //更改bin/bash为/bin/python,就可以用root登录python页面了从python修改成bash 方法一 重启页面按e进入内核编辑模式linux16这行后添加:init/bin/…...
【JS】报错:Uncaught TypeError: Cannot read properties of null (reading ‘classList‘)
错误展示 今天写js代码的时候遇到报错: 源代码: <ul class"slider-indicator"><li class"active"></li><li></li><li></li><li></li><li></li><li><…...
kali2.0安装VMware Tools 和自定义改变分辨率
kali2.0安装VMware Tools 和自定义改变分辨率 VMware Tools 简介:VMware Tools安装:自定义改变分辨率:xrandr命令修改分辨率: 前言: 因为kali2.0比较老 所以需要手动安装 WMware Tools 进行复制粘贴操作! …...
redis中根据通配符删除key
redis中根据通配符删除key 我们是不是在redis中keys user:*可以获取所有key,但是 del user:*却不行这里我提供的命令主要是SCANSCAN 0 MATCH user:* COUNT 100使用lua保证原子性 SCAN参数描述 在示例中,COUNT 被设置为 100。这是一个防止一次性获取大…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...
