2023 楚慧杯 --- Crypto wp
文章目录
- 初赛
- so large e
- 决赛
- JIGE
初赛
so large e
题目:
from Crypto.Util.number import *
from Crypto.PublicKey import RSA
from flag import flag
import randomm = bytes_to_long(flag)p = getPrime(512)
q = getPrime(512)
n = p*q
e = random.getrandbits(1024)
assert size(e)==1024
phi = (p-1)*(q-1)
assert GCD(e,phi)==1
d = inverse(e,phi)
assert size(d)==269pub = (n, e)
PublicKey = RSA.construct(pub)
with open('pub.pem', 'wb') as f :f.write(PublicKey.exportKey())c = pow(m,e,n)
print('c =',c)print(long_to_bytes(pow(c,d,n)))#c = 6838759631922176040297411386959306230064807618456930982742841698524622016849807235726065272136043603027166249075560058232683230155346614429566511309977857815138004298815137913729662337535371277019856193898546849896085411001528569293727010020290576888205244471943227253000727727343731590226737192613447347860读取公钥得到n,e,
e = 113449247876071397911206070019495939088171696712182747502133063172021565345788627261740950665891922659340020397229619329204520999096535909867327960323598168596664323692312516466648588320607291284630435682282630745947689431909998401389566081966753438869725583665294310689820290368901166811028660086977458571233n = 116518679305515263290840706715579691213922169271634579327519562902613543582623449606741546472920401997930041388553141909069487589461948798111698856100819163407893673249162209631978914843896272256274862501461321020961958367098759183487116417487922645782638510876609728886007680825340200888068103951956139343723
根据代码,获悉
0.25 ≤ d n = 0.263 ≤ 0.292 0.25 \le \frac{d}{n} = 0.263\le0.292 0.25≤nd=0.263≤0.292
满足 Boneh and Durfee attack
直接套用模板,修改一下delta 和m即可
其中delta = 0.263,m = 5
exp:
#sage
from __future__ import print_function
import time############################################
# Config
##########################################"""
Setting debug to true will display more informations
about the lattice, the bounds, the vectors...
"""
debug = True"""
Setting strict to true will stop the algorithm (and
return (-1, -1)) if we don't have a correct
upperbound on the determinant. Note that this
doesn't necesseraly mean that no solutions
will be found since the theoretical upperbound is
usualy far away from actual results. That is why
you should probably use `strict = False`
"""
strict = False"""
This is experimental, but has provided remarkable results
so far. It tries to reduce the lattice as much as it can
while keeping its efficiency. I see no reason not to use
this option, but if things don't work, you should try
disabling it
"""
helpful_only = True
dimension_min = 7 # stop removing if lattice reaches that dimension############################################
# Functions
########################################### display stats on helpful vectors
def helpful_vectors(BB, modulus):nothelpful = 0for ii in range(BB.dimensions()[0]):if BB[ii,ii] >= modulus:nothelpful += 1print(nothelpful, "/", BB.dimensions()[0], " vectors are not helpful")# display matrix picture with 0 and X
def matrix_overview(BB, bound):for ii in range(BB.dimensions()[0]):a = ('%02d ' % ii)for jj in range(BB.dimensions()[1]):a += '0' if BB[ii,jj] == 0 else 'X'if BB.dimensions()[0] < 60:a += ' 'if BB[ii, ii] >= bound:a += '~'print(a)# tries to remove unhelpful vectors
# we start at current = n-1 (last vector)
def remove_unhelpful(BB, monomials, bound, current):# end of our recursive functionif current == -1 or BB.dimensions()[0] <= dimension_min:return BB# we start by checking from the endfor ii in range(current, -1, -1):# if it is unhelpful:if BB[ii, ii] >= bound:affected_vectors = 0affected_vector_index = 0# let's check if it affects other vectorsfor jj in range(ii + 1, BB.dimensions()[0]):# if another vector is affected:# we increase the countif BB[jj, ii] != 0:affected_vectors += 1affected_vector_index = jj# level:0# if no other vectors end up affected# we remove itif affected_vectors == 0:print("* removing unhelpful vector", ii)BB = BB.delete_columns([ii])BB = BB.delete_rows([ii])monomials.pop(ii)BB = remove_unhelpful(BB, monomials, bound, ii-1)return BB# level:1# if just one was affected we check# if it is affecting someone elseelif affected_vectors == 1:affected_deeper = Truefor kk in range(affected_vector_index + 1, BB.dimensions()[0]):# if it is affecting even one vector# we give up on this oneif BB[kk, affected_vector_index] != 0:affected_deeper = False# remove both it if no other vector was affected and# this helpful vector is not helpful enough# compared to our unhelpful oneif affected_deeper and abs(bound - BB[affected_vector_index, affected_vector_index]) < abs(bound - BB[ii, ii]):print("* removing unhelpful vectors", ii, "and", affected_vector_index)BB = BB.delete_columns([affected_vector_index, ii])BB = BB.delete_rows([affected_vector_index, ii])monomials.pop(affected_vector_index)monomials.pop(ii)BB = remove_unhelpful(BB, monomials, bound, ii-1)return BB# nothing happenedreturn BB"""
Returns:
* 0,0 if it fails
* -1,-1 if `strict=true`, and determinant doesn't bound
* x0,y0 the solutions of `pol`
"""
def boneh_durfee(pol, modulus, mm, tt, XX, YY):"""Boneh and Durfee revisited by Herrmann and Mayfinds a solution if:* d < N^delta* |x| < e^delta* |y| < e^0.5whenever delta < 1 - sqrt(2)/2 ~ 0.292"""# substitution (Herrman and May)PR.<u, x, y> = PolynomialRing(ZZ)Q = PR.quotient(x*y + 1 - u) # u = xy + 1polZ = Q(pol).lift()UU = XX*YY + 1# x-shiftsgg = []for kk in range(mm + 1):for ii in range(mm - kk + 1):xshift = x^ii * modulus^(mm - kk) * polZ(u, x, y)^kkgg.append(xshift)gg.sort()# x-shifts list of monomialsmonomials = []for polynomial in gg:for monomial in polynomial.monomials():if monomial not in monomials:monomials.append(monomial)monomials.sort()# y-shifts (selected by Herrman and May)for jj in range(1, tt + 1):for kk in range(floor(mm/tt) * jj, mm + 1):yshift = y^jj * polZ(u, x, y)^kk * modulus^(mm - kk)yshift = Q(yshift).lift()gg.append(yshift) # substitution# y-shifts list of monomialsfor jj in range(1, tt + 1):for kk in range(floor(mm/tt) * jj, mm + 1):monomials.append(u^kk * y^jj)# construct lattice Bnn = len(monomials)BB = Matrix(ZZ, nn)for ii in range(nn):BB[ii, 0] = gg[ii](0, 0, 0)for jj in range(1, ii + 1):if monomials[jj] in gg[ii].monomials():BB[ii, jj] = gg[ii].monomial_coefficient(monomials[jj]) * monomials[jj](UU,XX,YY)# Prototype to reduce the latticeif helpful_only:# automatically removeBB = remove_unhelpful(BB, monomials, modulus^mm, nn-1)# reset dimensionnn = BB.dimensions()[0]if nn == 0:print("failure")return 0,0# check if vectors are helpfulif debug:helpful_vectors(BB, modulus^mm)# check if determinant is correctly boundeddet = BB.det()bound = modulus^(mm*nn)if det >= bound:print("We do not have det < bound. Solutions might not be found.")print("Try with highers m and t.")if debug:diff = (log(det) - log(bound)) / log(2)print("size det(L) - size e^(m*n) = ", floor(diff))if strict:return -1, -1else:print("det(L) < e^(m*n) (good! If a solution exists < N^delta, it will be found)")# display the lattice basisif debug:matrix_overview(BB, modulus^mm)# LLLif debug:print("optimizing basis of the lattice via LLL, this can take a long time")BB = BB.LLL()if debug:print("LLL is done!")# transform vector i & j -> polynomials 1 & 2if debug:print("looking for independent vectors in the lattice")found_polynomials = Falsefor pol1_idx in range(nn - 1):for pol2_idx in range(pol1_idx + 1, nn):# for i and j, create the two polynomialsPR.<w,z> = PolynomialRing(ZZ)pol1 = pol2 = 0for jj in range(nn):pol1 += monomials[jj](w*z+1,w,z) * BB[pol1_idx, jj] / monomials[jj](UU,XX,YY)pol2 += monomials[jj](w*z+1,w,z) * BB[pol2_idx, jj] / monomials[jj](UU,XX,YY)# resultantPR.<q> = PolynomialRing(ZZ)rr = pol1.resultant(pol2)# are these good polynomials?if rr.is_zero() or rr.monomials() == [1]:continueelse:print("found them, using vectors", pol1_idx, "and", pol2_idx)found_polynomials = Truebreakif found_polynomials:breakif not found_polynomials:print("no independant vectors could be found. This should very rarely happen...")return 0, 0rr = rr(q, q)# solutionssoly = rr.roots()if len(soly) == 0:print("Your prediction (delta) is too small")return 0, 0soly = soly[0][0]ss = pol1(q, soly)solx = ss.roots()[0][0]#return solx, solydef example():############################################# How To Use This Script############################################ The problem to solve (edit the following values)## the modulusN = 116518679305515263290840706715579691213922169271634579327519562902613543582623449606741546472920401997930041388553141909069487589461948798111698856100819163407893673249162209631978914843896272256274862501461321020961958367098759183487116417487922645782638510876609728886007680825340200888068103951956139343723# the public exponente = 113449247876071397911206070019495939088171696712182747502133063172021565345788627261740950665891922659340020397229619329204520999096535909867327960323598168596664323692312516466648588320607291284630435682282630745947689431909998401389566081966753438869725583665294310689820290368901166811028660086977458571233# the hypothesis on the private exponent (the theoretical maximum is 0.292)delta = .263 # this means that d < N^delta## Lattice (tweak those values)## you should tweak this (after a first run), (e.g. increment it until a solution is found)m = 5 # size of the lattice (bigger the better/slower)# you need to be a lattice master to tweak theset = int((1-2*delta) * m) # optimization from Herrmann and MayX = 2*floor(N^delta) # this _might_ be too muchY = floor(N^(1/2)) # correct if p, q are ~ same size## Don't touch anything below## Problem put in equationP.<x,y> = PolynomialRing(ZZ)A = int((N+1)/2)pol = 1 + x * (A + y)## Find the solutions!## Checking boundsif debug:print("=== checking values ===")print("* delta:", delta)print("* delta < 0.292", delta < 0.292)print("* size of e:", int(log(e)/log(2)))print("* size of N:", int(log(N)/log(2)))print("* m:", m, ", t:", t)# boneh_durfeeif debug:print("=== running algorithm ===")start_time = time.time()solx, soly = boneh_durfee(pol, e, m, t, X, Y)# found a solution?if solx > 0:print("=== solution found ===")if False:print("x:", solx)print("y:", soly)d = int(pol(solx, soly) / e)print("private key found:", d)else:print("=== no solution was found ===")if debug:print(("=== %s seconds ===" % (time.time() - start_time)))if __name__ == "__main__":example()
计算得到d
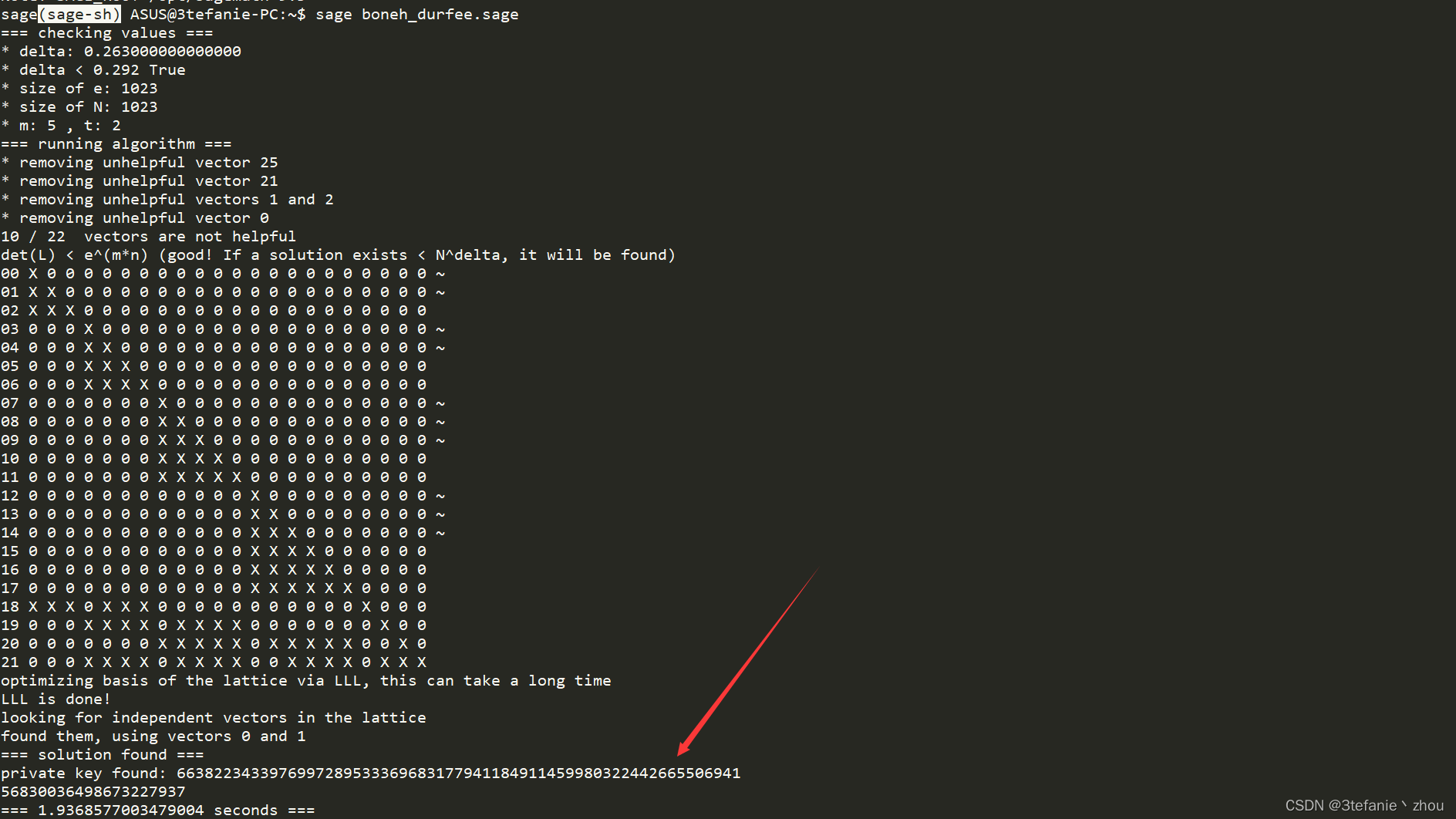
d = 663822343397699728953336968317794118491145998032244266550694156830036498673227937
最后RSA解密得到flag
#sage
c = 6838759631922176040297411386959306230064807618456930982742841698524622016849807235726065272136043603027166249075560058232683230155346614429566511309977857815138004298815137913729662337535371277019856193898546849896085411001528569293727010020290576888205244471943227253000727727343731590226737192613447347860
d = 663822343397699728953336968317794118491145998032244266550694156830036498673227937
n = 116518679305515263290840706715579691213922169271634579327519562902613543582623449606741546472920401997930041388553141909069487589461948798111698856100819163407893673249162209631978914843896272256274862501461321020961958367098759183487116417487922645782638510876609728886007680825340200888068103951956139343723
m = pow(c,d,n)
flag = bytes.fromhex(hex(m)[2:])
print(flag)
#DASCTF{6f4fadce-5378-d17f-3c2d-2e064db4af19}
决赛
JIGE
题目:
from gmpy2 import *
from hashlib import md5
from Crypto.Util.number import *
from sympy import *message=XXXXXX
flag = 'DASCTF{'+md5(message).hexdigest()+'}'
p = getPrime(256)
q = getPrime(256)
assert p > q
n = p * q
e = 0x10001 #65537
m = bytes_to_long(message)
c = pow(m, e, n)N = pow(p, 11) * q
d1 = getPrime(2000)
d2 = nextprime(d1 + getPrime(1000))
e1 = invert(d1, (pow(p, 10) * (p - 1) * (q - 1)))
e2 = invert(d2, (pow(p, 10) * (p - 1) * (q - 1)))print(f'c = {c}')
print(f'N = {N}')
print(f'e1 = {e1}')
print(f'e2 = {e2}')'''
c = 1206807362850301500412872994631699583002892289904471476523412128137773618173466272359196256671175708216503443050872032061782739223138420055283507423416014
N = 2769972268494457422626756881035680365791374852650158574600757210295514312723202376005992652087072745127197622954236101990451854162917559723722518981897097628959272185981219794883530767584841881112435651621934537571083225349949311621207409183741363444346000402562578450456645711882560128619242711698327278980081266684521150227771637075686195050487818614035674633610096137625035790732645845723462391311298302637686542232835581871746884130013070996968184596449672622781116306181302392813217024411730226953994648038878074679828551669837254152265441513617958229372943240214088399450834487541147274643124286983672414825675492669859487862886608989862491581277404219285561282275675102529309186029976081969486912697417132568798720377963032348920342675126756050513673101405664709184620104181654397512121633023592966498206439167017063802120497727043888826589401745202319033829767714724756122673441156732069183201569766204472097988081541
e1 = 2019789551019093124420297272384567741634310853673511749178611164072776295834811119450621861426097251426338761387400947669712980885171825246712129400923345045714062211913328737569990247227840399725205366257333392335095407072561983345874628219982166479392648454069496646733709717240335264301129096508037181465890164627276692696540046415077712807666335629672257696160380799064676194674815656129599632459744438651570247278542393673849808278202966914757001771181720554604666343205509941102540930522715083963211556704973593626830060515529201025992233193710032293801887064920491994892731059564016729184073592209700547810374523193198684464611594086849851216947777536116800375704509948170375971236541467019409313469504630988967011023280553412399918851721362010464793913169072750314771104456079550196999871385309352503595586614818585704007635869697001268017638044593755012233245211072647051603150602669710674109645174749520576295708163
e2 = 1583703592049684873685114339953437401553059969077370065722292597953883761416746559834892164581234164438330080827740800363198430396478731634782581595240544469072569584848085012992026166904750154014378216852052182115039653650262042887676171319128137818446568464062868113062233139620367603439600244722942659267734053620937005194939432606278744697609503707934576549002757520737074102321078418822923889399221127593632747782118004212766847803779185975309956970980280169387201657554918144244843463689062591309308003163435148432749203807727111886042271473627935482161154494976464303547129663586810973936239964669196142557977332701367619795730332662446023712262922190841226239360097490311533265953167562594634954870494720064733019963379137130620318351648747992348207245430288065933286523588168735037017481803349125024025183996822657547245651094947702268545834292593852409172743667084611813423926836813703374530071303810930647531379459
'''
考察论文New attacks on RSA with Moduli N = p^rq

根据论文,可以构建如下多项式
e 1 e 2 ( d 1 − d 2 ) ≡ e 2 − e 1 m o d ϕ ( n ) e_1e_2(d_1-d_2) \equiv e_2-e_1 \space mod \space \phi(n) e1e2(d1−d2)≡e2−e1 mod ϕ(n)
因为 ϕ ( n ) = p r − 1 ( p − 1 ) ( q − 1 ) \phi(n) = p^{r-1}(p-1)(q-1) ϕ(n)=pr−1(p−1)(q−1),所以上式子可以变为
e 1 e 2 x − ( e 2 − e 1 ) ≡ 0 m o d p r − 1 e_1e_2x-(e_2-e_1) \equiv0 \space mod \space p^{r-1} e1e2x−(e2−e1)≡0 mod pr−1
当 ∣ d 1 − d 2 ∣ < n r ( r − 1 ) ( r + 1 ) 2 |d_1-d_2|<n^\frac{r(r-1)}{(r+1)^2} ∣d1−d2∣<n(r+1)2r(r−1)时,在多项式时间内可解
copper出x,也就是d1-d2
计算 g c d ( e 1 e 2 x − ( e 2 − e 1 ) , n ) = g c d ( y × p r − 1 ( p − 1 ) ( q − 1 ) , p r q ) = g gcd(e_1e_2x-(e_2-e_1),n) = gcd(y\times p^{r-1}(p-1)(q-1),p^rq) = g gcd(e1e2x−(e2−e1),n)=gcd(y×pr−1(p−1)(q−1),prq)=g
p的值按如下情况取
w h e n g = p r − 1 , p = g 1 r − 1 ( 1 ) when \space g = p^{r-1},p = g^{\frac{1}{r-1}} \hspace {2cm} (1) when g=pr−1,p=gr−11(1)
w h e n g = p r , p = g 1 r ( 2 ) when \space g = p^{r},p = g^{\frac{1}{r}} \hspace {2.5cm} (2) when g=pr,p=gr1(2)
w h e n g = p r − 1 q , p = n g ( 3 ) when \space g = p^{r-1}q,p = \frac{n}{g} \hspace {2.1cm} (3) when g=pr−1q,p=gn(3)
在本题中,我们得到的g为2560bit,p为256bit,那么 g = p 11 − 1 = p 10 g = p^{11-1} = p^{10} g=p11−1=p10
直接开10次方得到p,进而q = n//p^11,最后RSA解密再计算明文的md5摘要即可获得flag
exp:
#sage
import gmpy2
from hashlib import *c = 1206807362850301500412872994631699583002892289904471476523412128137773618173466272359196256671175708216503443050872032061782739223138420055283507423416014
n = 2769972268494457422626756881035680365791374852650158574600757210295514312723202376005992652087072745127197622954236101990451854162917559723722518981897097628959272185981219794883530767584841881112435651621934537571083225349949311621207409183741363444346000402562578450456645711882560128619242711698327278980081266684521150227771637075686195050487818614035674633610096137625035790732645845723462391311298302637686542232835581871746884130013070996968184596449672622781116306181302392813217024411730226953994648038878074679828551669837254152265441513617958229372943240214088399450834487541147274643124286983672414825675492669859487862886608989862491581277404219285561282275675102529309186029976081969486912697417132568798720377963032348920342675126756050513673101405664709184620104181654397512121633023592966498206439167017063802120497727043888826589401745202319033829767714724756122673441156732069183201569766204472097988081541
e1 = 2019789551019093124420297272384567741634310853673511749178611164072776295834811119450621861426097251426338761387400947669712980885171825246712129400923345045714062211913328737569990247227840399725205366257333392335095407072561983345874628219982166479392648454069496646733709717240335264301129096508037181465890164627276692696540046415077712807666335629672257696160380799064676194674815656129599632459744438651570247278542393673849808278202966914757001771181720554604666343205509941102540930522715083963211556704973593626830060515529201025992233193710032293801887064920491994892731059564016729184073592209700547810374523193198684464611594086849851216947777536116800375704509948170375971236541467019409313469504630988967011023280553412399918851721362010464793913169072750314771104456079550196999871385309352503595586614818585704007635869697001268017638044593755012233245211072647051603150602669710674109645174749520576295708163
e2 = 1583703592049684873685114339953437401553059969077370065722292597953883761416746559834892164581234164438330080827740800363198430396478731634782581595240544469072569584848085012992026166904750154014378216852052182115039653650262042887676171319128137818446568464062868113062233139620367603439600244722942659267734053620937005194939432606278744697609503707934576549002757520737074102321078418822923889399221127593632747782118004212766847803779185975309956970980280169387201657554918144244843463689062591309308003163435148432749203807727111886042271473627935482161154494976464303547129663586810973936239964669196142557977332701367619795730332662446023712262922190841226239360097490311533265953167562594634954870494720064733019963379137130620318351648747992348207245430288065933286523588168735037017481803349125024025183996822657547245651094947702268545834292593852409172743667084611813423926836813703374530071303810930647531379459
e = 65537
a = e1 * e2
b = (e2 - e1)
R.<x> = PolynomialRing(Zmod(n))
f = a*x - b
f = f.monic()
res = f.small_roots(2^2000,beta = 0.4)
ans = int(res[0])
tmp = GCD(a*ans - b,n)
p = gmpy2.iroot(tmp,10)[0]
q = n//(p**11)
phi = (p-1)*(q-1)
d = inverse_mod(e,phi)
m = pow(c,d,p*q)
plain = bytes.fromhex(hex(m)[2:])
#YOU MUST BE A XIAOHEIZI
flag = 'DASCTF{'+md5(plain).hexdigest()+'}'
print(flag)
#DASCTF{4ed94d288633e880f9d8a53039247805}
【世上伤病千百种,情伤病入膏肓,心病无药可救。】
相关文章:

2023 楚慧杯 --- Crypto wp
文章目录 初赛so large e 决赛JIGE 初赛 so large e 题目: from Crypto.Util.number import * from Crypto.PublicKey import RSA from flag import flag import randomm bytes_to_long(flag)p getPrime(512) q getPrime(512) n p*q e random.getrandbits(1…...
Python+OpenCV 零基础学习笔记(1-3):anaconda+vscode+jupyter环境配置
文章目录 前言相关链接环境配置:AnacondaPython配置OpenCVOpencv-contrib:Opencv扩展 Notebook:python代码笔记vscode配置配置AnacondaJupyter文件导出 前言 作为一个C# 上位机,我认为上位机的终点就是机器视觉运动控制。最近学了会Halcon发现机器视觉还…...
Spring Cloud Gateway 常见过滤器的基本使用
目录 1. 过滤器的作用 2. Spring Cloud Gateway 过滤器的类型 2.1 内置过滤器 2.1.1 AddResponseHeader 2.1.2 AddRequestHeader 2.1.3 PrefixPath 2.1.4 RequestRateLimiter 2.1.5 Retry 2.2 自定义过滤器 1. 过滤器的作用 过滤器通常用于拦截、处理或修改数据流和事…...

maven依赖无法传递问题排查
一、背景 在A模块中引入B模块,C服务引入A模块但是B模块没有传递进来。 二、排查 使用mvn clean install -Dmaven.test.skiptrue查看打包日志信息,通过搜索A模块名称,出现如下警告信息: [WARING] The POM for A:jar:0.0.1-SNAP…...

JVM钩子
JVM钩子 简介 在Java应用程序中,可以通过注册关闭钩子(Shutdown Hook)函数来实现在JVM关闭时执行特定的代码。关闭钩子是一种用于在JVM关闭时执行清理任务的机制,它允许开发者在JVM关闭之前执行一些必要的清理工作,如…...

linux cat命令增加-f显示文件名功能
在使用cat命令配合grep批量搜索文件内容时,我仅仅能知道是否搜索到,不知道是在哪个文件里找到的。比如cat ./src/*.c | grep full_write,在src目录下的所有.c文件里找full_write,能匹配到所有的full_write,但是不知道它们分别在哪些文件里。于…...

linux更改登录shell
从bash修改成python 在/etc/passwd下可以更改用户登录bash 例 root:x:0:0:root:/root:/bin/bash //更改bin/bash为/bin/python,就可以用root登录python页面了从python修改成bash 方法一 重启页面按e进入内核编辑模式linux16这行后添加:init/bin/…...
【JS】报错:Uncaught TypeError: Cannot read properties of null (reading ‘classList‘)
错误展示 今天写js代码的时候遇到报错: 源代码: <ul class"slider-indicator"><li class"active"></li><li></li><li></li><li></li><li></li><li><…...
kali2.0安装VMware Tools 和自定义改变分辨率
kali2.0安装VMware Tools 和自定义改变分辨率 VMware Tools 简介:VMware Tools安装:自定义改变分辨率:xrandr命令修改分辨率: 前言: 因为kali2.0比较老 所以需要手动安装 WMware Tools 进行复制粘贴操作! …...
redis中根据通配符删除key
redis中根据通配符删除key 我们是不是在redis中keys user:*可以获取所有key,但是 del user:*却不行这里我提供的命令主要是SCANSCAN 0 MATCH user:* COUNT 100使用lua保证原子性 SCAN参数描述 在示例中,COUNT 被设置为 100。这是一个防止一次性获取大…...
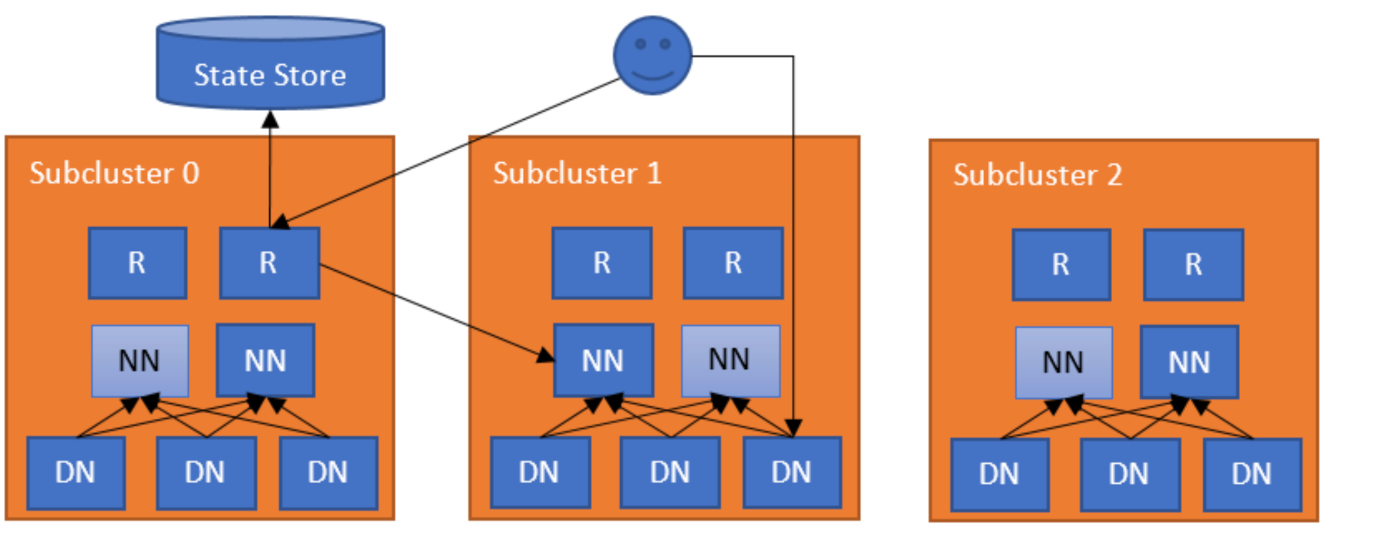
【HDFS联邦(2)】HDFS Router-based Federation官网解读:HDFSRouterFederation的架构、各组件基本原理
文章目录 一. 介绍二、HDFS Router-based Federation 架构1. 示例说明2. Router2.1. Federated interface2.2. Router heartbeat2.3. NameNode heartbeat2.4. Availability and fault toleranceInterfaces 3. Quota management4. State Store 三、部署 ing 本文主要参考官网&am…...

【头歌实训】Spark 完全分布式的安装和部署
文章目录 第1关: Standalone 分布式集群搭建任务描述相关知识课程视频Spark分布式安装模式示例集群信息配置免密登录准备Spark安装包配置环境变量修改 spark-env.sh 配置文件修改 slaves 文件分发安装包启动spark验证安装 编程要求测试说明答案代码报错问题基本过程…...
Leetcode—86.分隔链表【中等】
2023每日刷题(六十九) Leetcode—86.分隔链表 实现代码 /*** Definition for singly-linked list.* struct ListNode {* int val;* struct ListNode *next;* };*/ struct ListNode* partition(struct ListNode* head, int x) {struct ListNode…...

淘宝/天猫商品API:实时数据获取与安全隐私保护的指南
一、引言 随着电子商务的快速发展,淘宝/天猫等电商平台已成为商家和消费者的重要交易场所。对于电商企业而言,实时掌握店铺商品的销售情况、库存状态等信息至关重要。然而,手动管理和更新商品信息既费时又费力。因此,淘宝/天猫提…...
使用 SSH 方式实现 Git 远程连接GitHub
git是目前世界上最先进的分布式版本控制系统,相比于SVN,分布式版本系统的最大好处之一是在本地工作完全不需要考虑远程库的存在,也就是有没有联网都可以正常工作!当有网络的时候,再把本地提交推送一下就完成了同步&…...

Centos7部署Keepalived+lvs服务
IP规划: 服务器IP地址主服务器20.0.0.22/24从服务器20.0.0.24/24Web-120.0.0.26/24Web-220.0.0.27/24 一、主服务器安装部署keepalivedlvs服务 1、调整/proc响应参数 关闭Linux内核的重定向参数,因为LVS负载服务器和两个页面服务器需要共用一个VIP地…...
12/31
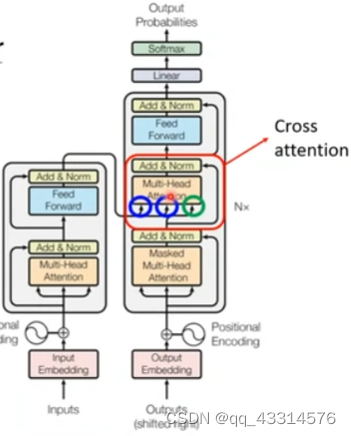
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 摘要Abstract文献阅读:用于密集预测的多路径视觉Transformer1、研究背景2、方法提出3、相关方法3.1、Vision Transformers for dense predictions3.2、C…...
python使用openpyxl为excel模版填充数据,生成多个Sheet页面
目标:希望根据一个给定的excel模版,生成多个Sheet页面,比如模版: 示例程序 import openpyxlexcel_workbook openpyxl.load_workbook("模版.xlsx") for _i in range(3): # 比如填充3个页面# 复制模版sheet页&#x…...
基于ssm的4S店预约保养系统开发+vue论文
目 录 目 录 I 摘 要 III ABSTRACT IV 1 绪论 1 1.1 课题背景 1 1.2 研究现状 1 1.3 研究内容 2 2 系统开发环境 3 2.1 vue技术 3 2.2 JAVA技术 3 2.3 MYSQL数据库 3 2.4 B/S结构 4 2.5 SSM框架技术 4 3 系统分析 5 3.1 可行性分析 5 3.1.1 技术可行性 5 3.1.2 操作可行性 5 3…...
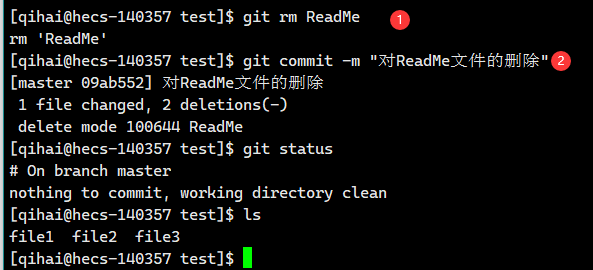
【Git】Git的基本操作
前言 Git是当前最主流的版本管理器,它可以控制电脑上的所有格式的文件。 它对于开发人员,可以管理项目中的源代码文档。(可以记录不同提交的修改细节,并且任意跳转版本) 本篇博客基于最近对Git的学习,简单介…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...

leetcode73-矩阵置零
leetcode 73 思路 记录 0 元素的位置:遍历整个矩阵,找出所有值为 0 的元素,并将它们的坐标记录在数组zeroPosition中置零操作:遍历记录的所有 0 元素位置,将每个位置对应的行和列的所有元素置为 0 具体步骤 初始化…...
