模式识别与机器学习-SVM(带软间隔的支持向量机)
SVM(带软间隔的支持向量机)
- 软间隔思想的由来
- 软间隔的引入
谨以此博客作为复习期间的记录。
软间隔思想的由来
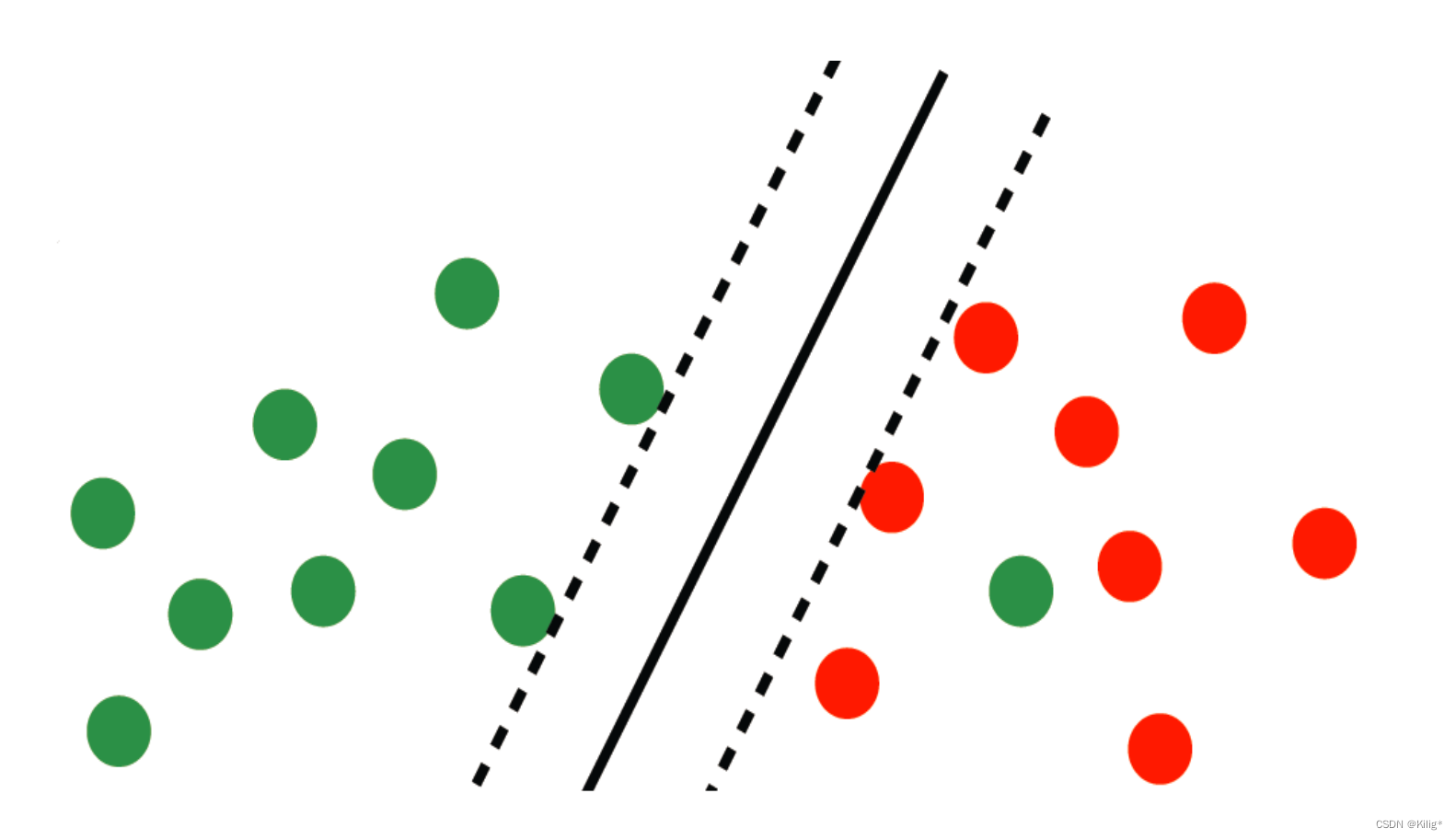
在上一篇博客中,回顾了线性可分的支持向量机,但在实际情况中,很少有完全线性可分的情况,大部分线性可分的情况都是整体线性可分,个别样本点无法线性分割开。因此就要避免这极个别样本点对分割平面产生的影响。
线性可分支持向量机
软间隔的引入
在分类过程中,允许极个别数据点“越界”,如何在目标函数中体现这一点呢?
软间隔支持向量机(Soft Margin Support Vector Machine)的数学形式可以通过修改支持向量机(SVM)的优化目标函数和约束条件来实现。软间隔允许一些数据点越界,引入了松弛变量来处理这些点。
首先,我们考虑软间隔的目标函数和约束条件:
-
目标函数:
最小化目标函数,同时考虑间隔的最大化和误分类点的惩罚,即:
min w , b , ξ 1 2 ∥ w ∥ 2 + C ∑ i = 1 N ξ i \min_{\mathbf{w}, b, \boldsymbol{\xi}} \frac{1}{2}\|\mathbf{w}\|^2 + C \sum_{i=1}^{N} \xi_i w,b,ξmin21∥w∥2+Ci=1∑Nξi
这里 w \mathbf{w} w 是超平面的法向量, b b b 是截距, ξ \boldsymbol{\xi} ξ 是松弛变量, C > 0 C > 0 C>0 是一个超参数,用于控制对误分类点的惩罚程度。 -
约束条件:
考虑函数间隔大于等于 1 的约束条件,以及松弛变量 ξ \boldsymbol{\xi} ξ 的非负性约束:
y i ( w ⋅ x i + b ) ≥ 1 − ξ i , i = 1 , 2 , … , N ξ i ≥ 0 , i = 1 , 2 , … , N \begin{align*} & y_i(\mathbf{w} \cdot \mathbf{x}_i + b) \geq 1 - \xi_i, \quad i = 1, 2, \dots, N \\ & \xi_i \geq 0, \quad i = 1, 2, \dots, N \end{align*} yi(w⋅xi+b)≥1−ξi,i=1,2,…,Nξi≥0,i=1,2,…,N
线性支持向量机学习算法
输入: 训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } T=\left\{\left(x_1, y_1\right),\left(x_2, y_2\right), \cdots,\left(x_N, y_N\right)\right\} T={(x1,y1),(x2,y2),⋯,(xN,yN)}, 其中, x i ∈ X = R n , y i ∈ x_i \in \mathcal{X}=\mathbf{R}^n, y_i \in xi∈X=Rn,yi∈ Y = { − 1 , + 1 } , i = 1 , 2 , ⋯ , N \mathcal{Y}=\{-1,+1\}, \quad i=1,2, \cdots, N Y={−1,+1},i=1,2,⋯,N;
输出: 分离超平面和分类决策函数.
(1) 选择惩罚参数 C > 0 C>0 C>0, 构造并求解凸二次规划问题
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i s.t. ∑ i = 1 N α i y i = 0 0 ⩽ α i ⩽ C , i = 1 , 2 , ⋯ , N \begin{aligned} \min _\alpha & \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j\left(x_i \cdot x_j\right)-\sum_{i=1}^N \alpha_i \\ \text { s.t. } & \sum_{i=1}^N \alpha_i y_i=0 \\ & 0 \leqslant \alpha_i \leqslant C, \quad i=1,2, \cdots, N \end{aligned} αmin s.t. 21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−i=1∑Nαii=1∑Nαiyi=00⩽αi⩽C,i=1,2,⋯,N
求得最优解 α ∗ = ( α 1 ∗ , α 2 ∗ , ⋯ , α N ∗ ) T \alpha^*=\left(\alpha_1{ }^*, \alpha_2{ }^*, \cdots, \alpha_N{ }^*\right)^{\mathrm{T}} α∗=(α1∗,α2∗,⋯,αN∗)T.
(2) 计算 w ∗ = ∑ i = 1 N α i ∗ y i x i w^*=\sum_{i=1}^N \alpha_i^* y_i x_i w∗=∑i=1Nαi∗yixi
选择 α ∗ \alpha^* α∗ 的一个分量 α j ∗ \alpha_j{ }^* αj∗ 适合条件 0 < α j ∗ < C 0<\alpha_j^*<C 0<αj∗<C, 计算
b ∗ = y j − ∑ i = 1 N y i α i ∗ ( x i ⋅ x j ) b^*=y_j-\sum_{i=1}^N y_i \alpha_i^*\left(x_i \cdot x_j\right) b∗=yj−i=1∑Nyiαi∗(xi⋅xj)
(3) 求得分离超平面
w ∗ ⋅ x + b ∗ = 0 w^* \cdot x+b^*=0 w∗⋅x+b∗=0
分类决策函数:
f ( x ) = sign ( w ∗ ⋅ x + b ∗ ) f(x)=\operatorname{sign}\left(w^* \cdot x+b^*\right) f(x)=sign(w∗⋅x+b∗)
相关文章:

模式识别与机器学习-SVM(带软间隔的支持向量机)
SVM(带软间隔的支持向量机) 软间隔思想的由来软间隔的引入 谨以此博客作为复习期间的记录。 软间隔思想的由来 在上一篇博客中,回顾了线性可分的支持向量机,但在实际情况中,很少有完全线性可分的情况,大部分线性可分…...

CentOS 7 firewalld+ipset+定时任务防御ssh暴力破解——筑梦之路
对于暴露在公网上的linux服务器,很容易被暴力破解登陆,为了增强服务器的安全性,因此对于ssh安全加固是很有必要的,这里主要介绍centos7 系统如何使用ipsetfirewalld定时任务来对ssh服务进行安全加固。 定义firewalld ipset fire…...

ElasticSearch的RestClient结合Sniffer提高可用性
一、背景 由于要安装分词器插件,所以需要重启ElasticSearch集群以使得新安装的插件生效 但是在重启集群的过程中,服务端代码却出现了大量错误,如下所示 java.net.ConnectException: Connection refused at org.elasticsearch.client.R…...

【网络面试(2)】DNS原理-域名和IP地址的查询转换
从上一篇博客我们得知浏览器是如何生成了HTTP消息了,但是浏览器作为应用程序,是不具备向网络中发送请求的能力,而是需要委托给操作系统的内核协议栈来发送请求。在委托协议栈之前,浏览器还要做的一件事情就是将域名转换为IP地址。…...

【PHP】函数array_intersect、array_diff:从数组中取出、去除指定的几个键值
1.从数组中取出 :array_intersect 要从数组中取出指定的几个键值,可以使用 array_intersect_key 函数。以下是一个示例: $array [name > John,age > 30,email > johnexample.com,city > New York ];$keys [name, email];$resu…...

【华为机试】2023年真题B卷(python)-冠亚军排名-奖牌榜排名
一、题目 题目描述: 2012伦敦奥运会即将到来,大家都非常关注奖牌榜的情况,现在我们假设奖牌榜的排名规则如下. 1.首先gold medal数量多的排在前面 2.其次silver medal数量多的排在前面 3.然后bronze medal数量多的排在前面 4.若以上三个条…...

MyBatisPlus之逻辑删除
系列文章目录 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 MyBatisPlus之逻辑删除 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 系列文章目录前言一、什么是逻辑删…...
在macOS中搭建.NET MAUI开发环境
文章目录 准备安装扩展安装 .NET安装工作负载安装 Xcode 命令行工具调试安卓应用安装 JDK安装 Android SDK 安装 Android 模拟器安装模拟器安装镜像创建虚拟机 同意许可条款创建 MAUI 项目调试 MAUI 应用切换调试目标 参考资料 准备 一台 macOS Monterey 以上的电脑安装 XCode…...
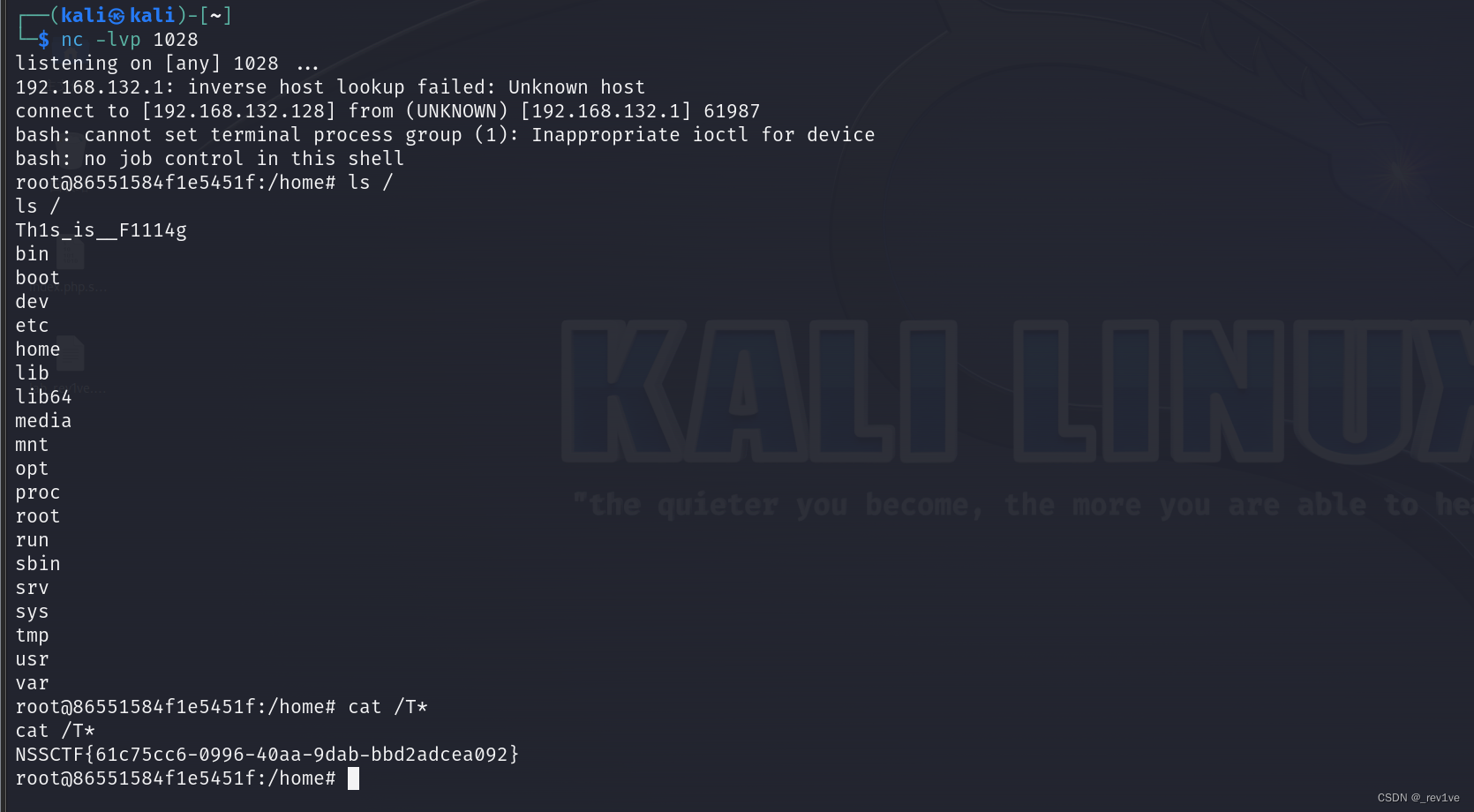
[NCTF 2022]calc
[NCTF 2022]calc 考点:python环境变量注入 打开题目,F12有hint 访问一下得到源码 app.route("/calc",methods[GET]) def calc():ip request.remote_addrnum request.values.get("num")log "echo {0} {1} {2}> ./tmp/log…...
【pandas_不重复项计数】
听说WPS没有非重复项计数的功能,而office需要添加到数据模型之后,才可以使用该功能。而用pandas,既可以对重复项计数,又可以对非重复项计数。 # 使用提醒: # 1. xbot包提供软件自动化、数据表格、Excel、日志、AI等功能 # 2. pack…...
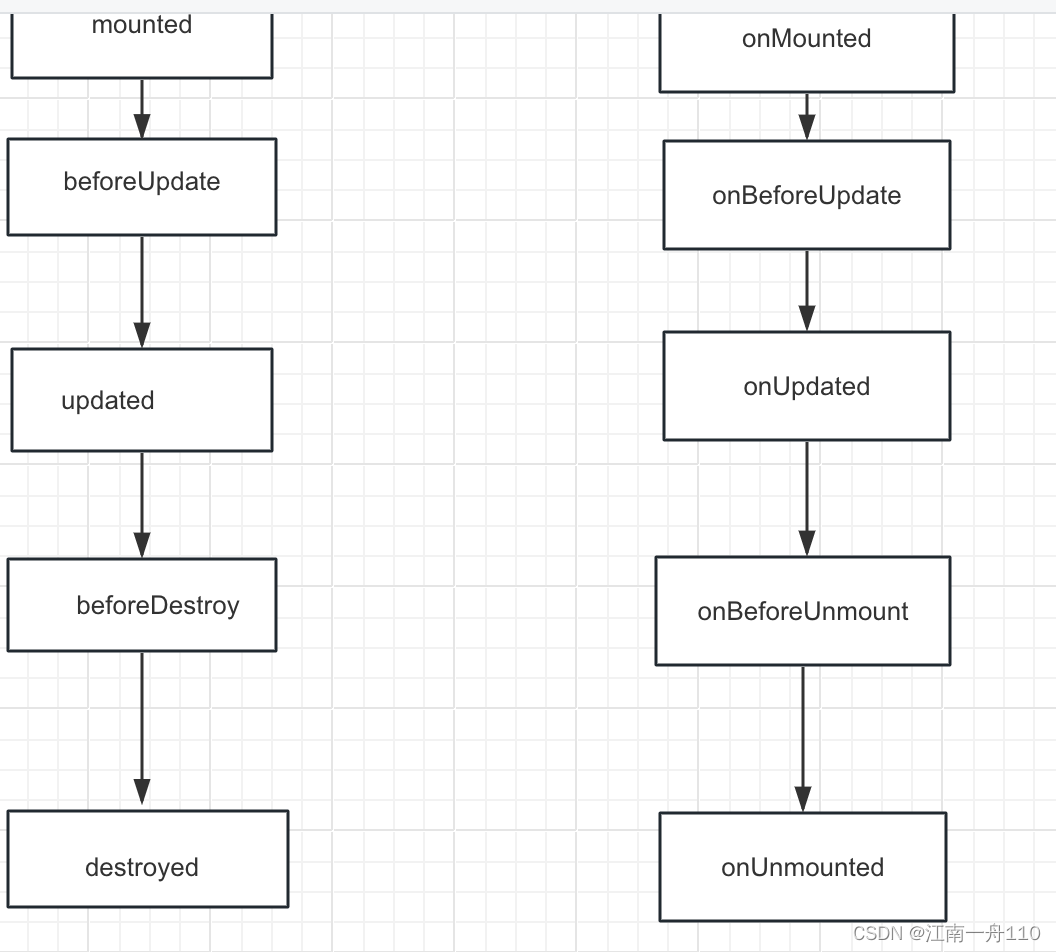
菜鸟学习vue3笔记-vue hooks初体验
import { ref } from "vue"; export default function () {let a1 ref(1);let a2 ref(5);let c ref(0);function add() {a1.value;a2.value;}return {add,a1,a2,c,}; }<template><div><p>第一个数字{{ a1 }}</p><p>第二个数字{{ a2…...

81 使用DFS和BFS解机器人的运动范围
问题描述:地上有一个m行n列的方格,从坐标[0,0]到坐标[m-1,n-1].一个机器人从坐标[0,0]的格子开始移动,他每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。 public int numB…...
vue-springboot基于JavaWeb的家装一体化商城平台guptn
针对用户需求开发与设计,该技术尤其在各行业领域发挥了巨大的作用,有效地促进了家装一体化的发展。然而,由于用户量和需求量的增加,信息过载等问题暴露出来,为改善传统线下管理中的不足,本文将提出一套基于…...

.NET进阶篇06-async异步、thread多线程2
知识须要不断积累、总结和沉淀,思考和写做是成长的催化剂web 内容目录 1、线程Thread 一、生命周期 二、后台线程 三、静态方法 1.线程本地存储 2.内存栅栏 四、返回值 2、线程池ThreadPool 一、工做队列 二、工做线程和IO线程 三、和Thread区别 四、定时器 1、线…...

java 方法
方法: 什么是方法,有什么用? 方法(英语单词:method)是可以完成某个特定功能的并且可以被重复利用的代码片段。 在 C 语言中,方法被称为“函数”。在 java 中不叫函数,叫做方法。 方法…...
HarmonyOS 组件通用属性之通用事件 文档参数讲解(点击事件)
我们组件中 会有很多通用的信息和方法 那么 首先 我们看通用事件 通用事件中 最常用的就是我们的点击事件 比如说 我们之前常写的 组件.onClick(()>{//事件逻辑 })但是 我们之前 都没有用它接参数 我们可以这样 Button("跳转").onClick((ewat: ClickEvent)>…...

毕业设计之开题报告
终于轮到我来写开题报告了,呃呃呃呃呃,目前有点难产了。想做的东西是关于区块链的后端设计实现,但是因为是完全原创之前没有类似的项目能去参考,所以其实有点慌的。 框架梳理 这是我们开题报告的要求: 包括题目研究的…...

【数据结构】详细剖析线性表
顺序表与链表的比较 导言一、线性表二、线性表的存储结构三、顺序表和链表的相同点四、顺序表与链表之间的差异五、存储结构的选择六、静态顺序表的基本操作七、无头结点单链表的基本操作结语 导言 大家好,很高兴又和大家见面啦!!࿰…...

通过数字证书对PDF电子文件进行数字签名/盖章
以下代码详细说明如何使用数字证书对PDF电子文件进行数字签名/盖章。PDF文件签署主要传递PDF文件,数字证书信息,签章图片3个信息。代码中需要的文件、数字证书、签章图片可访问开放签电子签章开源系统详细了解系统的实现与效果。也可通过gitee开源社区下…...

2007~2016 年税调经纬度及其所处的省市区县乡镇数据
之前给大家分享过一份税调企业经纬度及其所处的省市区县数据: 2007~2016 年税调企业地理信息数据(含经纬度及其所处的省市区县):https://rstata.duanshu.com/#/course/76d38022cd004b09b2aa09647936beb0 最近有培训班的小伙伴提出是否能根据税调企业经纬度来判断其所属的乡…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
